基于轨迹预测的高超声速飞行器拦截中/末制导研究
李庚泽,魏喜庆,王社阳
(1.中国人民解放军92941部队,辽宁 葫芦岛 125000; 2.上海机电工程研究所,上海 201109)
基于轨迹预测的高超声速飞行器拦截中/末制导研究
李庚泽1,魏喜庆2,王社阳2
(1.中国人民解放军92941部队,辽宁 葫芦岛 125000; 2.上海机电工程研究所,上海 201109)
针对因高超声速飞行器全程飞行速度快且具较强的机动能力,导致中末制导需用过载超出可用过载,采用传统制导律难以满足拦截需求的问题,对一种基于虚拟目标的高超声速飞行器轨迹拦截方法进行了研究。基于目标Singer运动学模型和量测模型,用扩展卡尔曼滤波(EKF)估计目标运动信息,将预测命中时刻目标运动轨迹作为虚拟目标点,考虑拦截交会角约束,采用针对虚拟目标的中制导拦截策略,在末制导段采用比例修正制导。通过随距离可变的末制导过渡段指令,以避免中末制导弹道交班的过载抖动。仿真结果表明:基于虚拟目标点高超声速目标拦截能有效减小末端弹目交会角同时降低需用过载。为降低中制导误差,可在拦截过程中实时更新一次虚拟目标的预测结果。该法可用于高超声速飞行器拦截,以及其他大机动目标的轨迹预测和拦截。
高超声速; 拦截; 轨迹预测; 制导律; Singer模型; 扩展卡尔曼滤波; 虚拟目标; 过载
0 引言
高超声速飞行器飞行速度快,严重压缩预警系统反应时间,对中/近程防空武器的拦截能力提出了较高的要求[1-3]。拦截弹的速度一般小于高超声速目标,不再具速度优势,因此采用传统的攻击方式难以保证拦截的精度。对高速大机动目标的拦截通常采用迎头拦截策略,其基本原理是拦截器接近目标时以目标速度矢量的反方向正面迎击目标,便于导引头截获和稳定跟踪目标,使拦截器能以较低的速度拦截高速目标;较小交会角能有效降低末制导对拦截器的过载需求。为保证导弹上视场受限的导引头能探测和监视到目标,文献[4]设计了一种前置角度约束的最优中制导律。针对反导导弹,文献[5]设计了一种基于T-S模糊方法和滑模控制的中制导律,该制导律能引导反导导弹以指定的姿态到达指定的位置,且对不确定性和外界干扰具鲁棒性。文献[6]基于修正的PID控制方法,研究了一种用于拦截快速机动目标的改进型PN导引律。文献[7]提出了考虑和不考虑攻击角约束的滑模面的统一设计方法,设计了一种基于不确定性和扰动估计器的二阶滑模导引律。文献[8]综合积分滑模控制(ISMC)和状态相关黎卡提方程(SDRE)设计了一种鲁棒导引律。文献[9]在导弹沿视线方向可控假设下,基于局部滑模设计了一种三维非线性导引律。文献[10]针对随机机动目标,应用线性二次型随机高斯最优控制理论和随机输入描述函数设计了一种导弹过载约束的随机最优导引律。文献[11]针对临近空间高超声速飞行器,基于结构随机跳变系统多模型理论和最优控制理论,设计了一种新型最优导引律。
为有效降低需用过载进而实现对高超声速飞行器的拦截,基于轨迹预测和角度约束本文对一种全新拦截策略进行了研究。其中设计的拦截策略包括如下三个步骤:用当前时刻的雷达观测值对系统的状态量进行实时估计,从而获得当前时刻的状态估计;用函数逼近的方法对目标的航迹进行拟合,预测命中时刻的目标轨迹作为虚拟目标;设计基于虚拟目标的中制导与修正比例末制导的导引策略进行目标拦截。
1 目标运动学建模
采用超燃冲压发动机的高超声速飞行器,飞行阶段可分为助推段、巡航段和下压段。由载机发射后进入助推段,由助推器推进到适合超燃冲压发动机工作的海拔高度和马赫数;获得足够的速度后,高超声速飞行器通过超燃冲压发动机加速到6马赫以上开始巡航段飞行;在接近目标后发动机停止工作,飞行器降高降速进入下压段,导引攻击地面目标。目标运动轨迹如图1所示,其中雷达在坐标原点实时测量目标的位置和角度信息。
目标运动学方程为
式中:x(t)为目标在惯性系中沿X、Y、Z轴的位置、速度和加速度;A为模型描述矩阵;w(t)为过程噪声。此处:
x(t)=[r(t)v(t)a(t)]T
其中:
r(t)=[x(t)y(t)z(t)]
v(t)=[vx(t)vy(t)vz(t)]
a(t)=[ax(t)ay(t)az(t)]
量测方程为
zk=h(xk)+vk
式中:h(xk)为地面雷达能测量到目标的位置、俯仰角和方位角;vk为量测噪声。
1.1 Singer模型
SINGER针对机动目标提出了零均值一阶时间相关的加速度模型,称为Singer模型,是对机动目标加速度建模的一个典型模型,因此本文选用Singer模型描述目标的运动。假定机动加速度a(t)为一阶时间相关过程,其时间相关函数为指数形式,有
Ra(τ)=E[a(t)a(t+τ)]=(σa)2exp(-λ|τ|)
式中:(σa)2,λ为在区间(t,t+τ)内决定目标机动
特性的待定参数,λ≥0[12-13]。其中:(σa)2为机动加速度方差;λ为机动时间常数的倒数,即机动频率,通常经验取值为转弯机动λ≈1/60,逃避机动λ≈1/20,大气扰动λ≈1,其准确值通过实时测量才能确定[14]。
对Ra(t)应用Wiener-Kolmogorov白化程序后,即动加速度a(t)可用输入为白噪声的一阶时间相关模型表示,则有
式中:w(t)为均值为零、方差为2λ(σa)2的高斯白噪声。
一个方向的目标Singer运动学模型在雷达测量坐标系中可表示为
式中:x,wx分别为目标的位置和加速度噪声。
1.2 量测模型
设对位置R、俯仰角θ和方位角φ的目标,地面雷达量测值分别为Ro,θo,φo,则量测方程可表示为
Ro=R+wR
θo=θ+wθ
φo=φ+wφ
式中:wR,wθ,wφ分别为量测噪声。为便于线性化处理,将雷达信息分解为雷达三轴测量方程
xo=Rocosθocosφo
yo=Rosinθo
zo=Rocosθosinφo
式中:xo,yo,zo为测量值变换处理后的虚拟测量值[15-16]。以yo为例(xo,zo的概率特征求取方式相似),有
yo=Rosinθo=(R+wR)sin(θ+wθ)=
Rsinθ+Rwθcosθ+wRsinθ+wRwθcosθ
其期望值和方差分别为
E(yo)=Rsinθ
则,分解的Singer模型对应的量测矩阵为
2 轨迹预测与拦截
2.1 轨迹预测
2.1.1 运动参数估计
用扩展卡尔曼滤波算法估计飞行器的状态参量。飞行器运动方程是连续系统,而雷达量测值是离散的,因此本文用离散卡尔曼滤波算法估计飞行器的状态参量。状态参量


P0=E[(x-x0)(x-x0)T]
a)时间预测
Φ(Ts)=e(Ts)=

b)量测更新
Kk=Pk(Hk)T(HkPk(Hk)T+Rk)-1
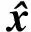
矩阵9个元素分别为

2.1.2 轨迹预测
典型的轨迹预测方法,通过滤波估计目标的运动参数为预报提供准确的初值。获取目标运动参数后,用解析法计算或数值方法迭代获取目标运动轨迹。理论上,任何一个运动轨迹都可用多项式描述。虽然用多项式逼近目标运动轨迹时的近似性较好,但对跟踪系统来说,并非适于任何情况。在建立逼近模型进行轨迹预测时,为使建立的模型既符合机动实际又便于数学处理,本文取n=2数学模型描述目标弹道倾角和弹道偏角,有
θt(t)=a0+a1t+a2t2
φt(t)=b0+b1t+b2t2
用三阶数学模型描述目标的速度特性,即
vt(t)=c0+c1t+c2t2+c3t3


2.2 拦截策略
本文综合目标运动状态估计和弹道预测结果,设计目标机动和弹道预测在中/末制导律中的补偿算法,满足多约束条件的中/末制导律。通过对弹目交会剩余飞行时间的估计,用轨迹预测法预测命中时刻目标轨迹,将预测命中时刻目标作为虚拟目标。中制导采用基于虚拟目标的拦截方法,同时考虑约束拦截交会角

在末制导段采用修正比例制导

为避免中末制导段弹道交班的过载抖动,设中末制导过渡段制导指令为
nyc=kpnym+(1-kp)nyt
nzc=kpnzm+(1-kp)nzt
式中:kp为距离的函数,取值范围0~1,当距离大于中末制导交班过渡段时值为1,随距离接近末制导段最终变化为0。
3 仿真
对典型高超声速飞行器飞行末端,验证利用系统的状态估计信息预测目标轨迹精度和基于虚拟目标的中/末制导律拦截可行性。雷达测量值包含目标距离、高低角和方位角,设雷达参数性能参数为:ρ,θ,φ的测量误差分别为20 m,0.1°,0.1°(1σ)。
用本文方法对目标轨迹进行预测,同时考虑高超声速飞行器的约束条件,仿真所得高超声速飞行器典型攻击时的弹道倾角、导弹速度规律和预测轨迹分别如图2~4所示。
由图2~4可知:对目标的预测轨迹误差随时间而增大,利用初始的预测结果会造成中制导较大的误差。为减少中制导误差,拦截过程中实时更新一次虚拟目标的预测结果,随着弹目交会剩余时间的减少,中制导预测精度逐渐提高,从而为末制导创造有利条件。
中制导预测的虚拟目标位置与拦截时刻目标的真实位置如图5所示。由图5可知:随着剩余飞行时间减少,对虚拟目标预测所需时间减少,预测位置与最终拦截点目标位置逐渐接近,本文采用的实时给出一次虚拟目标位置的策略有效。
高超声速目标拦截过程采用虚拟目标中制导,中制导阶段实时预测目标位置,随着弹目的接近过载曲线不断收敛,末端切换至修正比例制导过载。仿真所得采用虚拟目标中制导律的导弹拦截轨迹如图6所示。由图6可知:采用虚拟目标的制导方式拦截高超声速飞行器,能实现较小的弹目交会角,交会角小于15°,弹道过渡较平滑,中段需过载接近15g,末端需用过载小于10g。
4 结束语
本文对一种基于虚拟目标的新型制导策略用于高超声速飞行器拦截制导律进行了研究。用扩展卡尔曼滤波器估计目标运动信息,结合最小二乘法和估计的运动信息拟合运动模型系数,对预测命中点进行弹道倾角、偏角和轨迹预测;将预测命中点作为虚拟目标点开展中制导,修正弹道偏差的同时约束弹目交会角,进入导引头作用距离后逐渐切换至末制导律。与传统方法相比,本文设计的拦截策略能有效约束末端弹目交会角,有助于拦截弹准确飞往预测命中点,减少拦截弹过载需求,降低拦截弹的设计难度。本文方法不仅适于高超声速飞行器拦截,而且适于其他大机动目标的轨迹预测与拦截。所提方法中轨迹预测精度是影响最终拦截精度的重要因素,为进一步提高预测精度,后续可对滤波精度和轨迹预测模型进行研究[17]。
[1] 秦雷, 李君龙, 周荻. 临近空间非弹道式目标HTV-2跟踪滤波与预报问题[J]. 航天控制, 2015, 33(2): 56-61.
[2] 魏喜庆, 王社阳, 李瑞康. 基于自适应IMM算法的高超声速飞行器轨迹预测[J]. 上海航天, 2016, 33(2): 27-31.
[3] 张晶, 贺正洪, 王博. 临近空间高超声速发展及防御策略研究[J]. 飞航导弹, 2015(4): 25-29.
[4] DWIVEDI P N, KUMAR P, BHATTACHARYA A, et al. Lead angle constrained optimal midcourse guidance: AIAA Guidance, Navigation, and Control (GNC) Conference[C]// Boston: 2013.
[5] CHEN C H, LIANG Y W, LIAW D C, et al. Design of midcourse guidance laws via a combination of fuzzy and SMC approaches[J]. International Journal of Control, Automation, and Systems, 2010, 8(2): 272-278.
[6] EVCIMEN C, LEBLEBICIOGLU K. An adaptive, optimal proportional-integral guidance for missiles: AIAA Guidance, Navigation, and Control (GNC) Conference[C]// Boston: 2013.
[7] YAMASAKI T, BALAKRISHNAN S N, TAKANO H, et al. Second order sliding mode-based intercept guidance with uncertainty and disturbance compensation: AIAA Guidance, Navigation, and Control (GNC) Conference[C]// Boston: 2013.
[8] LIANG Y W, CHEN J Y, LIN L G. A guidance law design using the combination of ISMC and SDRE schemes: IEEE International Conference on System Science and Engineering[C]// Budapest: 2013.
[9] SHAFIEI M H, BINAZADEH T. Application of partial sliding mode in guidance problem[J]. ISA Transactions, 2013, 52: 192-197.
[10] HEXNER G, PILA A W. Practical stochastic optimal guidance law for bounded acceleration missiles[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(2): 437-445.
[11] HU S G, FENG Y W, GAO X. A new optimal guidance law for near space hypersonic vehicle based on markov jump linear system[C]// Chinese Control and Decision Conference. [S. l.]: [s. n.], 2011: 478-482.
[12] 邓自立. 自校正滤波理论及其应用: 现代时间序列分析方法[M]. 哈尔滨: 哈尔滨工业大学出版社, 2003: 161-192.
[13] 周宏仁, 敬忠良, 王培德. 机动目标跟踪[M]. 北京: 国防工业出版社, 1991: 10-24.
[14] ZARCHAN P. Tactical and strategic missile guidance[M]. Reston: Progress in Aeronautics and Astronautics, 2012: 439-471.
[15] 刘毅. 自适应交互式多模型滤波在被动制导中的应用[J]. 现代防御技术, 2009, 37(2): 41-45.
[16] BAR-SHALOM Y, K CHANG C H, BLOM A P. Tracking a maneuvering target using input estimation versus the interacting multiple model algorithm[J]. IEEE Transactions on Aerospace and Electronic Systems, 1989, 25(2): 296-300.
[17] 韩春耀, 熊家军. 高超声速飞行器弹道预测方法研究[J]. 飞航导弹, 2016(2): 24-27.
StudyonTrajectoryPredictingandMidcourse/TerminalGuidanceagainstHypersonicVehicle
LI Geng-ze1, WEI Xi-qing2, WANG She-yang2
(1. The Unit 92941 of CPLA, Huludao 125000, Liaoning, China;2. Shanghai Electromechanical Engineering Institute, Shanghai 201109, China)
Aim at the problem that the traditional guidance law was difficult to meet the demand of interception because hypersonic vehicle’s capability of fast speed and high maneuver need more required maneuvering than available maneuvering, a guidance law against hypersonic vehicle based on virtual impact point predicting was proposed in this paper. According to the Singer model of the target and measuring model, the extended Kalman filter (EKF) was applied to estimate the target motion and the virtual impact point was predicted for midcourse/terminal guidance law. With the consideration of interception angle constraint, the midcourse guidance law was applied to virtual target and modified ratio steering was used in the terminal guidance. The maneuvering dither during the trajectory handoff of midcourse and terminal course was avoided through the command of terminal guidance in transition course which could be changed with the distance. The simulation showed that the guidance law against hypersonic vehicle based on virtual impact point predicting could reduce both encounter angle and required maneuvering effectively at the same time. To reduce the midcourse guidance error, the prediction of the virtual target could be renewed once in real time during the interception. The method proposed can be used in the interception of hypersonic vehicle and the trajectory prediction and interception of other high maneuvering target.
hypersonic; interception; trajectory predicting; guidance law; Singer model; extended Kalman filter; virtual target; maneuvering
2017-11-03;
2017-11-08
国家自然科学基金资助(61573115)
李庚泽(1985—),男,助理工程师,主要从事导弹试验总体技术研究。
魏喜庆(1982—),男,博士,主要研究方向为飞行器制导控制、非线性滤波和轨迹预测。
1006-1630(2017)06-0007-06
TJ765
A
10.19328/j.cnki.1006-1630.2017.06.002

