哲学视野下《瞬时变化率》的教学设计—基于数学核心素养的提升

江苏省宝应县曹甸高级中学(225803) 李兆江

哲学视野下《瞬时变化率》的教学设计—基于数学核心素养的提升

江苏省宝应县曹甸高级中学(225803) 李兆江

1 背景

作为我校的优良传统,每学年度下半学期,学校会开展“行知杯”教学比赛贯穿教学工作,以促进教师对课堂教学研讨.在十二月份,按学科对比赛评选奖项并形成对全市公开课方案.结合教学进程,《导数及其应用》一章中的难点《瞬时变化率》教学,已有过三次对全市公开教学的经历.本学期作为第四次,我们数学教研组结合平时对数学核心素养的学习,集全组同仁智慧,遵循“数学认知”与“数学育人”两条线相互交融,从哲学视野对《瞬时变化率》的教学设计总结如下,供大家参考.

2 教学设计

2.1 问题情景

情景1:请同学们解释下面两幅图中数字的涵义:

图1

图2

速度表盘中60km/h

限速标志10km/h

情景2:请同学们欣赏下面某位同学在物理课堂中与老师的一段对话.当初你在学习时,你对老师的解释有过这样的质疑吗?

生:物体在某一时刻只能在一个位置,所以在这一瞬间,物体是不动的.同样,在其他时刻,物体又位于另外一个地方,在那一时刻也是不动的.这样一来,物体就是不动的了.既然物体在每一时刻都不动,怎么会有某一时刻的瞬时速度呢?

设计缘由:依据教学的直观性原则,在前三次对全市公开教学中,经全组同仁商讨,对教材的设计顺序都作了如下处理,每次仅作微调.先是让同学们观察图3,用平均变化率显然不能刻画两个函数在区间[x1,x2]上变化的区别,进而引出研究瞬时变化的必要性.然后提出问题:平均变化率近似地刻画了曲线在某一区间上的变化趋势,那么,如何精确地刻画曲线上某一点处的变化趋势呢?当教师投影给出教材上“局部以直代曲”图片时,总有些学生窃窃私语,“这是什么?”、“想研究什么?”.不管教师作怎样的引导、启发,总感觉不能激发学生思考的主动性、积极性.反思课堂实践,从学生的认知过程来思考,确实有些突兀,显得不够自然,也缺少数学教育形态的成份.基于上述实践再作研讨,从育人与认知两个维度出发,形成本次公开教学的两个渐进性的问题情景.

图3

设计意图:对问题情景1,从简单而又感性的直觉问题出发,符合教学的亲和原则,是确保课堂高效的关键.学生经历了平均变化率的学习,再结合生活中的数学现象,能初步换醒学生对物理学中平均速度与瞬时速度的再现,并能作初步的理性思考.对问题情景2,基于情景1的功能,并考虑到学生已学完高中思想政治必修④《生活与哲学》.这样的教学设计,以感性为基点,以哲学与速度为知识基础,再通过以趣味性的悖论呈现,更能激发学生对问题的深入而又理性的探究欲望.

2.2 学生活动与师生互动

问题1:“学而不思则罔,思而不学则殆”.情景2中悖论产生的原因是什么呢?

设计意图:穿插励志语言,通过思维性很浓的趣味性悖论,力争将数学的学术形态转变为学生易接受的教育形态,激励学生要善于思考问题、提出问题,达到提智与育人的双重效果,也为本节课的深入学习提前投注思维层面的生机活力.

问题2:“时刻”是怎么来的呢?

设计意图:各种版本的新教材编写可谓用心良苦,学生对情景2中出现的改变量“Δt、ΔS”、极限思想早有体验.问题是学生仅处于静止状态的感性理解,还不能从运动、变化的角度理性分析,仅能孤立地看一个时刻(一个位置),不能顾及每一时刻与前后时刻的关联,这是悖论产生的缘由,需引领学生深入分析产生过程.

这方面涉及一个哲学的概念:整体与局部.事实上,瞬时速度考察的不是一个个孤立的时刻,而是将该时刻前后的运动状态联系起来进行分析,即考察一个时刻所在的局部.从整体与局部层面,引领学生思考、交流,感悟变量数学的思想方法,丰富学生的思维角度,进而增强学生思维品质的深刻性、全面性、系统性.

师生互动:学生独立思考,小组交流、讨论,教师适时点拨.“时刻”的前提是时间段极短,虽然“极短”,但不是没有,仍然有很微小的一时间段在变化,启发学生构造时间段[t,t+Δt],进而从运动变化、联系的观点理解“时刻”、“极限”的概念.激发学生完成必要的形式化定义,即Δt→0时,

此常数即为瞬时速度.瞬时速度,要看作极短时间段的平均速度的极限.

问题3 如何从“视觉化”的层面反映曲线在某一点处的瞬时变化呢?

设计意图从数学外部问题抽象到数学内部问题,是提升学生跨学科核心素养的常见方式.整体与局部是辩证法中对立统一规律的基本范畴,“局部以直代曲”归根到底也是哲学问题,启发学生辩证地看待“直与曲”.此时,自然过渡到教材中的“以直代曲”导入情景,充分让学生认识宏观与微观世界的科学方法,对学生科学观的形成有着重大意义.

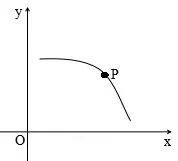
图4

师生互动:以学生自主合作为主,教师参与小组交流,察看学情.结合图4,教师作启示语:曲线在点P处曲到何种程度呢?你是如何研究微观世界的呢?当学生悟到“只可意会,不可言传”的程度,教师利用多媒体画出放大再放大的步骤与过程.

问题4:你能用联系、运动变化的观点,从数量化视角来设置微观“直线”的产生过程吗?

设计意图:割线逼近切线是从“视觉化”到“数量化”的研究历程,也是从“宏观”到“微观”的反思历程.引导学生用心体会无限逼近与“量变到质变”、“近似与精确”的哲学原理.这样的教与学过程,贯穿数与形的结合,体现了从感性知性理性,努力追求割线到切线的自然逼近,进而加深学生对导数本质的理解.

图5

2.3 建构数学(略)

2.4 数学应用(略)

2.5 回顾小结(略)

3 教学感悟

3.1 数学认知与哲学

哲学是科学皇冠上的明珠,是人生永远追忆的大智慧.整体与局部的哲学分析,为分析与综合相统一的科学方法,提供了深入阐述问题的依据.本教学设计,正是引导学生运用哲学的思维看待瞬时速度,突破了初等数学“就事论事”、孤立地考察一点,不及周围的静态思考,转而用动态的思考方法,考察“局部”,终于将直觉的瞬时速度,转化为可以言传的瞬时速度.

对立统一规律的基本范畴除了整体与局部,另外,现象和本质、原因和结果、可能性和现实性等都是对立统一规律的表现和展开,分别从不同方面进一步揭示事物的普遍联系和矛盾关系.函数、方程、不等式是通过互相转化而普遍联系,数与形是通过严谨的本质与直观的现象和谐

6.感受数学的美妙,树立战胜困难的信心,以“乐”激趣.

与物理化学等学科相比,数学是一门较为枯燥的学科,高三的复习强度大,学生遇到的困难也空前,老师要多些鼓励,少些批评,让学生感受学习数学的快乐,把思想教育渗透到教学中去.

例如在讲解三角函数的时候,我对同学们说:三角函数的图象是多么的漂亮啊,其实我们的生活就像正余弦函数,波浪起伏,有高潮也有低谷,但是我们的人生态度是应该像正切曲线一样,永远的斗志昂扬,不断向上.说完后,班里响起了热烈的掌声.

又例如,在讲导数的时候,我在班上说:我们看,是多么的忠贞不二啊,经历千万次求导依然初心不改,我们应该向它学习,为了实现自己的大学梦,坚持不懈的努力.台下又是掌声一片,大家的学习劲头更足.

再如,讲定积分的时候,我们知道可以用积分来求一些不规则图形的面积,感觉数学的应用真是奇妙;在讲双曲线的渐近线时,“无限接近但永不相交”让我们体会到极限的思想.

可见,只要我们用心去总结,学生就会发现数学的美,感受数学的魅力,就会拜倒在数学的“石榴裙”下.

数学在高考中有着举足轻重的地位,关系着高考的成败.我们要想方设法帮助学生提高学习数学的兴趣,帮助他们树立克服困难的决心,精心上好每一节课,以情趣导学,运用深入浅出的讲解、生动的语言和比喻、接近生活的例子来营造轻松快乐的学习环境,以“情、基、精、动、思、乐”激趣,充分调动学生学习数学的热情,就能提高学习的效率和效果,在高考复习备考中占得先机.