2016年全国课标I卷数学应用题列表解法剖析*

广州市第十六中学(510100) 温伙其

2016年全国课标I卷数学应用题列表解法剖析*

广州市第十六中学(510100) 温伙其

数学应用题,近几年常见于全国高考卷,是数学考查的热点.而现实教师普遍反映难教,学生感觉难学,如2016年全国课标I卷连续在选择题、填空题和解答题都出现应用题.其中第19题广东文科考生平均得分1.27,难度系数为0.106;理科考生平均得分3.08,难度系数为0.257.产生以上原因为应用题包含文字信息量巨大,变量多,回归的数学模型抽象.本文将借助2016全国课标I卷考题,分别从流程图、线性规划和概率统计三个角度进行研究,探索列表法在数学解题中的应用.

1 列表法在解题中的应用

1.1 在线性规划中的应用

【2016全国课标I卷文理第16题】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为___元.

解析:这是一道线性规划问题,这类题的特点是题目中变量比较多,约束条件隐蔽容易混淆,通过列表法可以理清各个量之间关系,清晰找到约束条件来求最优解.

设生产A、B产品数量分别为x和y,总收益为z元,列表如下:

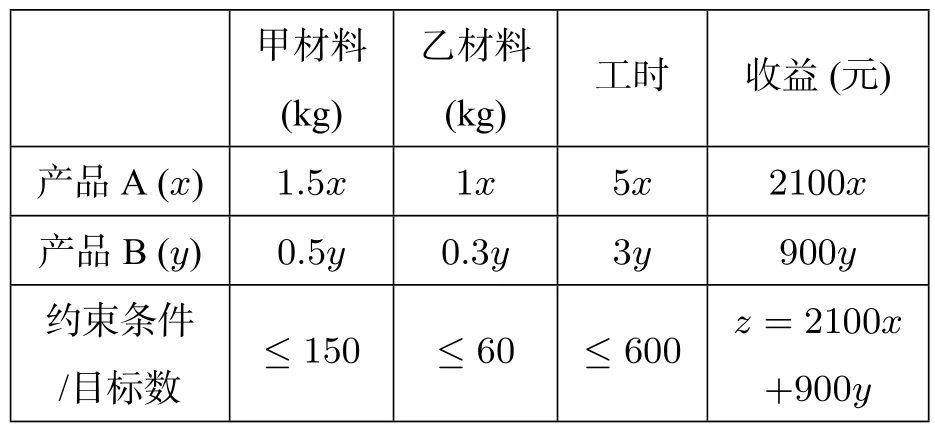
甲材料(kg)乙材料(kg)工时收益(元)产品A(x)1.5x 1x 5x 2100x产品B(y)0.5y 0.3y 3y 900y约束条件/目标数≤150≤60≤600 z=2100x+900y

根据表格数据可得约束条件为:

目标函数

作出二元一次不等式组①表示的平面区域,即可行域.如图中阴影部分所示.

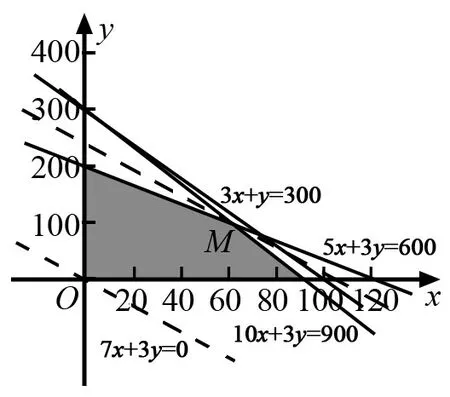
图1

变形,得

作直线

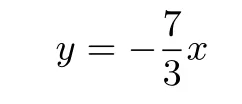
并平移,当直线

经过点M时,z取得最大值.解方程组

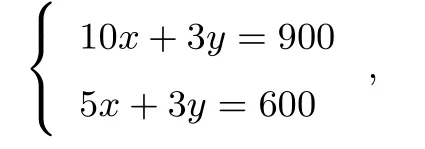
得M的坐标为(60,100).所以当x=60,y=100时,

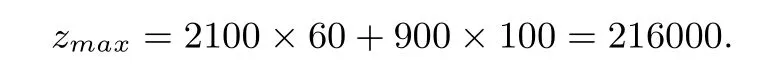
故生产产品A、产品B的利润之和的最大值为216000元.

评析线性规划应用问题,主要是正确引入二维变量,然后列齐约束条件和准确写出目标函数,难点在于约束条件的寻找.借助二维表格,能清晰发现甲材料,乙材料,工时的限制条件(即不等式),同时可以准确写出利润之和的目标函数.

1.2 在流程图中的应用

【2016全国课标I卷文科第10题】

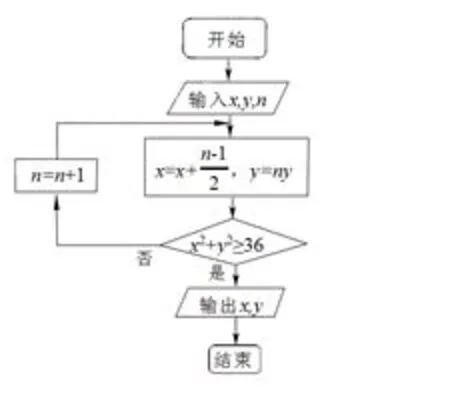
图2

执行上面的程序框图,如果输入的x=0,y=1,n=1则输出x,y的值满足( )

解析:程序框图的题目,因为变量不断的被赋值,因此通过列表的方法可以清晰的把赋值情况呈现出来,列表如下:

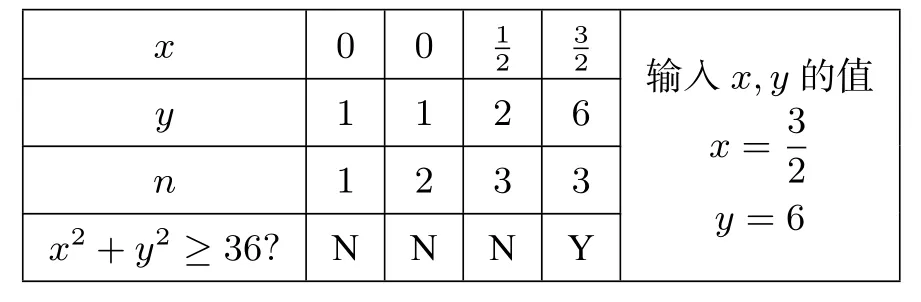
x 0 0 13 2 2 y 1 1 2 6 n 1 2 3 3输入x,y的值x=3 2 x2+y2≥36?N N N Y y=6

故选C

评析循环结构的流程图问题是算法学习中的难点,也是每年高考题中的必考点.如何能够有效破题?本题通过表格,清晰地反映了退出循环的“临界状态”,利用表格记录循环结构中判断或循环次数,以及准确“追踪”循环结构中的每一次的变量值的变化情况,不仅条理清晰,易于检查对错情况,同时可以帮助学生更容易的理解循环结构.

1.3 在概率统计中的应用

【2016全国课标I卷文科第19题】某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:

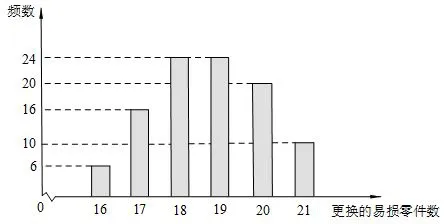
图3

记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元),n表示购机的同时购买的易损零件数.

(I)若n=19,求y与x的函数解析式;

(II)若要求“需更换的易损零件数不大于”的频率不小于0.5,求n的最小值;

(III)假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?

解析(I)由题意及频数分布表有

套餐内更换零件数套餐外总费用购买零件数费用额外购买零件数额外费用16 19 3800 0 3800 17 19 3800 0 3800 18 19 3800 0 3800 19 19 3800 0 3800 20 19 3800 1 1×500 3800+1×500 21 19 3800 2 2×500 3800+2×500 x(x≥20)19 3800 x−19(x−19)×500 3800+(x−19)×500

填完上表后,就可以得到一个分段函数解析式,进而解决问题了.所以,y与x的函数解析式为

(II)

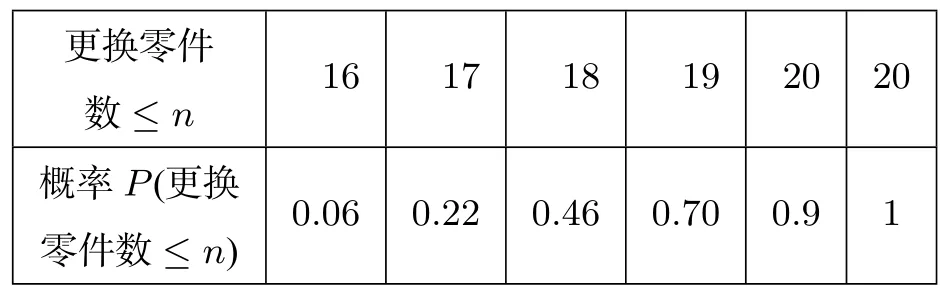
更换零件数≤n 16 17 18 19 20 20概率P(更换零件数≤n)0.06 0.22 0.46 0.70 0.9 1

所以,由上表得n的最小值为19.

(III)

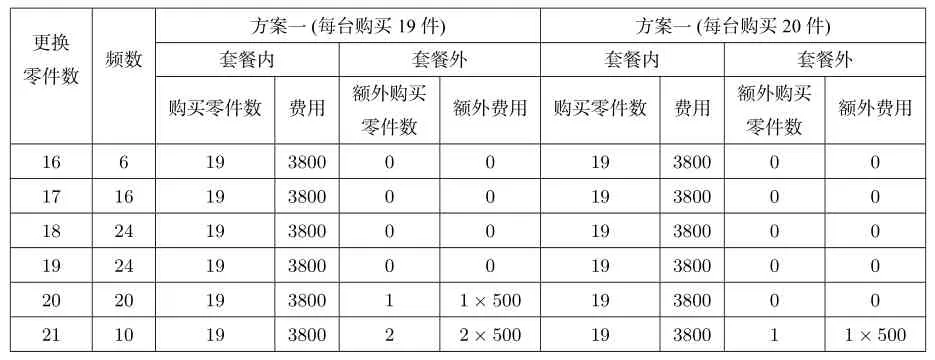
方案一(每台购买19件)方案一(每台购买20件)更换零件数频数套餐内套餐外套餐内套餐外购买零件数费用额外购买零件数额外费用购买零件数费用额外购买零件数额外费用16 6 19 3800 0 0 19 3800 0 0 17 16 19 3800 0 0 19 3800 0 0 18 24 19 3800 0 0 19 3800 0 0 19 24 19 3800 0 0 19 3800 0 0 20 20 19 3800 1 1×500 19 3800 0 0 21 10 19 3800 2 2×500 19 3800 1 1×500

由上表易得

方案一所需费用的平均数为

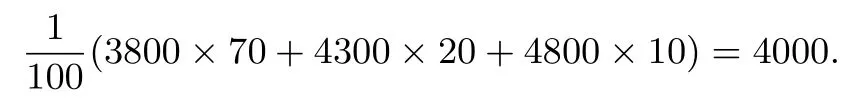
方案二所需费用的平均数为

比较两个平均数可知,购买1台机器的同时应购买19个易损零件.

评析上例三问中,包含的文字信息容量巨大,变量较多(如费用y,频数n,需更换的易损零件数x),而且分段复杂(分两次购买,两种价格),学生不一定全面辨别清楚.倘若教师能引导学生逐步把每种情况文字语言转化为图表信息,发现所需的费用分x≤19和x≥20两种情况;借助表3学生也会从图表视觉中容易清楚购买零件的费用所包括的两个方面:一是购买机器时同时购买的零件所需费用,按每个200元计算;二是备用零件不足时另外购买的零件,按每个500元计算.在此基础上,分别计算n=19与n=20两种情况下各自所需费用的平均值比较它们的大小,就可以做出正确的决策.

2 列表法解题的基本步骤

2.1 找.题目结构表格化,找出题中所有的数量关系.

(1)仔细读题,找出题目所涉及的分析对象、影响每个对象的基本对应量.

(2)把题目中已知的、未知的;同类的,不同类的;变化的、不变的数量,归类、汇集,并列表记录.

(3)将已知量的数值填入表中,未知量用“?”表示.

(4)简写“纵”、“横”关系.把数量间内在规律的固有关系即(同一分析对象不同对应量间的关系)基本数量关系作为“横”的关系;把借助草图、线段图发掘题目中的条件,破译“要语”、“关键词”以及它们赋予的数量关系(不同对象间同一对应量间的关系)作为“纵”的关系.

题目结构表

2.2 设.选设适当的未知数.

2.3 表.据部分数量关系,用已知数和未知数的代数式表示表格中的“?”.

2.4 建.根据2.3中尚未利用的数量关系建立数学模型.

2.5 解.选用适当的数学方法,求解数学模型.

2.6 答.检验并依题意选择合理的答案.

总的来说,列表法是建立数学关系于实际应用的一种好方法.它便于分析比较、提示规律,形象理解.通过表格有助于分析比较复杂的数学关系,有助于揭示概念之间的联系,有助于系统掌握知识,是值得采用的一种教学方模式和解题方法.

*本文系广州市越秀区教育科学“十三五”规划立项课题—基于视觉化表征高中数学应用问题的教学研究(课题批准号:越学科类[2016]08)和广州市越秀区科技工业和信息化局立项课题—基于视觉化表征高中数学应用问题的教学研究(课题批准号:软科学研究计划2016-JY-012)阶段性研究成果.