混合教学模式下线性代数课程改革探索

王翠芳

【摘要】 本文主要探讨了应用型人才培养目标下线性代数课程的混合式教学改革思路，以案例教学为依托，突出实用性;利用UMU互动平台，开展线上教学;融入数学实验，体现应用性;借助思维导图，促进知识系统化.通过综合运用数字化教学平台，加大案例教学与实验教学的比重，可以有效提高学习效率与教学质量.

【关键词】 案例;UMU平台;数学实验;思维导图

【基金项目】 2016年天津市教育科学“十三五”规划课题——应用型人才培养模式下大学数学教学改革研究（HE3040）.

线性代数是高等院校理工科、管理类等专业开设的一门重要的公共基础课程，其理论与方法已经被广泛地应用于工程技术、人工智能和网络通信等领域，对经济和社会生活都产生了深远的影响.线性代数主要以讨论空间中线性关系的理论和方法为主要内容，概念抽象，定理复杂，计算烦琐.但目前很多高校仍以理论教学为主，沿用传统的“ppt+板书”的灌输式学习，学生参与课堂的积极性比较低.教学内容上虽然增加了一些应用，但大多数用在内容导入上，缺少真实性、情境性和操作性，主要教学内容与实际应用或专业学习衔接不够紧密.学生被动地接受大量抽象的符号、公式和程序化的逻辑运算，久而久之产生厌烦情绪，逐渐失去兴趣，也就很难在后续专业课中学以致用.

在应用型人才培养模式下更注重对学生应用能力、实践能力与创新能力的培养，因此，线性代数课程的教学不仅肩负着让学生掌握基本理论知识的职责，更重要的是有效培养学生的数学应用能力，帮助他们形成良好的学习习惯，掌握有效的学习方法，促进综合能力的提升.多年教学实践表明，充分利用数字化教学平台，借助信息化手段，加大案例教学与实验教学的比重，有助于调动学生的积极性和主动性，增强了课程的实用性和应用性，是全面提升教学质量的重要途径.

一、以案例为依托，突出实用性

在教学中融入有实际背景的案例，有利于激发学生的学习兴趣，能够更好地体现线性代数的应用性和服务性，也有助于提高学生分析问题的能力，从而提高课堂效率和教学质量.教材中也提到了很多比较具有代表性的案例，比如，人口迁移问题、投入产出问题、城市间的航班路线图、生物种群增长问题、平板温度测量问题等[1].针对不同专业背景的学生，可以选择不同的案例.例如，在介绍行列式的计算时可以借助八卦图的“玄机”，增强趣味性.

案例  随机挑选八个数字组成八卦图，比如，   1 2 3 4   5 6 7 8   ，把这些数字按列组成二阶行列式，然后逐对相乘再进行加减运算，不管怎样选取数字，最后结果都是0.你能破解八卦图的“玄机”吗？

解  第一次：前两列，后两列组成的二阶行列式相乘取加号.第二次：第一三列，二四列组成的二阶行列式相乘取减号.第三次：外圈与内圈两个二阶行列式相乘取加号，即

事实上，这与四阶行列式按照拉普拉斯定理展开的结果完全吻合，

1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8  =2   1 2 5 6    3 4 7 8  -  1 3 5 7    2 4 6 8  +  1 4 5 8    2 3 6 7   =0.

任意选择8个数，组成八卦图   a1 a2 a3 a4   a5 a6 a7 a8   都有同样结论.

面对理工科专业的学生，也可以引入如下问题.

案例  现有一堤坝发生管涌，江水不断地涌出.假定每分钟流出的水量相同.现有四台水泵，预计30分钟可以抽完;如果再增加四台水泵，预计12分钟可抽完.为保证安全，需在8分钟之内抽完水，问至少需要多少台水泵？

解  设开始抽水前已存水量为x，管涌时每分钟流出的水量为y，每台水泵每分钟可抽水z.如果有m台水泵，抽完水需t分钟，依题意，得

x+30y-120z=0， x+12y-96z=0， x+ty-mtz=0.

这是一个关于x，y，z的三元齐次线性方程组，依题意有非零解，所以系数行列式

D=  1 30 -120 1 12 -96 1 t -mt  =0，得t= 1 440 18m-24 .

因為要在8分钟内抽完水，所以t<8，即 1 440 18m-24 <8，解得m>11.33，也就是说要在8分钟内抽完水，至少需要12台水泵.该计算过程可通过 Matlab软件实现.

二、利用UMU互动平台，开展线上教学

作为全校非数学专业的公共基础课，线性代数往往采取大班授课，近百人的课堂容量，使得课上的交流讨论，解惑答疑变得比较困难，而且很多情况下教师不能掌握学生 的真实学习情况，有些学生上课听讲状态，作业做得都不错，但一到考试就完全不知所云，这也让教师头疼不已.另一方面，随着网络与智能手机的迅速普及，ppt+黑板的传统教学模式很难激起学生兴趣，因此，有必要将传统学习方式和数字化学习结合起来，优势互补.对教师来说，既能充分发挥引导作用，又有更多机会监控教学过程;对学生而言，更能体现积极参与、发挥创造的主体性地位.目前很多网络平台，如微信公众号，蓝墨云班课，UMU互动平台等都已成为学生学习的重要载体.

UMU互动学习平台是一款综合性软件，既可以通过手机端也可以通过浏览器访问，包含签到、拍照上墙、游戏、提问、讨论、抽奖、考试等功能，其中最具特色的是屏幕投射，教师可以利用手机应用端拍摄课堂活动的照片，比如，学生的解题过程或讨论场面都等可以即时展示在大屏幕上[3].由于线性代数在行列式计算，矩阵的变换时运算量都比较大，屏幕投射功能在课堂上能够充分体现优势，教师能够针对学生的解题过程更方便地进行评价，既提高了效率，也能激发师生之间产生情感共鸣，有助于更好地教学.

课前通过UMU互动平台发布教学内容，方便学生预习，教师可以实时监控学生的预习进度，并通过提问的方式检验学生的预习效果.课上，教师精讲精练，重点突出，也可以通过UMU平台组织讨论，多种教学方式交替进行，有助于凝聚学生注意力，提高课堂效率.课下，学生可以通过平台提交图文作业，教师随时随地进行批改，提供个性化指导.借助在线学习平台，可以轻松实现课程的课前、课中、课后的有效衔接，掌控学生学习的进度和深度，还有助于更深刻地了解学生，有些学生课堂上沉默寡言，但是线上却互動活跃.线上学习情况也将作为学生平时成绩的构成.对学生而言，能够充分利用碎片化时间，扩展了学习时间与空间，也可以自己把控学习节奏，自主、独立地根据自己所需进行个性化的学习.

三、融入数学实验，体现课程应用性

目前，线性代数在图像处理、工程计算、经济学等领域发挥重要的理论基础作用，面对多变量的复杂问题，通过笔算或计算器，不仅浪费了大量宝贵的时间，而且还大大挫伤学生的积极性，所以加强学生的线性代数应用能力与计算能力是时代发展的需要.将课堂教学和计算机操作有机结合起来，把复杂的线性代数问题简单化、具体化，既培养了学生对数学的应用意识，也提高了学生动手实践的能力，保证了教学质量.

MATLAB以其简单、实用、易于操作等特点深受教师们推崇，也是在数学建模竞赛必会的一种软件.线性代数中绝大部分计算如线性方程组的求解、行列式、矩阵等都有现成的程序，因此，很多高校将MATLAB引入到线性代数的教学中.比如，要求矩阵的特征值，特征向量，将矩阵对角化，教材中需要用两至三页的篇幅，但用MATLAB只需一个命令即可，优势非常明显.比如，对于常见的斐波那契数列的求解问题，通过MATLAB软件几分钟就可以轻松解决，但笔算的话却需要很长时间且容易出错.

案例  意大利数学家裴波那契提出著名的兔子繁殖问题[4]：一对小兔子（一雄一雌）出生一个月后，每个月可以生出一对小兔子，小兔子经过一个月后也可以繁殖.现有一对小兔子，假定兔子会一直繁殖下去，没有死亡，问第n个月月初会有多少对兔子？

解  每个月兔子的对数构成的数列就是著名的Fibonacci数列{Fn}：

满足条件F0=0，F1=1，F2=1，Fn+2=Fn+1+Fn（n=1，2，3…）

由关系式 Fn+2=Fn+1+Fn， F1=F2  （n=1，2，3…）.

令 A =  1 1 1 0  ， α n=  Fn+1 Fn  ， α 0=  F1 F0  =  1 0  ，

则上述关系可写成矩阵形式 α n+1= Aα n，递推可得 α n= A n α 0.

于是求Fn的问题归结为求 α n，即求 A n的问题.

在MATLAB中输入命令：

A=sym（′[1 1;1 0]′）

[P，D]= eig（A）

得 A 的特征值矩阵 D =   1+ 5  2  0 0  1- 5  2   ，特征向量矩阵 P =   1+ 5  2  1 1  1- 5  2   ，

再由 P -1 AP = D 得， A = PDP -1， A n= PD n P -1，

在MATLAB中直接输入公式 A n= PD n P -1，计算出 A n，再输入

Fn+1 Fn  = α n= A n  1 0  ，很容易计算出Fn= 1  5     1+ 5  2  n-  1- 5  2  n ，

代入任一整数，都可计算出Fn的值，比如，F20=6 765，F30=832 040，即20个月后约有6 765对兔子，30个月后有832 040对兔子.通过MATLAB软件几分钟就可以轻松解决，但笔算的话需要的时间就很长了.

四、借助思维导图，促进知识系统化

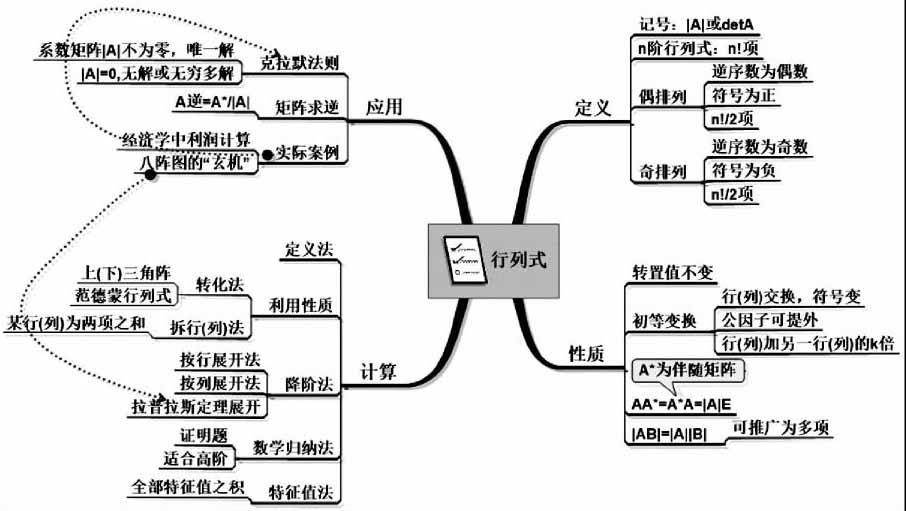
思维导图（mindmap）是由英国托尼·巴赞提出，是一种有效的思维模式.思维导图是用图解的形式和网状的结构，加上关键词和图像，表达知识点的逻辑顺序关系，从而挖掘人的记忆、创造性、机体等各方面的潜能[5].线性代数知识点纷繁复杂，通过思维导图对知识进行复习和整理，有助于学生理清知识脉络，抓住主要问题，实现教学内容的系统化和连贯性.比如，在对行列式相关知识点总结时，可以绘制如下导图：

初等行变换在线性代数中应用广泛，具有十分重要的地位，且各个部分相互关联，可以通过以下思维导图帮助学生理解记忆.

线性代数教学改革是一项长期的工程，要充分运用信息化教学手段，开展形式多样的混合式教学，最大化弥补传统教学模式在空间、时间的限制，努力提升教学的针对性和有效性.在课程建设改革过程中，教师也要不断提升信息化能力，要从授之以鱼，转变为授之以渔，成为学生获取知识的推动者，力求做到教育教学理论与信息技术的深度融合，教学相长，为培养具备综合能力的高素质人才奠定基础.

【参考文献】

[1]文军，屈龙江，易东云.线性代数课程教学案例建设研究[J].大学数学，2016（6）：46-52.

[2]杨文霞，何朗，彭斯俊.基于SPOC和翻转课堂的线性代数混合式教学改革与实践[J].大学数学，2017（4）：44-50.

[3]许麒麟，黄威荣.四种常见的课堂在线互动平台比较研究[J].教育现代化，2017（10）：174-177.

[4]黄秋和，莫京兰，宁桂英.线性代数[M].武汉：武汉大学出版社，2016.

[5]东尼博赞.博赞学习技巧[M].卜煜婷，译.北京：化学工业出版社，2015.