基于遗传算法的在线考试系统组卷设计

胡木林

摘 要 在线考试系统的核心是组卷算法，利用全局择优的遗传算法研究在线考试系统的组卷过程，解决了在线考试系统的核心技术。基于遗传算法的在线考试系统的实现缩短了考试的工作流程，减轻了教师的工作量，使考试更客观、公正、环保、高效。

关键词 互联网+；在线考试系统；遗传算法；组卷算法

中图分类号：TP319 文献标识码：B

文章编号：1671-489X（2018）12-0023-05

1 前言

2015年，国务院总理李克强在政府工作报告中首次提出“互联网+”行动计划，全面实施网络强国战略。“互联网+”模式已成为各行各业发展的新业态，互联网教育已成为教育发展的必然趋势。基于互联网的在线无纸化考试是集考试报名、制卷、阅卷、成绩统计与分析等为一体的多功能考试形式，因具有高效、客观、公正、安全、环保等一系列优点，成为国内外学校教育教学改革重要课题。

在线考试系统的核心部分就是组卷算法，它直接决定着考试检测的效果。近年来，组卷算法的研究一直是在线考试系统的研究重点，例如：刘洋进行了考试系统中组卷算法的研究与设计[1]；沈建强等研究了组卷系统的优化与实现[2]；刘彬研究了遗传算法在试题组卷中的应用，重点研究了选取的有效规则[3]。

本文重点研究具有全局优化的遗传算法，并按照试卷信度、效度、难度、区分度等评价指标，建立目标矩阵和目标函数，对遗传编码、遗传算子、算法终止条件等进行详细分析与设计。并在遗传操作的过程中研究采用分段实数编码方式和指数比例变换方式建立适应度函数，确保随机生成的试卷更科学、规范、高效。

2 选题理论

考试需要试卷，试卷质量的好坏直接决定着检测结果的真实性和代表性。因此，在线考试系统如何按照教师的要求自动制出科学、规范、全面的试卷，就体现得尤为重要。系统设计时，采用何种智能算法决定着组卷的质量和效率。目前，较为常用的有误差补偿、随机抽取和遗传算法等多种组卷算法，无论采用何种组卷算法，都必须要解决自动按照设定约束条件，选择符合要求的试题，组成考卷。试卷形成后，要按照特定评价指标给予评价。通常，其评价指标主要有信度、效度、难度、区分度和实用性等[4]。

试题的难度 难度作为试题的评价指标之一，是指试卷中试题的难易程度，用该题的通过率或平均得分率[5]来衡量，一般用P表示。主观题难度系数和客观题难度系数的计算方法如下。

1）主观性试题的难度，基本公式：

2）客观性试题的难度，基本公式：

上述公式是基于理论分析与推导，实际应用中，信度按以下方法计算。

主观题信度按克朗巴赫公式法估算：

式中，K指整个测验的题数，Sx2指测验的总得分方差，Si2指每道题的得分方差。

客观题的信度按库德—理查逊公式估算：

试题的效度 效度是指测量的有效性程度，用R表示。在教育考试领域，相较于信度而言，效度的衡量结果更加重要。在测量理论中，效度为有效分数方差与实得分数方差之比，即：

由上式可知，误差方差越小，有效分数方差越大，效度越高。

区分度 区分度用来反映试题区分不同水平参试者的程度，同时用来衡量考试试题对参试者水平差异的鉴别能力，即通过考试，能把优秀、中等、差等不同层次的学生真正区分开。区分度越高，层次划分越合理；反之，区分度越低，考试分数分布就会出现某一区间相对集中，層次划分越不合理。区分度用D表示，通常采用鉴别指数法计算：

式中，PH指高分组（即得分最高的27%）该题的正确率，PL指低分组（即得分最低的27%）该题的正确率。

试题区分度介于-1～+1之间，若值大于0.4，该题的区分度很好；若值介于0.3～0.39，该题的区分度较好；若值介于0.2～0.29，该题区分度较差，需修改；若值小于0.19，该题区分度差，需要淘汰删除该题。

3 遗传算法组卷设计

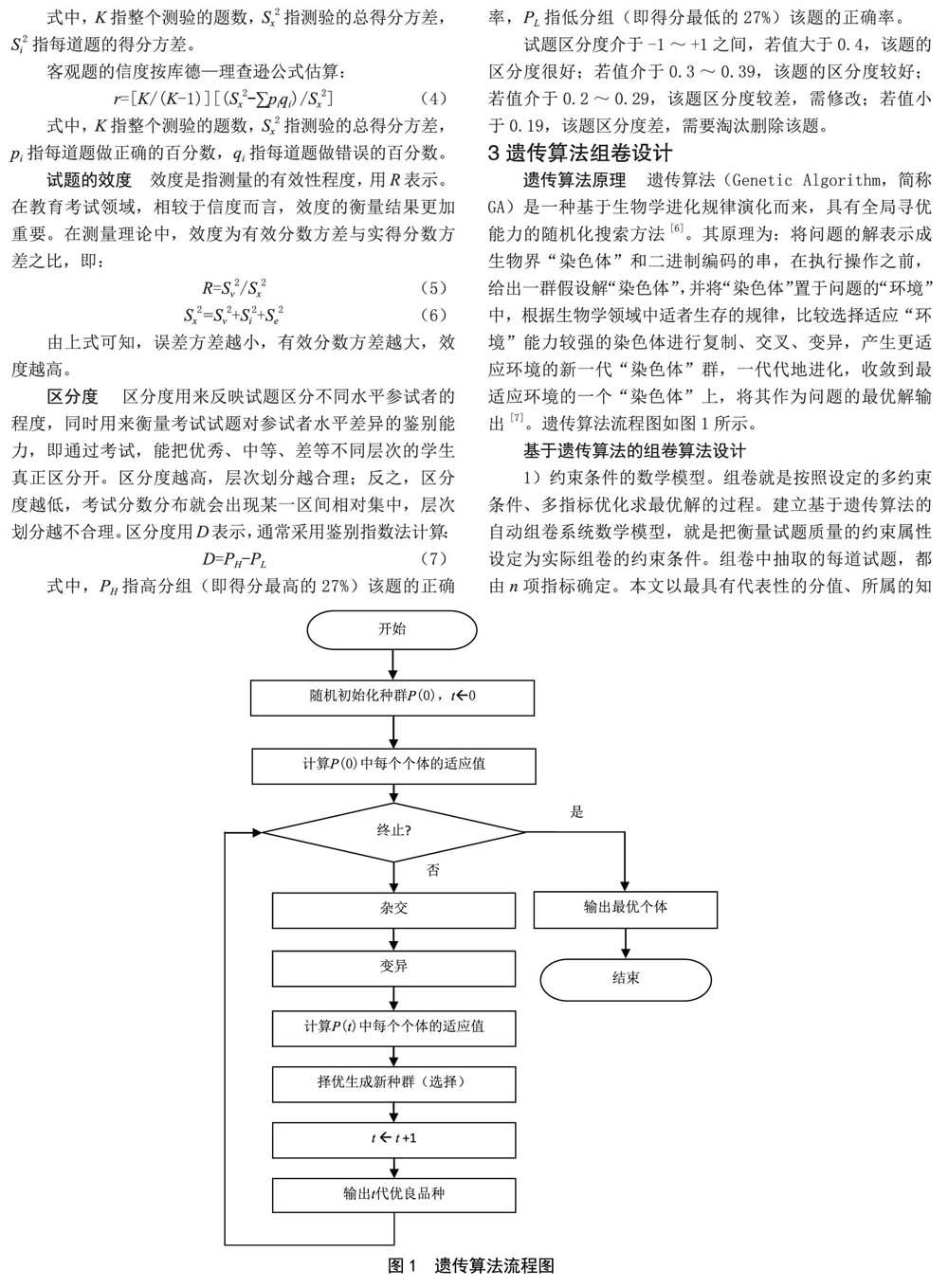
遗传算法原理 遗传算法（Genetic Algorithm，简称GA）是一种基于生物学进化规律演化而来，具有全局寻优能力的随机化搜索方法[6]。其原理为：将问题的解表示成生物界“染色体”和二进制编码的串，在执行操作之前，给出一群假设解“染色体”，并将“染色体”置于问题的“环境”中，根据生物学领域中适者生存的规律，比较选择适应“环境”能力较强的染色体进行复制、交叉、变异，产生更适应环境的新一代“染色体”群，一代代地进化，收敛到最适应环境的一个“染色体”上，将其作为问题的最优解输出[7]。遗传算法流程图如图1所示。

基于遗传算法的组卷算法设计

1）约束条件的数学模型。组卷就是按照设定的多约束条件、多指标优化求最优解的过程。建立基于遗传算法的自动组卷系统数学模型，就是把衡量试题质量的约束属性设定为实际组卷的约束条件。组卷中抽取的每道试题，都由n项指标确定。本文以最具有代表性的分值、所属的知识点、难度系数和题型等四个指标为例建立模型。每道题的数学模型用一个四维向量（d1，d2，d3，d4）来表示，其中d1，d2，d3，d4分别对应试题的分值、知识点、难度系数、题型四个属性指标[8]。若该试卷共有m道试题，则m×4的矩阵就表示该试卷的数学模型，如式（8）所示，也称为试卷目标矩阵。

目标矩阵建立后，需建立目标函数。在组卷过程中，授课教师根据专业不同，确定考试的章节和知识点，并确定相关章节在本次考试中所占的分值以及在组卷时本章所允许的分数误差。假设试题库中共有N章知识内容，Zi（i=1，2，...，N）、Yi（i=1，2，...，N）、Wi（i=1，2，...，N）

分别表示生成试卷各章节所占的分数、组卷时设定各章节应占的分数和用户允许各章节的分数误差，则生成试卷后是否满足要求，可以用式（9）、式（10）来表达：

fzw越小，则说明分数误差越小，生成的试卷质量越高，越满足使用要求。设生成试卷的难度系数为scndxs，则计算公式如式（11）所示：

式中，di1指第i题的难度系数，N指试卷的总题数。

若教师指定的难度系数为zdndxs，则难度系数误差ndwc为：

根据式（10）（11）（12）可以得出目标函数（Fmbhs）表达式为：

Fmbhs值越小，说明试卷越符合要求。

2）遗传编码。遗传算法的操作对象是群体中的个体，并对个体不断优化。因此，必须对个体用基因链码的形式表示出来，这种编制基因链码的过程称为编码。编码技术是遗传算法的关键技术，对遗传算法的成功实现起着至关重要的作用。编码的方案和策略对遗传算子产生直接影响，特别是交叉和变异算子的功能设计[9]。常见的编码方法有二进制编码、实数编码、多参数编码和DNA编码等。

实数编码技术解决了二进制编码方式搜索空间过大和编码过长的缺点，能很大程度地提高求解速度和组卷效率。因此，本文以实数编码进行研究，将每一份试卷映射成为单独的一个染色体，每一种题型作为一个基因的编码串，被选中的每一道试题作为染色体的一个基因，且该基因为抽中试题的序号。编码的过程实际上就是将同种类型的试题标号组合成段，使得每一段编码表示一种题型，每种类型的试题单独进行实数编码，编码后染色体的个数实为试卷题目的总数。假设要组成的试卷有选择题、判断题、客观题三种题型，每种题型均有五道题目，表1为采用分段实数编码组卷后两张试卷的染色体。

3）适应度函数的确定。适应度（值）是表示个体对环境的适应能力和繁殖后代的能力[10]。适应度函数是用来判断群体中的个体优劣程度的指标，适应度越大，个体越好。在遗传算法的搜索进化过程中，适应度函数是用来评估个体或解优良程度的唯一依据，是遗传操作重要条件。为便于操作，适应度函数值必须非负值。多数情况下，对于给定约束的优化，目标函数值有正有负，这就必须要建立适应度函数和目标函数之间的映射关系来确保适应度函数值的非负。建立适应度函数f（x）和目标函数g（x）的映射关系如下：

式中dmax是一个输入值，也可以是当前所有代数值，或者是最近K代中g（x）的最大值，此时dmax随着代数会有变化。

现建立目标函数Fmbhs和适应函数Fsyhs之间的映射关系式如下：

为让优秀的染色体有更多的机会被复制，同时避免复制过多优秀的染色体充满整个种群，提高偏差较小的染色体之间的竞争力，多数采用指数比例的方法来设计适应度函数，采用比例指数法建立的适应度函数Fsydhs如下：

其中β=0.03。

4）产生初始种群。在初始种群之前，首现确定初始规模及群的大小M，初始规模的大小对组卷起着很大的影响：过大，算法效率较低；过小易早熟，无法达到最优解。在实际应用中，M一般取100左右。

5）遗传算子操作。

①选择算子。选择算子是指选择优良的个体遗传给下一代。目前，选择算子方法主要有适应度比例法、联赛选择法、Boltzmann选择法等多种方法。其中，适应度比例法又称轮赌选择法，是遗传算法中使用最多最广的一种方法。本文研究采用适应度比例法，其原理为：利用计算个体的适应度函数值来划分轮盘的比例区域，适应度越大，所占轮盘的区域就越大，被选取遗传的概率就越大。假设群体大小为M，第i个个体的适应度为Si，整个种群的适应度为Sn，那么個体i被选取的概率Pi可表示为：

具体选取过程如下：

a.计算个体的适应度Si、整个种群适应度Sn、个体被选中的概率Pi；

b.确定种群中个体的最大选择概率Pmax，并且在[0，Pmax]之间生成随机概率数R；

c.比较选取，若R

d.重复步骤b与c，至个体数目满足设定的需要条件为止。

②交叉算子。交叉算子是遗传算法的核心之处，常用单点交叉和均匀随机交叉。本文研究采用单点交叉，其原理为：先确定交叉的概率Pc，一般为0.6～0.8（执行交换个体达到60%～80%）。同理，依据选择算子的方式确定交叉的个体，并随机产生一个断点，依次两两进行交换（交换双亲断点之后的部分），原理如表2和表3所示。

基因交叉后如出现基因重复（出现相同两道题）或者顺序混乱（大序号题目在前，小序号题目在后），系统首先就要做出判断，找出重复基因或要重新排序的基因的下标范围，其方法为[11]：分别将交叉点的基因同交叉点之前和之后的基因依次比较（之前的按照从后向前的顺序，之后的按照从前向后的顺序），找出第一个比变异点小的基因和第一个比变异点大的基因，分别记录i1和i2，要替换重复的基因和重新排序的基因就在区间[i1，i2]内。假设交叉点下标为i，则两层循环就在[i1，i-1]，[i，i2]这两个区间判断，如果出现重复，按约束条件随机抽取的一个没有出现的染色体（试题的编码）将[i，i2]区间内的重复基因替换掉。新染色体中就不再出现重复基因，再将新染色体的基因重新排序即可。

③变异算子。变异是产生新个体的另一种方法，对遗传算法起着积极的作用，可以提高遗传算法的全局搜索能力和保持群体的多样性[12]。变异个体的选择以及变异位置的确定，都是采用随机的方法产生。执行过程如下：

a.初始化搜索新题的次数为零，并设置最大次数为M；

b.随机产生的概率系数Pm1，若Pm1>Pm（Pm为0.001～

0.01），基因保持不变；反之，则将依据此基因的值来确定所属题型。

c.把搜索次数J加1，如果J>M，那么将停止新题搜索，且该基因保持不变；反之，将在此题型所包含的题号范围内随机生成一个与此基因值不相同的另一整数，作为新题的题号；

d.如果选择的新题所包含的知识点与本个体中的其他题目相同，则重复c的操作；

e.基因值用新题题号替换。

表4表示变异前染色体A、表5表示变异后染色体A′，变异后如出现基因重复（如A′中第二段的6与后面基因重复），则要重新随机选取一个等位基因（题号）再进行替换；若出现顺序混乱非法时（如A′中第三段的37比后面基因36大），则首先将变异点同变异点前后的基因标号依次比较，找出顺序混乱的区间，重新进行排序。

遗传运算终止条件的设计 遗传算法是一种反复迭代的搜索过程，它通过多次进化逐渐逼近最优解，而不是恰好等于最优解，因此需要确定终止条件。常用的有以下几种方法：

1）直接规定遗传迭代次数，即预先设置一定的次数，然后按情况增加代数（可达上千次）；

2）控制目标函数的方差实现终止，即当目标函数值和实际的目标值之间的差异小于允许值时，遗传终止；

3）查看适应度的变化来确定算法是否终止，即当最优个体的适应度没有明显变化或者变化很小时，则遗传终止。

考虑组卷的实效，研究采用第一种和第三种的结合作为遗传运算的终止条件，即在预先规定的代数内有一个个体的适应度值已经满足要求，则就停止；反之则一直迭代，直到达到规定的代数为止，取出终止时的最优个体作为算法最优解输出。流程图如图2所示。

4 总结

本文深入分析了在线考试系统组卷时试题选取的相关理论，研究了基于遗传算法考试系统的目标函数的设计、适应度函数的设计、种群的初始化、遗传算子的选择、遗传算子的交叉与变异和遗传算法的终止条件。系统功能实现后，通过大量组卷实验，基于遗传组卷算法在线考试系统组卷安全、方便、快捷，很大程度减轻了教师的教学负担，提高了教学效率，具有很好的实用性。同时突破时空的界限，适应互联网教育发展趋势。

参考文献

[1]刘洋.遗传算法在考试系统中组卷算法的研究与设计[J].湖南城市学院学报，2013，22（1）：75-78.

[2]沈建强，张宝明，鄒轩.组卷系统的优化与实现[J].计算机应用，2003，23（s1）：38-39.

[3]刘彬.遗传算法在试题组卷中的应用[J].燕山大学学报，2002，26（3）：193-195.

[4]金娣，王刚.教育评价与测量[M].北京：教育科学出版社，2002：12-20.

[5]郭晓君.智能组卷策略浅析[J].科技展望，2015（32）：108.

[6]徐涛.基于遗传算法的组卷研究与设计[J].软件导刊，2014，13（12）：109-111.

[7]周艳丽.基于改进遗传算法的自动组卷问题研究[J].计算机仿真，2010（9）：319-322.

[8]莫家庆，胡忠望.基于遗传算法的组卷系统的研究与实现[J].福建电脑，2014（6）：31-33.

[9]谭新良.基于整数编码和自适应遗传算法的智能组卷算法[J].电脑与信息技术，2007（4）：33-35，62.

[10]周芳.组卷技术中遗传算法的改进研究[J].信息通信，2016（7）：31-32.

[11]潘莉.遗传算法在自动组卷中的应用方法研究[D].长春：东北师范大学，2010.

[12]林关成，吴代文.基于遗传算法的在线考试系统自动组卷策略优化[J].计算机与数字工程，2012（3）：24-26.