建筑结构设计软件重要控制参数比较
周吕斌,沈泽宏
(安徽建筑大学 土木工程学院,安徽 合肥 230601)
建筑结构设计软件重要控制参数比较
周吕斌,沈泽宏
(安徽建筑大学 土木工程学院,安徽 合肥 230601)
在结构设计中,结构的控制参数起着重要性的作用。本文利用ETABS、MIDAS/GEN与SATWE软件分别对某高层框架-剪力墙进行结构计算,并对周期比、层间位移角、刚度比、剪重比等重要控制参数进行对比分析,利用数理统计方法分析差异性,确定合适的计算方法。
周期比;层间位移角;刚度比;剪重比
目前,国内结构分析软件较多,各种软件对同一结构的计算分析结果存在一定的差异。本文以某工程结构为例,比较ETABS、MIDAS/GEN与SATWE软件计算结果的差异性。
1 工程概况
模型结构为钢筋混凝土框架-剪力墙结构,21层,高度为77.1 m。抗震设计中抗震设防为7度,场地类别为Ⅱ类,设计地震分组为第一组,场地的特征周期为0.35 s。地面粗糙程度B类,基本风压0.35 kN/m2。地震作用均采用振型分解反应谱法进行计算。第j振型i层的水平地震作用标准值为:
Fji=αjγtjXjiGi
(1)
式中:αj为j振型自振周期对应的地震影响系数(与振型周期和特征周期有关);γtj为振型参与系数(与质量,抗侧移刚度和重力荷载代表值有关);Xji为j振型i层的振型位移(与质量和抗侧移刚度有关);Gi为集中于质点i的重力荷载代表值。
2 周期比
周期比是指结构在发生扭转为主的第一个自振周期与结构发生平动为主的第一个自振周期的比值。其主要的作用是控制结构扭转的影响。该工程考虑扭转耦联,计算振型个数15,结构的阻尼比5%,地震影响系数最大值0.08。振型组合采用CQC法,即完全平方根组合法,使用该方法所得到的单向水平地震作用的响应力为:
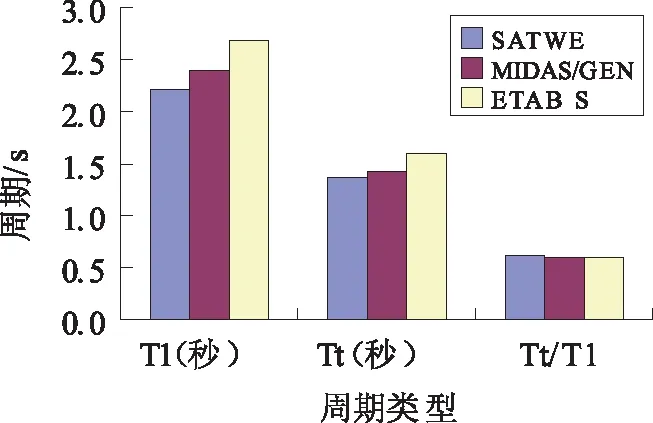
图1 周期对比
(2)
式中:Sj,Sk分别为j、k振型地震作用标准值效应;ρjk只与阻尼比和自振周期比有关。
方向组合采用SRSS法,即平方和的平方根基本方法。现将3种软件分析的结果进行对比。本实例周期折减系数为0.8。平动周期和扭转周期略有差异,如图1所示。计算出的平动周期和扭转周期大小关系:ETABS>MIDAS/GEN >SATWE。所得到3种软件计算出的周期比相差不大。
(1)哪种方法经济性更好主要取决于结构的自由度个数、刚度矩阵和质量矩阵。ETABS提供了两种方法:特征向量法和Ritz向量法,这里采用的是后者。MIDAS/GEN提供了子空间迭代法、Lanczos法、多重Ritz向量法3种,软件默认采用子空间迭代法。SATWE提供的是总刚分析方法和侧刚分析方法,这里采用的是后者。
(2)3种软件计算结构质量时,存在一定的差异比如ETABS在默认情况下可以扣除梁柱节点重合部分的质量[3],而MIDAS/GEN 和SATWE在默认情况下却不行。

图2 Y方向地震作用下最大层间位移角
3 最大层间位移角
最大层间位移角是指楼层与楼层之间最大位移与楼层高度的比值。其目的主要是保证结构具有足够的刚度和判断结构平面是否规则[4]。 3种软件在计算最大层间位移角时输出的部分结果,如图2所示。从图2可以看出,SATWE出现最大层间位移角的是第13层值为1/2616。MIDAS/GEN在第14层出现最大值为1/2483。ETABS在第16层值为 1/1796 。ETABS最大位移值是SATWE的1.46倍。在大震作用下相互之间的差异性会变得更加明显。形成差异的原因有:
(1)层位移主要受到地震作用下层剪力和柱子的抗侧移刚度的影响,从软件结果中发现各软件计算柱子的抗侧移刚度最大的相差不到0.04%。
(2)ETABS是采用壳单元的有限元法将楼板划分成一定数量的壳单元,以变形协调为原则,这种算法更接近实际[3]。而SATWE和MIDAS/GEN采用的是刚性楼板假定方法进行计算,该种方法为了简化计算存在一定的假设。这些假设减少了结构位移的自由度个数,进而影响结构振动特征方程的求解。虽然自由度个数减少会使方程的求解的精度提高,但是方程根的数目会减少,从而使结果与实际产生偏差。
4 刚度比
刚度比是指结构在不同楼层方向的侧向产生的刚度比值。其目的是控制结构竖向规则性,避免结构竖向刚度发生突变,形成薄弱层。3种软件在地震作用下都采用的是地震剪力与地震层间位移比值的方法计算刚度比,计算结果如图3所示。

图3 Y方向各楼层的刚度比
从图3可以看出,3种软件计算的刚度比从表面上看相差不大,除首层和顶层有所差异。特别是SATWE数据中顶层刚度比出现最小值。经过多次建不同模型分析SATWE顶层结果都为1,这是因为将本层刚度跟本层刚度之比的结果。所以顶层数据就没有了参考的价值。如果排除顶层的数据,SATWE出现最小值在13层为1.346 3。MIDAS/GEN和ETABS都在14层出现最小值分别为1.344 0和1.387 7。SATWE和MIDAS/GEN仅仅相差0.17%,MIDAS/GEN和ETABS相差3.15%。
通过均值方程t检验比较两两之间的差异性,设H0:两者之间无差异。当а越小即拒绝H0越困难,所以将置信区间度取越小更为合适为50%。拒绝域按公式(3)计算。
W={|T|≥tα/2(n1+n2-2)}
(3)
利用SPSS软件进行计算得出t的绝对值分别为:MIDAS/GEN与ETABS为0.370 2,MIDAS/GEN与SATWE为 0.231 4,SATWE与ETABS为0.616 2。都小于t0.25(36)=0.681 4(排除首层和顶层数据),其都在接受域以内,即可以说明差异性不明显。
5 剪重比
剪重比是对应于结构水平地震作用下标准值的楼层剪力与重力荷载代表值的比值。主要是为了控制楼层的地震剪力。在多遇地震水平地震作用计算应满足下式:
(4)
式中:λ为水平地震剪力系数。
X方向整层剪重比计算结果如表1所示。MIDAS/GEN与SATWE曲线几乎重合,而ETABS略偏低一点。

表1 X方向整层剪重比
6 结 语
(1)在求解结构振动特征方程时,ETABS软件宜采用Ritz向量法,该种方法考虑了荷载的空间性,更接近实际情况。MIDAS/GEN软件中, Lanczos法和多重Ritz向量法对收敛的判定比较模糊,而子空间迭代法精度相比较高[7]。SATWE软件中总刚分析方法和侧刚分析方法主要取决于结构有无定义弹性楼板等因素。
(2)3种不同软件对结构重要控制参数做出对比分析,就本实例工程结构而言:ETABS相比于SATWE和MIDAS/GEN在计算最大层间位移角时值略偏大而剪重比略偏小。SATWE和MIDAS/GEN之间的参数结果差异较小。另外,3种软件在计算时所用时间相差明显,在计算本实例工程时ETABS分析所花时间最长,其次是SATWE,分析所用时间最少的是MIDAS/GEN。
(3)层间位移、剪重比在各软件中计算出的主要差异性是由于计算出的地震作用下层剪力和重力荷载代表值的不同而导致,对于本工程实例而言,软件计算出的结构自由度个数,质量矩阵和重力荷载代表值不同是差异性的主要来源。
[1] 中国建筑科学研究院.GB50011-2010建筑抗震设计规范[S].2010:35-46.
[2] 王耀伟,黄宗明.对建筑结构抗震变形验算中层间位移角取值的认识[J].建筑结构,2006,(7):21-24.
[3] 北京金土木软件技术有限公司,中国建筑标准设计研究院编.ETABS中文版使用指南[M].北京:中国建筑工业出版社,2004:10-30.
[4] 云牧星,钟晓明.高层建筑需要控制的参数及调整方法[J].中国建材科技,2013(2):54-61.
[5] 中国建筑科学研究院.JBJ3-2010高层建筑混凝土结构技术规程[S].2010:12-22.
[6] 中国建筑科学研究院.GB 50010-2010混凝土结构设计规范[S].2010:7-35.
[7] 宫玉才,周洪伟.快速子空间迭代法、迭代Ritz向量法与迭代Lanczos法的比较[J].振动工程学报,2005(2):227-232.
Comparison of Important Structure Control Parameters of Different Software
ZHOU Lvbin,SHEN Zehong
(Anhui Jianzhu University,Hefei,230601,China)
Structure control parameters play an important role in the structure design,which affect directly the safety and economy of the structure. The results of different software calculation often have some differences.The ETABS,MIDAS/GEN and SATWE software are used respectively for calculation of the high-rise frame-shear wall structure to makes contrast analysis on some important control parameters,such as period ratio,Story Drifts,rigidity ratio and rigidity-gravity ratio. Mathematical statistics method is used to study difference analysis in order to determine appropriate software on the basis of the actual situation.
period ratio;story drifts;rigidity ratio;shear/gravity ratio;ETABS;MIDAS GEN;SATWE
10.3969/i.issn.1674-5403.2017.03.013
TU318
A
1674-5403(2017)03-0048-03
2017-05-20
周吕斌(1991-),男,安徽安庆人,在读硕士研究生,主要从事超高层、大跨度空间结构研究.

