框架结构滞回耗能计算方法对比分析

孙 浩，陈佩圆

(1.安徽建筑大学 土木工程学院，安徽 合肥 230601;2.中国科学技术大学 近代力学系，安徽 合肥 230026)

框架结构滞回耗能计算方法对比分析

孙 浩1，陈佩圆2

(1.安徽建筑大学 土木工程学院，安徽 合肥 230601;2.中国科学技术大学 近代力学系，安徽 合肥 230026)

滞回耗能计算常用的时程分析法对建模要求高，且计算过程复杂、工作量大，故对滞回耗能计算方法简化。本文建立了6个框架模型，考虑不同设防烈度、结构层数以及地震波峰值加速度等3因素对两种滞回耗能简化计算方法进行对比研究，给出两种常用的滞回耗能简化计算方法的精度，并提出两种计算方法的适用性。

框架结构；地震波；滞回耗能；简化计算方法

地震对结构的作用过程是地震动能量的输入、转化及耗散的过程，在遭遇较大地震作用时，结构往往以阻尼或非弹性变形的途径耗散部分地震能量而产生一定的塑性破坏。基于能量的抗震设计是在一定的地震作用下，结构耗散地震能量的能力大于所输入的地震能量，以保证结构和人员的安全。

在地震作用过程中，与结构破坏有直接联系的是结构的滞回耗能[1]。目前滞回耗能的计算常采取时程分析法去求解，该方法不仅建模要求高，而且计算过程复杂、工作量大，这制约着其在实际工程结构中的应用。尽管已提出多种滞回耗能简化计算方法，然而不同的方法简化原理不同，在实际应用过程中，会产生不同程度的误差。因此，本文以时程分析方法为基准，分析对比两种常用滞回耗能简化计算方法的精度，并给出其适用性建议。

1 滞回耗能简化计算方法

滞回耗能简化计算方法是通过一定的方法将多自由度体系与多个单自由度体系等效，通过对单自由度体系的时程分析求得在地震波作用下单自由度体系的滞回耗能，从而求得多自由度体系的滞回耗能。在简化过程中，单自由度体系的弹塑性特征是最为关键的。

1.1 振型分解方法

振型分解方法(M1)[2]通过对多自由度体系的振型分解，将其等效为具有不同振型特征的单自由度体系，求解各个振型的等效质量和等效刚度，可建立具有不同振型特征的单自由度结构。等效质量和等效刚度求解公式分别为：

(1)

(2)

式中：γj为j振型的振型参与系数；mi为i层质量；Xij为j振型i质点的水平相对位移；Pjy为j阶振型的屈服剪力；δjy为j振型的屈服位移。

在等效过程中，楼层屈服系数ξy是求解单自由度体系弹塑性特征的关键。对于一般高层建筑，可根据ξy与结构延性系数μ的关系进行求解：

(3)

各阶振型的屈服剪力和屈服位移计算如下：

(4)

(5)

式中:Fij为j振型i质点水平地震作用标准值；αj为j振型地震影响系数；g为重力加速度；ωj为j振型自振频率。

根据《建筑抗震设计规范》[3]，采用SRSS组合方式对各阶结果进行组合：

(6)

式中：n为所取的振型数，常取2阶。

1.2 Model Pushover方法

Model Pushover方法(M2)[4]利用对结构进行Model Pushover分析，求解出各阶能力曲线后，将能力曲线进行A-D格式化，并将其作为等效单自由度体系的骨架曲线。现以多自由度体系1阶振型为例介绍M2的等效过程。1阶振型的等效质量和振型参与系数计算如下：

(7)

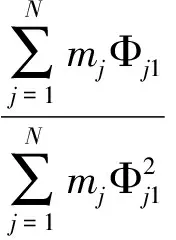
(8)

式中：Φj1为相应于1阶j层处的振型；mj为j层的质量；N结构总层数。

按Modal Pushover分析得到的能力曲线进行A-D格式化，A和D分别通过下式求解：

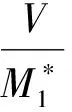
(9)

(10)

式中：V为能力曲线剪力值；U为能力曲线位移值。

将A-D格式化后的曲线作为能力曲线即可建立具有不同振型特征的单自由度体系。将多个单自由度体系计算的滞回耗能结果通过振型参与系数组合起来便得到多自由度体系的总滞回耗能。

2 分析模型

为全面比较分析两种简化计算方法的精度和适用性，分别在PKPM软件中建立6度6层、7度(0.1 g)3层、7度(0.1 g)6层、7度(0.1 g)9层、8度(0.3 g)6层、9度6层共6个框架模型，根据PKPM软件计算，选取中间一榀框架作为研究对象，在SAP2000中建立有限元模型，使用具有滞回特性的LINK单元[5]模拟塑性铰。塑性铰本构曲线由混凝土结构截面非线性特性计算软件Response2000求得，滞回模型为软件自带的考虑有刚度退化的3线型滞回模型。按M1和M2等效的单自由度体系的特征参数见文献[6]。

地震波分为3类，分别为短持时(S)、中持时(M)和长持时地震波(L)。为验证M1和M2在不同地震加速度作用下的精度，将地震波峰值加速度调幅至各模型设防罕遇地震作用的3种地震水平。各模型所选用地震波信息如表1所示，地震波持时统一选取为35 s。

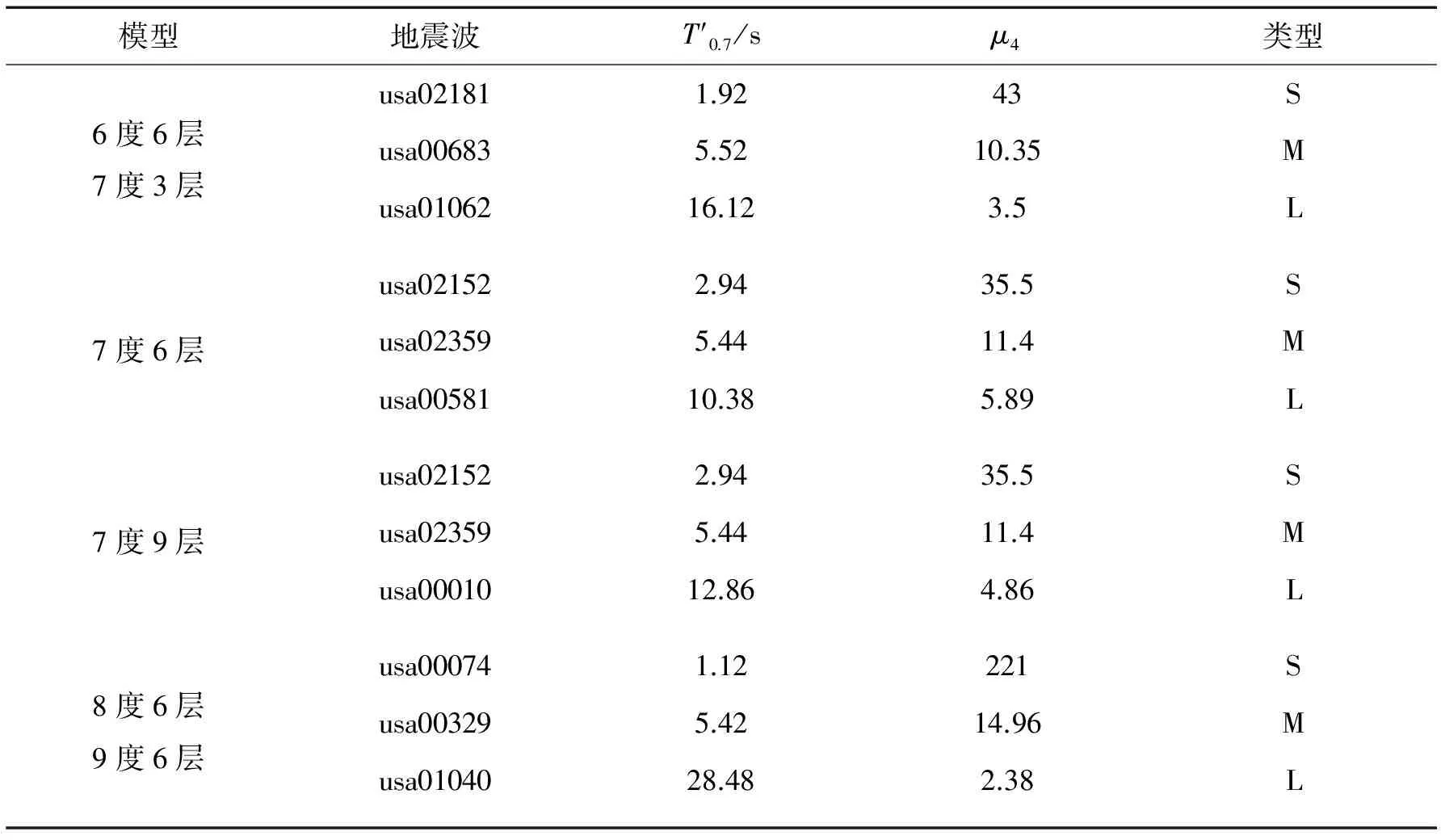
表1 地震波信息

3 计算结果分析

对6个模型分别进行时程分析、M1等效计算和M2等效计算，求出在各种方法下各模型的滞回耗能值，以时程分析计算结果为基准，对M1和M2方法计算结果进行误差分析。其中，每种滞回耗能简化计算方法的结果取3种地震波计算值的平均值，对每种简化计算方法取二阶振型结果进行组合。

3.1 设防烈度的影响

通过M1和M2两种方法计算6度6层、7度6层、8度6层和9度6层结构在不同地震作用下滞回耗能的误差分析如表2所示。

表2 滞回耗能计算结果误差

总体上，随着地震动加速度的增大，M1的误差随之增大；而M2的误差具有一定降低的趋势。随着地震加速度的增大，对于6度6层结构，M1的误差从13.6%上升至40.7%，而M2则始终低于12%，最小为5.4%。对于7度6层结构，M1的误差总体上低于6度6层结构，从5.8%上升至28.3%，而M2的误差保持在10%左右。对于8度6层结构，M1的误差分布在15%左右，而M2的误差均小于12%。对于9度6层结构，M1的误差由17.4%上升至30%，而M2的误差低于10%。

可见，对于不同的设防烈度，M2比M1具有更好的精度和适用性。并且M2的精度随着地震加速度的增大而增大，而M1在设防多遇地震下的也具有较好的精度。

3.2 层数的影响

在地震作用下，随着结构层数的增大，高阶振型的影响也越发显著。通过M1和M2两种方法计算7度3层、6层和9层框架结构滞回耗能的误差分析可得，随着地震加速度的增大，M1误差线性增大，在罕遇地震作用下，3层、6层和9层结构的M1最大误差分别为16.1%、28.3%和43.3。M2在各个工况下，计算精度都表现出了较好的稳定性，在7度3层结构中，误差均小于5%，在7度6层结构中误差均小于10%。在7度9层结构中，除在峰值加速度PGA=220×10-2m/s2时，误差为14%，其他均小于5%。

可见，随着结构层数的增大，M1的精度越来越差，而M2具有较好的精度和稳定性。

当结构遭受罕遇水平地震作用时，M1的等效结果满足精度要求，随着地震动强度的增大，精度越来越差。M2对于结构特性、地震动特性等均有较好的适用性，其精度满足要求。

M1的原理是将多自由度结构等效为理想弹塑性单自由度体系，弹塑性特征基于延性系数的求解，未考虑结构屈服后特性，故结构屈服的越充分，误差将越来越大。但是，该方法是以振型分解方法为基础的，并且简单易用，因此有着较好的工程应用前景。

M2结合静力弹塑性分析，将结构不同振型的能力曲线作为等效单自由度体系的本构，从概念上来说，是比较合理的一种等效方法。同时，该方法计算精度高，适用性好。

4 结 语

本文对两种常用滞回耗能简化计算方法的精度和适用性进行分析，并给出适用性建议。分析结果表明：M1基于振型分解法的方法在结构遭受罕遇地震作用时，具有较好的精度，且以抗震规范振型分解方法为基础，具有较好的工程应用前景；M2方法由于基于Model Pushover分析，本构关系更为合理，计算结果精度高，方法适用范围广。研究结果可为基础能量的抗震设计提供参考。

[1] 杨文星,罗少锋.单自由度体系地震能量反应的计算[J].西安科技大学学报(自然科学版),2006,26(1):40-43.

[2] Chopra Anil K.结构动力学:理论及其在地震工程中的应用[M].北京:高等教育出版社,2007: 377-405.

[3] 中华人民共和国住房和城乡建设部.GB50011-2010 建筑抗震设计规范[S].北京:中国建筑工业出版社,2010:31-43.

[4] 毛建猛,谢礼立.基于MPA方法的结构滞回耗能计算[J].地震工程与工程振动,2008;20(6):33-38.

[5] 许欢欢.基于多模态循环往复加载pushover方法对框架结构抗震性能分析[D].重庆：重庆大学,2001:22-23.

[6] 陈佩圆.基于耗能特性的RC框架结构破坏模式合理性评价[D].重庆：重庆大学,2012：17-34.

[7] 杜敏,林玮,郭晓云.基于等效单自由度体系的结构地震输入能量的研究[J].地震工程与工程振动,2011,31(3):77-82.

[8] 易伟建,尹犟.基于位移及滞回耗能的结构抗震性能评估新方法[J].湖南大学学报(自然科学版),2009,36(8):1-6.

Comparative Analysis of Hysteresis Energy Calculation Methods for Frame Structures

SUN Hao1,CHEN Peiyuan2

(1.Anhui Jianzhu University,Hefei 230601,China;2.University of Science and Technology of China,Hefei 230026,China)

At present,hysteretic energy calculation usually uses time-history analysis method,which has not only high modeling requirements,but also a complicated calculation process and a large amount of workload,so it is necessary to study the simplified calculation method of hysteretic energy consumption. Through establishing six framework models and analyzing the influence of different seismic precautionary intensity,structure layer and the peak acceleration of seismic waves on the accuracy of the two kinds of hysteretic energy simplified calculation methods. It is summarized the accuracy and applicability of the two kinds of commonly used simplified calculation method.

frame structures;earthquake waves;hysteresis energy;simplified calculation method

10.3969/i.issn.1674-5403.2017.03.007

TU311

A

1674-5403(2017)03-0024-04

2017-05-15

孙 浩(1987-)，男，安徽马鞍山人，在读硕士研究生，主要从事工程结构安全应用方面的研究.