基于行最简阶梯型的化学方程式配平法

杨 燕 妮

(喀什大学 数学与统计学院，新疆 喀什 844006)

基于行最简阶梯型的化学方程式配平法

杨 燕 妮

(喀什大学 数学与统计学院，新疆 喀什 844006)

对文献[1]利用矩阵代数配平化学方程式的方法给予了理论证明，即最终得到的解构成矩阵的零空间。因此，其解可能有无穷多。此外，将文献[1]化简矩阵为阶梯型改进为行最简阶梯型，并指出在化简矩阵为阶梯型时，只能使用行变换。重要的是，可直接利用Matlab软件来替代手工操作，避免用蛮力来执行这些行变换。

质量守恒定律；化学方程式；初等行变换行；零空间；行最简阶梯型

化学反应是指反应物和生成物的符号表示形式，它们通常位于某一特定化学方程式的左右两侧。化学反应有些是可逆的，但也有不可逆的[2]。由于化学反应式的反应物和生成物是用单箭头(反应不可逆的情况)或双箭头(反应可逆的情况)连接的，从这个意义上讲，它们不同于用等号连接左右两边的数学方程。估计化学过程中反应物数量的定量与定性知识，预测生成物的性质、数量和确定反应发生的条件，在配平化学反应式中非常重要。

如果左侧每种类型元素的原子数与右侧相应类型的原子数相同，那么称化学方程式平衡，否则称为不平衡[3]。在化学反应中，对反应物之间关系的定性研究称为化学计量[3]。总结配平化学反应式的观察法、代数法等众多方法的优缺点。简单地说，观察法要对涉及使等式相等的系数进行不断的猜测，直到方程平衡为止。代数法可以规避观察法的缺陷，所以在配平复杂化学反应式中作用较大。但是它的依据何在呢？

代数法实际上就是解齐次线性方程组。为此，可写出齐次线性方程组的矩阵(一般是稀疏矩阵)形式。因线性方程组是齐次的，故求得的解在相应矩阵的零空间中。然后，对矩阵执行初等行变换，将其化简为行最简阶梯型。本文还介绍了利用Matlab软件的rref命令将相应矩阵化简为行最简阶梯型。

本文给出的基于行最简阶梯型的配平化学反应式法，是揭示线性代数和化学计量原理之间相互联系的一个典型范例。

1 方法

关于阶梯型和最简阶梯型矩阵的相关结论，在大多数《线性代数》教科书中很容易找到。为此，本节只陈述结论，而不予证明。

引理1.1[4-5]由于矩阵的行秩等于列秩，所以对矩阵A施行初等行变换所产生的任何阶梯型矩阵的非零行和列的数目是相同的，与所使用的行变换顺序无关。

给定一个n×m阶矩阵A，化简其为行最简阶梯型的一般步骤为:

(1) 利用高斯消去法由A可产生一个阶梯形式。

(2) 在阶梯型的每个引导列中，使用最下面的非零元素1，从最右边的引导列开始向左施行初等变换，以便消去该列以上的所有非零元。

定义1.1[4-5]一个n×m阶矩阵A称为行最简阶梯型(简记为rref)，如果:

(1)它是阶梯型的(比方说，有k个非零行)；

(2)对1≤i≤k，阶数为p的单位矩阵的第i个引导列等于ei。

行最简阶梯型的唯一性是寻找矩阵零空间的基本遵循。

定理1.1[4-5](行最简阶梯型)通过初等行变换，每个矩阵只有一个行最简阶梯型，它与所使用的初等行变换顺序无关。

2 实例

例2.1 当铁和氧之间发生化学反应时形成锈。该化合物是覆盖在铁表面的红褐色鳞片。锈是分子式为Fe2O3的一种氧化铁，所以铁锈的化学反应式是

Fe+O2=Fe2O3,

配平该化学反应式。

解:设未知数p、q、r使配平的化学方程式为

pFe+qO2=rFe2O3，

比较反应物与生成物铁(Fe)和氧(O)的原子数量，由质量守恒原理，可得

Fe:p=2r;O:2q=3r。

于是，齐次线性方程组为

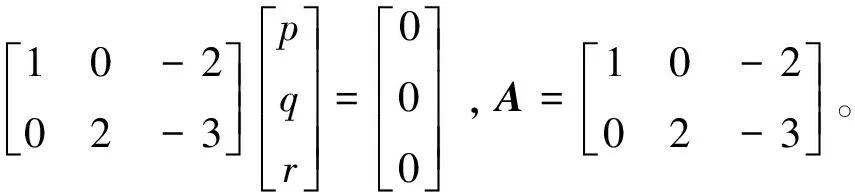
从上式可以看出，矩阵A已形成阶梯型U，其中两个主元分别是1和2，但它还不是行最简阶梯型。因为行最简阶梯型R的所有主元必须是1。于是，用第2行的一半替换第2行，即R2↔R2/2，可得

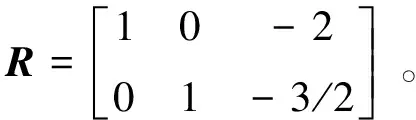
(1)

于是，Rx=0变成

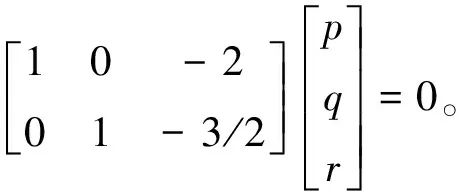
展开后，有p-2r=0或p=2r；q-3r/2=0或q=3r/2。

因此，零空间的解为

(2)

可见，解有两个轴变量p、q和1个自由变量r。若取r=1，则p=2，q=3/2。为避免出现分数，也可取r=2，从而p=4、q=3、r=2。注意到，因r是自由变量，故解(1)不唯一，即零空间的解有无限多。因此，化学方程式可配平为

2Fe+(3/2)O2=Fe2O3或4Fe+3O2=2Fe2O3。

为了让非数学专业学生看得更清楚，将化简矩阵为行最简阶梯型的步骤写的比较细，即A→R即可。下面的例子也一样。同时，为了验证方法的正确性，列举了几个经典化学反应式。

例2.2 氢氧化钠(NaOH)与硫酸(H2SO4)反应产生硫酸钠(Na2SO4)和水，即

NaOH+H2SO4→Na2SO4+H2O。

配平该化学反应式。

解:设未知数p、q、r、s满足

pNaOH+qH2SO4→rNa2SO4+sH2O

的未知变量。比较反应物和生成物中钠(Na)、氧(O)、氢(H)和硫(S)原子的数量，可得方程组:

Na:p=2r；O:p+4q=4r+s；H:p+2q=2s；S:q=r。

以标准形式重写这些方程，可得p、q、r和s的齐次线性方程组Ax=0，或表为

增广矩阵变为:

因右手边是零向量，故可对矩阵A实施操作，因为任何行变换都不会改变0。

用第1行加第3行的2倍替换第1行，即R1↔R1+2R3；用第2行加第3行的1/2倍替换第2行，即R2↔R2+R3/2。这两个变换将主元上方的所有非零元化为了零，于是得到行最简阶梯型R：

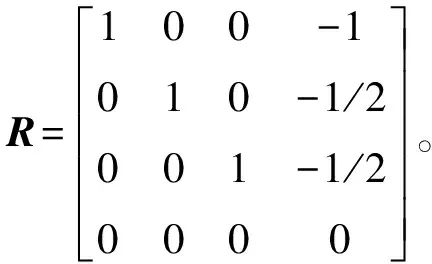
(3)

求解Ax=0简化为求解Rx=0，其中x实际上是A的零空间，它与R的零空间等价。因此，

展开后，有

p-s=0或p=s；p-s/2=0或p=s/2；r-s/2=0或r=s/2。

于是，零空间解为

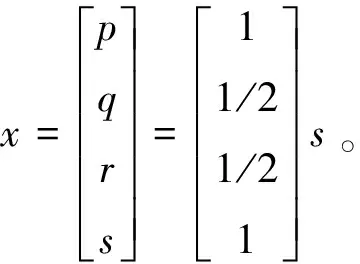
零空间解中有3个轴变量p、q、r和1个自由变量s。若取s=2，则p=2、q=1、r=1。注意到，这不是唯一解，因为有一个自由变量s，所以零空间解有无穷多。因此，化学方程式可“配平”为

2NaOH+H2SO4→Na2SO4+2H2O。

3 命令

本节利用数学软件化简矩阵为行阶梯型。正如前面的理论所预测的那样，对调行不改变行最简阶梯型的结果。这意味着，如果互换4个例子中矩阵的任何行，其行最简阶梯型都是相同的。

下例展示了Matlab软件的rref命令的特殊功效。

例3.3 配平下面的化学反应式[6]

NaCl+SO2+H2O+O2→Na2SO4+HCl。

令未知系数为p、q、r、s、t、u且满足

pNaCl+qSO2+rH2O+sO2→tNa2SO4+uHCl。

每个元素的平衡条件可写为:Na:p=2t,Cl:p=u,S:q=t,O:2q+r+2s=4t,H:2r=u。

转置后，上述方程组可写p=2t成形如Ax=0的形式，即

利用Matlab或R=rref(A)命令，Ax=0化简为Rx=0，即

取u=4，于是p=4,q=2,r=2,s=1,t=2。因此，配平的化学方程式为

4NaCl+2SO2+2H2O+O2→2Na2SO4+4HCl。

4 结 语

本文展示了如何利用行最简阶梯型来配平化学方程。实际上，只使用阶梯形矩阵仍然可以得到相同的解，但将矩阵化简为行最简阶梯型更便于推导出解。本文改进了Gabriel和Onwuka的工作，同时证明了Matlab软件的rref命令不仅可以用来输出最终结果，而且可用来验证手算结果的正确性。

[1] Gabriel C I,Onwuka G I.Balancing of Chemical Equations Using Matrix Algebra[J].Journal of Natural Sciences Research,2015 (3):29-36.

[2] Soleiman F，Stanimirovic P S.Some Matrix Iterations for Computing Generalized Inverses and Balancing Chemical Equations[J].Algorithms,2015,8(4):982-998.

[3] 古国榜,李朴编.无机化学[M].4版.北京:化学工业出版社,2015:6-25.

[4] 王萼芳,石生明.高等代数[M].5版.北京:高等教育出版社,2009:96-160.

[5] 谢彦红.线性代数及其MATLAB应用[M].北京:化学工业出版社,2014:55-64.

Method of Balancing Chemical Equations Based on Row Reduced Echelon Form

YANG Yanni

(Kashgar University， Kashgar 844006,China)

The theoretical proof of on the article [1] by using the method of matrix algebra for balancing chemical equations is given,that is,the resulting solution form null-space. Therefore,the solution may have an infinite number. In addition,the reducing matrix for ladder type of the article [1] is transformed into the row reduced echelon,and it is pointed out that the elementary row operation can be used only for reducing matrix for ladder type. It is more important that the manual operation can be replaced by using Matlab software to avoid the unnecessary trouble.

conservation of mass;chemical equation;elementary row operation;null-space;row reduced echelon form

10.3969/i.issn.1674-5403.2017.03.022

O151

A

1674-5403(2017)03-0089-05

2017-05-02

杨燕妮(1989-)，女，甘肃平凉人，在读硕士研究生,主要从事代数方面的研究.