基于FLUENT的锂电池温度场动态仿真研究

秦 凯，李 想，陈 龙

(武汉理工大学 自动化学院，湖北 武汉 430070)

基于FLUENT的锂电池温度场动态仿真研究

秦 凯，李 想，陈 龙

(武汉理工大学 自动化学院，湖北 武汉 430070)

针对电动汽车磷酸铁锂电池在高温环境下寿命短、安全性能低的问题，为了保证其工作在合适的温度范围，开展了动力电池冷却方案的动态仿真研究。运用FLUENT软件建立了电池-管道流固耦合模型，仿真计算了不同水流速度和温度对电池的冷却情况，然后运用FLUENT中UDF设置冷却管道入口水的温度，把实时电池温度作为反馈条件来控制管道中水的温度以模拟当电池温度在正常温度时采用一般水温进行冷却，当电池温度达到临界值时降低水温对电池冷却。研究表明：水的流速变化对电池冷却温度变化影响较小，水温变化对电池冷却温度变化影响较大。当电池温度达到界限时，改变管道中水的温度能够有效地控制电池的最高温度，是一种有效的冷却方案。

锂电池；动态仿真；FLUENT；冷却方案

随着新能源汽车的进一步推广和使用，锂离子电池以其高效的能量比、高电压特性及使用寿命长等诸多优点成为电动汽车电池的首选[1]。同时，动力电池对温度变化较敏感，如果锂离子电池长时间在高温环境中工作，其放电容量会相应增大，但其老化程度也会急剧增加，进而其使用寿命也会受到严重影响。当锂电池温度超过一定界限时，甚至可能会出现膨胀、泄露、爆炸的危险，严重影响日常生活和个人安全。根据文献[2]可知磷酸铁锂电池的最佳工作温度为：18℃～45℃，可接受的温差范围应不高于10℃。因此，对锂电池温度场的热分析对于推动电池在电动汽车领域的应用是十分重要的。

目前动力电池冷却技术按照冷却媒介的不同主要分为空气冷却技术、液体冷却技术和相变冷却技术[3]。液体冷却系统是指利用高热容量和导热系数的液体，通过管路将冷却液引入电池组内部，将电池热量带走。BERNARDI等[4]在假设物体内部发热均匀的基础上，提出了一种计算发热功率的模型，发热模型的来源主要是两部分，一部分是欧姆热，另一部分是化学反应热，此模型为电池生热速率模型的建立提供了基础。SATO[5]用实验的方法验证了一种电池产热功率的计算模型，并且先后应用在氢镍电池与锂离子电池上。电池内部产生的热量被分为4种热量，即焦耳热、电化学反应热、极化热及副反应热。其中，焦耳热是电池内部阻抗所产生的热量，此热量为正值；电化学反应热是电池内部化学反应所对应放出或吸收的热量，放电时为正，充电时为负；极化热是电池电极电势偏离平衡电动势而产生的能量损失，这部分热量是正值；副反应热主要是由于电池自放电、电解质分解等因素产生的热量，这部分热量始终是正值，对于锂电池来说，这部分热量很小，一般可以忽略不计。近年来，欧阳唐文等[6]将锂电池单体看作是一个发热均匀的整体获取了电池的相关参数，针对锂电池的相关特性建立了三维数学模型，并将电池的比热容和导热系数随电池的荷电状态通过分段线性插值的方式进行了有效处理，在数学模型的基础上，通过FLUENT软件建立了与之相对应的三维物理模型，对电池的温度场进行了仿真计算，在仿真计算中，分析了电池热物性参数随电池放电速率和电池温度所产生的变化对电池温度场产生的影响、电池温度场随不同放电速率所产生的变化，最终，仿真结果显示锂电池热物性参数对电池温度场分布影响较小，电池的温度上升速率随电池放电速率的增加而增加，当放电速率快时，电池内部温差也增大，同时电池冷却表面也有很大影响，冷却面越大，冷却效果越好，但是其成本也相应增加，需要综合考虑选择。张天时等[7]在原有的电池冷却结构基础之上设计了一种扁管束冷却结构，并在与电池相接触的表面添加具有高导热率的石墨，通过FLUENT仿真对比分析了没有添加石墨的电池冷却和添加了石墨的电池冷却效果，仿真结果显示，添加高导热率石墨的电池冷却结构能进一步降低电池的最高温度，电池内部的温差一致性也更小，整体提高了冷却效果。同时，设计的冷却扁管束在满足了电池冷却温度要求的基础上，相对整板冷却节省了材料，实现了轻量化。罗曼[8]通过实验模拟了电池实际发热速率，并通过有限元建立了液冷条件下的电池组散热模型，在CFX中对锂离子动力电池组和冷却液体的温度场和流场进行了仿真计算，根据仿真结果对散热结构提出了改进，经过改进的散热结构降低了电池组的最高温度并提升了电池组温度一致性。周萌[9]针对成组动力电池，分别设计了两种不同布置形式的液流换热系统，通过仿真分析和实验研究了冷却系统的换热特性。文献[2]针对电动汽车磷酸铁锂电池建立了相应的数学模型和有限元物理模型，并将物理模型导入到FLUENT中进行计算，通过设置不同的入口条件，对比分析了不同温度、不同流量下在自然环境风冷、空调强制风冷和导热油冷却3种不同情况下电池的冷却效果。JARRETT等[10]基于纯电动汽车用的高能量电池，对其进行空气散热。通过对管道的路线、长度、宽度进行不同的设计，对比分析了18种不同管道对电池的冷却效果，通过仿真结果分析得出了最有利于电池低温和温度一致性的设计，并设计了一个蛇形通道的散热板，使用FLUENT软件模拟仿真其热特性，最终分析可知合理的设计要求管道对液体压强的降低要小，入口处的管道宽度小，通过不断扩大到出口处的管道宽度就是最优设计，这样能够平衡流体的流速、传热的面积和流固耦合传热梯度，能够补偿管道所有热区的传热。TONG等[11]比较了在不同放电倍率下有水冷和没有水冷时候的电池温度分布情况，并且在有水冷的情况下水流速度越快，导热管道越薄，越能够有效地控制电池的最高温度和电池温差分布，这样在增加附加负载的同时也会增加重量和体积，这些也是综合考虑的重要因素。CHEN等[12]比较了空气冷却、液体直接冷却、液体间接冷却和散热片冷却4种不同的锂电池冷却方式,实验结果表明为达到相同的冷却效果，空气冷却相对其他冷却方式需要2～3倍的能量，同时，尽管直接冷却能够降低一点冷却温度，但间接液体冷却比直接液体冷却实践更好。HE等[13]主要研究了锂离子电池组主动温度控制和往复式水流对电池组最高温度和电池组内各单元电池温度差的影响，首先，通过实验数据建立了降阶数学模型来模拟电池热模型；然后，在此热模型的基础上，基于观测器的控制策略被用于通过控制往复式水流控制电池组的核心温度。结果显示，当控制策略用于往复式水流时能够有效地控制电池组的最高温度，也能有效地控制电池组温度的一致性，并且与被动式冷却和无方向性冷却水流相比，在电池组温度一致性上有很大提高且能够减少冷却水的用量。但上述研究中对电池冷却的仿真和实验都是在相关条件不变的情况下进行的，而实际情况可能是随着电池温度的变化，管道中水的温度和速度都会发生变化。

考虑电池生热速率随电池温度变化，通过FLUENT软件中UDF设置生热速率，首先设置不同的水流速度，观察分析不同水流速度下电池的冷却效果；然后，通过获取电池最高温度来控制电池水冷管道的入口水流的温度，使得当电池温度达到临界温度值时，通过UDF设置降低入口水流温度，当电池温度没有达到临界温度值时，通过UDF设置对应较高的水流温度；最后利用动态仿真观察电池温度场的分布，以期为冷却系统设计提供理论依据。

1 仿真模型

1.1 电池结构参数及热物性参数

处于工作状态的电池会产生焦耳热、极化热、电化学反应热和副反应热等热量，其冷却环境由电池组热管理系统控制。为降低温度场计算的复杂性，笔者采用文献[5]中方法对电池的性能参数进行计算，即导热沿x、y、z3个方向分别进行加权平均计算获得，比热容根据电池内部各物质的比热质量按质量加权法计算得到，密度简化等于电池质量与电池体积之比。单体电池结构参数及热物性参数如表1所示。

笔者采用文献[7]中的冷却结构，用铝制扁管束行程构成换热流体与动力电池间的主要传热通道，添加在电池的两侧边，具体布置形式如图1所示。

表1 单体电池结构参数及热物性参数

图1 单片电池两侧换热管束布置形式

1.2 边界计算条件

主要设置的边界有入口边界、出口边界、电池热源设置、流体接触的边界、电池流固耦合边界条件等。其中，入口边界设置相应的流体速度与温度，同时还需要计算流体的湍流强度来判断流体是层流还是紊流，湍流条件定义设置为湍流强度和水力直径。

湍流强度的计算公式为：

I=0.16Re-0.125

(1)

Re=ρfuD/v

(2)

式中：I为湍流强度；Re为管内流体雷洛数；ρf为入口流体密度；u为入口流体速度；D为入口水力直径；v为流体运动粘度。

水力直径的计算公式为：

D=4S/P

(3)

式中：S为冷却管道入口面积；P为管道入口处湿周长。

仿真模型计算中出口边界设置为自由流出outflow，将电池与外界相接触的边界设置称为绝热边界，流体湍流条件按照湍流强度计算公式和水力直径计算公式计算，管道壁面法向压力设置为零，并将电池单体与冷却管道相接触的表面设置成为流固耦合边界。

1.2.1 电池生热模型

电动汽车在行驶时，动力电池随着运行功率的大小会有不同功率的放电，电池也会随之产生热量。所以电池热源的模拟需要获取电池的生热速率，由于获取精确的电池生热速率比较困难，通常用数学模型进行描述。目前常用的是文献[4]提出的Benardi生热速率模型，其假设电池生热在电池体内均匀分布，生热速率q的估算公式为：

(4)

式中：q为电池生热速率；Vb为电池单体体积；I为充放电电流；U为电池单体电压；Uo为电池开路电压；TdUo/dT为电池的温度影响系数，与电化学反应相关的物理量。采用文献[7]中通过实验模拟出的热源，则单体锂电池在25℃，1.5C放电倍率下的生热速率为：

q=2.67×10-9t4+2.41×10-6t3-0.023t2+

36.964t+8 871.36

(5)

1.2.2 湍流模型

通过计算可知水的流速在2 m/s时，计算得此模型的雷诺数约为19 000，当雷诺数大于2 300时，流体属于湍流模型，选取k-ε低雷诺数湍流模型，关于k的输运方程为：

(6)

关于ε的输运方程为：

(7)

式中：t为时间；k为湍动能；ε为耗散率；n为壁面法向坐标；ut为湍动粘度；Gk为由速度梯度引起的湍动能的产生项；C1ε=1.44；C2ε=1.92；δk=1.0;δε=1.3。

1.2.3 电池传热模型

BERNARDI等认为锂电池内部产生的热量是均匀的。为了建立磷酸铁锂电池热特性的数学模型，需要对物理模型进行如下假设：①将电池看作是一个发热均匀的整体，并且其发热前后质量和体积都不发生变化；②电池液在电池内部流动性很小，几乎没有流动，因此假设电池内部没有流动；③实际工作中的电池温差也比较小，因此电池内部的热辐射也忽略不计；④电池内部各个部分产生的热量都是均匀的。

根据以上简化和假设，可建立磷酸铁锂电池的三维瞬态传热的数学模型为：

(8)

式中：ρ为电池密度；cp为比热容；t为温度；τ为时间；λ为导热系数;Q为电池内部单位体积的热生成率。

1.3 网格模型

笔者用GAMBIT软件建立了单体锂离子电池模型，并对电池进行了简化，去掉了电池的正负极部分。电池部分网格数为1 991 484，将电池与管道边界耦合，并画了边界层，形成了流固耦合模型，导入到FLUENT中，电池冷却网络模型如图2所示。

图2 电池冷却网格模型

2 仿真结果及分析

考虑到一般可以改变液体的种类、流速及温度，笔者仅针对液体动态的温度和流速与不变的温度和流速时分别进行对比。因此在生热速率相同的情况下，采用稳态边界条件和动态边界条件分别对电池散热进行仿真。

2.1 不同流速对电池的冷却效果

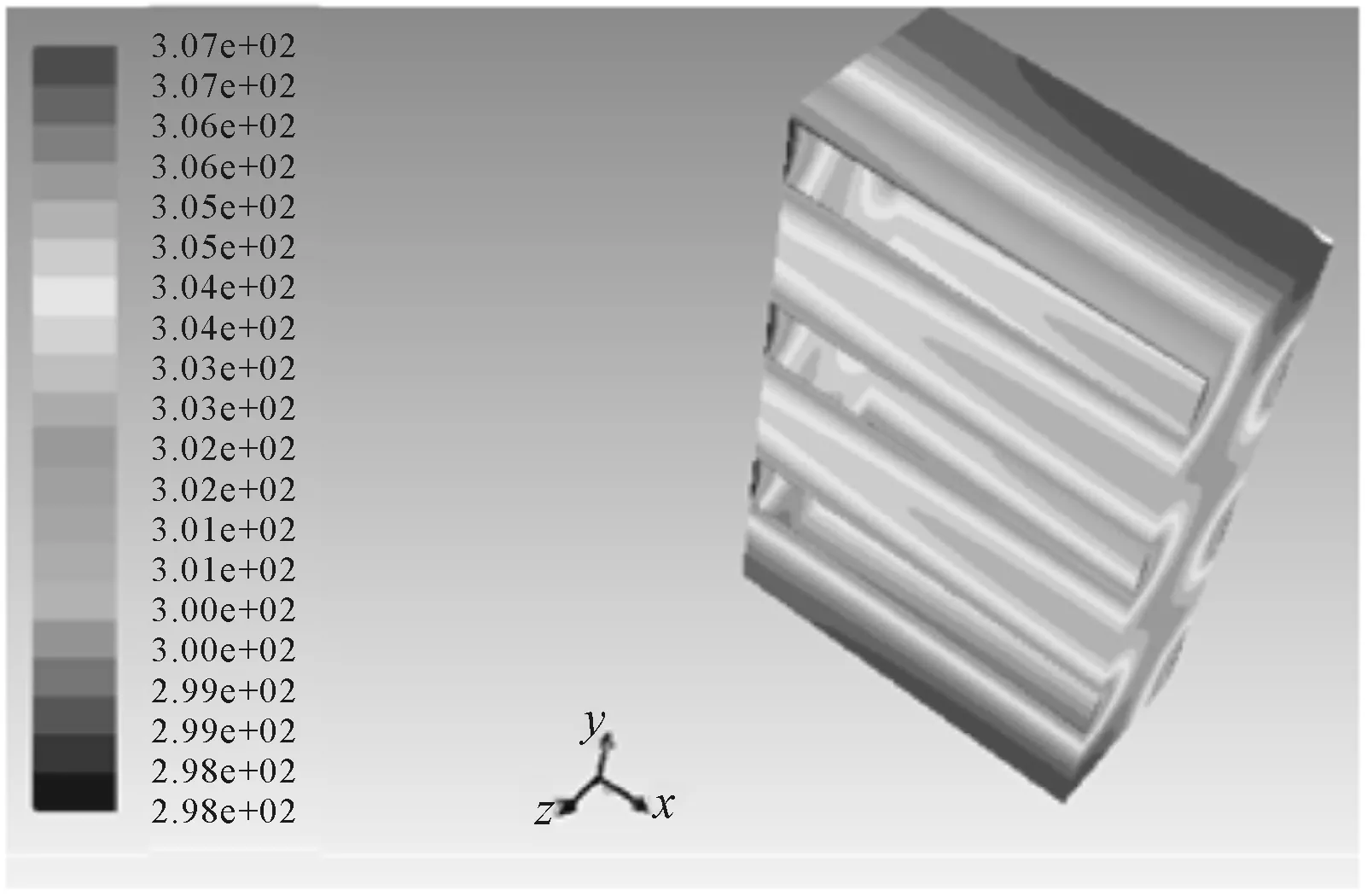
图3 V=0.2 m/s，T=298 K时电池温度场

当流速为0.2 m/s时，电池在绝热条件下，取管道中水的温度为298 K，当电池发热与管道中水冷达到平衡时，计算结果如图3所示。同理分别设置入口处水流速度为1.0 m/s和3.0 m/s时，电池冷却效果分别如图4和图5所示。

图4 V=1.0 m/s，T=298 K时电池温度场

图5 V=3.0 m/s，T=298 K时电池温度场

将以上入口不同水流速度下电池的冷却仿真结果进行总结，如表2所示。

从图3～图5及表2可以看出，在入口处最低温度相同的情况下，冷却管道入口处水流速为0.2 m/s与入口水流速为1.0 m/s及3.0 m/s时相比，电池的最高温要高出1 K,同时最大温差也要多出1 K。入口水流速为1.0 m/s和3.0 m/s时电池的最高温度及最大温差相同，说明水的流速变化对电池的冷却效果影响不大。

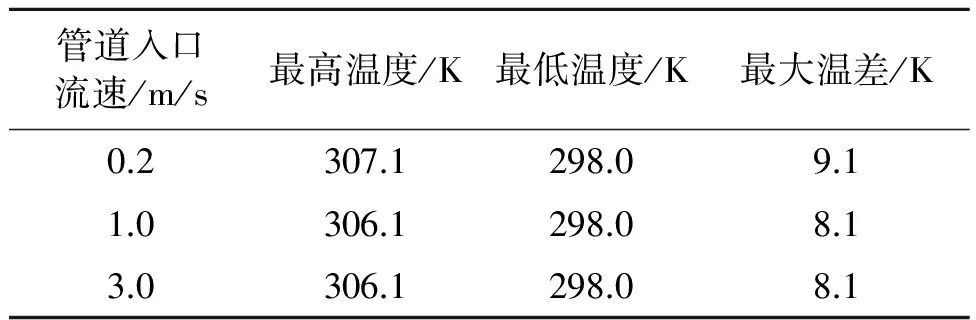
表2 不同流速下电池温度场仿真结果(T=298 K)

2.2 不同温度的冷却液对电池的冷却效果

通过FLUENT仿真可知当管道中水流的温度为310 K，流速为1.0 m/s时，电池的热场分布如图6所示。

图6 T=310 K，V=1.0 m/s时电池温度场

由图6可知：当管道中水的温度为310 K时，电池的最高温度为318 K即45℃，电池达到最适温度的临界值。为了保证动力电池的安全，给电池的最高温度设置一定的裕度5 K，设置当电池温度达到313 K即40℃为电池的最高边界温度。

当管道中水流的温度为305 K，流速为1.0 m/s时，电池的热场分布如图7所示,可知当水温为305 K即32℃时，电池温度达到313.1 K即40.1℃，达到设置的边界条件。

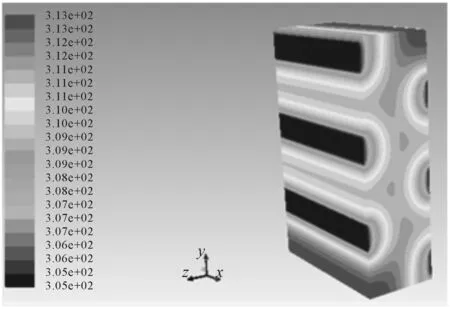
图7 T=305 K，V=1.0 m/s时电池温度场

通过以上结果，在水流速度不变的情况下，设置在电池温度没有达到313 K时，水的温度为310 K，当电池达到313 K时，调控冷却系统，使得水温降低到305 K。通过设置FLUENT中UDF来达到要求，仿真结果如图8所示。

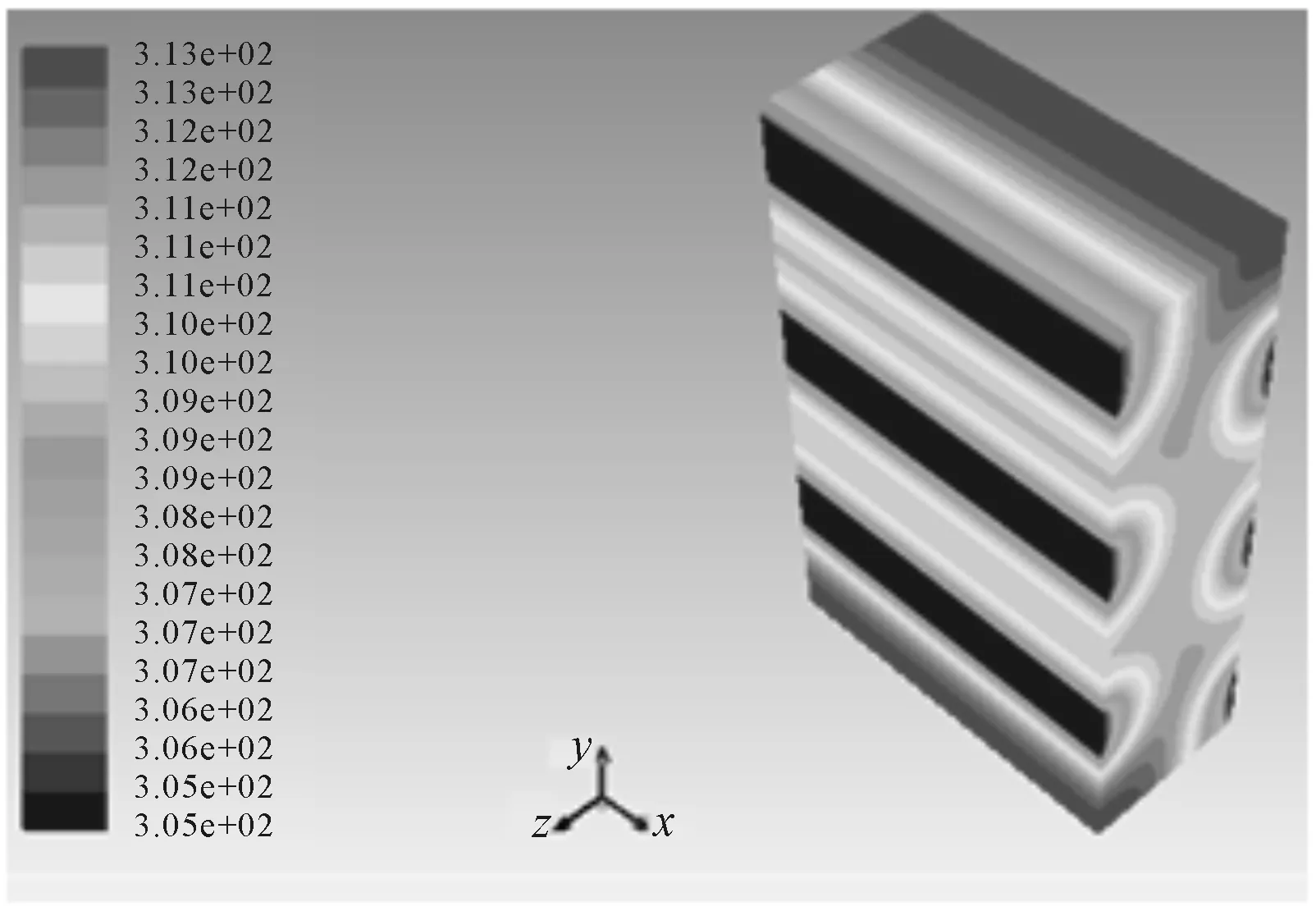
图8 动态仿真电池温度场

由图8可知，动态仿真结果能够满足电池最高温和最大温差要求，当电池温度上升，通过降低水温，可以达到冷却平衡，最终达到冷却电池的要求。电池在初始温度没有达到313 K时，管道中水的温度为310 K，当电池温度达到313 K时，管道中水的温度为305 K。最终能够保持电池最高温度为313 K。

3 结论

笔者通过对实际电池冷却分析仿真得到电池的温度分布情况，得出以下结论：①在车用锂离子电池冷却中，水流温度不变的情况下，冷却管道中不同的水流速度对电池冷却效果影响不大，因此，在车用锂离子电池冷却系统中可以适当选择较低的水流速度。②在一定水流速度下，通过仿真获得电池在接近最适边界条件下管道中水的温度，然后通过FLUENT中UDF设置当电池温度达到临界温度时降低水的温度来模拟冷却系统对电池的冷却，通过动态仿真验证了电池温度分布能够满足电池温度范围要求和电池温度要求，对于实际设计冷却系统具有重要参考意义。③笔者分析了水冷造成的影响，也可以用同样的方法动态分析风冷和其他液体对电池冷却的影响。

[1] 张遥,白杨,刘兴江.动力用锂离子电池热仿真分析[J].电源技术,2008(7):461-463.

[2] 彭影,黄瑞,俞小莉,等.电动汽车锂离子动力电池冷却方案的对比研究[J].机电工程,2015,32(4):537-543.

[3] 王小平.动力电池组热管冷却系统传热特性分析[D].长春：吉林大学,2016.

[4] BERNARDI D， PAWLIKOWSKI E, NEWMAN J. A general energy balance for battery systems[J]. Journal of the Electrochemical Society, 1985,132(1):5.

[5] SATO N. Thermal behavior analysis of lithium-ion batteries for electric and hybrid vehicles[J]. Journal of Power Source, 2001,99(1):70-77.

[6] 欧阳唐文,张兴娟,杨春信.基于CFD的锂电池温度场仿真[J].电子机械工程,2013(2):14-17.

[7] 张天时,宋东鉴,高青,等.动力电池组扁管束液流热管理增效[J].吉林大学学报(工学版),2017，47(4):1032-1039.

[8] 罗曼.纯电动汽车用锂离子电池组液体冷却散热结构分析及优化[D].重庆：重庆大学,2014.

[9] 周萌.动力电池成组液流热管理系统设计分析[D].长春：吉林大学,2014.

[10] JARRETT A, KIM I Y. Design optimization of electric vehicle battery cooling plates for thermal performance[J]. Journal of Power Sources, 2011,196(23):10359-10368.

[11] TONG W, SOMASUNDARAM K, BIRGERSSON E, et al. Numerical investigation of water cooling for a lithium-ion bipolar battery pack[J]. International Journal of Thermal Sciences, 2015(94):259-269.

[12] CHEN D, JIANG J, KIM G, et al. Comparison of different cooling methods for lithium ion battery cells[J]. Applied Thermal Engineering, 2016(94):846-854.

[13] HE F, MA L. Thermal management of batteries employing active temperature control and reciprocating cooling flow[J]. International Journal of Heat and Mass Transfer, 2015(83):164-172.

ResearchonDynamicSimulationofTemperatureFieldofLithiumBatteryBasedonFLUENT

QINKai,LIXiang,CHENLong

Aiming at the problem that lithium iron phosphate battery in electrical vehicle has a shorted life and reduced security when working at high temperature condition,in order to ensure its proper operating temperature range,a dynamic simulation of temperature field of battery based on FLUENT has been carried out. The FLUENT software was used to establish the battery-pipe fluid-solid coupling model. The cooling of the battery was calculated and analyzed at different velocity and temperature of water. Then use udf of FLUENT to get the real-time battery temperature as a feedback to control the temperature of the water in the pipelines to simulate the real situation of the cooling system of the battery.When the temperature of the battery is at normal, set the corresponding cooling temperature in the inlet of the pipe through udf. When the temperature of the battery exceeds the temperature limit,change the corresponding cooling temperature in the inlet of the pipe through udf. The results show that the change of the water flow rates has little influence on the change of the battery temperature and the change of the water temperature has a great influence on the change of the battery temperature. When the temperature of the battery reaches the limit, change the temperature of the water in the pipe can effectively control the maximum temperature of the battery. It′s an effective cooling scheme.

lithium battery；dynamic simulation； FLUENT；cooling scheme

2095-3852(2017)06-0759-06

A

2017-06-10.

秦凯(1993-)，男，湖北随州人，武汉理工大学自动化学院硕士研究生，主要研究方向为电力电子与电力传动.

TM912

10.3963/j.issn.2095-3852.2017.06.022

QINKai:Postgraduate; School of Automation, WUT, Wuhan 430070, China.