基于周期平均的固定舵双旋火箭弹控制方法

郭致远，姚晓先，张鑫

北京理工大学 宇航学院，北京 100081

基于周期平均的固定舵双旋火箭弹控制方法

郭致远，姚晓先*，张鑫

北京理工大学 宇航学院，北京 100081

对一类具有固定舵偏角的双旋弹，基于周期平均的思想推导了平均控制力幅值与执行机构电机旋转轨迹的关系，并据此提出一种使周期平均控制力幅值和方向可调的方案，分析了该方案对执行机构电机的性能要求。以双旋火箭弹为模型，通过七自由度(DOF)弹道仿真，对双旋火箭弹在该方案下的侧向修正能力、高度控制效果和落点控制效果分别进行了分析以验证该方案的可行性。结果表明:相比于在飞行过程中若干次使舵面停于所需方位的传统控制方式，基于周期平均的控制策略可以使平均控制力幅值和方向连续变化，实现固定舵双旋弹制导与控制。

周期平均；双旋；固定舵；火箭弹；制导与控制

现代战争对制导弹药的大量需求，促进了常规弹药简易制导化技术的发展。常见的改造方式是将弹箭原有引信替换为带有执行机构的制导组件[1-2]。双旋弹作为其中的一种，可以实现将鸭舵部分与弹体旋转隔离，降低了控制系统的设计成本。

国内外对于鸭式布局双旋弹的研究比较多。Costello和Peterson[3]采用线性化理论研究了双旋弹的稳定性问题，并定义了类似于传统旋转弹的陀螺稳定因子和动态稳定因子的表达式。Wernert等对双旋弹进行了系统性的研究[4-11]，在Murhpy的角运动方程[12]中引入了鸭舵的影响，修正了Costello和Peterson所推导的稳定因子的表达式。Zhu等[13]在此基础上，给出了配平攻角需要满足的稳定边界条件。Theodoulis等[8]在双旋弹七自由度动力学模型的基础上，基于鲁棒控制策略分别设计了滚转控制器和俯仰/偏航自动驾驶仪。王钰等[14]研究了双旋弹在侧向控制力作用下弹丸的落点规律。李伟和王志刚[15]研究了双旋火箭弹的动力学特性以及其稳定性条件。张冬旭[16]研究了双旋弹执行机构电机工作在电动机和发电机两种模式的优点和局限性，并基于分时分段控制思想设计了执行机构电机的控制器。许诺等[17]建立了固定舵双旋弹的角运动模型，基于非齐次角运动方程对固定舵双旋弹的角运动特性和飞行稳定性进行了分析。

然而，对于这种修正组件，常规修正方法不能提供幅值可调的控制力。目前这类修正组件多通过固定舵部分悬停于空间某一方位，来提供所需控制力或力矩，实现弹道的修正。而传统导弹控制系统设计需要执行机构可以提供大小可调的控制力，目前对于如何使具有固定舵的执行机构提供幅值连续控制力的研究并不多。文献[18]基于周期平均的思想提出了平均控制力大小可以调节的控制方法，但是并没有考虑到执行机构电机的变速过程。本文在前人的基础上，通过规划执行机构电机的运行轨迹，提出使周期平均控制力幅值可调的方案，并且基于122 mm火箭弹进行了仿真分析以验证其可行性。

1 双旋火箭弹角运动分析

相比于常规鸭式布局的双旋弹，固定舵双旋弹的执行机构结构更加简单。这种执行机构包括与弹体固联的部分和鸭舵部分，鸭舵部分带有固定舵偏角的舵片，可以相对弹体自由旋转。为了便于说明，本文使用前体(Forward Body)指代有固定舵偏角的鸭舵部分，用后体(Aft Body)指代与弹体固联部分，如图1所示。具有固定舵的双旋弹的双旋通过外转子无刷电机方式来实现，电机可以工作在发电机模式或者电动机模式[16],本文以电机工作在电动机的模式来进行分析说明。

为了便于说明，引入以下参数[19]

(1)

式中：ρ为大气密度；S为特征面积；m为弹体质量；d为弹体直径；l为弹特征长度；Iy为弹法向转动惯量；CD为弹体阻力系数；CL为弹体升力系

本文以双旋火箭弹作为研究对象，固定舵双旋弹以W=VΔ为变量的角运动方程[17,19]为

W″+H-iPW′-M+iPTW=E

(2)

式中：

图1 双旋弹执行机构示意图
Fig.1Schematic diagram of actuator of dual-spin rocket

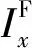
火箭弹属于低旋尾翼弹，具有静稳定性，定义双旋弹的陀螺稳定因子Sg与动态稳定因子Sd分别为

(3)

双旋火箭弹的动态稳定性条件可以表示为

(4)

从式(4)可以推导出双旋火箭弹对前体最大转速的限制条件。

2 基于周期平均的控制方案

文献[18]基于周期平均的概念提出了一种弹道修正组件以不同转速、不同振幅旋转以产生大小可控平均法向力的弹道修正方法，然而其方案并未考虑到电机的变速过程。为此，本文对其方案进行了改进。

本文作如下假设以便于简化分析过程：

2) 弹道修正组件每一时刻产生的合法向力可近似等于弹道修正组件固定在该位置时的合法向力FC。

3) 执行机构控制频率远高于弹体频率，可以采用周期平均的研究方法。

4) 执行机构电机可以控制前体相对惯性空间实现本节方案所规划的匀变速旋转运动，旋转位置指令与响应之间仅存在滞后，忽略幅值衰减。

图2 前体轨迹示意图
Fig.2 Schematic diagram of trajectory of forward body

在假设的条件下，按照半周期的情形分析。以位置A作为初始位置，开始旋转的时刻作为初始时刻，当控制力偏转到某一位置M处，假设转到M处所用的时间为t，转过的角度可以表示为

(5)

根据式(5)的终端条件，可以求得加速度大小为

(6)

(7)

(8)

用Cx、Sx来表示菲涅尔(Fresnel)函数，其定义为

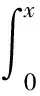
(9)

将式(7)和式(8)化简得到

(10)

(11)

通过数值计算，可以证明式(11)在0,2π内是单调递增函数。为了实现周期平均控制力幅值在0,1上的连续变化，可以求解如式(12)所列的不等式组,

(12)

数值求解式(12)可以得到φδ∈1.68,2π。根据式(6)，可以得到前体的加速度与控制角大小呈负相关的线性关系，即当控制角最小(φδ=1.68)时加速度最大。其最大值约为

(13)

对式(5)求导，可以得到

(14)

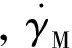
(15)

在仿真过程和实际应用中，由于式(11)反函数的解析表达式难以计算，可以使用插值的方式来替代。在这种转动方式的情况下，计算对执行机构电机的要求：

执行机构电机所需的转速

(16)

执行机构电机在所需转速下的加速性能

(17)

图3 前体限位角示意图
Fig.3Schematic diagram of limit angles of the forward body

根据几何关系及对称性，如图3所示，可以得到限位角相对于惯性空间的位置,即

(18)

式中：γδ为所需周期平均控制力FCp方向与Y轴正方向的夹角。

3 仿真分析

由于本文所述的固定舵双旋弹控制方式对电机的要求与弹的转速相关，更适宜于低速旋转弹，本文以122 mm火箭弹为例来说明。本文所述的火箭弹具有单室双推力发动机，斜置直尾翼，全程低速旋转，最大转速不超过5 r/s。助推推力使火箭弹在3 s内加速至马赫数Ma约为2.5，续航推力使火箭弹的Ma保持在2.5左右，两级推力的作用时间共14 s。火箭弹弹长为3.35 m，前体轴向转动惯量为3.5×10-4kg·m2，后体初始轴向转动惯量为0.165 kg·m2，初始法向转动惯量为64 kg·m2。火箭弹初始质量为73 kg，其中推进剂质量为37 kg。

固定舵偏角大小为5°，使用半周期控制方式，综合考虑弹体的稳定性、低通滤波特性和对执行机构电机的要求，控制半周期长取0.05 s。

火箭弹发射高度角为9°，偏航角为0°，在发射后5 s开始控制。由于火箭弹长细比较大，在仿真时加入-0.1 rad/s的初始俯仰角速度。

3.1 侧向修正能力分析

图4 仿真1和仿真2的弹道修正效果比较
Fig.4Comparison of trajectory correction effects of simulations No.1 and No.2

为说明固定舵周期平均控制与常规舵控制的异同，仿真以直接在准弹体系[20]下给出相应舵偏角指令(不考虑舵机动力学)作为对照。为了便于表示，本节将固定舵按照2节方案实现的控制称做仿真1，将直接在准弹体系下给出舵偏角的控制称做仿真2。由于火箭弹在发射后5 s开始控制，为了保证在开始控制时各弹体状态参数的一致性，在无控段给出相同的舵偏角。图4分别给出了当侧向控制指令为1°时，两种仿真条件下的射程、高度、侧偏随时间的变化曲线及两条曲线之间的偏差。

图5给出了两种仿真在准弹体系的舵偏角随时间的变化曲线。通过分析可以得出，本文提出的基于周期平均的方式在大致趋势上与常规的控制方式相似，但是由于任意时刻的总舵偏角幅值不变，对弹体姿态的影响与传统控制方式依然有所区别，因此造成仿真曲线的偏差。

为了更充分地比较两种仿真，当分别给出侧向修正舵偏角指令为δy=[-5°,-3°,-1°,0°,1°, 3°, 5°]时，固定舵双旋火箭弹的落点与对照仿真的落点如表1所列。

图5 仿真1和仿真2在准弹体系下的舵偏角比较
Fig.5 Comparison of canard deflections in quasi-body coordinate system of simulations No.1 and No.2

. .

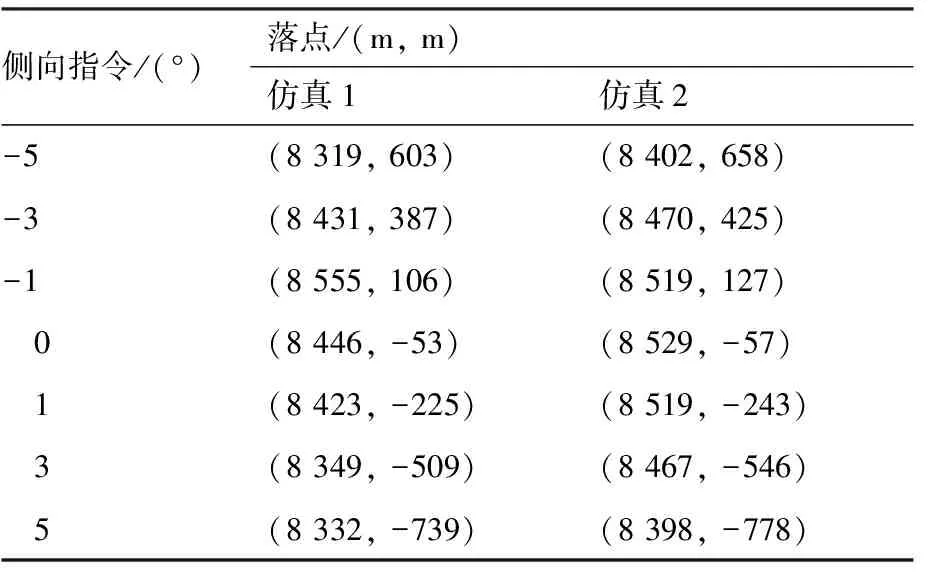
侧向指令/(°)落点/(m，m)仿真1仿真2-5(8319，603)(8402，658)-3(8431，387)(8470，425)-1(8555，106)(8519，127) 0(8446，-53)(8529，-57) 1(8423，-225)(8519，-243) 3(8349，-509)(8467，-546) 5(8332，-739)(8398，-778)

3.2 高度巡航控制

当火箭弹弹道被设计为纵向定高飞行，侧向纠偏控制时，飞行指令按照位置差通过1阶超前环节来计算。其飞行过程部分状态量如图6和图7所示。图6给出了飞行的纵向和侧向弹道，从中可以看出，固定舵双旋火箭弹可以被控制为沿着发射方向定高飞行。

图7给出了飞行过程中的舵偏角指令及舵偏角实时分解于准弹体系的分量，其中，纵向和侧向分别控制，纵向指令限制为-5°,5°，侧向指令限制为-3°,3°，若其合成幅值超出固定舵偏角大小，则控制前体停在沿着合成控制力的方向；图8给出了前体滚转角(折合在0,2π范围内)随时间的变化曲线及其部分放大图，从图中可以看出，除去由于模运算造成的突变，其曲线较为平滑，相比于文献[18]，本文所述方案更加贴合于实际情况。

图6 火箭弹纵向和侧向弹道
Fig.6 Longitude and lateral trajectory of rocket

图7 准弹体系下的舵偏角指令和实时舵偏角响应
Fig.7 Canard deflection commands and real-time canard deflection responses in quasi-body coordinate system

图9分别给出了火箭弹飞行过程中执行机构电机的转速和侧向、纵向的姿态角速度随时间的变化曲线，在整个飞行过程中，姿态角速度并没有发散的趋势，弹体是稳定的。

图8 前体滚转角变化曲线及其局部放大图
Fig.8Variation curve of rolling angle of forward body and its detail view

图9执行机构电机转速和火箭弹的纵向/侧向姿态 角速度变化曲线
Fig.9 Variation curves of motor of actuator and longitude/lateral attitude angular velocities of rocket

3.3 蒙特卡罗分析

火箭弹按照如下方式制导：在5 s内，火箭弹处于无控阶段；在5～15 s，火箭弹处于平飞控制阶段；在15 s以后，火箭弹处于末制导阶段。纵向制导指令按照式(19)以高度形式给出，侧向始终保持纠偏控制。

hcom=

(19)

式中：dx为火箭弹与目标的距离沿x轴的分量；dxterm为在15 s时火箭弹与目标的距离沿x轴的分量；hcom为高度指令。考虑的扰动因素包含炮口初始扰动和随机风，并假设这些扰动均服从正态分布，如表2所示。

表2 扰动因素分布参数Table 2 Distribution parameters of disturbance factors

图10 蒙特卡罗仿真的落点分布
Fig.10Distribution of drop points of Monte Carlo simulation

4 结 论

1) 针对固定舵双旋式执行机构不能提供幅值可调的控制力的问题，据此提出一种使周期平均控制力幅值和方向可调的方案，分析了该方案对执行机构电机的性能要求。

2) 仿真结果表明，固定舵的周期平均控制策略可以有效地解决固定舵双旋弹在常规控制策略下控制力幅值不可连续变化的问题。

通过对执行机构电机的性能要求分析可以看出，本文所述的控制策略受到弹体转速的制约。此外，由于火箭弹前体始终处于较大角加速度的运动中，执行机构电机消耗的能量较大，对执行机构电机的设计要求较高。

[1] REGAN F J, SMITH J. Aeroballistics of a terminally corrected spinning projectile (TCSP)[J]. Journal of Spacecraft and Rockets, 1975, 12(12): 733-738.

[2] GAGNON E, LAUZON M. Low cost guidance and control solution for in-service unguided 155 mm artillery shell: DRDC Valcartier TR 2008-333[R]. Quebec: Defence Research and Development Canada, 2009.

[3] COSTELLO M, PETERSON A. Linear theory of a dual-spin projectile in atmospheric flight[J]. Journal of Guidance, Control, and Dynamics, 2000, 23(5): 789-797.

[4] WERNERT P, LEOPOLD F, LEHMANN L, et al. Wind tunnel tests and open-loop trajectory simulations for a 155 mm canards guided spin stabilized projectile[C]∥AIAA Atmospheric Flight Mechanics Conference and Exhibit. Reston, VA: AIAA, 2008: 1-17.

[5] THEODOULIS S, MOREL Y, WERNERT P. Trajectory-based accurate linearization of the 155mm spin-stabilized projectile dynamics[C]∥AIAA Modeling and Simulation Technologies Conference. Reston, VA: AIAA, 2009: 1-21.

[6] WERNERT P. Stability analysis for canard guided dual-spin stabilized projectiles[C]∥AIAA Atmospheric Flight Mechanics Conference. Reston, VA: AIAA, 2009: 1-24.

[7] SPAGNI J, THEODOULIS S, WERNERT P. Flight control for a class of 155 mm spin-stabilized projectile with reciprocating canards[C]∥AIAA Guidance, Navigation, and Control Conference. Reston, VA: AIAA, 2012: 1-24.

[8] THEODOULIS S, GASSMANN V, BRUNNER T, et al. Robust bank-to-turn autopilot design for a class of 155mm spin-stabilized canard-guided projectiles[C]∥AIAA Atmospheric Flight Mechanics(AFM) Conference. Reston, VA: AIAA, 2013: 1-24.

[9] THEODOULIS S, GASSMANN V, WERNERT P, et al. Guidance and control design for a class of spin-stabilized fin-controlled projectiles[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(2): 517-531.

[10] SÉVE F, THEODOULIS S, WERNERT P, et al. Pitch/yaw channels control design for a 155mm projectile with rotating canards, using aH∞loop-shaping design proce-dure[C]∥AIAA Guidance, Navigation, and Control Conference. Reston, VA: AIAA, 2014: 1-24.

[11] THEODOULIS S, SÉVE F, WERNERT P. Robust gain-scheduled autopilot design for spin-stabilized projectiles with a course-correction fuze[J]. Aerospace Science and Technology, 2015, 42: 477-489.

[12] MURPHY C H. Symmetric missile dynamic instabilities[J]. Journal of Guidance, Control, and Dynamics, 1981, 4(5): 464-471.

[13] ZHU D L, TANG S J, GUO J, et al. Flight stability of a dual-spin projectile with canards[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2015, 229(4): 703-716.

[14] 王钰, 王晓鸣, 程杰, 等. 基于等效力方法的双旋弹侧向控制力落点响应分析[J]. 兵工学报, 2016, 37(8): 1379-1387.

WANG Y, WANG X M, CHEN J, et al. Analysis on impact point response of a dual-spin projectile with lateral force based on equivalent force method[J]. Acta Armamentarii, 2016, 37(8): 1379-1387 (in Chinese).

[15] 李伟, 王志刚. 双旋制导火箭弹运动特性分析[J]. 固体火箭技术, 2014, 37(2): 143-149.

LI W, WANG Z G. Analysis of motion characteristics for dual-spin projectile[J]. Journal of Solid Rocket Technology, 2014, 37(2): 143-149 (in Chinese).

[16] 张冬旭. 可控滚转二维弹道修正机构的研究[D]. 北京: 北京理工大学, 2015: 71-96.

ZHANG D X. Research on the rolling controlled two-dimensional trajectory correction mechanism[D]. Beijing: Beijing Institute of Technology, 2015: 71-96 (in Chinese).

[17] 许诺, 于剑桥, 王亚飞, 等. 固定翼双旋弹动力学特性分析[J]. 兵工学报, 2015, 36(4): 602-609.

XU N, YU J Q, WANG Y F, et al. Analysis of dynamic characteristics of fixed-wing dual-spin projectiles[J]. Acta Armamentarii, 2015, 36(4): 602-609 (in Chinese).

[18] 许诺, 于剑桥, 王亚飞. 基于周期平均的固定翼双旋弹弹道修正方法[J]. 航空学报, 2015, 36(9): 2892-2899.

XU N, YU J Q, WANG Y F. Trajectory correcting method of fixed-canard dual-spin projectiles based on period average[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(9): 2892-2899 (in Chinese).

[19] 韩子鹏. 弹箭外弹道学[M]. 北京： 北京理工大学出版社, 2014: 145-270.

HAN Z P. Exterior ballistics of projectiles and rockets[M]. Beijing: Beijing Institute of Technology Press, 2008: 145-270 (in Chinese).

[20] 钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学[M]. 北京： 北京理工大学出版社, 2008: 29-55.

QIAN X F, LIN R X, ZHAO Y N. Missile flight mechanics[M]. Beijing: Beijing Institute of Technology Press, 2008: 29-55 (in Chinese).

Controlmethodforaclassoffixed-canarddual-spinrocketsbasedonperiodaverage

GUOZhiyuan,YAOXiaoxian*,ZHANGXin

SchoolofAerospaceEngineering,BeijingInstituteofTechnology,Beijing100081,China

Acontrolmethodforaclassoffixed-canarddual-spinrocketsisproposedtoadjustthemagnitudeandthedirectionoftheaveragecontrolforce.Themethodispresentedaccordingtotherelationshipbetweenthemagnitudeoftheaveragecontrolforceandthespinningtrajectoryoftheactuatormotor.Thisrelationshipiscalculatedbasedontheideaoftheperiodaverage.Basedonasimulationof7DegreesofFreedom(DOF)trajectory,thelateralcorrectionabilityandtheeffectsoftheheightcontrolandthedroppointcontrolofthefixed-canarddual-spinrocketareanalyzedtoverifythefeasibilityofthecontrolmethodproposed.Theresultsshowthatincontrasttothetraditionalcontrolmethodofholdingthecanardtothedirectionneededseveraltimesduringtheflight,thecontrolmethodbasedontheperiodaveragecancontinuouslyadjustthemagnitudeandthedirectionoftheaveragecontrolforce,soastorealizetheguidanceandcontrolofthefixed-canarddual-spinrocket.

periodaverage;dual-spin;fixed-canard;rocket;guidanceandcontrol

2017-04-06；

2017-06-14；

2017-08-02；Publishedonline2017-08-071537

URL：http://hkxb.buaa.edu.cn/CN/html/20171224.html

.E-mailyxx11@bit.edu.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.321307

2017-04-06；退修日期2017-06-14；录用日期2017-08-02；网络出版时间2017-08-071537

http://hkxb.buaa.edu.cn/CN/html/20171224.html

.E-mailyxx11@bit.edu.cn

郭致远，姚晓先，张鑫．基于周期平均的固定舵双旋火箭弹控制方法J． 航空学报,2017,38(12):321307.GUOZY,YAOXX,ZHANGX.Controlmethodforaclassoffixed-canarddual-spinrocketsbasedonperiodaverageJ.ActaAeronauticaetAstronauticaSinica,2017,38(12):321307.

V249.12;TJ765.1

A

1000-6893(2017)12-321307-08

苏磊, 李丹)