基于五孔探针的大S弯进气道旋流畸变评估

徐诸霖，达兴亚，范召林

中国空气动力研究与发展中心 高速空气动力研究所，绵阳 621000

基于五孔探针的大S弯进气道旋流畸变评估

徐诸霖，达兴亚*，范召林

中国空气动力研究与发展中心 高速空气动力研究所，绵阳 621000

背负式S弯进气道拥有较好的前向雷达隐身性能，同时有利于起落架布置、武器内埋，但其出口流场的非均匀性会严重影响发动机的稳定性。除了总压畸变、总温畸变的影响之外，旋流畸变也是流场非均匀性的一种重要体现。为研究背负式大S弯进气道的旋流畸变特性，采用美国汽车工程师协会(SAE)的旋流评估方法，利用基于五孔探针的旋转式测量段对进气道出口的强旋流场进行测量分析，入口马赫数的范围为0.2～0.6。所有马赫数下旋流方向(Swirl Directivity, SD)和旋流对数(Swirl Pairs, SP)变化不大，均显示出口旋流为对旋模式，与理论分析和数值计算结果吻合。同时，测量的对旋涡呈现出弱非对称性，最大旋流角超过40°，旋流强度(Swirl Intensity, SI)从内环的6°增加到外环的13°左右，且在马赫数小于0.5的范围内没有明显变化。本文研究表明，虽然SAE的旋流畸变计算方法中部分指标可以有效识别出大S弯进气道的旋流模式，但是旋流强度指标却明显不能表现出对旋涡的强旋状态，制约了其在该类进气道/发动机相容性评估中的应用。

S弯进气道;五孔探针;旋涡;分离流动;旋流畸变

随着S弯进气道的普及应用，与旋流相关的进气道/发动机相容性问题越来越突出，比如使用大S弯进气道的无人机[1-2]、具有边界层吸入式进气道的N+3代客机[3]。影响发动机稳定的因素除了旋流强度之外还有旋流方向：与发动机转动方向相反的旋流会引起发动机失速、喘振[4]，严重时甚至导致发动机空中停车[5]；正向旋流将影响发动机的推力效率，使耗油率上升[6]。长期处于对涡旋流中的发动机极易出现高循环疲劳失效[7]。

旋流是一种典型的横向分离流动，其产生与进气道内部的二次流动和分离涡密切相关，而这两者是由于气流通过弯道时的离心压力梯度所导致的[8]，而大S弯进气道具有更大的弯度，其离心压力梯度会更大，因此其出口旋流强度会显著增大。美国汽车工程师协会(Society of Automotive Engineers，SAE)总结了旋流的类型、产生及其影响和旋流评估等问题，发布了旋流评估指南Aerospace Information Report 5686 (AIR 5686)[8]。Honeywell发动机公司的Sheoran等[9]发现整体涡对压气机的影响大于对涡和局部涡，但是对涡对压气机流量、效率、总压比也有削弱，当其存在时，发动机稳定工作范围降到只有原来的2/3[10]。

国内对S弯进气道也有一定程度的研究。张晓飞等[11]发现水平飞行状态下的S弯进气道也存在对涡旋流，且结构不随攻角变化；侧滑状态下，对涡旋流逐渐演变为整体涡且旋流强度较大，极易引发发动机喘振或者熄火。谢文忠和郭荣伟[12]研究了位于腹下且无隔道的跨声速大偏距S弯进气道，发现进气道第二拐点处的对涡导致了进气道出口截面总压畸变区域偏大，飞行攻角和侧滑角对进气道总压恢复系数的影响不大。叶飞等[13]设计了一种可调叶片式旋流发生器，模拟了偏置对涡旋流，发现随着旋流向下游发展，在旋流诱导速度的作用下，2个旋流中心会按照较强旋流的方向产生偏转。目前，对畸变的控制技术主要有主动与被动2种。主动控制技术以射流控制为主，例如刘雷等[14]对进气道附面层进行小角度吹气模拟，发现在流动分离处前方第一个拐点吹气对旋流畸变强度有一定程度的减弱；被动控制技术以扰流片控制为主，例如李大伟和马东立[15]通过在进气道安装小型导流叶片降低了S弯进气道的总压畸变指数，且对总压恢复系数影响极小。

总的来说，旋流对发动机的影响问题已经得到国内外的广泛重视。但是，旋流对下游发动机的影响却一直是理论研究与试验研究的难题，一方面是由于旋流测量和模拟的难度，另一方面则是发动机对进气道旋流场的影响要远大于总压畸变,也即发动机可能会改变旋流特性。因此，开展单独进气道的旋流畸变研究，是进气道/发动机相容性评估、发动机与旋流之间的相互作用分析的重要基础。

本文针对某背负式大S弯进气道，首先通过计算流体动力学(Computational Fluid Dynamics， CFD)方法对大S弯进气道旋流场进行模拟分析，再采用基于五孔探针的测量段和SAE旋流畸变评估方法，对进气道出口截面的旋流进行了测量与评定。通过对比试验与计算2种结果来分析旋流模式、强度与来流之间的关系，加深对进气道出口流场旋流畸变的认识，进而为旋流畸变对背负式大S弯进气道/发动机相容性影响的评估奠定基础。

1 旋流测量方法

1.1 大S弯进气道模型和试验方法

图1 进气道在飞翼模型中的安装位置
Fig.1 Installation position of inlet in flying-wing model

1.2 大S弯进气道测量段面临的问题

传统进气道试验使用固定的总压测量耙测量出口截面的总压分布，一般在周向分布6耙、8耙或者12耙，每个耙上安装5个皮托管式总压探针，耙间相对位置比较固定，所以测得的数据表现出来的规律不具有较强的连续性，因此，常常需要增加测试工作量来提高数据的连续性[17]。这种方法适用于流向角不大的情况，当流向角增大后，可以使用Kiel探针或者五孔探针，其中Kiel探针不能测量流向角，只能测量总压。由于进气道出口流场沿周向变化剧烈，当测量耙间隔过大时有可能不能分辨出真实的畸变图谱，进而影响畸变的评估结果。因此，本文采用基于五孔探针的旋转测量段。

1.3 五孔探针测量段结构设计

图2 五孔探针测量段示意图
Fig.2Schematic of five-hole probe measurement section

五孔探针测量段如图2所示。探针由测量段的外壁面嵌入进气道出口流场中，受探针制造、校准等诸多因素的影响，在周向仅安装了3个L型五孔探针，彼此间隔为120°。探针尾部与轴向步进电机连接，由电机自动控制其径向移动。在轴向电机上集成了相对编码器，配合专用的电机驱动器，使步长达到了0.007 9 mm。测量段的周向转动采用的是手动方式，探针会随着测量段一起转动，从而实现任意周向站位的测量。

1.4 测量位置

根据美国SAE的总压测量规范，在径向等面积中心布置5个测量点，周向测量角度间隔10°，总共测点数为180个，如图3所示。在图3中，从外向内依次标识为环1～环5，底部位置的周向角(θ)标识为0°，并沿顺时针方向递增。由于探针为120°等间隔分布，因而只需要13个周向测量角度便可以测得整个扇面的数据。

图3 测量点位置
Fig.3 Positions of measurement points

1.5 五孔探针参数及数据处理方法

所使用的3个L型五孔探针为美国Aeroprobe公司的产品。如图4所示，探针头部为圆锥形，轴的长度为152.4 mm、直径为4.8 mm，头部长25.4 mm、直径为3.18 mm，尾部的5根测压管连接到压力扫描阀的测压端口。该探针由Aeroprobe公司校准，校准马赫数为0.1～1.5，流向角精度为0.4°，速度精度为0.8%，气流测量角为60°[18]。

图4 五孔探针参数
Fig.4 Parameters of five-hole probe

图5 两种方法的处理结果(位置：环4，θ=170°)
Fig.5Results of two methods (position: Ring 4, θ=170°)

采用五孔探针测量复杂流场时，压力信号从毛细管引出，需要一定稳压时间，所以在测量脉动流场时会受到一定影响。本文分析了2种数据处理方法对结果的影响，如图5所示，其中：图5(a)为采用局部最小二乘(Local-Least Squares，LLS)拟合方法的结果，图5(b)为采用分区拟合(Sector Fitting，SF)方法的结果。LLS方法是Aeroprobe推荐的数据处理方法，其优点是精度高，但处理速度慢。SF方法使用探针压力测值最大的点确定一个分区，读取对应分区的拟合系数，再进行快速拟合[19-20]，虽然精度稍低，但处理速度更快。如图5所示，LLS方法几乎在所有的点都能处理出结果，但是压力波动十分剧烈，使得这些值失去了统计意义。相反，SF方法具有更好的处理结果，除少数点返回0外，其余点的波动量显著减小，且有效数据点较多。

2 旋流的定义和计算方法

2.1 旋流角的定义

考虑到不同因素的影响，例如物理参数、进气道构造、旋流特征等，进气道旋流可以分为4种[8]：整体涡旋流(Bulk Swirl)、对涡旋流(Paired Swirl)、横向涡旋流(Cross-Flow Swirl)、集中涡旋流(Tightly-Wound Swirl)。集中涡旋流一般产生于当进气道在地表或近地面吸入地表的旋涡之后，而横向涡旋流大多在涡桨发动机进气道中产生。整体涡旋流与对涡旋流普遍出现于当今绝大多数现役战机进气道之中，本文所研究的大S弯进气道中的旋流即为对涡旋流，为了区分不同旋流模式和构建相关旋流指标，本文引入旋流角α这一参数。α为出口截面上周向速度Uθ与轴向速度Ux的夹角，具体表达式为

(1)

本文规定从进气道出口往入口看，逆时针为正向。

2.2 旋流畸变指标

本文使用 AIR 5686[8]标准规定中对旋流畸变参数的定义和旋流指标体系，基于环面定义以下4种旋流指标：

(2)

(3)

2) 旋流强度(Swirl Intensity，SI)。旋流强度为绝对周向旋流角的加权平均值，且不具有方向性，其表达式为

(4)

3) 旋流方向(Swirl Directivity，SD)。旋流方向表示对涡中主导旋流的旋转方向，其表达式为

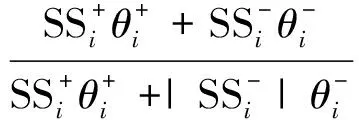
(5)

其值正负代表了对涡整体旋向，其值大小代表了旋流与风扇/压气机转向的拟合程度,范围为-1～+1：当其值为+1时，出口截面存在唯一与压气机转向一致的正向整体涡旋流；当其值为-1时，出口截面存在唯一与压气机转向相反的负向整体涡旋流；当其值介于-1和+1之间时，出口截面存在对涡。

4) 旋流对数(Swirl Pairs，SP)。旋流对数表示出口截面所存在对涡数目，其表达式为

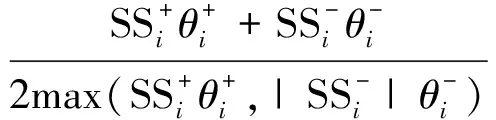
(6)

针对单对涡旋流来说，当SP的值为+1时，表示存在1对对称对涡；当其值介于+0.5与+1之间时，表示存在1对非对称对涡；当其值为+0.5时，表示存在单个正/负旋向的整体涡；对于复杂的旋流状态，SP值是没有上限的，例如SP=2时，代表2对对涡。图6为风扇/压气机旋转方向为逆时针且只存在1个对涡时的SP、SD示意图[8]。

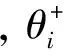
上述4项旋流畸变指数均适用于不同旋流类型，对比以前所使用的旋流畸变指数SC(60)等，更能全面描述旋流畸变模式[21-22]。

图6 SP、SD示意图
Fig.6 Schematic of SP and SD

图7 单对对称涡旋流第i环旋流角分布
Fig.7Swirl angle of the ith ring of symmetric single paired swirl

3 旋流畸变分析

3.1 进气道旋流演变分析

首先借助CFD计算结果对管内流动进行分析。虽然CFD在模拟大S弯进气道强分离流方面还存在一些不足，但可为认清基本流动状态提供依据，也可以为试验提供参考。

计算域包含入口等直段、进气道和出口等直段，计算网格约780万，选用Spalart-Allmaras模型，入口给定总温、总压边界条件，出口给定流量边界条件，雷诺数取试验值。图8给出了计算得到的马赫数Ma=0.5时的进气道轴向剖面的总压恢复系数和流线分布，其中pt0为入口总压，p0为当地总压，轴向X=625 mm截面为进气道出口截面，X=0 mm截面为进气道入口截面。其他马赫数下的畸变图谱和流线分布与图8十分类似，本文不再给出。从图8中可以看出，出口截面上部具有一个较大的分离区。

图8 进气道总压恢复系数和流线分布(Ma=0.5)
Fig.8Distributions of total pressure recovery coefficient and streamline of inlet (Ma=0.5)

图9 内部截面总压恢复系数和旋流分布(Ma=0.5)
Fig.9Distributions of total pressure recovery coefficient and swirl of internal sections (Ma=0.5)

图9展示了大S弯进气道8个剖面上的总压恢复系数和旋流分布。可以看出，从入口至出口，管道剖面形状从半椭圆形演变为直径为250 mm的圆形。X=0，89 mm时，截面位于进气道第1个弯道区域，气流随着弯道均匀地向下流动，并未出现旋涡。当X=179 mm时，截面下方两侧出现较小的圆形低压区，而此时并没有旋涡形成，但当X=268 mm时，截面位于大S弯进气道最大偏移截面，同时也是第1个弯道的末端、第2个弯道的始端，截面左、右下角出现旋涡。当气流进入第2个弯道时，两侧旋涡逐渐耗散，而上部流动分离区增大，总压恢复系数下降到0.82，为全流道最低数值。在进气道后半段，上部较大低压区与下部两侧较小低压区的作用范围不断扩大，但总压恢复系数逐渐提高，同时在上部低压区形成较大的对涡。因此，上半部的旋流应是试验测量的重点。

3.2 旋流角测量结果与计算结果的对比分析

图10给出了Ma=0.5时试验和计算得到的旋流角云图与速度矢量图。两种结果相同点表现为：旋流角都呈现出水平反对称分布，上半截面都存在较强的对涡且两侧旋流角最大值的绝对值均超过了40°；下半截面旋流角在±10°以内且两侧均存在小范围旋流角激增区，速度在此区域有所波动，但并未形成涡流。不同点表现为：计算结果对涡分布是均匀对称的，而试验结果中右侧涡作用范围略大于左侧涡，右侧大旋流角区域也大于左侧。值得注意的是，计算结果在上半截面靠近中心的区域预测到一对反对称旋流角激增区，这一区域对应着涡的反向回流，而试验旋流角云图中并不能明显看出这一回流区，说明试验中这一区域的旋流角较小。比较试验和计算相同测点的速度矢量，可以看出，试验中的对涡区域向左偏置，计算中的对涡区域对称性很好，两者反映出的对涡旋向是一致的，从而得出：计算结果对于对涡位置的大旋流角区域的预测是比较准确的，但是并没有反映出回流区旋流角的真实大小。

图10 出口截面旋流角和速度矢量的分布(Ma=0.5)
Fig.10Distributions of swirl angle and velocity vector on outlet section (Ma=0.5)

对于对涡旋流呈现非对称分布问题，麻省理工学院Tournier[23]曾发现大S弯进气道的分离拓扑呈现出弱不对称性，并指出这是由于真实流场中对称结构的不稳定性引起的。Tournier使用的8耙总压测量段测得的非对称性并不明显，这与文献[16]中12耙总压测量段测得的弱不对称总压图谱类似。由于实际的弱不对称性并不是简单的图谱周向平移或者错位，所以可以排除探针测量位置不对称的因素。文献[13]中提到在进气道入口设置偏置的对涡旋流，随着气流向下游发展，在旋流诱导速度的作用下，2个旋流中心会按照较强旋流的方向产生偏转，而来流在入口截面的周向速度分量决定了入口旋流是否偏置，所以入口气流的均匀性也可能是引发出口截面对涡不对称的诱因之一。所以本文推断这种旋流不对称性与分离拓扑的微弱不对称性有关，而进气道结构加工中存在的微小误差和来流的不均匀性可能是触发流动不稳定、诱导非对称分离拓扑的主要原因。

图11是试验测量的其他马赫数下出口截面的旋流角分布云图和速度矢量图。大体上，各马赫数下旋流角云图均表现出一致的规律：呈现出具有弱不对称性的八字分布，上半面旋流角大于下半面，右面大旋流角区域略大于左面。从而得出，在中低亚声速流动中，马赫数对旋流角的影响是很有限的。

图11 不同马赫数下出口截面的旋流角和速度矢量分布
Fig.11 Distributions of swirl angle and velocity vector on outlet section at different Mach numbers

图12 各环旋流角曲线(Ma=0.5)
Fig.12 Curve of swirl angle of each ring (Ma=0.5)

图12为马赫数为0.5时，出口截面的各环旋流角变化曲线，横坐标为0°～360°。与图3不同的是，图12的0°起点在出口截面的正上方(图3中的180°位置)，角度递增方向为顺时针。数值上，各环曲线从0°到360°大致处于下降趋势。最内环变化最平稳，由内到外，振荡幅度逐渐增大，在最外环的300°和50°方位，幅值从10°陡增到接近40°的峰值。最大峰值一般出现在20°和340°方位，为大低压区的对涡区域；最小值出现在周向180°附近，其幅值为0°，曲线数值符合反对称规律。

3.3 旋流模式分析

图13为在不同马赫数下各环旋流方向SD的分布。从图中可以看出，无论马赫数在0.2～0.6之间如何变化，对涡总体方向为正向，从外到内，旋向呈现由一般到弱、再到强的正向旋流变化趋势，其中环3的旋流表现出最弱的同向性，SD平均值只有0.125 4，环5呈现最大占比的正向旋流，平均SD值达到0.275 4，而且从环4到环5，正旋程度增幅达到88.6%。

图13 不同马赫数下SD分布图
Fig.13 Distributions of SD at different Mach numbers

图14 不同马赫数下SP分布图
Fig.14 Distributions of SP at different Mach numbers

图14为在不同马赫数下各环旋流对数SP的分布。SP的值代表出口截面上对涡的个数，从Ma=0.2到Ma=0.6，各环SP均未超过1，所以出口状态为单对涡旋流。另外，环3的平均SP值最大，表明该环对涡对称性较好；环5的平均SP值最小，其值只有0.78，表明该环对涡对称性较差。对比图13与图14可知，由于SP与SD两者之间存在一定的反比关系，因而所表现出来的特征规律是一致的，即对涡中2个子涡旋向相互抵消程度越大(SD趋于0)，对称性越好(SP趋于1)。改变马赫数，各环SP值变化幅度的平均值在1.7%左右，综合SD值的变化可以得出：来流速度对各环对涡的旋向与对数影响也不明显。

3.4 旋流强度分析

图15 不同马赫数下SS分布图
Fig.15 Distributions of SS at different Mach numbers

图15为在不同马赫数下各环平均旋流角SS的分布。可以看出，在马赫数不变的条件下，正负平均旋流角从外向内，其绝对值逐渐减小，但正平均旋流角绝对值始终大于负平均旋流角绝对值。增大马赫数，各环正负平均旋流角表现出先减小后增大的趋势。马赫数为0.6时，各环正平均旋流角的平均值最大为12.41°，各环负平均旋流角的平均值的绝对值最大为9.61°。所以，平均旋流角变化的幅度与入口马赫数的关系也不大。

图16为在不同马赫数下各环旋流强度SI的分布。SI绝对值大小反映了旋流畸变剧烈程度。5种马赫数状态表现出的趋势相似，从内环到外环旋流强度逐级增大，最外环平均旋流强度为12.9°，超过最内环的2倍。可以看出，在马赫数小于0.5的范围内SI基本保持不变，而马赫数为0.6时SI有稍微明显的变化。但是，SI仅仅只是代表一个平均程度，对于超过±15°的旋流角来说，各环的差异是很大的，所以该旋流强度指数并没有反映该进气道旋流的真实强度，表明该指标并不能完全表征对旋涡的强旋流状态。

图16 不同马赫数下SI分布图
Fig.16 Distributions of SI at different Mach numbers

4 结 论

本文对某大S弯进气道的旋流流场进行了测量与分析，明确了旋流畸变特性，结论如下：

1) 该进气道的旋流为对旋模式，且各环为单对涡旋流，大旋流角主要集中在上半部分，外环的旋流角达到近40°，旋流强度超过12°，旋流强度由外环至内环逐渐减弱。

2) 研究范围内，入口马赫数与进气道出口旋流畸变形式以及分布规律的相关性较弱，对畸变角度和强度的影响不大，所以马赫数对该进气道分离涡形态的影响也不大。

3) 相比传统12耙总压测量段测得的总压畸变图谱所呈现的对称性，五孔探针测量段在进行周向加密之后测量的旋流场却呈现出弱非对称性，正向旋涡占据更大区域，且强度也大于反向旋涡。

4) 该进气道的非对称旋流的成因可能与流动不稳定性、入口均匀性、模具精度等因素有关，但需进一步的试验与验证。

5) SAE方法能够准确判断出进气道的对旋畸变模式，但畸变强度指标却不能表现出对旋涡的强旋流状态，可能会影响其在相容性评估中的应用。

[1] JIRASEK A. Evaluation of the vortex generator flow control in the FOI-EIC-01 inlet at different flight conditions: AIAA-2007-5065[R]. Reston,VA: AIAA, 2007.

[2] JIRASEK A. Example of integrated CFD and experimental studies: Design of flow control in the FOI-EIC-01 inlet[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2009, 223(4): 369-377.

[3] TOURNIER S E. Flow analysis and control in a transonic inlet: AIAA-2005-4734[R]. Reston, VA: AIAA, 2005.

[4] LUDWIG G R. Case studies on effect of inlet swirl on engine operability[R]. Warrendale, PA: SAE International, 1993.

[5] AULEHLA F. Intake swirl-a major disturbance parameter in engine/intake compatibility[C]∥Proceedings of the 13th Congress of ICAS/AIAA. Bonn: ICAS, 1982: 1415-1424.

[6] SCHMID N R, LEINHOS D C, FOTTNER L. Steady performance measurements of a turbofan engine with inlet distortions containing co- and counter-rotating swirl from an intake diffuser for hypersonic flight: 2000-GT-0011[R]. New York: ASME, 2000.

[7] STOCKS C P, BISSINGER N C. Design and development of tornado engine air intake: AGARD CP-301[R]. Brussels: AGARD, 1981.

[8] SAE International. A methodology for assessing inlet swirl distortion: AR 5686[S]. Warrendale, PA: SAE International, 2010.

[9] SHEORAN Y, BOULDIN B, KRISHNAN P M. Compressor performance and operability in swirl distortion[J]. Journal of Turbomachinery, 2012, 134(4): 041008.

[10] 屠宝锋， 胡骏， 张凯. 对涡旋流影响压气机转子性能和稳定性的研究[J]. 推进技术， 2016, 37(4): 640-645.

TU B F, HU J, ZHANG K. Effects of twin swirl on performance and stability of compressor rotor[J]. Journal of Propulsion Technology, 2016, 37(4): 640-645(in Chinese).

[11] 张晓飞， 姜健， 符小刚. S弯进气道旋流畸变数值模拟及特性分析[J]. 燃气涡轮试验与研究, 2012, 25(3): 21-26.

ZHANG X F, JIANG J, FU X G. Numerical simulation and characteristic analysis of swirl distortion in S-duct inlet[J]. Gas Turbine Experiment and Research, 2012, 25(3): 21-26 (in Chinese).

[12] XIE W Z, GUO R W. A ventral diverterless high offset S-shaped inlet at transonic speeds[J]. Chinese Journal of Aeronautics, 2008, 21(3): 207-214.

[13] 叶飞， 张堃元， 姜健， 等. 进气道旋流模拟及测量的实验研究[J]. 推进技术, 2009, 30(3): 297-301.

YE F, ZHANG K Y, JIANG J, et al. Experimental investigation on simulation and measurement for intake swirl[J]. Journal of Propulsion Technology, 2009, 30(3): 297-301 (in Chinese).

[14] 刘雷， 陈浮， 宋彦萍， 等. 大量附面层吸入S弯进气道内吹气控制[J]. 航空动力学报， 2015, 30(10): 2498-2507.

LIU L, CHEN F, SONG Y P, et al. Blowing control in S-shaped inlet with significant boundary layer ingestion[J]. Journal of Aerospace Power, 2015, 30(10): 2498-2507 (in Chinese).

[15] 李大伟， 马东立. 背负式S形进气道流场控制技术[J]. 北京航空航天大学学报, 2008, 34(12): 1456-1459.

LI D W, MA D L. Improving dorsal S-shaped inlet performance by vortex flow control[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(12):1456-1459 (in Chinese).

[16] DA X, FAN Z, FAN J, et al. Microjet flow control in an ultra-compact serpentine inlet[J]. Chinese Journal of Aeronautics， 2015, 28(5): 1381-1390.

[17] LAWLEY T, PRICE D. A miniature three-dimensional pressure probe[J]. Review of Scientific Instruments, 1971, 42(1): 158-160.

[18] ALLIANTECH. Multi-hole velocity probes[R]. Gennevilliers: Aeroprobe Corporation, 2010.

[19] JOHANSEN E S, REDINIOTIS O K, JONES G. The compressible calibration of miniature multi-hole probes[J]. Journal of Fluids Engineering, 2001,123(1): 99-111.

[20] RAMAKRISHNAN V, REDINIOTIS O K. Calibration and data-reduction algorithms for nonconventional multihole pressure probes[J]. AIAA Journal, 2005, 43(5): 941-952.

[21] 刘大响. 航空燃气涡轮发动机稳定性设计与评定技术[M]. 北京： 航空工业出版社, 2004: 33-41.

LIU D X. Stability design and evaluation technique of aero gas turbine engine[M]. Beijing: Aviation Industry Press, 2004: 33-41 (in Chinese).

[22] 彭成一， 马家驹， 尹军飞. 新机试飞中的进气道旋流测量[J]. 推进技术, 1994, 15(4): 8-13.

PENG C Y, MA J J, YIN J F. Measurement of inlet swirls in flight[J]. Journal of Propulsion Technology, 1994, 15(4): 8-13 (in Chinese).

[23] TOURNIER S E. Flow analysis and control in a subsonic inlet[D]. Boston, MA: Massachusetts Institute of Technology, 2005.

five-holeprobe

XUZhulin,DAXingya*,FANZhaolin

HighSpeedAerodynamicsInsititute,ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China

ThedorsalS-shapedinletpossessesanexcellentabilityofforwardradarstealthandbenefitsthedisposaloflandinggearsandthemissile,butthenon-uniformflowfieldintheoutletinfluencesthestabilityoftheengineseriously.Besidestotalpressuredistortionandtotaltemperaturedistortion,swirldistortionisalsooneimportantembodimentofnon-uniformity.Toresearchthecharacteristicsofswirldistortion,thispaperusestheassessmentmethodologyofSocietyofAutomotiveEngineers(SAE)andarotationalfive-hole-probe-basedmeasurementtoassessthehighlyswirlingflowfieldofthedorsalserpentineinletatMachnumbersbetween0.2and0.6.TheresultsindicatethatthechangeoftheSwirlDirectivity(SD)andSwirlPairs(SP)isnotapparentduringtheappointedmachrange,andthereisapairedswirlinweaksymmetryintheoutlet.Themaximumswirlangleismorethan40°.SwirlIntensity(SI)increasesfrom6°intheinternalringto13°intheexternalring,withoutapparentchangeatMachnumbersbelow0.5.AlthoughtheassessmentofSAEhasidentifiedthemodeofswirl,itsswirlintensitydescriptordoesnotmanifestthestateofhighswirling,impedingtheapplicationofSAE’sassessmentmethodologytoassessmentofconsistencybetweeninletsandengines.

S-shapedinlet;five-holeprobe;vortex;separatedflow;swirldistortion

2017-04-21；

2017-05-16；

2017-06-27；Publishedonline2017-07-071148

URL：http://hkxb.buaa.edu.cn/CN/html/20171205.html

NationalNaturalScienceFoundationofChina(11602291)

.E-maildxingya@163.com

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.121342

2017-04-21；退修日期2017-05-16；录用日期2017-06-27；网络出版时间2017-07-071148

http://hkxb.buaa.edu.cn/CN/html/20171205.html

国家自然科学基金(11602291)

.E-maildxingya@163.com

徐诸霖，达兴亚，范召林．基于五孔探针的大S弯进气道旋流畸变评估J． 航空学报,2017,38(12):121342.XUZL,DAXY,FANZL.Assessmentofswirldistortionofserpentineinletbasedonfive-holeprobeJ.ActaAeronauticaetAstronauticaSinica,2017,38(12):121342.

V211

A

1000-6893(2017)12-121342-10

王娇)

Assessmentofswirldistortionofserpentineinletbasedon