七阶正交容积卡尔曼滤波算法

孟东，缪玲娟，邵海俊，沈军

北京理工大学 自动化学院，北京 100081

七阶正交容积卡尔曼滤波算法

孟东，缪玲娟*，邵海俊，沈军

北京理工大学 自动化学院，北京 100081

在高斯滤波框架下，阶次越高，近似精度越高。为提高滤波精度，通过提高阶次，提出了七阶正交容积卡尔曼滤波(CQKF)算法。在传统CQKF算法的基础上，该算法扩展了线性积分的近似阶次，提出了七阶球面积分的确定性采样方法；进而扩展了球-半径准则，提高了滤波估计精度。飞行器目标跟踪的仿真实验证明了该算法的有效性，证明了七阶CQKF比五阶CQKF、三阶容积卡尔曼滤波器(CKF)和无迹卡尔曼滤波器(UKF)有更高的滤波精度。

高阶正交滤波器；CKF；飞行器目标跟踪；七阶CQKF；UKF

卡尔曼滤波(KF)算法已经广泛用于动态系统的滤波估计应用中[1]。例如，卡尔曼滤波算法应用在捷联惯导系统中的初始对准过程中，能有效减小非线性模型误差，减小失准角，提高系统初始对准的精度[2]；KF应用在组合导航系统(INS/GPS)中，降低了导航信号的系统噪声和观测噪声，提高了导航精度[3]；KF应用在雷达跟踪系统中，解决了七维状态的雷达跟踪难题，提高了跟踪精度[4]。在此基础上，发展出多种相关算法，有卡尔曼滤波(EKF)、无迹卡尔曼滤波(UKF)、容积卡尔曼滤波(CKF) 、正交容积卡尔曼滤波(CQKF) 、内嵌容积卡尔曼滤波(ICKF)等算法。EKF算法完成了对滤波对象的一阶线性化，实现了KF滤波的初级应用[5-6]。UKF算法引入了确定性采样的策略，处理了高非线性动态系统的估计问题[7-9]，能达到三阶的测量精度。CKF算法采用了比UKF更好的采样策略，增强了滤波的稳定性[10-11]。CQKF算法用采样点近似的方法实现了对线积分的近似，提高了球-半径准则中线积分的近似精度，进一步增强了滤波的精度[12-13]。近年来，高阶滤波精度的算法不断被提出来。五阶UKF[14]、五阶CKF[15]、五阶嵌入式卡尔曼滤波(ECKF)算法[16]、五阶ICKF[17]、高阶CQKF[13]等高阶算法的提出，都提高了原三阶算法的滤波精度。高阶算法能增加确定性采样的采样点个数，并在高斯近似理论中，取得高于低阶算法的近似精度。但是，由于高阶算法的复杂度较高，高阶算法的采样点的点集较难确定，因此，高于五阶精度的高阶算法较少被提及。

为进一步提高滤波精度，本文提出了七阶正交容积卡尔曼滤波(7th-CQKF)算法。在传统的高阶CKF算法基础上，本文扩展了球-半径采样准则，确定了7th-CQKF的采样方法；在高斯滤波器的框架下，详细推导出新滤波算法步骤。仿真结果证明，新方法提升了滤波精度。

1 三阶容积卡尔曼滤波(3rd-CKF)

传统的CKF滤波器建立在非线性离散动态系统上，令离散控制系统状态方程和量测方程的非线性模型为

xk=f(xk-1,uk-1)+wk-1

(1)

zk=h(xk,uk)+vk-1

(2)

式中:xk为k时刻的状态量；f和h为非线性函数；zk为测量值；uk为控制输入；wk-1和vk-1是零均值、协方差分别为Qk-1和Rk-1的加性高斯白噪声。对任意阶函数f(x)，其积分可表示为[10]

If=

(3)

可被分解为两类积分，分别为线积分和球面积分，则有

If=

(4)

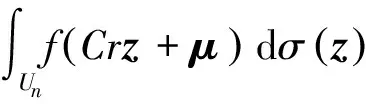
(5)

三阶CKF化简为由一组2n个等权值的容积点(采样点)来实现积分的数值逼近，共有2n个采样点。这就是CKF算法的基本思想。

2 七阶正交容积卡尔曼滤波(7th-CQKF)

CQKF算法[12]在CKF算法的基础之上，对线积分使用切比雪夫-拉盖尔多项式得到正交点，实现对线积分的采样，并降低了容积准则的扩展难度。文献[13]中的高阶CQKF算法扩展了正交容积准则，将近似精度提高到五阶。本文推导了七阶正交容积准则，首次确定了在正交容积准则的前提下，七阶准则下CQKF的采样点及其权重，得到7th-CQKF算法。

首先，任意阶次函数的积分形式式(4)包含两类积分，第1种是线积分形式，即

(6)

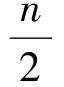
(7)

文献[15]已经证明，如果积分式(4)中要达到七阶精度，那么，必须满足两类积分同时达到七阶精度。同理，本文推导线积分和球面积分的采样准则，使两类积分准则均达到七阶近似精度，以获得七阶精度的CKF滤波算法。

2.1 七阶线积分准则

对于式(6)，根据文献[12-13]，应用高斯-拉盖尔正交准则(GGLQ)，线积分可用正交点近似为

(8)

式中：n′为近似阶次，正交点λi′可由m阶的切比雪夫-拉盖尔等式确定[18-19],即

(9)

采样点计算公式为

(10)

式中：α=n/2-1，当维数n确定后，解方程后可以得到n′个λ值，即n′个正交采样点λi′。其相应的权重为

(11)

解以上方程，可得到3维下的线积分采样点λi′；同理，在不同n下的方程，计算线积分采样点，如表1所示。

表1 七阶线积分采样点Table 1 Seventh-degree sampling points of line integral

解不同维数n下的七次方程，易得到任意维下的线积分采样点，采样点的个数等于n′。当n′=7时，式(8)即为本文所扩展的七阶线积分准则。

2.2 七阶球面积分准则

文献[16]在文献[17]基础之上，提出了基于拉格朗日插值定理的球面积分准则，该准则结论如下：

定理1球面积分U(f)能达到2m+1阶精度，可表示为

(12)

式中：ωp和G(up)分别定义为

(13)

(14)

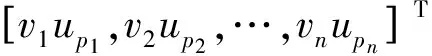
Γ((kn+1)/2)

(15)

为得到七阶球面积分准则，按照降序分类-非降序排列-对称采点等3大步骤，完成了七阶算法的采点。

首先，用降序排列法对p的组合方式分类。分析式(13)和式(14)：

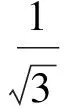
ωh1=ω(3,0,0,…,0)=

(16)

(17)

(18)

式中：An为n维球体的表面积。

其次，在p不按降序排列的条件下，分别讨论p的不同组合的情况。

1) 与组合p=[3,0,0,0,…,0]等权重的方式有[0,3,0,0,…,0][0,0,3,0,…,0][0,0,0,…,3]，共有n个组合。

2) 与组合p=[2,1,0,0,…,0]等权重的方式有[2,0,1,0,…,0][2,0,0,1,0,…,0][2,0,0,0,…,1]，[0,2,1,0,0,…,0][0,2,0,1,0,…,0][0,2,0,0,1,0,…,0][0,2,0,0,0,…,1]…[0,…,0,0,2,0,1][0,…,0,0,0,2,1]，及数字2和1交换位置后的组合[1,0,2,0,…,0][1,0,0,2,0,…,0][0,0,…,0,1,2]，共有n(n-1)个组合。

3) 与组合p=[1,1,1,0,0,…,0]等权重的方

式有[1,1,0,1,…,0][1,1,0,0,1,…,0]…[1,1,0,0,0,…,1]，[1,0,1,1,0,…,0][1,0,1,0,1,0,…,0]…[1,0,1,0,…,0,1]…[0,0,0,0,…,1,1,1]，共有n(n-1)(n-2)/6个组合。

以上分析的每一种组合，各组均有各自相同的权重，如：

ωh1=ω(3,0,0,…,0)=ω(0,3,0,L,0)=…=

ω(0,0,0,…,3)

ωh2=ω(2,1,0,…,0)=ω(2,0,1,…,0)=…=

ω(0,…,0,1,2)

ωh3=ω(1,1,1,0,…,0)=ω(1,1,0,1,…,0)=…=

ω(0,…,0,1,1,1)

对于这3类组合，其每一类组合的总权重为

七阶球面准则有3种算子的组合方式，如式(12)所示，3种算子组合及其相应权重，构成了对积分的七阶近似。每种算子组合对应于一种采样方式。当为第1种组合时，定义为h1采样，其中一个算子为p=[3,0,0,…,0]，共有n个组合方式，每一次h1采样的采样点个数为2n；当为第2种组合时，定义为h2采样，其中一个算子为p=[2,1,0,…,0]，共有n(n-1)个组合方式，每一次h2采样的采样点个数为4n(n-1)；当为第3种组合时，定义为h3采样，其中一个算子为p=[1,1,1,0,…,0]，共有n(n-1)(n-2)/6个组合方式，每一次h3采样的采样点个数为4n(n-1)(n-2)/3。根据以上分析，每一类采样点的权重为

(19)

最后，结合式(12)，根据以上分析和采样点集的对称性，当m=3时，七阶球面积分的表达式为

f(m6j)+f(-m6j)+f(m7j)+f(-m7j)+f(m8j)+f(-m8j)]

(20)

式中的3种采样方式分别是h1、h2和h3采样。具体总结为

1)h1采样h1：包括点集ej和-ej，与式(6)定义相同，ej为单位矩阵的第j列向量，共有2n个采样点。

2)h2采样h2：包括点集{m1}{m2}{m3}{m4}，分别定义为

(21)

式中：ek和eg分别为单位矩阵的第k和g列向量，每一次h2采样共有4n(n-1)个采样点。

3)h3采样h3：包括点集 {m5}{m6}{m7}和{m8} ,分别定义为

(22)

式中：每一次h3采样共有4n(n-1)(n-2)/3 个采样点；ek、eg和et分别为单位矩阵的第k、g和t列向量。则式(20)简化表达为

(23)

式中：G(up)代表积分近似过程中的采样部分；f(h1)代表对函数f的一次h1采样；f(h2)代表对函数f的一次h2采样；f(h3)代表对函数f的一次h3采样。

式(20)完成了七阶球面积分的分解，共有采样点2n+4n(n-1)+4n(n-1)(n-2)/3=2n(2n2+1)/3个。式(20)～式(23)就是本文推导出的七阶球面积分准则。

2.3 七阶正交球-半径准则

If=

(24)

根据式(12)～式(14)，将式(24)代入球面积分准则得

If=

(25)

根据式(20)～式(23)，线积分采样个数n′=7，式(25)中代入线积分采样准则，七阶正交容积球-半径准则可以表示为

If=

(26)

由式(11)和式(19)可知，球面积采样个数Ns=2n(2n2+1)/3，式(26)各系数及半径均已知。令式(26)的各采样部分的权重系数分别为A、B和C，If简化为

(27)

式中：h1、h2和h3代表球面积分准则的3种采样方式。参考式(20)和式(27)中子项表示为

(28)

(29)

(30)

(31)

(32)

(33)

式(27)就是本文推导出的七阶容积卡尔曼滤波公式。令式(27)的简化模型为

(34)

则其相应的容积点和权值为

εi=

(35)

ωi=

(36)

式中：i′=1,2,…,7；h1i代表该采样方法的第i个采样点；滤波维数n确定后，每种采样方式的采样点个数是固定的。

式(27)～式(36)就是本文提出的7th-CQKF算法的基本公式。7th-CQKF算法的采样点总数为14n(2n2+1)/3。7th-CQKF算法提高了滤波算法的近似精度，比5th-CQKF、3rd-CKF算法的滤波精度高。

7th-CQKF算法的步骤：

1) 初始化

(37)

式中：E为期望值；Chol为乔列斯基(Cholesky)分解；S0为方差p0的均方根。

2) 计算正交点

计算线积分采样点λi′，并求出七阶正交容积权重Ai′,Bi′,Ci′。如2.1节表1所示。式(38)～式(44)为时间更新方程。

3) 假定在时刻k-1

(38)

(39)

4) 估计容积点

(40)

5) 估计传播容积点

(41)

6) 估计预测状态和协方差

令v=14n(2n2+1)/3，

(42)

(43)

(44)

式中：Qk-1是过程噪声方差。式(45)～式(52)为测量更新方程。

7) 估计容积点

(45)

8) 估计传播容积点

zi,kk-1=h(xi,kk-1,uk)

(46)

9) 估计预测测量值

(47)

10) 估计方差和协方差矩阵

(48)

zi,k-1k-1)T

(49)

11) 估计卡尔曼滤波增益

(50)

12) 估计更新状态

(51)

13) 估计相应的方差

(52)

14)跳转到步骤2)，更新均值与方差后，继续下一次7th-CQKF滤波算法，直到滤波循环结束。

2.4 高阶算法的对比

分析三阶、五阶、七阶卡尔曼滤波算法的特点。

首先，本文提出的7th-CQKF滤波算法与传统的CKF、5th-CKF的采点方法不同。

7th-CQKF滤波算法在求解半径积分准则的过程中，采用了高斯-拉格朗日正交准则[16]；传统的CKF、5th-CKF则采用了线积分准则[10]。高斯-拉格朗日正交准则比线积分准则有更高的近似精度。同时，高斯-拉格朗日正交准则的扩展性好，可以近似任意精度的半径积分，具有较低的复杂度。而传统的CKF、5th-CKF则采用了线积分准则，扩展性不好，在高阶扩展过程中，有自由变量的产生，算法不唯一。以下举例分析其不唯一性。

文献[15]提出的5th-CKF滤波算法理论，在求解半径准则时，需求解方程：

(53)

式(53)中有一个自由变量，该方程必须在自由变量确定后，才能求解，自由变量的确定具有不唯一性，此特性增加了5th-CKF的推导难度和复杂度，使5th-CKF的形式不唯一。更进一步，当CKF算法推广到七阶精度时，7th-CKF具有两个自由变量，算法不唯一，进一步增加了算法的复杂度。

根据本文推导的式(8)～式(11)可发现，7th-CQKF算法的形式唯一，不存在自由变量，推导过程简洁，算法的复杂度较低。因此，本文提出的7th-CQKF滤波算法，改进了半径准则的求解方法，降低了原高阶CKF算法的复杂度。

其次，各方法采样方法不同，其采样点个数也不相同。采样点个数与算法的计算量成正比例关系。统计每个算法在一次滤波中的采样点个数，如表2所示。

分析表2可知，滤波阶次的提高会增加算法的采样点个数。在考虑计算量的前提下，应该根据实际应用环境，按照可容忍的计算量的大小，选择合适的滤波算法，以在计算量和精度之间达到平衡。因此，高阶算法在实际应用中，需使用高性能的硬件系统处理数据，以提高高阶算法的实时性。

7th-CQKF的采样点数量反映了算法计算量的大小，且与系统状态的维数n相关。当n≤5时，7th-CQKF算法的计算量与CKF、5th-CKF、5th-CQKF的计算量有一定的差异，但基本都在可容忍的计算量范围之内；当n>5时，7th-CQKF算法的计算量与CKF、5th-CKF、5th-CQKF开始有明显的差别，因计算量的增加而对原系统的影响开始显著，此时，需使用高性能的信号处理系统，以减弱计算量带来的影响，例如，使用高性能的FPGA、DSP等处理器，均具有较好的效果。

最后，在理论上，算法的阶次越高，滤波精度越高。阶次代表了在积分近似过程中，泰勒级数的余项能够近似的最高幂的次数。因此，7th-CQKF滤波算法在理论上的滤波精度高于CKF、5th-CKF、5th-CQKF算法。

表2 采样点个数对比Table 2 Comparison of number of sampling points

总之，利用改进的球-半径准则方法，7th-CQKF算法能够取得高于CKF、5th-CKF、5th-CQKF算法的滤波精度。

3 仿真结果及分析

本文通过仿真实验，检验多个滤波算法对非线性系统的滤波能力，对比各算法在高斯环境下的滤波精度，以验证7th-CQKF的优良滤波性能。这些算法分别为：UKF算法、CKF算法、5th-CQKF算法、7th-CQKF算法。

本文验证高维状态向量下的非线性模型系统为[13,22-24]：

xk=

wk-1

(54)

(55)

(56)

其中：x0=[1000 300 1000 0 -3×10-3]T为状态向量的初值，时间间隔T=1 s，协方差矩阵P0=diag(100 10 100 10 100)T。在每一次的运行中，初值状态在分布N(x0,P0)下随机选取，4种算法在相同的初始条件下运行，仿真时间100 s，运行50次的蒙特卡罗试验。截取10 s至100 s的仿真结果，通过对比4种算法在这种仿真环境下状态估计误差的均方误差(RMSE)，判断滤波性能的好坏。RMSE定义为

(57)

图1 跟踪轨迹图
Fig.1 Track diagram

图2 第1个状态向量的均方误差
Fig.2 RMSE of the first state variable

分析图2～图6可知，5个状态向量的RMSE均是7th-CQKF算法最小，且7th-CQKF算法比5th-CQKF算法、CKF算法、UKF算法的滤波精度高；由RMSE的波动范围可知，UKF算法的波动最大， 7th-CQKF算法、5th-CQKF算法、CKF算法比UKF算法的稳定性高。证明了本文提出的7th-CQKF算法，在提出的新采样方法下，提高了滤波算法的精度。

图3 第2个状态向量的均方误差
Fig.3 RMSE of the second state variable

图4 第3个状态向量的均方误差
Fig.4 RMSE of the third state variable

图5 第4个状态向量的均方误差
Fig.5 RMSE of the fourth state variable

图6 第5个状态向量的均方误差
Fig.6 RMSE of the fifth state variable

4 结 论

本文通过提高球-半径准则的近似阶次，进行理论推导，提出了7th-CQKF算法，提高了滤波精度，得出以下结论：

1) 扩展了球-半径准则，在五阶球-半径准则基础上，分别提出了七阶线积分准则和七阶球面积分准则，进而提出七阶正交球-半径准则；在七阶近似下，确定了七阶正交球-半径准则的3种确定性采样方法及其权重函数。

2) 在高斯滤波基础上，根据提出的七阶正交球-半径准则，提出7th-CQKF算法，详细推导了7th-CQKF算法的滤波步骤。

3) 通过仿真对比，证明7th-CQKF算法比传统的UKF算法、CKF算法、5th-CQKF算法的滤波精度高；7th-CQKF算法、5th-CQKF算法、CKF算法均比UKF算法的稳定性高。

[1] KALMAN R E. A new approach to linear filtering and prediction problems[J].Transaction of the ASME-Journal of Basic Engineering, 1960, 82(Series D): 35-45.

[2] CUI B B, CHEN X Y, TANG X H. Improved cubature Kalman for GNSS/INS based on transformation of posterior sigma-points error[J]. IEEE Transactions on Signal Processing, 2017, 65(11): 2975-2987.

[3] HU G G, GAO S S, ZHONG Y G. A derivative UKF for tightly coupled INS/GPS integrated navigation[J]. ISA Transactions, 2015, 56: 135-144.

[4] KULIKOV G Y, KULIKOVA M V. Accurate continuous-discrete unscented Kalman filtering for estimation of nonlinear continuous-time stochastic models in radar tracking[J]. Signal Processing, 2017, 139: 25-35.

[5] BUCY R S, SENNE K D. Digital synthesis of non-linear filters[J]. Automatica, 1971, 7(3): 287-298.

[6] SUNAHARA Y, YAMASHITA K. An approximate method of state estimation for non-linear dynamical systems with state-dependent noise[J]. Journal of Fluids Engineering, 2009, 92(2): 385.

[7] JULIER S J, UHLMANN J K. A new extension of the Kalman filter to nonlinear systems[J]. Proceedings of the Society of Photo-optical Instrumentation Engineers, 1997,3068(1): 182-193.

[8] JULIER S J, UHLMANN J K. Unscented filtering and nonlinear estimation[J].Proceedings of IEEE, 2004,92(3): 401-422.

[9] ITO K, XIONG K. Gaussian filters for nonlinear filtering problems[J]. IEEE Transactions on Automatic Control,2000, 45(5): 910-927.

[10] ARASARATNAM I, HAYKIN S. Cubature Kalman filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269.

[11] ARASARATNAM I, HAYKIN S, HURD T R. Cubature Kalman filtering for continuous-discrete systems: Theory and simulations[J]. IEEE Transactions on Signal Processing, 2010, 58(10): 4977-4993.

[12] BHAUMIK S, SWATI. Cubature quadrature Kalman filter[J]. IET Signal Processing, 2013, 7(7): 533-541.

[13] JIA B, XIN M, CHENG Y. Higher degree cubature quadrature Kalman filter[J]. Automatica, 2013, 49(1): 510-518.

[14] WU Y, HU D, WU M. A numerical-integration perspective on Gaussian filters[J].IEEE Transactions on Signal Processing, 2006, 54(8): 2910-2921.

[15] JIA B, XIN M, CHENG Y. High-degree cubature Kalman filter[J]. Automatica, 2013, 49(2): 510-518.

[16] GENZ A. Fully symmetric interpolatory rules for multiple integrals over hyper-spherical surfaces[J]. Journal of Computational and Applied Mathematics, 2003, 157(1): 187-195.

[17] SILVESTER P. Symmetric quadrature formulae for simplexes[J]. Mathematics of Computation, 1970, 24(109): 95-100.

[18] ZHANG Y G, HUANG Y L, LI N, et al. Embedded cubature Kalman filter with adaptive setting of free parameter[J]. Signal Processing, 2015, 114(C): 112-116.

[19] ZHANG Y G, HUANG Y L, LI N, et al. Interpoltory cubature Kalman filter[J]. IET Control Theory Applications, 2015(9): 1731-1739.

[20] KRYLOV V I. Approximate calculation of integrals[M]. New York: Dover Publication, 2005: 58-66.

[21] HILDEBRAND F B. Introduction to numerical analysis[M]. 2nd ed. New York: Dover Publication, 2008: 195-198.

[22] WU H, CHEN S X. Robust range-parameterized cubature Kalman filter for bearings-only tracking[J]. Journal of Central South University, 2016, 23(6): 1399-1405.

[23] WU H, CHEN S X. Ranre-parameterized orthogonal simplex cubature Kalman filter for bearings-only measurements[J]. IET Science, Measurement Technology, 2016, 10(4): 370-374.

[24] XU B, ZHANG P, WEN H Z. Stochastic stability and performance analysis of cubature Kalman filter[J]. Neurocomputing, 2016, 186(C): 218-227.

Aseventh-degreecubaturequadratureKalmanfilter

MENGDong,MIAOLingjuan*,SHAOHaijun,SHENJun

CollegeofAutomation,BeijingInstituteofTechnology,Beijing100081,China

IntheGaussianfilterframe,thehighertheorder,thehighertheaccuracyoftheapproximation.Toimprovethefilteringaccuracy,aseventh-degreeCubatureQuadratureKalmanFilter(CQKF)algorithmisproposedbyimprovingthedegree.BasedonthetraditionalCQKF,thealgorithmextendstheapproximatedegreeoflinearintegrals,andproposesadeterministicsamplingmethodfortheseven-degreesphericalintegral.Thenthespherical-radialruleisextendedtoimprovetheaccuracyofthefilter.Thesimulationresultsoftheaircrafttargettrackingdemonstratetheeffectivenessofthealgorithm.Itisprovedthattheseventh-degreeCQKFismoreaccuratethanthefifth-CQKF,third-degreeCubatureKalmanFilter(CKF)andUnscentedKalmanFilter(UKF).

high-degreeorthogonalfilter;CKF;aircrafttargettracking;seventh-degreeCQKF;UKF

2017-05-12；

2017-05-24；

2017-08-15；Publishedonline2017-08-201717

URL：http://hkxb.buaa.edu.cn/CN/html/20171227.html

s：NationalNaturalScienceFoundationofChina(61153002,61473039)

.E-mailmiaolingjuan@bit.edu.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.321410

2017-05-12；退修日期2017-05-24；录用日期2017-08-15；网络出版时间2017-08-201717

http://hkxb.buaa.edu.cn/CN/html/20171227.html

国家自然科学基金(61153002,61473039)

.E-mailmiaolingjuan@bit.edu.cn

孟东，缪玲娟，邵海俊，等．七阶正交容积卡尔曼滤波算法J． 航空学报,2017,38(12):321410.MENGD,MIAOLJ,SHAOHJ,etal.Aseventh-degreecubaturequadratureKalmanfilterJ.ActaAeronauticaetAstronauticaSinica,2017,38(12):321410.

V419+.9

A

1000-6893(2017)12-321410-11

苏磊，蔡斐)