基于能量理论的航空整体结构件滚压变形校正载荷预测方法

路来骁，孙杰,，韩雄，熊青春，宋戈

1.山东大学 机械工程学院 高效洁净机械制造教育部重点实验室，济南 250061 2. 中航工业成都飞机工业(集团)有限责任公司，成都 610092

基于能量理论的航空整体结构件滚压变形校正载荷预测方法

路来骁1，孙杰1,*，韩雄2，熊青春2，宋戈2

1.山东大学 机械工程学院 高效洁净机械制造教育部重点实验室，济南 250061 2. 中航工业成都飞机工业(集团)有限责任公司，成都 610092

航空整体结构件在数控加工过程中，由于多种因素耦合作用影响，普遍存在不同程度、不同形式的加工变形问题。滚压校正是实现大长宽比薄壁结构件变形校正的有效手段，且在获得工件尺寸精度的同时，引入压应力，提高工件使用寿命。目前，滚压变形校正多依赖于工人经验和试错法，缺乏校正载荷的准确预测方法，质量稳定性差。为此，基于能量理论，在分析梁类零件校正过程能量平衡要求的基础上，结合等效截面法和弯曲应变能法，分别对变形工件的弯曲应变能和滚压做功进行计算，进而建立工件变形量与校正载荷间的数学模型，实现滚压变形校正载荷预测。进一步，为实现校正载荷准确性的快速评价，采用直接应力法建立了加工变形-滚压校正协同仿真环境，实现了梁类航空整体结构件滚压变形校正的快速等效模拟。最后，以三隔框结构件为例进行了有限元仿真和试验验证，直接应力法仿真分析获得的变形消除率为94.5%，试验获得的单次滚压变形消除率达到82.0%，滚压区域表面由铣削拉应力转变为滚压压应力，校正效果符合预期。

航空整体结构件；滚压；变形校正；载荷预测；有限元方法

随着现代飞机对高速、高机动性、高负载和服役寿命要求的不断提高，航空整体结构件因重量轻、结构效率高、可靠性好等优点在飞机结构设计中获得大量应用[1]。航空整体结构件是构成飞机机体骨架和气动外形的重要组成部分，大多为具有复杂型腔、筋条的大型薄壁结构，采用毛坯直接铣削加工而成，其材料去除率高、几何结构不对称、自身刚度低，极易产生加工变形[2]。

国内外学者围绕整体结构件加工变形机理及影响因素开展了大量研究，发现毛坯残余应力是影响铝合金整体结构件加工精度的关键因素[3-4]。同时，加工过程中切削力和切削热引入了加工应力，而加工应力对薄壁工件的形状精度同样具有重要影响[5-7]。张铮[8]将初始残余应力视为材料制备工艺残留能量，加工残余应力视为引入的外部能量，采用能量理论分析加工变形问题。黄晓明等[9]采用了等效刚度法，实现了复杂整体结构件加工变形预测。相关学者进而提出了加工变形控制方法，例如：Chantzis等[10]通过优化零件位于板材的位置降低初始残余应力的影响，Li等[11]通过控制切削参数降低加工应力的影响。但是，航空整体结构件加工变形现象依然非常严重。据波音公司统计，因工件变形问题造成的损失每年高达2.9亿美元[10]。根据对国内航空企业的调研，约有55%的工件存在加工变形问题，并且有50%的变形工件需采取进一步的工艺措施以确保最终尺寸精度[12]。

变形校正是保证航空整体结构件加工精度、满足飞机装配要求的重要保障。针对铝合金航空整体结构件，常用校正手段主要包括压力校正、喷丸校正、滚压校正等。压力校正适用于多数梁类整体结构件，孙杰[13]针对梁类结构件的主要截面特征为U型截面这一特点，建立了简化的U型截面工件弯曲变形校正数学模型；张洪伟等[14-15]建立了加工变形-校正协同仿真环境，利用改进的二分法进行校正参数计算。但是，压力校正会引入较大幅值的残余拉应力，对工件的疲劳寿命产生不利影响，喷丸校正和滚压校正可有效避免这一问题。喷丸和滚压作为表面处理技术，可在工件表层及浅表层引入塑性变形和残余压应力，具有提高材料表面质量完整性、改善微观组织结构、强化疲劳性能的优点[16-17]。喷丸校正分为普通喷丸、超声喷丸和激光喷丸，适用于薄板、壁板、叶片和焊接区域的变形校正[18]。滚压变形校正基本原理为对变形区域凹侧的薄壁顶部施加滚压操作，使顶部材料塑性变形伸长发生反向变形，进而与加工变形相抵消。滚压校正充分利用了薄壁结构的特点，适用于梁类、壁板类等大多数铝合金航空整体结构件。

滚压变形校正作为新兴的校正手段，具有安全性高、操作方便等优势。但是，滚压校正操作严重依赖于工人经验，通过试错法不断调整校正载荷，往往一个零件的校正需要重复多次滚压，不但耗费大量时间，而且校正质量难以保证，质量稳定性差。因此，航空整体结构件滚压变形校正的主要问题就是校正载荷的准确预测。王中秋[19]建立了滚压仿真模型，基于大量仿真结果建立了滚压变形校正图谱。课题组在前期以典型T型件为研究对象，获得了滚压参数和工件变形之间的关系，建立了校正载荷计算方法[20-21]。

目前关于航空整体结构件变形校正的研究多基于简单截面零件，或对复杂零件建立有限元模型一事一议，缺乏成熟的变形校正理论支撑，且其截面惯性矩等截面参数计算困难，缺乏校正载荷准确性的快速评价方法。本文基于能量理论及等效截面惯性矩法，对校正过程所满足的能量平衡方程进行分析，将滚压校正过程视为弯曲应变能与滚压做功的平衡过程，进而实现附加滚压校正力矩的有效预测。通过等效代替法，实现了梁类整体结构件滚压变形校正仿真分析，结合试验验证了基于能量法的校正载荷预测方法的准确性。

1 校正载荷求解

1.1 滚压变形校正基本原理

针对梁类整体结构件滚压变形校正，从能量角度进行分析。工件加工完成后，在板材初始应力、加工应力等因素作用下，发生弯曲变形，这种变形可以表示为初始应力、切削应力等因素引起的外部力矩对工件整体做功，变形工件蕴含着弹性势能，即弯曲应变能。通过对工件特定部位的滚压操作，引入滚压应力，并将其等效为校正力矩，使工件产生反方向的弯曲变形，最终实现工件变形校正，如图1所示。图中，-σ为滚压应力，H为应力施加区域的中心线与中性层的距离，MRolling为校正力矩。

实现变形校正的关键是使滚压做功等于弯曲应变能，即：

WRolling=U

(1)

式中：WRolling为滚压做功;U为弯曲应变能。

在滚压过程中，校正力矩由压入量、滚压位置、壁厚等参数决定。通过对梁类整体结构件滚压过程的能量分析，获得准确的滚压参数，即压入量，是实现变形校正载荷预测的有效途径。

图1 滚压变形校正过程
Fig.1 Rolling distortion correction process

1.2 弯曲应变能计算

应变能是指弹性体在外力作用下发生弹性变形而储存在体内的能量，对于梁类整体结构件，由于其结构的复杂性，截面呈现阶跃式变截面特性，不能用传统的工件截面惯性矩方法对其弯曲应变能进行计算。为此，采用等效弯曲应变能法的思想，求取变截面梁的等效截面惯性矩，进而实现变形工件的弯曲应变能计算。

等效弯曲应变能法的基本思想是使整体结构件与具有相同长度的等截面梁等效，利用梁的弯曲变形能来计算复杂变截面梁的等效截面惯性矩。若不考虑扭转的影响，以纯弯曲梁为例，假设作用在梁两端的弯矩为M,则梁弯曲为M/EI的圆弧，截面转角θ可表示为[22]

(2)

式中：l为工件长度；E为弹性模量；I为截面惯性矩。

外载荷M做的功等于梁中储存的弯曲应变能，即

(3)

联立式(2)和式(3)，得到梁的弯曲应变能为

(4)

如果梁不是圆弧纯弯，可以通过微分法计算梁的弯曲应变能。取任意长度为dx的梁单元，其两边的夹角为

(5)

沿着梁的长度进行积分，即可获得长梁的弯曲应变能为

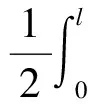
(6)

式中：yx为变形挠度公式。

通过有限元计算变截面梁在外载荷作用下的弯曲变形，提取变形数据并进行多项式拟合，获得变截面梁的变形挠度公式，记为y1。

对于等截面梁，在距端面a处(点C)施加集中载荷P时，其变形形式如图2所示，图中θA、θB分别是等截面梁在支点A、B处转角，b=l-a。则梁的弯曲变形公式y2可根据经典材料力学写出[23]：

(7)

图2 简支梁受集中力弯曲变形
Fig.2Bending deformation for a simply supported beam under a concentrated force

将y1和y2分别代入式(6)进行弯曲应变能计算，令变截面梁和等截面梁的弯曲应变能分别为U1和U2,并令ΔU=U1-U2,则有：

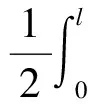
(8)

式中：I*为等效截面惯性矩。

令式(8)中的ΔU=0,则变截面梁的等效截面惯性矩I*可以求出。将I*代入式(4)，则可以获得变截面梁的弯曲应变能为

(9)

对于梁类整体结构件的纯弯曲变形，其变形相对于工件长度均为小变形，其截面转角θ与最大挠度ymax之间的关系为

(10)

将式(10)代入式(9)，得到储存在变截面梁中的弯曲应变能：

(11)

1.3 结构件变形特征分析

图3 典型航空整体结构件滚压校正区域
Fig.3Rolling correction area of a typical monolithic aeronautical component

梁类整体结构件具有复杂的槽腔、加强筋等结构特征，图3所示为一具有n个隔框的长梁结构件，其中第i个隔框的可滚压长度为li,高度为滚轮宽度D。工件加工完成后多发生沿工件长度方向的弯曲变形，采用各段的曲率表征工件的变形情况。

因工件结构和板材初始应力的不连续性，导致工件各段曲率变化。假设工件AB仅在C处结构不连续或应力不连续，则工件的变形挠曲线如图4所示。工件AB变形的挠曲线可分别看成是两段圆弧(ACD和BCE)的组合，每一段都可以通过一个二阶方程表示，在每一段分别有固定的曲率κ1和κ2。因此，根据每个分段的曲率相同，对梁类整体结构件进行分段，将复杂梁类整体结构件简化为相对较小的曲率分段。

因滚轮结构的限制，滚压区域多为不连续的工件侧壁或加强筋，图3中红色框线所示。滚压区域依次定义为R1、R2、…、Rn,其滚压长度分别为l1、l2、…、ln。每个滚压区域包含2～3个可滚压的侧壁或加强筋，因分段的曲率相同，所采用的滚压参数也应相同。

图4 整体结构件加工变形
Fig.4Machining distortion of a typical monolithic aeronautical component

1.4 校正载荷计算

在滚轮的碾压作用下，滚压区域的材料塑性变形伸长，并伴随产生残余压应力，如图1所示。将塑性变形和残余压应力对滚压区域的影响视为校正应力-σ,则引入的校正应力对工件整体产生的校正力矩为MRolling,定义应力施加区域的截面积为S,则校正力矩与校正应力的关系为

MRolling=σSH

(12)

根据圣维南原理和文献[20]研究结论，滚压操作只对实际滚压区域产生影响，即只引起滚压区段内的等截面梁产生弯曲变形。根据能量守恒定律，积蓄在弹性体内的弯曲应变能在数值上等于外力所做的功，滚压做功可以表达为等截面梁在附加弯矩MRolling作用下的弯曲应变能，而等截面梁的弯曲应变能可以通过传统方法进行计算。截面部分的尺寸如图5所示，其截面常数为[13]

Q=wh[α+2β(1-α)]

(13)

(14)

IU-Y=

(15)

式中：α=δ2/h,β=δ1/b,ζ=h1/h,h为截面总高度，w为截面宽度，h1为底面至中性层高度，h2为中性层至顶面高度，δ1为截面侧壁厚度，δ2为底面厚度，Q为截面面积，IU-Y为截面对Y轴的惯性矩。

联立式(2)和式(3)，可以得到弯曲应变能的另一种表达形式,即

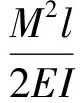
(16)

对于曲率相同的工艺分段，其滚压校正参数相同，即在滚压区域的每个截面引入的校正应力均为-σ,则在该分段内的校正弯矩均为MRolling,所蕴含的弯曲应变能为

(17)

则校正具有n个隔框的长梁所需要的滚压做功为

(18)

联立式(1)、式(11)和式(18)，获得校正该分段工件所需的附加力矩为

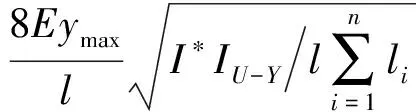
(19)

图5 三隔框整体结构件截面
Fig.5 Cross-section of three-frame integral structure

获得校正该工件所需的附加力矩后，可通过文献[21]给出的公式计算滚压过程的压入量。

2 滚压校正仿真分析

2.1 仿真参数及方法

为实现对滚压校正参数准确性的快速评价，通过有限元软件ABAQUS建立加工变形-滚压校正协同仿真环境。

设计单面三隔框工件，侧壁、加强筋板和腹板厚度均为3 mm，如图6所示。利用式(6)～式(8)并建立相应有限元模型，计算得到其等效截面惯性矩为30 919 mm4。相较于简化的等截面梁的截面惯性矩27 478 mm4提高了12.5%，可见简化法所造成的误差不容忽视。

根据相关研究[3]，在影响航空整体结构件加工变形的众多因素中，板材残余应力是引起铝合金整体结构件加工变形的主要因素，因此忽略加工应力、装夹等其他因素的影响。采用60 mm厚铝合金7050-T7451预拉伸板材为毛坯材料，将初始应力场与毛坯厚度之间的函数关系通过子程序SIGNI施加到毛坯材料模型中。在有限元分析中，材料只发生弹性变形，设置材料弹性模量71.7 GPa和泊松比0.33。采用八节点六面体单元C3D8R对毛坯材料进行网格划分，控制整体网格尺寸为3 mm，对工件侧壁、腹板等区域进行网格细化。采用三点定位原理，对工件底角施加位移约束条件，即限制工件在空间中的位置，又满足工件自由变形的需求。

图6 三隔框整体结构件尺寸
Fig.6 Dimensions of three-frame integral structure

滚压过程为典型的材料非线性过程，直接仿真滚压过程需采用动态显示分析，该方法需耗费大量的时间和计算资源。当整体结构件尺寸较大，而其网格尺寸必然随之增大，降低了仿真分析的准确性。因此，采用与滚压效果等效的加载方式来间接模拟滚压校正过程，是实现大型整体结构件变形校正分析的有效途径，等效载荷的施加方式有面内挤压法、等效热载荷法和直接应力法[24]。直接应力法是指将所需的校正应力作为初始条件施加到变形校正分析模型中，从而获得工件在该校正载荷作用下的变形。经过对简单零件的对比仿真分析，发现直接应力法获得的工件变形规律与实际滚压仿真获得的工件变形规律最接近，误差最小，可以准确地再现工件的滚压变形。

加工变形-滚压校正协同仿真流程及数据传递过程如下：首先，建立毛坯材料模型，利用“生死单元”技术，逐层分区域杀死需要去除的单元，获得工件加工变形数据。同时，提取预设的滚压区域节点编号，分别建立滚压区域集合。其次，利用加工变形仿真结果数据，建立变形校正模型，新模型遗传了加工变形仿真获得的工件变形结果，并通过修改.inp文件，导入滚压区域节点集合，利用载荷施加技术，将计算获得的校正应力施加到滚压区域的节点，实现校正载荷施加。最后，通过静力仿真分析，获得工件最终变形形态。

2.2 结果分析

图7展示了三隔框工件加工变形-滚压校正过程中各分步的应力及变形结果，图中S为应力，S11为沿X方向的应力分量，U为位移，U3为沿Z方向的位移分量。

加工变形仿真分析结束后，工件呈现两端高中间低的弯曲变形，经过滚压变形校正，工件变形状况得到明显改善。选取工件底面腹板中心线为研究路径，提取沿Z方向的节点位移，如图8所示。

从图8可以看出，铣削加工完成后，工件呈现对称的圆弧纯弯，最大加工变形量为0.321 mm。通过式(19)计算获得所需的校正力矩为23 741.965 N·mm，借助式(12)计算得到所需施加的校正应力为29.598 MPa。由于滚压区域为不连续的侧壁段，结合校正后的应力云图显示只在施加载荷的区域存在明显的应力分布，即未滚压的区域仍然保留原始曲率。因此，校正后工件呈现小波浪变形形式，平面度为0.018 mm，工件整体变形量降低了94.4%。通过建立的加工变形-滚压校正协同仿真环境，验证了校正载荷预测的准确性，为工艺制定提供支持。

图7 三隔框整体结构件变形校正仿真分析(×100)
Fig.7Simulation analysis of distortion correction for three-frame integral structure (×100)

图8 仿真变形校正效果评价
Fig.8Simulation effectiveness evaluation of distortion correction

3 三隔框工件滚压校正试验验证

3.1 试验参数

为了验证理论模型和有限元计算的准确性，进行三隔框工件滚压校正试验，如图9所示。

图9 三隔框整体结构件滚压校正试验
Fig.9Test of rolling correction of three-frame integral structure

工件加工完成后，采用双侧壁滚压装置，对工件进行滚压校正操作。采用三坐标测量机Thome Rapid Plus测试滚压前后的变形数据，工件采用三点支撑，以两条侧壁和底角顶点为基准建立工件坐标系，在三隔框工件腹板底面均匀选取5条特征线，每条特征线测量点间距为20 mm，获得工件腹板底面点云数据。为考察滚压校正前后的应力分布，采用Xstress3000应力测试仪对特征点滚压校正前后的表面残余应力进行测试，点P1、P2、 P3位于侧壁，与顶面的距离分别为3、15和27 mm，点P4位于腹板底面中线。其中，点P1位于侧壁的滚压区域。选用Cr靶，衍射角为139.3°，准直器直径为3 mm，为减小滚压前后重复测量造成的误差，每个点测量三次，取平均值。

3.2 结果与讨论

滚压校正前后的工件变形数据如图10所示。铣削加工完成后，工件呈现圆弧纯弯，最大变形量为0.333 mm，与仿真获得的变形结果接近。通过式(19)计算获得校正该变形所需的校正力矩为24 652.5 N·mm，对应的压入量约为0.020 mm。滚压校正完成后，工件最大变形量为0.060 mm，相对于初始加工变形降低82.0%。

与仿真获得的变形消除率相比，试验过程仍然存在较大误差。对载荷预测和试验过程进行分析，误差来源主要包括以下几个方面：① 试验中滚轮压入量采用直线位移传感器控制，只能保证压入过程中的压入量，在滚压过程中随着滚轮转动压入量可能会存在误差；② 压入量计算过程采用了大量有限元仿真结果，将校正力矩换算为压入量时存在计算误差；③ 在等效刚度计算过程中，采用了有限元方法计算工件弯曲变形量，存在仿真误差。

图10 滚压校正前后变形量对比
Fig.10Comparison of deformation before and after rolling correction

图11 滚压校正前后表面残余应力变化
Fig.11Variation of surface residual stress before and after rolling correction

图11给出了特征点表面的残余应力测试数据。铣削表面以残余拉应力为主，经过滚压操作，滚压区域的应力转变为残余压应力，x方向和z方向最大压应力分别达到-55.1 MPa和-101.8 MPa。在z方向，压应力引起侧壁顶部滚压区域材料向z轴正方向流动，对工件整体变形影响较小。在x方向，工件发生弯曲变形，在滚压和变形综合作用下分别使点P2、P3、P4的表面拉应力增大9.3%、7.2%和3.4%。

滚压区域材料在滚轮的碾压作用下发生塑性变形伸长，周围材料在其拉伸作用下产生了附加拉应力。但是，工件整体引入的残余拉应力并不显著，说明滚压校正过程对工件疲劳寿命的影响较小，具有较高的安全性。此外，通过残余应力的测量，间接说明了工艺参数的合理性。

4 结 论

1) 通过对校正过程所满足的能量平衡方程进行分析，结合弯曲应变能法和等效惯性矩法，建立了变形量与校正力矩的数学模型，形成了梁类航空整体结构件滚压变形校正载荷预测方法。

2) 采用直接应力法建立了加工变形-滚压校正协同仿真环境，实现了梁类航空整体结构件滚压校正的快速仿真分析，提供了校正载荷预测准确性的快速评价方法，仿真分析获得的三隔框整体结构件变形消除率为94.5%。

3) 进行了三隔框整体结构件滚压变形校正试验，工件最大变形量从0.333 mm降低到0.060 mm，相对于初始加工变形消除率达到82.0%，验证了该方法的正确性。

[1] 孙杰， 李剑峰， 王中秋， 等. 航空整体结构件加工变形控制与校正关键技术[J]. 航空制造技术, 2009(23): 62-66.

SUN J, LI J F, WANG Z Q, et al. Key technology on processing deformation control and correction of aviation overall parts[J]. Aeronautical Manufacturing Technology, 2009(23): 62-66 (in Chinese).

[2] MASOUDI S, AMINI S, SAEIDI E, et al. Effect of machining-induced residual stress on the distortion of thin-walled parts[J]. The International Journal of Advanced Manufacturing Technology, 2015, 76(1-4): 597-608.

[3] YANG Y, LI M, LI K R. Comparison and analysis of main effect elements of machining distortion for aluminum alloy and titanium alloy aircraft monolithic component[J]. The International Journal of Advanced Manufacturing Technology, 2014, 70(9-12): 1803-1811.

[4] 杨吟飞， 张峥， 李亮， 等. 7085铝合金残余应力及加工变形的数值仿真与试验[J]. 航空学报, 2014, 35(2): 574-581.

YANG Y F, ZHANG Z, LI L, et al. Numerical simulation and test of bulk residual stress and machining distortion in aluminum alloy 7085[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(2): 574-581 (in Chinese).

[5] MASOUDI S, AMINI S, SAEIDI E, et al. Effect of machining-induced residual stress on the distortion of thin-walled parts[J]. The International Journal of Advanced Manufacturing Technology, 2015, 76(1-4): 597-608.

[6] MA Y, FENG P, ZHANG J, et al. Prediction of surface residual stress after end milling based on cutting force and temperature[J]. Journal of Materials Processing Technology, 2016, 235: 41-48.

[7] HUANG X, SUN J, LI J. Effect ofinitial residual stress and machining-induced residual stress on the deformation of aluminium alloy plate[J]. Strojniški Vestnik-Journal of Mechanical Engineering, 2015, 61(2): 131-137.

[8] 张峥. 飞机弱刚性铝合金结构件的残余应力和加工变形控制技术研究[D]. 南京: 南京航空航天大学, 2015.

ZHANG Z. Research on residual stress and machining distortion of aeronautic weak rigidity in aluminum structure[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015 (in Chinese).

[9] 黄晓明， 孙杰， 李剑峰. 基于刚度与应力演变机制的航空整体结构件加工变形预测理论建模[J]. 机械工程学报, 2017, 49(9): 201-208.

HUANG X M, SUN J, LI J F. Mathematical modeling of aeronautical monolithic component machining distortion based on stiffness and residual stress evolvement[J]. Journal of Mechanical Engineering, 2017, 49(9): 201-208 (in Chinese).

[10] CHANTZIS D, VAN-DER-VEEN S, ZETTLER J, et al. An industrial workflow to minimise part distortion for machining of large monolithic components in aerospace industry[J]. Procedia CIRP, 2013, 8: 281-286.

[11] LI B, JIANG X, YANG J, et al. Effects of depth of cut on the redistribution of residual stress and distortion during the milling of thin-walled part[J]. Journal of Materials Processing Technology, 2015, 216: 223-233.

[12] 刘长青. 基于动态加工特征的航空结构件智能加工关键技术[D]. 南京: 南京航空航天大学, 2014.

LIU C Q. The Key technologies of intelligent machining based on dynamic machining feature for aerospace structural parts[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014 (in Chinese).

[13] 孙杰. 航空整体结构件数控加工变形校正理论和方法研究[D]. 杭州: 浙江大学, 2003.

SUN J. Study oncorrection theory and method for distorted aeronautical monolithic component due to NC machining[D]. Hangzhou: Zhejiang University, 2003 (in Chinese).

[14] 张洪伟， 张以都， 吴琼， 等. 基于有限元仿真的航空整体结构件变形校正[J]. 北京航空航天大学学报, 2007, 33(10): 1251-1255.

ZHANG H W, ZHANG Y D, WU Q, et al. Straightening technique for distorted aeronautical monolithic component based on finite element numerical simulation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(10): 1251-1255 (in Chinese).

[15] 张洪伟， 张以都， 吴琼， 等. 航空整体结构件加工变形校正技术研究[J]. 兵工学报, 2010, 31(8): 1072-1077.

ZHANG H W, ZHANG Y D, WU Q, et al. Research on deformation straightening for aeronautical monolithic components[J]. Acta Armamentarii, 2010, 31(8): 1072-1077 (in Chinese).

[16] PERENDA J, TRAJKOVSKI J, ŽEROVNIK A, et al. Residual stresses after deep rolling of a torsion bar made from high strength steel[J]. Journal of Materials Processing Technology, 2015, 218: 89-98.

[17] LIU Y, ZHAO X, WANG D. Determination of the plastic properties of materials treated by ultrasonic surface rolling process through instrumented indentation[J]. Materials Science and Engineering: A, 2014, 600: 21-31.

[18] DING H, WANG Y, CAI L. Laser shock forming of aluminum sheet: Finite element analysis and experimental study[J]. Applied Surface Science, 2010, 256(6): 1703-1707.

[19] 王中秋. 航空整体结构件加工变形滚压校正理论及方法研究[D]. 济南: 山东大学, 2009.

WANG Z Q. Study on theory and approach for correcting aerospace monolithic component due to machining distortion using rolling method[D]. Jinan: Shandong University, 2009 (in Chinese).

[20] LU L, SUN J. Investigation on distortion mechanism and correcting load calculation method for aluminum beam structure by bilateral rolling process[J]. Procedia CIRP, 2016, 57: 781-786.

[21] LU L, SUN J, LI Y, et al. A theoretical model for load prediction in rolling correction process of thin-walled aeronautic parts[J]. The International Journal of Advanced Manufacturing Technology, 2017, 92(9-12): 4121-4131.

[22] S.铁摩辛柯, J.盖尔. 材料力学[M]. 胡人礼, 译. 北京: 科学出版社, 1978.

TIMOSHENKO S, GERE J. Mechanics of materials[M]. HU R L, translated. Beijing: Science Press Ltd., 1978 (in Chinese).

[23] 刘鸿文. 材料力学Ⅰ[M].5版. 北京: 高等教育出版社, 2010.

LIU H W. Mechanics of materials Ⅰ[M]. 5th ed. Beijing: China Higher Education Press, 2010 (in Chinese).

[24] 张炜， 刘立彬， 夏明莉， 等. 机翼缘条喷丸强化变形模拟与参数优化[J]. 航空制造技术, 2016(17): 28-32.

ZHANG W, LIU L B, XIA M L, et al. Simulation and optimization of shot peening deformation for aircraft wing flange[J]. Aeronautical Manufacturing Technology, 2016(17): 28-32 (in Chinese).

Loadpredictionmethodofrollingdistortioncorrectionformonolithicaeronauticalcomponentsbasedonenergytheory

LULaixiao1,SUNJie1,*,HANXiong2,XIONGQingchun2,SONGGe2

1.KeyLaboratoryofHighEfficiencyandCleanMechanicalManufactureofMinistryofEducation,SchoolofMechanicalEngineering,ShandongUniversity,Jinan250061,China2.AVICChengduAircraftIndustrial(Group)Co.,Ltd.,Chengdu610092,China

MonolithicaeronauticalcomponentshavevaryingdegreesandformsofmachiningdeformationduetothecouplingeffectofvariousfactorsinNumericalControl(NC)machining.Rollingoperationisaneffectivemeanstocorrectdistortionoflargeaspectratiothin-walledstructures,andcompressivestressisintroducedtoimprovetheservicelifeandobtainthedimensionalaccuracyoftheworkpiece.Atpresent,rollingcorrectiondependsmainlyonthetrialanderrormethodbasedonworkers'experience,andlackofaccuratepredictionmethodforthecorrectedloadleadstopoorqualitystability.Inthispaper,therequirementforenergybalanceofabeamstructureisanalyzed.Theequivalentsectionmethodandthebendingstrainenergymethodareusedtocalculatethebendingstrainenergyandtherollingintroducedenergy,respectively.Then,amathematicalmodelforworkpiecedistortionandcorrectionloadisestablishedtopredictthecorrectionload.Toachieverapidevaluationofaccuracyofthecorrectionload,thecollaborativesimulationenvironmentofmachiningdistortion-rollingcorrectionisestablishedbythedirectstressmethodtorealizefast-equivalentsimulationofdeformationofmonolithicaeronauticalcomponents.Thethree-frameintegralstructureisusedasanexampletoverifythatthedistortioneliminationrateobtainedbythesimulationwiththedirectstressmethodis94.5%.Theexperimentalresultsshowthatthedistortioneliminationrateofsinglerollingis82.0%,andthesurfaceoftherollingareaischangedfrommillingtensilestresstorollingcompressivestress.Thecorrectioneffectisinlinewithexpectations.

monolithicaeronauticalcomponent;rolling;distortioncorrection;loadprediction;finiteelementmethod

2017-04-14；

2017-05-08；

2017-06-16；Publishedonline2017-07-311114

URL：http://hkxb.buaa.edu.cn/CN/html/20171229.html

NationalNaturalScienceFoundationofChina(51275277)

.E-mailsunjie@sdu.edu.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.421326

2017-04-14；退修日期2017-05-08；录用日期2017-06-16；网络出版时间2017-07-311114

http://hkxb.buaa.edu.cn/CN/html/20171229.html

国家自然科学基金(51275277)

.E-mailsunjie@sdu.edu.cn

路来骁，孙杰，韩雄，等．基于能量理论的航空整体结构件滚压变形校正载荷预测方法J． 航空学报,2017,38(12):421326.LULX,SUNJ,HANX,etal.LoadpredictionmethodofrollingdistortioncorrectionformonolithicaeronauticalcomponentsbasedonenergytheoryJ.ActaAeronauticaetAstronauticaSinica,2017,38(12):421326.

V261.2+6

A

1000-6893(2017)12-421326-09

李世秋)