自由活塞激波风洞的入射激波衰减
朱浩,江海南,张冰冰
中国航天空气动力技术研究院,北京 100074
自由活塞激波风洞的入射激波衰减
朱浩*,江海南,张冰冰
中国航天空气动力技术研究院,北京 100074
自由活塞激波风洞产生的入射激波在行进过程中存在较大衰减,这种现象不仅降低了风洞喷管贮室的焓值、压力的量值和平稳性,而且也制约了风洞有效试验时间。针对自由活塞激波风洞结构特点,试图揭示入射激波衰减的主导原因。在忽略一些偶然性随机性因素后,重点对黏性衰减和反射膨胀波作用两个因素的影响进行了分析和比较。结果表明,在风洞主膜片打开时刻,活塞前脸与主膜片之间的短促距离,加剧了反射膨胀波的影响,在很多情况下,这是导致激波衰减的更为主要的因素。出于降低激波衰减和延长风洞有效试验时间的实际工程需要,提出了变截面活塞压缩器的设计构型。随后的理论研究显示,该构型能够实现活塞充分减速并达到安全速度,被压缩气体(驱动气体)能够形成平稳的压力/温度平台,满足激波管驱动需要。
自由活塞激波风洞;入射激波;衰减;压缩管;安全速度
高超声速飞行一般伴随着“真实气体”效应的产生。为了获得更为精确的飞行器流场和热环境数据,地面试验设备应当能够忠实于飞行环境,产生“真实气体”效应。当前,由于理论与数值计算的局限性,地面试验仍然是研究“真实气体” 效应的主要手段之一。
激波风洞采用氢气或者氦气作为驱动气体(室温),可以在试验段获得焓值为5 MJ/kg左右的试验气体(空气);而利用加热器加热氢气或者采用氢氧混合气体在氦气中燃烧的办法,可使试验气体焓值增加到12.5 MJ/kg左右[1]。在此量级的焓值之下,氧气将发生显著的离解,而氮气的离解则可忽略。为了获得更高焓值的试验气流,则要依靠自由活塞激波风洞,这类风洞的运行特点是,利用重活塞的快速等熵压缩,实现对驱动气体(主要是氦气-氩气的混合气体)的加热加压,用以驱动激波管获得高强度激波[2]。随着对高超声速飞行兴趣的增长,美国和其他西方国家近年来陆续兴建这类自由活塞激波风洞,例如澳大利亚的T4、美国的T5、德国的HEG、以及日本的HIEST均是这类风洞的代表[3-9]。
图1 自由活塞激波风洞示意图
Fig.1 Skematic of free piston shock tunnel
自由活塞激波风洞气动/结构设计以获取高焓试验气流作为最高目标,这类风洞一个主要的设计特点是:压缩管和激波管直接相连,主膜片紧靠压缩管末端(参见图1)。从理论上看,截面的突然收缩有助于提高风洞的驱动压力,获得更高的入射激波强度(相比等截面激波管而言)。在实际运行中,自由活塞激波风洞面临的一个重要问题是,入射激波在行进过程中衰减很大,这使得试验气体的焓值/压力很难达到预期的量值和平稳性,同时风洞的有效试验时间也受到很大的制约。自由活塞激波风洞中激波衰减的事实为研究者所熟知,但是长期以来,对其成因缺少深入的研究和定量的分析,这一情况妨碍了自由活塞激波风洞气动设计的改进和优化。在忽略一些偶然性因素后,本文着重分析比较了边界层黏性和反射膨胀波作用这两个因素对激波衰减的影响。研究结果表明,多数情况下,反射膨胀波是导致激波衰减更为主要的因素。其原因在于,风洞主膜片打开时刻,活塞前脸与主膜片之间的距离过于短促,这是自由活塞激波风洞传统构型的固有结果。为了有效缓解激波衰减,并延长风洞有效试验时间,本文提出一个变截面构型活塞压缩器的设计构型,并从理论上论证了这种设计的可行性。
1 激波衰减结果和比较
在自由活塞激波风洞中,入射激波的衰减对喷管贮室中试验气体状态影响显著。导致激波衰减的因素较多,分析不同的影响因素对风洞的设计和运行有重要意义。总体而言,激波在行进过程中的衰减机制十分复杂,膜片打开的非理想过程、激波管内径大小及内壁粗糙程度、边界层黏性、反射稀疏波的作用等都可能导致衰减。基于自由活塞激波风洞的结构特点,本文专注于边界层黏性和反射稀疏波的作用两个主要因素的研究和比较。
边界层黏性主导的激波衰减就曾受到不少研究者的注意。Mirels[10]和Trimpi[11]认为,在完全湍流边界层情况下,激波的衰减和激波管直径成反比。Emrich[12]和Spence[13]等先后引入波后雷诺数刻画激波强度的衰减。针对不同的驱动气体和被驱动气体,Anderson和Murthy[14]依据小扰动理论,采用不同指数律形式的速度型和密度型,获得了由边界层而引起的激波衰减的进一步结果。特别地,根据文献[13],真实气体条件下,激波速度的保持率可以表述为

(1)
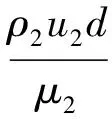
为了便于分析,本文以文献[16]提供的T4风洞的第2 499次发射作为算例,比较了数值模拟、式(1)和测量值之间的差别,其结果见表1。表1中ST2d是一套基于平衡气体假设的二维激波管计算程序,以轴对称Navier-Stokes方程作为流动控制方程,对流通量计算格式为AUSM+ (Advection Upstream Splitting Method)格式,湍流模型为Spalart-Allmaras模型,时间推进格式为LU-SGS (Lower Upper Symmetric Guass Seidel)隐式格式。程序中使用的气体热力学性质由文献[17]提供的拟合函数给出。另外,L1d程序的细节参见文献[16]。表1的结果显示:① ST2d程序获得的激波行进速度与L1d程序计算值及测量值之间差异很小,具有很高的可靠性。② 在该运行条件下,激波衰减严重。 ST2d和L1d程序获得的激波速度保持率约为0.69。式(1)中常系数C的取值为0.07或0.097 7时,边界层黏性主导的激波衰减率分别为0.11和0.16, 偏差较小。③ 除了边界层黏性以外, 还存在其他因素使得激波出现严重的衰减,甚至强于边界层黏性所带来的影响。

表1 激波速度衰减对比
2 反射膨胀波所导致的激波衰减
在自由活塞激波风洞中,当活塞对驱动气体的压缩结束时,活塞的停止位置与膜片之间的距离十分靠近,致使驱动段与被驱动段长度之比很小(通常不足1/10)。另一方面,为了获得更强的驱动效果,风洞采用轻质气体(主要是氦气或者氦/氩混合气体)作为驱动气体,在经过重活塞压缩以后,驱动气体的声速十分可观,这使得膜片破裂时形成的稀疏波具有很高的传播速度。在上述两个因素的共同影响下,稀疏波迅速抵达活塞前脸并发生反射,之后很快地追赶上接触面(甚至激波),并与之发生相互作用。我们推测这一现象是导致入射激波严重衰减的另外一个重要原因。对普通的反射型激波风洞而言,驱动段长度大约是被驱动段长度的1/2左右,较长的驱动段使得稀疏波反射和追赶行为大大延迟。这就是说,反射稀疏波所导致的激波衰减一般不会在这类反射型激波风洞中出现,此时的激波衰减主要由边界层黏性引起。为了进一步证实上述猜测,采用ST2d程序对不同的设计构型进行了数值模拟。为了便于比较和校验,仍然采用文献[16]中的另外一个运行状态No.1 089,被驱动段的内径和长度不变,仅仅改变驱动段的内径和长度,具体计算参数和结果参见表2。表中4个条件均采用100%的氦气作为驱动气体,压力为57 MPa,温度为4 543 K,空气作为被驱动气体,压力为100 kPa,温度为296 K。
表2的结果显示:① 在1-2、1-4条件下(对应长驱动段),激波的衰减仅由边界层黏性引起,此时激波速度下降约2%。② 在1-1、1-3条件下(对应短驱动段),激波的衰减由边界层黏性和反射膨胀波作用共同引起,而反射稀疏波引起的衰减比黏性引起的衰减更为严重。驱动段越短,反射稀疏波引起的激波衰减也就越突出。③ 与1-3、1-4等截面驱动结果相比,1-1的变截面技术带来了激波速度的增加,但是由于驱动段很短,不足以抵消反射稀疏波引起的激波衰减,以至激波的最终速度仍然低于1-3、1-4条件下的。
图2展示了表2中4种不同条件下的激波管中轴线上压力分布,以及接触面(Contact Surface,CS)/激波速度随时间的变化,更加细致地刻画了反射膨胀波引起激波衰减的过程,图中横坐标l为沿激波管轴向的坐标,其以主膜片为坐标原点。特别地,在1-1的条件下,反射稀疏波在激波管下游2 m附近,即追赶上接触面与之发生作用,在此以后接触面/激波一直处于明显的减速状态。而在1-3的条件下,由于驱动段长度增加,反射稀疏波追赶上接触面的位置后移(约在激波管下游4 m处附近)。在1-2和1-4条件下,反射稀疏波未曾追赶上接触面,因此接触面保持缓慢的加速,激波在黏性下缓慢减速,这一变化趋势和文献[18]的试验结果一致。
结合上述两个方面的研究,我们得到如下结论:在自由活塞激波风洞中,边界层黏性和反射稀疏波的作用是导致入射激波衰减的两个重要因素,而后者的影响可能更为剧烈,其原因在于风洞主膜片打开(压缩结束)时刻,活塞前脸十分靠近主膜片,导致反射膨胀波过早地追赶上接触面/激波并与之发生相互作用。另外,数值计算暗示,驱动气体中氩气的加入可以推迟反射稀疏波和接触面/激波的相互作用时间,但是缓解程度有限。

表2 不同驱动段长度下的激波速度衰减Table 2 Attenuation of shock wave velocity with different length of driver sections
图2 不同驱动段长度下的压力分布、接触面速度和激波速度
Fig.2Pressure distribution, contact surface velocity, and shock wave velocity with different length of driver sections
3 传统构型的改进
图3 变截面自由活塞压缩器方案
Fig.3 Conceptual design of free piston compression tube with an abrupt area change
为了缓解反射稀疏波引起的激波衰减,延长风洞有效试验时间,并最终提升风洞的驱动效果,本文基于上述理论研究结果,提出了一种变截面活塞压缩器的设计方案(见图3)。在这种设计方案中,压缩管采用变截面结构(前段为粗段,后段为细段),激波管内径的选择则具有一定自由度,可以等于或者大于压缩管细段内径。主膜片位置处于压缩管细段与激波管连接位置。在相同的压缩比下,这种结构旨在增加活塞停止位置和主膜片之间的距离(即实际激波管驱动段的长度)。变截面压缩管粗段与细段的容积之比大于实际运行时的压缩比(前者约为后者1.2~1.7倍为宜)。另外,图3中的主膜夹持机构可以通过变更主膜片的位置获得不同压缩比。对变截面压缩管而言,活塞仅在压缩管粗段中行进,这意味着在压缩结束阶段,活塞必须在更短距离上完成减速抵达设备允许的安全速度,这是该设计方案具有应用价值的关键。
在图3的变截面压缩管中,假定压缩管粗段的长度和直径分别为L1和D1,压缩管细段的长度和直径分别为L2和D2,活塞质量为Mp。假定高压空气贮室的初始压力为pA,0,初始声速为aA,0,被压缩气体(激波管的驱动气体)的初始压力pHA,0。活塞在运动过程中任意时刻的受力为

式中:x为活塞位移(以活塞起点为原点,x (2) 式中:up为活塞的瞬时速度;γA为空气的比热比。式(2)是假定活塞和它所在的初始位置相孤立,产生的膨胀波不发生反射。同时,在膜片破裂以前,活塞的前脸所受压力pHA表示为 (3) (4) 式中:aHA,0为驱动气体的初始声速。 在参数空间(b1,b2)求解式(3)和式(4)即可获得活塞运动的具体细节和总体特征。当被压缩气体为氦气时,在固定压缩比λ=30,40,50下,图4给出了活塞在压缩管粗段末端抵达安全速度(≤20 m/s)时最可能的参数集合(图中红色区域)。这意味着,在一定的人工摩擦的干预下,活塞可以在压缩管粗段末端达到安全速度,并和缓冲装置发生接触。活塞压缩器的实际运行状态将在这个参数集合内进一步挑选产生(结合活塞调谐操作与设备结构)。图4中计算所对应的变截面压缩管尺寸以及若干参数点所对应的末端速度/位移见表3。若被压缩气体采用氩气/氦气混合气体,其声速较氦气小,在主膜片打开以后,混合气体下泄速率减小,腔内背压下降相对缓慢,活塞更容易减速并抵达安全速度。因此,这种设计方案具有良好的可行性,值得进一步试验研究。 图4 活塞抵达安全速度所对应的参数集合(红色区域) 
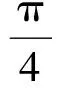
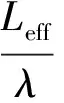

Fig.4 Feasible region on parameter plane to obtain safe velocity of piston (red region)

λScaleofcompressiontube/mL1D1L2D2MaxcompressionratioCoordinates(b1,b2)Finalvelocity/(m·s-1)Finaldistance/m30400.5560.1863.2(0.027,28.8)0.3439.5840400.5560.1863.2(0.021,26.5)0.3539.7050400.5550.1875.7(0.019,24.0)0.3339.84
4 驱动性能
图5 压缩管末端压力与温度的分布
Fig.5Distributions of pressure and temperature at end of compression tube
在压缩管中,被压缩气体压力/温度的增加主要是通过压缩波作用实现的。较长的压缩管细段使得压缩波传播行程增加,有可能会降低压缩管细段的压力/温度分布均匀性。为此,本文进行了多次的数值模拟研究(假定活塞满足调谐操作),数值计算显示这种结构对压缩管细段的压力/温度分布均匀性影响微弱,最大的不均匀性出现在截面突然变化的区域,图5是众多算例中较有代表性的一个。这个算例对应的初始条件是:压缩管粗段直径为0.5 m,长度为25 m,压缩管细段直径为0.16 m,长度为10 m,压缩管初始填充压力pDr,0=0.165 9 MPa,活塞驱动压力pA,0=25pDr,0,活塞质量为200 kg。通过图5可以看出,随着活塞向前推进,压缩管细段中的被压缩气体压力/温度逐渐升高,均匀性逐渐增加,高压力/温度平台逐步形成,且平稳性优良,足以满足驱动激波管运行的需要。另外,根据文献[20]的相关试验研究结果,对于压缩管末端被压缩气体压力可能出现的某些高频扰动波,变截面活塞压缩器较长的细段将有助于抑制这一现象的发生。
表2中算例1-1实际对应着传统自由活塞压缩器驱动的激波管,而算例1-4对应着变截面活塞压缩器所驱动的激波管(此时压缩管细段内径刚好等于激波管内径)。在这两个算例中,驱动段容积十分接近(暗示驱动气体质量接近)。因此这两个算例的相关对比结果,体现了理想情况下变截面压缩器的优势。具体地说,在相同压缩比和驱动气体组分、压力和温度下,虽然变截面活塞压缩器驱动的激波管获得的入射激波速度弱于传统自由活塞压缩器驱动的激波管,但是由于变截面活塞压缩器驱动的激波管有效抑制了激波衰减,在激波管末端,激波速度仍比传统情况要高出不少。
根据激波风洞长期的运行经验,对变截面活塞压缩器而言,压缩管细段内的驱动气体压力/温度将存在一定的损失。在膜片打开时刻,压缩管细段中被压缩气体压力/温度将低于传统活塞压缩器相应值,这是采用变截面压缩器需要付出的代价。截面突然变化区域出现的流动分离和复杂波系是导致压力损失的主要原因。以下仍将结合算例1-1和1-4,在计及压力损失情况下,简单地评估变截面活塞压缩器可能获得的驱动性能的提升。
在理想情况下,膜片打开时刻变截面压缩管末端压力和温度分别为pDr,r和TDr,r(即理想情况下的驱动压力p4和温度T4),根据临界条件及等熵关系,压缩管细段入口处的气体压力p*和温度T*满足
(5)
根据表2中驱动气体的状态,可得到p*=
0.487pDr,r=27.767 MPa,T*=3 407.25 K。实际运行中,激波管驱动段内的驱动气体平均压力p4,real通常满足
p* (6) 若以p*和T*作为驱动气体压力和温度的下限,根据激波关系式,计算得到入射激波速度US,0real为2.955 km/s(被驱动气体参数见表2)。式(1)表明,在激波管几何尺寸相同的前提下,激波衰减程度和激波速度正相关。另外,根据经典激波管理论,在相同激波管尺寸和驱动/被驱动气体组分下,激波速度越弱,膨胀波追赶上接触面的时间越滞后。因此,在算例1-4的几何尺寸下,当驱动气体压力温度降低时,激波衰减仅由黏性引起,且衰减水平低于算例1-1,于是可以知道激波末端速度US,freal不小于2.955×0.975≈2.88 km/s,该值仍大于算例1-1下的激波末端速度2.812 km/s。这个极端情况暗示,如果压力损失使得压缩完成时刻驱动气体压力下降为理论值的0.487倍(温度按照等熵关系折算),那么激波末端速度将增加得不多,但是反射稀疏波到达激波管末端的时间却将大为延迟。 假若认为,激波管驱动段内驱动气体的实际压力和温度接近如下几何平均值 (7) 则经过简单的计算可得到p4,real=0.698pDr,r,T4,real=0.866TDr,r。在这个驱动状态下,入射激波速度US,0real=3.374 km/s,略低于1-4条件下的理论值US,0=3.50 km/s,其激波的末端速 度也应满足US,freal≥3.374×0.975=3.290 km/s,该值比算例1-1中的末端速度高出约17%。而反射膨胀波的不利影响也将得到相应的延迟。 1) 在自由活塞激波风洞中,激波的衰减主要由边界层黏性和反射膨胀波引起,在多数情况下,后者的影响可能处于主导地位。在压缩结束时刻,活塞前脸与主膜片之间的短促距离,是导致反射膨胀波产生影响的根本原因。 2) 变截面驱动带来的增益,通常不足以补偿反射膨胀波引起的激波衰减,传统自由活塞激波风洞的理论设计构型需要作出适当调整。 3) 变截面活塞压缩器的构型有利于减缓激波的衰减,延长风洞有效试验时间。在这种构型下,活塞可以获得充分减速;压缩结束前后被压缩气体(驱动气体)具有平稳的压力/温度平台,可以满足激波管驱动要求。 4) 在实际运行中,变截面活塞压缩器驱动的激波管存在一定的压力损失,只要驱动气体压力损失控制得当,其焓值仍将明显高于传统自由活塞激波管。 [1] GAI S L. Free piston shock tunnels: Developments and capabilities [J]. Progress in Aerospace Sciences, 1992, 29(1): 1-41. [2] STALKER R J. A study of the free piston shock tunnel [J]. AIAA Journal, 1967, 5 (12): 2160-2165. [3] STALKER R J. Shock tunnel for real gas hypersonic: AGARD-CP-428[R]. Brussels: AGARD, 1987. [4] STALKER R J. Modern developments in hypersonic wind tunnels[J]. Aeronautical Journal, 2006, 110 (1103): 21-39. [5] STALKER R J, MORGAN R G. The University of Queensland free piston shock tunnel T-4: Initial operation and preliminary calibration[C]∥4th National Space Engineering Symposium. Barton, ACT: Institute of Engineers, Australia, 1988:182-198. [6] HORNUNG H.Performance data of the new free-piston shock tunnel at GALCIT: AIAA-1992-3943[R]. Reston, VA: AIAA, 1992. [7] EITELBER G, MCINTYRE T J, BECK W H, et al. The high enthalpy shock tunnel in Göttingen: AIAA-1992-3942[R]. Reston, VA: AIAA, 1992. [8] EITELBERG G. First results of calibration and use of HEG: AIAA-1994-2525[R]. Reston, VA: AIAA, 1994. [9] ITOH K.Characteristics of the HIEST and its applicability for hypersonic aerothermodynamic and scramjet research[M]∥Advanced Hypersonic Test Facilities. Reston, VA: AIAA, 2002:239-253. [10] MIRELS H. Attenuation in a shock tube due to unsteady- boundary-layer action: NACA TN 3278[R]. Washington, D.C.: NACA, 1956. [11] TRIMPI R L. Nonlinear theory for predicting the effects of unsteady laminar, turbulent, transitional boundary layers on the attenuation of shock wave in a shock tube:NASA TN 4347[R]. Washington, D. C.: NASA, 1958. [12] EMRICH R J, WHEELER D B. Wall effect in shock tube flow [J]. Physics of Fluids, 1958, 1(1): 14-23. [13] SPENCE D A, WOODS D A. Boundary layer and combustion effects in shock tube flows[J]. Hypersonic Flows, 1960, 11(3): 163-180. [14] ANDERSON G F, MURTHY V S. Attenuation of the shock in a shock tube due to effect of wall boundary layer: AIAA-1968-0053[R]. Reston, VA: AIAA, 1968. [15] MUYLAERT J, VOIRON R, SAGNIER G, et al.Review of the European hypersonic wind tunnel performance and simulation requirements[C]∥Proceedings of the First European Symposium on Aerothermodynamics for Space Vehicles. 1991: 559-574. [16] JACOBS P A. Quasi-one-dimensional modeling of free piston shock tunnel[J]. AIAA Journal, 1994, 32(1): 137-145. [17] SRINIVASAN S, TANNEHILL J C. Simplified curve fits for the thermodynamic properties of equilibrium air:NASA-CR-178411[R].Washington, D. C.: NASA, 1987. [18] DOOLAN C J. Modeling mass entrainment in a quasi-one-dimensional shock tube code[J]. AIAA Journal, 1996, 34(6): 1291-1293. [19] HORNUNG H G.The piston motion in a free piston driver for shock tubes and tunnels: GAL.CIT Rep. FM88-1 [R]. Pasadena, CA: California Institute of Technology, 1988. [20] LABRACHERIE L, DUMITRESCU M P, BURTSCHELL Y, et al. On the compression process in a free-piston shock-tunnel[J]. Shock Waves, 1993, 3(1): 19-23. Attenuationofincidentshockwavesinfreepistonshocktunnels ZHUHao*,JIANGHainan,ZHANGBingbing ChinaAcademyofAerospaceAerodynamics,Beijing100074,China Attenuationofincidentshockwavesinfreepistonshocktunnelsisofgreatimportant,whichnotonlyreducestheenthalpy,pressureandsteadiness,butalsoimposesconstraintsonvalidtestingtime.Inthisstudy,anattemptofinvestigationofmainreasonsofattenuationofshockwavewascarriedoutbasedonthestructuralfeaturesoffreepistontunnels.Afterneglectingsomerandomfactors,twoimportantfactorsofattenuation,viscosityoftheboundarylayerandthereflectedexpansionwave,werestudied.Theresultsshowthatthelatterfactorplaysmajorroleinfreepistonshocktunnels.Whenthemaindiaphragmruptures,thefrontfaceofthepistonisveryclosetothemaindiaphragm,whichleadstoreflectedexpansionwavetocatchupwiththeinterfaceorshockwaveearlier.Anewcompressiontubewithanabruptareachangewasproposed,whichcandelaytheinteractionbetweenthereflectedexpansionwaveandtheinterface(orshockwave).Inthenewcompressiontube,thesteadypressureandtemperatureofdrivergascouldbeformedintheendofthetubewhilethefreepistondeceleratedtoasafetyspeed. freepistonshocktunnel;incidentshockwave;attenuation;compressiontube;safevelocity 2017-04-17; 2017-06-20; 2017-07-14;Publishedonline2017-07-201554 URL:http://hkxb.buaa.edu.cn/CN/html/20171204.html NationalNaturalScienceFoundationofChina(11572303) .E-mail13439821690@163.com http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn 10.7527/S1000-6893.2017.121328 2017-04-17;退修日期2017-06-20;录用日期2017-07-14;网络出版时间2017-07-201554 http://hkxb.buaa.edu.cn/CN/html/20171204.html 国家自然科学基金(11572303) .E-mail13439821690@163.com 朱浩,江海南,张冰冰.自由活塞激波风洞的入射激波衰减J. 航空学报,2017,38(12):121328.ZHUH,JIANGHN,ZHANGBB.AttenuationofincidentshockwavesinfreepistonshocktunnelsJ.ActaAeronauticaetAstronauticaSinica,2017,38(12):121328. V211.751 A 1000-6893(2017)12-121328-09 王娇)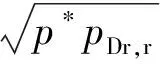
5 结 论

