基于SOA算法的EHB制动系统压力控制研究

吴学杰，冯智勇，裴晓飞，危 刚，孙道远

（武汉理工大学 现代汽车零部件技术湖北省重点实验室，武汉 430070）

基于SOA算法的EHB制动系统压力控制研究

吴学杰，冯智勇，裴晓飞，危 刚，孙道远

（武汉理工大学 现代汽车零部件技术湖北省重点实验室，武汉 430070）

为了对电控液压制动系统（EHB）制动压力进行精确控制，该文根据制动系统结构和性能特点，建立数学模型；基于丰田Prius车型的EHB液压单元，进行开环增减压试验，验证模型精确性；在此基础上，基于模型开发轮缸变参数增量式PID控制算法。蓄能器线性增压阶段，压力产生超调，对系统压力控制产生较大影响，因此该文采用人群搜索算法（SOA）对蓄能器压力控制器参数进行迭代寻优。搭建EHB试验台架，对比仿真和台架试验对阶跃、三角波、正弦3种期望压力信号的跟踪效果，验证轮缸增量式PID压力控制算法与蓄能器SOA参数整定后的控制算法对制动压力控制的精确性。结果表明轮缸压力控制算法和参数整定后的蓄能器压力控制算法具有较高的控制精确性和鲁棒性。

电控液压制动系统；控制器；试验台架；人群搜索算法

汽车的制动效能是影响行车安全最关键的因素。传统制动系统由驾驶员作用于制动踏板，将踏板力经过机械和液压系统传递，作用于轮缸，对车辆进行制动，由于机械和液压系统的滞后特性，会对制动距离和制动减速度产生较大影响，引起交通安全问题。电控液压制动系统以电子元件取代部分机械和液压元件，具有响应快、可靠性高等特点，并且减轻了整车质量。本文针对丰田Prius车型的电控液压制动系统（EHB）的液压单元（HCU）进行建模，基于模型采用改进的增量式PID控制算法对轮缸压力进行控制[1]；为防止蓄能器充液过程中产生较大超调，本文以液压单元的电机为控制对象，设计PID控制器，稳定而快速地对蓄能器进行充液，并且基于人群搜索算法（SOA），以误差绝对值和输入量平方的时间积分作为评价指标，经过一系列的迭代寻优得到PID控制器3个参数的最优值[2]。与此同时进行EHB台架试验，对比仿真和台架试验的结果，验证控制算法对轮缸压力控制效果。

1 EHB制动系统结构及性能特点

基于丰田Prius车型的EHB制动系统结构简图如图1所示。

图1 丰田Prius车型的EHB制动系统结构Fig.1 Toyota Prius models of EHB brake system structure

制动系统有2种建压方式，一种为传统制动，即通过制动踏板，经制动主缸、电磁切换阀a、b、FL增压阀、FL减压阀，在两前轮缸中建立压力；另一种为EHB制动模式，即关闭电磁阀a、b，踏板模拟器模拟驾驶员制动脚感，踏板位移传感器将踏板位移信号传入ECU，由ECU判断驾驶员制动意图，并且计算出轮缸的期望压力。压力传感器a始终监测高压蓄能器内部压力，当压力小于预定压力时，电机泵启动，向蓄能器内充液，使蓄能器始终保持高压状态。压力跟随控制器根据控制策略，控制轮缸增减压电磁阀和电机泵的开闭，保持轮缸压力精确跟随期望压力，并且使蓄能器始终保持高压状态。

2 EHB制动系统数学建模

EHB制动系统液压单元，主要包括直流电机、固定排量油泵、高压蓄能器、电磁阀、制动轮缸等主要部分，故可对EHB液压系统进行模块化建模。

2.1 直流电机数学模型

根据基尔霍夫电压和电磁定律可得：

式中：U为电机两端电压；Rm为电枢电阻；Lm为电枢感抗，数值很小可忽略不计；Kf为复合黏性摩擦系数；Jm为电机转子转动惯量；Tload为电机负载转矩；Kv为反电动势系数；w为电机转速；Kt为转矩系数，Kt=Kv。

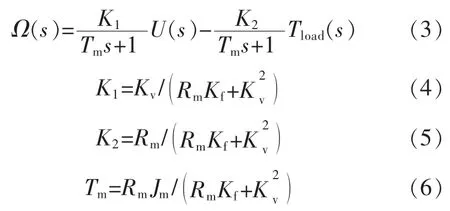
对于电机的实际工作环境来说，当负载转矩大于电机转矩时电机不可能反转。所以电机角速度可用式（7）描述：

2.2 油泵数学模型建模

式中：q为泵流量；P为泵两端液体的压力差；Pp、Pt分别为蓄能器的压力和储液壶的压力，即油泵两端压力；T为油泵的输入转矩，即电机的负载转矩；D为泵的排量；ω为泵的转动角速度；kleak为油泵泄露系数；kHP为哈根-泊素叶系数；ηv为油泵容积效率；ηmech为油泵机械效率；v为制动液运动学粘度；ρ为制动液密度；ρnom为公称密度；Pnom为油泵额定压力；ωnom为油泵额定角速度；vnom为制动液公称运动学粘度[3]。

2.3 蓄能器数学模型建模

式中：VF为进入蓄能器液体体积；VA为蓄能器容积；Vpr为预载液体容积；P为蓄能器出口压力；Ppr为预载液体压力；Pa为大气压；Ks为进口压力系数；k为气体多变指数[4]。

2.4 电磁阀数学模型建模

2.4.1 电磁回路建模

电磁阀与轮缸示意如图2所示。

图2 电磁阀与轮缸示意Fig.2 Schematic diagram of solenoid valve and the wheel cylinder

式中：Φ为磁通量；vsol为电磁线圈的电压，这里即为车载电压；R为电磁阀电阻；N为线圈匝数；B为磁通密度；A为气隙的横截面积；μ0为空气的导磁系数；Hair、Hsteel分别为空气中的磁场强度与铁芯的磁场强度[5]。

磁场强度和磁通密度的非线性关系如图3所示。

图3 磁场强度H和磁通密度B的非线性关系Fig.3 Nonlinear relationship of H magnetic field strength and magnetic flux density B

式中：MF为磁动势；g为气隙的长度；Lsteel为铁芯的长度；i为电磁回路中的电流；Fsol为电磁力。

2.4.2 电磁阀液压流量特性分析

电磁阀示意如图4所示。

图4 电磁阀示意Fig.4 Solenoid valve

式中：qnet为进入轮缸的制动液流量；qex为从球阀与阀座缝隙中泄露的制动液流量；qs为从蓄能器进入电磁阀阀口处的流量；Pc为电磁阀后的制动液压力；A0为电磁阀口开度的横截面积；K0为制动液流量系数。

2.4.3 电磁阀动力学分析

电磁阀阀芯的动力学平衡方程为[3]

式中：A0为阀口当量横截面积；Ps为蓄能器内制动液压强；Fs0为弹簧预载压力；Ks为弹簧胡克系数；Cv为阻尼率。

2.5 制动轮缸数学模型建模

轮缸工作原理示意图如图5所示。

图5 轮缸工作原理示意Fig.5 Wheel cylinder working principle diagram

综合以上各式可得：

式中：β为体积弹性模量，一般通过试验来测定；ε1为流量的变化量；ε2轮缸内体积变化率；dPc为轮缸内的压力变化量；Ap为轮缸横截面积。

2.6 EHB制动器数学模型验证

基于丰田Prius车型的EHB液压单元对制动系统数学模型进行开环验证，结果如图6、图7所示。

图6 蓄能器压力验证Fig.6 Accumulator pressure test and verify

图7 蓄能器增压和减压试验验证Fig.7 Accumulator charging and reducing test

通过对蓄能器增压和轮缸增减压开环验证可以看出，EHB系统蓄能器在线性增压阶段出现超调，制动系统数学模型的建立总体比较准确。

3 轮缸压力控制器和蓄能器压力控制器设计

轮缸压力控制器和蓄能器压力控制器决定了电控压力控制系统对期望压力的跟随特性，其控制性能将直接影响汽车制动效能和行车安全性。

轮缸压力控制算法在增量式PID控制算法的基础上做出改进，主要有以下几点：

（1）以某一阈值为切换条件，进行PI控制和PD控制，并且根据压差大小，设置不同的控制参数。

（2）系统需要在增、减、保压3种不同的状态下进行切换，所以每次切换都需要对增量式PID进行清零操作。

（3）积分是对微小误差的累积，但是微小误差经过长时间累积，可以使电磁阀的控制量变大，所以当积分操作达到某一阈值时，需要及时清零，以防止对控制效果产生不良影响[6]。

蓄能器压力控制采用PID控制算法，并且基于人群搜索算法（SOA），以压力差绝对值和控制输入量的平方项对时间的积分为控制目标，对PID控制器的3个控制参数进行迭代寻优。

制动系统控制策略如图8所示。

图8 EHB系统控制策略Fig.8 EHB system control strategy

4 基于SOA算法的蓄能器PID控制器设计

4.1 PID控制器离散化

对于蓄能器压力控制，主要体现在对电机转速的控制。空载时，电机如果转速不稳定，启动时产生较大的超调，引起震动，会对电磁阀开闭以及压力传感器对信号采集的精确度产生较大的影响。因此需要利用PID控制器对电机转速进行控制[7]。PID控制规律为

对其进行离散化处理：

4.2 SOA参数整定设计方案

4.2.1 SOA算法原理

SOA算法模拟人的寻优行为，即当人的搜索接近位置最优值时，缩小搜索范围，当搜索位置较差时，应该扩大搜索范围，通过模仿人类寻优的经验梯度和不确定性推理来搜索问题的解。SOA算法的PID参数整定原理如图9所示。

图9 基于SOA算法的PID参数整定原理Fig.9 Based on SOA PID parameter setting principle diagram of the algorithm

4.2.2 PID控制参数编码

令搜寻种群P中的个体数为30，每个个体由3个元素构成，所以该种群P可由一个30×3的矩阵表示为

4.2.3 适应度函数值求解

搜索个体结果的优劣以适应度值的大小来评判，适应度值越小，搜索结果越理想，并且适应度值也是搜索步长确定和位置更新的依据。适应度函数值采用式（34）计算[8]：

为了避免蓄能器线性增压阶段电机转速出现较大超调，因此需要采取惩罚控制，即一旦出现较大的超调量，期望值与实际值的误差将在适应度值的求解中占有较大的比例。此时的适应度函数为

如果 e（k）＜0 则：

式中：ω1、ω2、ω3为权值，通常 ω3≫ω1。

4.2.4 搜索步长的确定

对适应度值F进行降序排列，作为模糊推理的输入。利用模糊系统的逼近能力，确定适应值与步长之间的关系[9]。

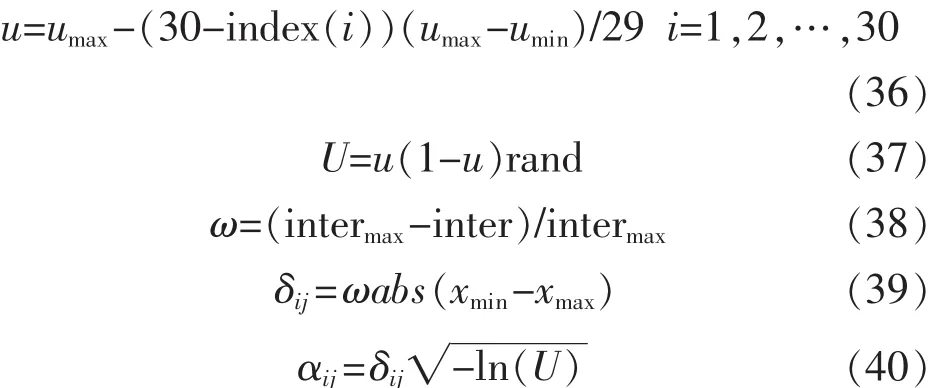
式中：u为隶属度；umax、umin分别为最大隶属度和最小隶属度；U为对应适应度值的隶属度；index（i）为适应度值排列后的位置；inter为当前迭代次数；intermax为最大迭代次数；ω为高斯隶属度参数的权值；δij为高斯参数；αij为搜索步长。

4.2.5 寻优方向的确定

4.2.6 个体位置的更新

当寻优的步长和方向确定后，需要进行搜索位置的更新。

式中：xij（t）为寻优种群 P 的个体。

4.2.7 电动机仿真及结果分析

通过计算，得出电机空载时的传递函数为

式中：K1=1.18；Tm=5.5×10-2；U（s）为电机电压；Ω（s）为电机转速。

对电机传递函数进行离散化，离散时间间隔为ts=0.001 s得：

期望转速为300 rad/s，参数优化及仿真结果如图10～图12所示。

图10 个体最优适应度值Fig.10 Optimal individual fitness value

图11 PID参数整定结果Fig.11 PID parameter setting

图12 电机转速阶跃响应Fig.12 Motor speed step response

从图10中可以看出适应度值比较小，大约为9.88，说明SOA优化算法的精度比较高。图11为Kp、Ki、Kd经过 100 次迭代后的整定结果，Kp=13.4，Ki=13，Kd=0。图12为电机期望转速为300 rad/s的阶跃响应，电机大约在0.07 s时转速达到280 rad/s，2 s末时转速大约为300 rad/s，并且没有出现超调，响应较快，控制效果很好。

5 仿真与台架试验结果对比验证

通过搭建电控液压制动系统试验台架，并且对阶跃、三角波、正弦期望压力进行跟随，与仿真试验进行比对验证轮缸压力控制算法和蓄能器PID参数整定的有效性[11]，试验结果如图13～图15所示。

图13 阶跃压力跟随对比Fig.13 Step pressure following

图14 三角波压力跟随对比Fig.14 Triangle wave pressure following

图15 正弦压力跟随对比Fig.15 Sinusoidal pressure following

阶跃压力跟随试验中，台架试验和仿真试验轮缸响应很快，并且超调量很小，蓄能器压力并没有出现较大波动，对增减压电磁阀的开闭和压力传感器的信号采集精度影响较小。三角波和正弦压力跟随试验中，期望压力的变化率相对较小，台架试验和仿真试验的轮缸与蓄能器的压力跟随结果没有出现明显偏差，跟随结果比较理想。

6 结语

为了提高对系统制动压力的精确控制，本文针对电控液压制动系统（EHB）的结构和性能特点，建立制动系统液压单元数学模型，在此基础之上，设计针对轮缸压力控制的分段变参数的增量式PID控制器，并且为防止蓄能器充液时压力出现较大超调，应用人群智能搜索算法SOA对蓄能器PID控制器的控制参数进行整定，观察整定后的电机转速对阶跃信号的响应，结果比较理想。对比电控制动系统台架试验和仿真试验对阶跃、三角波、正弦3种期望压力的跟随效果，验证控制器的效果，试验结果表明，经过参数整定后的控制器具有较好的控制精度和鲁棒性。

[1] 李寿涛，马用学，郭鹏程.基于电控液压制动系统的车辆稳定性控制策略[J].吉林大学学报：工学版，2015，45（2）：526-532.

[2] 郭鹏程.汽车电控液压制动系统建模及控制算法研究[D].吉林：吉林大学汽车工程学院，2015.

[3] 汪洋，魏民祥.基于联合仿真的EHB系统轮缸压力模糊PID控制研究[J].公路与汽运，2010（6）：12-15.

[4] DaiC，Chen W，Zhu Y.Seekeroptimization algorit-hm[C]//InternationalConference on ComputationalIntelligence and Security，IEEE，2006：225-229.

[5] 李静，杨雄，苗卉.基于台架试验的电控液压制动系统动态特性[J].吉林大学学报：工学版，2016，46（1）：15-20.

[6] 马国成，刘昭度，裴晓飞，等.汽车自适应巡航控制主动制动实现方法[J].北京理工大学学报，2012，32（2）：120-124.

[7] Xu.S，Z.Yu，L.Xiong.Controlofnovelintegrated-electrohydraulic brake system for automotive[J].See Brake Colloquium&，Exhibition，2015.

[8] 余胜威，曹中清.基于人群搜索算法的PID控制器参数优化[J].计算机仿真，2014，31（9）：347-350.

[9] H Yeo，C Koo，W Jung，et al.Development of smart booster brake Systems for regenerative brake cooperative control[J].Sae Brake Colloquium&Engineering Display，2011.

[10]孟杰，陈庆樟，张凯.基于粒子群算法的汽车悬架PID控制仿真[J].计算机仿真，2013，30（4）：155-168．

[11]黄伟中，郭立书，施正堂，等.基于电控液压制动的电动汽车制动动态响应[J].吉林大学学报：工学版，2012，42（S1）：13-16.

Research on Pressure Control of EHB Braking System Based on SOA Algorithm

WU Xue-jie，FENG Zhi-yong，PEI Xiao-fei，WEI Gang，SUN Dao-yuan
（Hubei Key Laboratory of Advanced Technology for Automotive Components，Wuhan University of Technology，Wuhan 430070，China）

In order to control the brake pressure of the electronic hydraulic braking system（EHB），the mathematical model is established according to the structure and performance characteristics of the braking system.Based on the EHB hydraulic unit of the Toyota Prius model，open-loop pressurization and decompression test is done.Based on the model，develop wheel cylinder variable parameter incremental PID control algorithm.In this paper，the seeker optimization algorithm（SOA） is used to optimize the parameters of the accumulator pressure controller.In order to comparing effectiveness of simulation and bench that follow the expect pressure of step，triangle wave，sine signal，the EHB test bench is built.Validation of wheel cylinder pressure of incremental PID control algorithm and the accumulator after the SOA parameters setting of brake pressure control precision of the control algorithm.The results show that the pressure control algorithm and the accumulator pressure control algorithm have high control accuracy and robustness.

electronic hydraulic braking（EHB）；controller；test bench；seeker optimization algorithm（SOA）

TP274

A

1001-9944（2017）11-0049-07

10.19557/j.cnki.1001-9944.2017.11.012

2017-04-11；

2017-07-24

国家自然科学青年基金资助项目（61503290）

吴学杰（1991—），男，硕士研究生，研究方向为汽车电控及主动安全技术；冯智勇（1981—），男，博士，副教授，硕士生导师，研究方向为控制理论、汽车电控。