退火算法与神经网络算法结合在路径规划中的研究
李江伟,许伦辉
(华南理工大学 土木与交通学院,广州 510641)
退火算法与神经网络算法结合在路径规划中的研究
李江伟,许伦辉
(华南理工大学 土木与交通学院,广州 510641)
路径规划问题是计算机、数学、交通、机器人等包含了众多领域在内的经典问题,它可以被描述为一个最优化问题。为了解决经典算法在求解最优路径时运算时长的问题,该文研究了神经网络和模拟退火算法的特点,建立了一般路网的数学模型;根据神经网络和模拟退火算法的特点设计了适合车辆诱导的路网最优路径算法。结果表明,应用神经网络算法和模拟退火算法相结合,比单独使用任何一个算法的效率高。
路径规划;神经网络;模拟退火算法
一个网络中,在满足一定的约束条件下,找出一条从任意2点之间的最优路径,可以是时间少、距离最短,也可以是费用最低,或者有多个优化目标,考虑这几种因素的综合影响。路径规划在很多领域都有着非常广泛的应用,例如交通、物流、通信系统的路由搜索、机器人行走路线规划等,以及近两年非常热门的无人机,路径规划算法已成为其最为关键的核心技术之一。路径规划问题可以表示为一个数学上的多目标优化问题,因此在路径规划问题就转化为求解相应的数学优化问题。在此,重点研究利用合适的方法求解最优解。
最短路径问题是网络优化中的一个最基本的也是最重要的分支,同时也是所有路径规划问题的基础。许多路径规划问题都可以转化为这样的最短路径问题模型来表达,或者可以用最短路算法作为子程序。

为路径的权值,是特定情况下的约束条件,研究的目的就是在约束条件下求得目标函数的最小值。在实际的交通路网中,路段或者节点的数量都是非常多的,求解的复杂度较高,需要找到一种既能够较好地找到全局最优解,又有着较快的运算速度的方法。因此,提出了一种基于模拟退火-Hopfield神经网络的算法(SA-CHNN),并利用神经网络的高度并行性,借助并行计算技术来提高算法的计算速度,且能够有效地求得全局最优解。
1 模拟退火算法
1.1 退火算法原理
模拟退火是一种随机的搜索方法,其灵感来自于退火的过程。它的基本思想是,首先将温度设置为一个足够高的水平,此时绝大部分的随机运动方向都是可行的,可以在比较大的空间内找到一个目标值相对低的区域;随着温度根据一定的规则慢慢降低,各个方向被选中的概率会变得不一样,当然搜索的精度也不断提高。模拟退火算法的更新迭代过程主要用到MetroPolis准则,具体如下:
①假设状态在xk时,当使用一定的扰动对系统进行影响,使状态发送变化,得到一个新的状态xk+1,前后两个状态对应的系统能量分别为E(xk)和E(xk+1),能量差为ΔE;
②ΔE≤0,则转换为状态 xk+1;
③ΔE≥0,则转换为xk+1的概率为
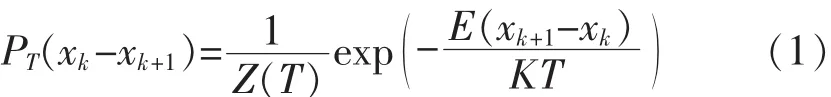
式中:K为波尔兹曼常量;T为温度;Z(T)为规范化因子。
④设 r=random(0,1)为(0,1)上的随机数,与 Pr进行比较。若Pr≥r则接受新状态,反之状态维持不变。
温度较高时可以接受较大的能量差,温度下降到一定的程度后,只有较小的能量差被接受。利用这一思想,当各个条件满足的时候,也就是值达到了最优解。通过类比上述的物理过程,可以得到优化问题的解MetroPolis准则,目标函数为xk和xk+1的解,则由xk转换到xk+1的接受概率为式中:T为退火过程中的温度值。T0为算法迭代过程开始时的起始温度,初始解为x=x0。在算法迭代的过程中不断产生新解,根据上述准则判断接受新解的概率判断是否接受。随着迭代的进行,温度T下降,直至满足收敛条件,算法收敛时就可以得到最优解。

通过随机的方法来产生新的解[1]。假设当前解为,候选解为。当前解xi的某一个分量在一定领域内进行随机变化,产生出新的值,候选解xi+1的计算公式为
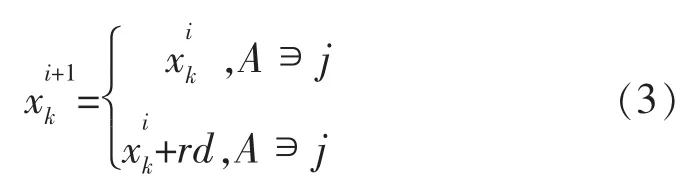
式中:r为区间[-1,1]的随机数;d为领域调整因子。在连续模拟退火算法的开始阶段,d可以取较大值,目的是使d能够在较大范围内进行搜索,然后再逐渐减小d,缩小搜索范围。常取d为线性函数d=ηd,其中0<η<1。此外,新产生的候选解必须满足优化问题的约束条件。当满足式(3)的2个条件的时候,候选解也可以采取以下形式[2]:
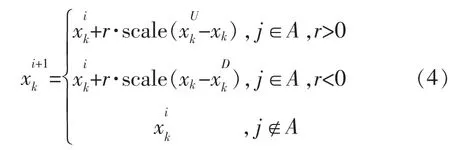
1.2 参数的设置
在利用模拟退火算法求解优化问题,尤其是非凸优化问题时,参数设置是否合理在很大程度上影响到算法的性能。虽然从理论上来说,只要初始温度够高、下降速度够慢、迭代次数够多,算法就能以1的概率收敛于全局最小值。但是在实际的应用中,不可能花费近乎无限的时间来等待结果,只要求算法能够在合理的时间内给出满足精度的解。为了满足精度和效率的要求,需要对模拟退火算法的几个主要参数进行分析设计并合理设置大小。
1)初始温度T0的选择
初始温度T0是算法开始阶段的系统温度。模拟退火算法在迭代早期需要在比较大的范围内进行搜索,也就是说此时的算法接受新解的概率非常高,所以初始温度需要取得比较大,使得exp(-Δ f/T0)接近于1,能进行全局性、大范围的搜索。实践表明,当初始的温度越高时,获得高质量解的可能性也越大,这使得算法从一开始就达到准平衡的状态,否则退火过程将变成局部搜索的过程,只能得到低质量的解。然而,过大的初始温度又会导致算法效率的下降,需要非常长的迭代过程才能收敛。T0的具体取值,要在实际应用过程中根据实验结果进行适当调整,总的原则是在保证效率能够接受的情况下,尽可能提高初始温度。
2)Markvo链长度 Lk的设置
Markvo链长度Lk是在某温度T下的总迭代次数,用于控制生产的候选解的数量。要达到热平衡状态,Lk不能太短。理论上,Lk与温度下降速度有关,如果温度下降越快,就需要越长的Markov链,以确保模拟退火算法能够搜索到全局最优解。一般地,Lk取定值L=100d比较合适,式中d为优化向量的维度。
3)温度下降函数的选择
为避免算法产生过长的Markov链,系统温度T的下降速度都比较小,这也是选取温度下降函数的一个重要原则。应用中,使用最多的是线性下降函数Tk+1=αTk,式中α为小于1但接近1的数,一般取α=0.95~0.98之间,用于控制温度下降的速率。除此之外,还有许多不同的降温方案,如经典退火、快速退火、超快速退火等。
4)算法终止的条件
在理论上,模拟退火算法必须在温度足够接近0或者解不在发生变化时才能停止。合适的终止条件,不但能够保证算法在多项式时间内收敛于某一近似解,而且能使最终解具有较高的质量。根据研究经验,常用的终止条件有以下2种:
①温度下降到冷却阈值以下;
②经过多次降温,当前最优解一直无法得到进一步改善等。
1.3 计算示例
求解Camel函数的全局最优点,所求问题的数学模型为

式中:Camel函数含有 2 个自变量,在区间 x∈[-3,3],y∈[-2,2]上有6个局部极小值点,其中有对称的全局极小值点,为(0.0898,-0.7126),由其取得全局极小值为1.31628。
采用C++编写模拟退火算法。CPU为i5-5200U,内存12 G,设置初始温度T0=30,去掉 Markvo链Lk=200,降温速率α=0.98,领域范围内取定值scale=0.05,初始点为(2,1)。
针对2种不同的终止条件进行测试。第1种条件,温度下降到终止温度Te=0.001后,系统达到平衡后也就达到最优解,则算法结束;第2种条件,连续k次降温最优解不在发生变化时,算法结束,取k=200。优化结果见表1。

表1 退火算法优化结果Tab.1 Simulated annealing algorithm optimization results
2 退火算法与Hopfield神经网络结合
2.1 算法结合原理
虽然模拟退火算法具有很强的全局搜索能力,而且不要求目标函数为凸函数,它能够以一定概率接受次最优解,使得算法在迭代过程中不会像Hopfield神经网络一样陷入局部最优。理论上只要有初始的系统温度够高、温度下降够慢、迭代次数够多,算法收敛于全局最优解的概率即为100%。但是,也是由于模拟退火算法是一种随机性的算法,在效率上还有一定欠缺,单纯使用模拟退火算法尚存在一定问题。
按照网络输出值的类型,一般将神经网络划分为离散型(DHNN)和连续性(CHNN)2种不同的类型[3],这2种类型的Hopfield神经网络原理是一致的。在此主要研究连续性神经网络。Hopfield神经网络具有快速收敛的特性,而且因其网络结构并具有高度的并行性,适合于进行并行化或者分布式的计算,能够大幅度提高算法的运行速度。由于其在整个迭代过程中,能量函数只能沿着减小的方向变化,这一特点决定了Hopfield神经网络在解决非凸优化问题时很可能会陷入局部最优,最终所得到的解与初始点的设置关系密切,不容易得到全局最优解[4]。因此,可以将两者有效结合起来求解优化问题,能够较为快速地得到全局最优解,将该方法命名为SA-CHNN[5]。
使用SA-CHNN求解全局最优化问题时,仍以CHNN为主,利用CHNN找到1个极小值点时,再用模拟退火算法在对此极小值点的领域进行若干次的搜索;Markov链的长度可以定得比较大,以确保能够跳出局部最优。然后,继续使用CHNN寻优,不断循环,如果经过若干次如次循环仍未找到比当前更优的解,则该点即作为全局极小值点。
根据Hopfield神经网络理论,将优化问题中的变量 x(x∈R)神经网络的输出 v(v∈R)相对应起来,就可以将优化问题映射到CHNN中去。利用罚函数的思想将有约束的优化模型转换为无约束的函数:


由于原始的CHNN的神经元输出值被限制于[0,1]之间,但在优化问题中,许多变化的范围超出这个界限,为了对神经元节点的sigmoid的函数进行定义:
根据网络CHNN的迭代方程就可以对网络进行迭代更新,当网络收敛于稳定状态时,神经元的输出值就是相应优化问题的解。
对于递归网络函数来说,稳定性是一个非常关键的指标,决定了网络能否收敛到一个稳定状态。目前使用最多的Hopfield提出的lyapunov函数[6],定义如下:
式中:δ-1为 δ(.)的反函数,一般来说 τ会取一个很大的值,所以能量函数中积分项的值会非常小,故网络能量函数也可以写为
通过对上述公式中能量函数进行分析,可以很容易得到Hopefield神经网络的重要参数,包括连接权重和偏置。ωr的比例因子分别为ky=kz=35/6。

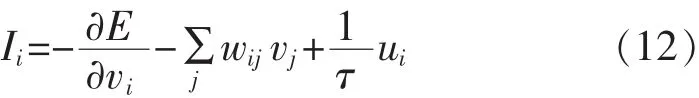
如果一个优化问题可以表示为上述公式,那么就可以利用Hopfield神经网络来求解这个优化问题,得到相应的解。Hopefield和Tank在1985年发表的论文中指出,如果需要利用Hopefield神经网络来求解优化问题,那么能量函数必须是一个可收敛的函数[7],并给出了证明。算法流程如图1所示。
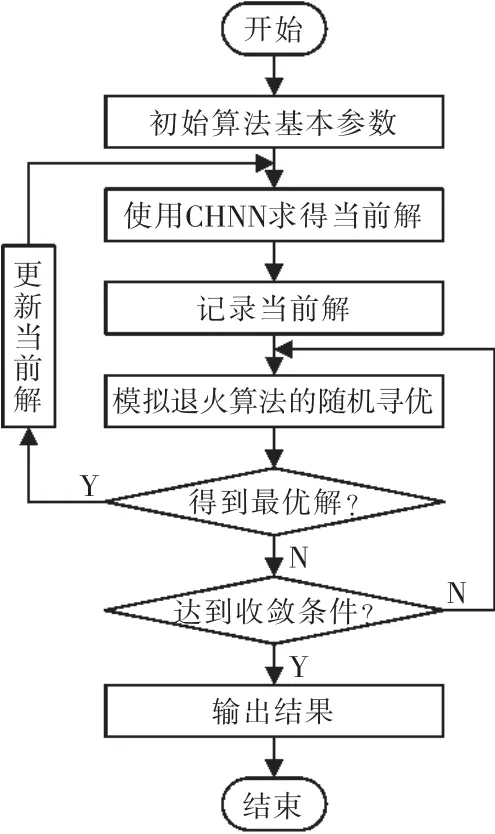
图1 算法流程Fig.1 Algorithm flow chart
2.2 计算示例
仍以选取Camel函数为例对SA-CHNN进行验证[5]。 设置 CHNN 的神经元个数为 2,η=200,sigmoid函数调节参数 λ=0.01,更新步长 step为 0.01,τ=5000,收敛条件 ΔE<10-6。 起点 x0=(2,1)T网络能量函数为
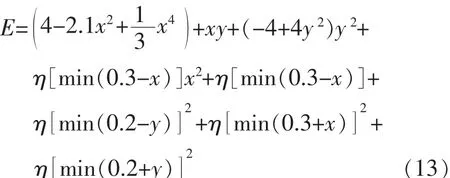
设置模拟退火算法的初始温度T0=30,取Markvo链 Lk=200,降温速率 α=0.98,领域范围因子 scale=0.05,收敛条件为模拟退火经过200次。
应用算法,可以得到运行结果,算法从初始点(2,1)开始执行,使用CHNN进行迭代,收敛于局部极小值点(1.601,0.574);使用模拟退火算法的随机性搜索,并跳出该局部极小值点,以这个点作为CHNN的初始点再次进行迭代,收敛于另一个极小值点(1.698,-0.799)。SA-CHNN算法不断进行“寻优—陷入局部最优—跳出—再次寻优”的迭代过程,直到模拟退火算法无法找到最好的解,可以得到算法收敛于点(0.901,0.7111)。该点即为全局最小值点,最小值为1.6026,运行时间 0.688 s。
2.3 结果对比
通过退火算法得到的最优结果为1.6163,耗时1.319 s;通过算法融合得到的最优值为1.6026,耗时0.688 s。在结果相差不大的情况下,后者较前者快了近1/2,结果的对比见表2。
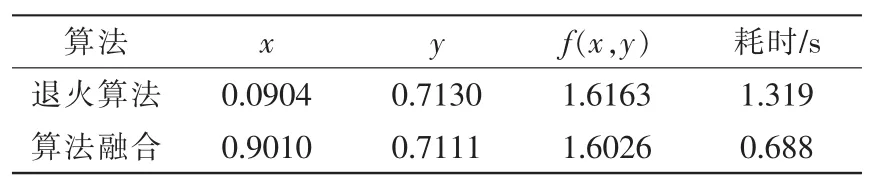
表2 不同算法的结果对比Tab.2 Results comparison of different algorithms
3 结语
针对Hopfield神经网络在求解非凸优化问题上的局限性,将其与连续性的模拟退火算法进行相结合,利用其局部优化能力求解非凸优化问题,并用算例对这一算法进行了验证。结果表明,神经网络与退火算法相结合,即克服了Hopfield神经网络求解非凸优化问题的局限性,又比单用模拟退火算法的效率高。
[1] 江加和,宋子善,沈为群,等.模拟退火算法在连续变量全局优化问题中应用[J].北京航空航天大学学报,2001,27(5):556-559.
[2] 罗亚中,唐国金.两层非线性规划问题的并行模拟退火全局优化[J].系统仿真学报,2005,17(5):1040-1044.
[3] 王林山.时滞递归神经网络[M].北京:科学出版社,2008.
[4] Ghatee M,Mohades A.Motion planning in order to optimize the length and clearance applying a hopfield neural network[J].Expert Systems with Applications,2009,36(3):4688-4695.
[5] 张华烨.基于神经网络的路径规划并行算法的设计与实现[D].广州:华南理工大学,2013.
[6] 张捍东,郑睿.岑豫皖.移动机器人路径规划技术的现状与展望[J].系统仿真学报,2005,17(2):439-443.
[7] 陈科.基于并行思维的设计理念和设计方法研究[D].合肥:合肥工业大学,2001.
Research on Path Planning Based on Simulated Annealing Algorithm and Neural Network Algorithm
LI Jiang-wei,XU Lun-hui
(School of Civil Engineering and Transportation,South China University of Technology,Guangzhou 510641,China)
The problem of path planning is a classical problem including computer,mathematics,traffic,robot and so on.It can be described as an optimization problem.In order to solve the problem of long operation time of classical algorithm in solving optimal path,the characteristics of neural network and simulated annealing algorithm are studied,and the mathematical model of general road network is established.According to the characteristics of neural network and simulated annealing algorithm,the optimal path algorithm for vehicle guidance is designed.The results show that the combination of neural network algorithm and simulated annealing algorithm is more efficient than any single algorithm alone.
path planning;neural network;simulated annealing algorithm
TP273.4
A
1001-9944(2017)11-0006-04
10.19557/j.cnki.1001-9944.2017.11.002
2017-04-20;
2017-09-25
李江伟(1990—),男,硕士研究生,研究方向为交通运输工程;许伦辉(1965—),男,教授,博士生导师,研究方向为智能控制理论及应用、智能交通系统等。

