基于双目视觉的双臂模糊轨迹跟踪控制

王 勇 ，刘 治

（1.广东工业大学 自动化学院，广州 510006；2.广东外语外贸大学 教育技术中心，广州 510420）

基于双目视觉的双臂模糊轨迹跟踪控制

王 勇1，2，刘 治1

（1.广东工业大学 自动化学院，广州 510006；2.广东外语外贸大学 教育技术中心，广州 510420）

在双目视觉系统的监视下，双臂系统夹持目标执行视觉轨迹跟踪任务。随意的目标夹持姿态引起的动力学不确定性会影响控制性能，尤其目标质量较大时。因此，该文在控制器设计中引入模糊系统来逼近系统的动力学特征。同时，采用分散控制策略解决双臂系统的运动学和动力学协同问题，然后在位置/力混合控制的框架下设计了基于双目视觉的双臂模糊轨迹跟踪控制器。最后，通过仿真证明了控制器的有效性。

双臂系统；双目视觉伺服；位置/力混合控制

机器人是计算机技术、机器视觉、自动控制和传感器等多种技术融合的载体，近年来随着人工智能的快速发展，机器人在工业生产方面发挥着越来越重要的作用。同时，在生活服务方面的应用也越来越多。与单臂机器人相比，多臂机器人具有功能丰富灵活的特点，可以完成复杂的家务劳动，同时，可以代替人类从事复杂危险的工作。因此多臂机器人一直是机器人领域的研究热点，其研究的重点和难点就是多臂之间的协同控制问题。当多个末端执行器夹紧目标对象时将会形成运动学闭链，在目标运动过程中，目标与末端执行器之间的相对位姿要保持不变。同时，还需控制目标和系统中的内应力，避免破坏目标和系统。

在多臂系统协同控制方法中，位置/力混合控制是常用的控制方法之一。由于位置控制和力控制存在正交性特点，因此通过2个控制环路分别实现位置和力的控制。在动力学建模方面，由于目标和机械臂耦合在一起，因此精确建模十分困难，为此引入模糊系统和神经网络来解决此问题[1-8]。

由于相机具有非接触和信息量丰富的优点，因此在控制领域被广泛使用，且发展出了视觉伺服控制方法。根据误差定义的不同，视觉伺服一般可分成两类：分别是基于图像的视觉伺服[9-13]和基于位置的视觉伺服[14-16]。因此本文在双臂控制中引入双目视觉系统，研究基于视觉的双臂协同控制方法。首先采用模糊系统解决随意夹持姿态引起的动力学不确定问题，然后在位置/力混合控制框架下，采用分散控制策略设计了基于双目视觉的模糊轨迹跟踪控制器，并且通过仿真验证了控制方法的有效性，同时此方法还可应用于一般的多机械臂系统。

1 双目视觉模型

如图1所示，双目视觉系统由2个内参数完全相同的针孔相机构成。相机1坐标系Σc1和相机2坐标系Σc2的 x 轴，xc1和 xc2同轴同向，同时 zc1和 zc2平行且同向。另外，原点oc1和oc2之间的距离是b。

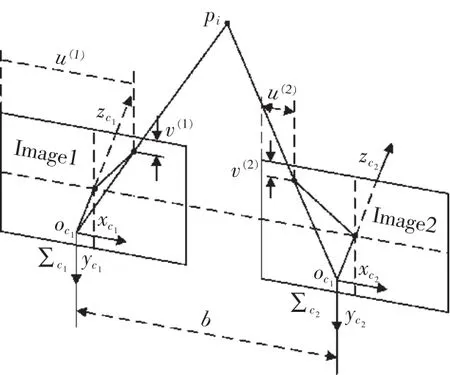
图1 双目视觉模型Fig.1 Binocular vision model

式中 ：M（k）表示 相 机 k 的参 数；表 示特 征 点 pi在相机k坐标系下的深度。由于双目视觉系统中相机特殊的位置配置，有

对式（1）求导可得特征点pi在相机k的图像平面上的速度为

2 运动学

目标在双臂的夹持下进行运动，在世界坐标系下，根据前向运动学可以得到

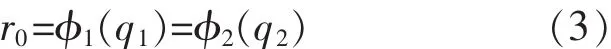
式中：r0∈RN表示目标质心坐标；No表示目标的自由度；qj∈RNq表示机械臂 j的关节向量，j=1，2；Nq表示机械臂j的关节自由度。对式（3）求导可得目标质心速度与关节速度的关系为

式中：I3×3表示3阶单位矩阵；Λci表示由特征点 pi与目标质心的相对距离构成的矩阵，详见文献[16]。

Z=diag（z1，z1，…，zNp，zNp），式（6）可以写成

3 动力学

根据拉格朗日方法建立机械臂j的动力学方程为

式中：Hj（qj）∈RNq×Nq表示机械臂 j的正定惯性矩阵；Cj（qj，q˙j）∈RNq×Nq表示哥式力和向心力矩阵；Gj（qj）∈RNq表示重力向量；Fej表示目标作用在执行器j上的作用力；τj表示机械臂j上的驱动力。另外，对目标可建立如下动力学方程：

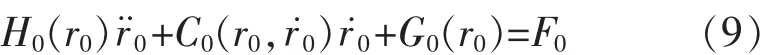
式中：H0（r0）∈RNo×No表示目标物体的正定惯性矩阵；C0（r0，˙0）∈RNo×No表示目标的哥式力和向心力矩阵；G0（r0）∈RNo表示重力向量；F0表示双臂对目标的作用合力。根据机械臂j的受力分析可以得到：

式中：Fcej表示目标质心对末端执行器j的作用力。根据力的合成与分解，目标受到的合力为

另外，根据力对目标运动的影响，Fcej可以分解成：

式中：fj表示机械臂j与目标之间的内应力；foj表示作用于目标运动的力，并且有：

将式（11）和式（12）带入式（9）可得：

假设在t时刻机械臂j分担负载的情况用函数cj（t）表示，那么 foj可以写成：

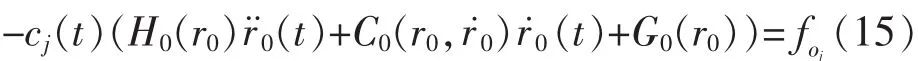
因此，机械臂j耦合目标的动力学方程可以写成

式中：Hj（qj）=Hj（qj）+cj（t）H0（qj）；

4 控制器设计

4.1 参考变量

特征点pi在图像平面k上的理想位置，理想速度和理想加速度分别用和表示，那么特征点pi在图像平面k上的参考速度定义为

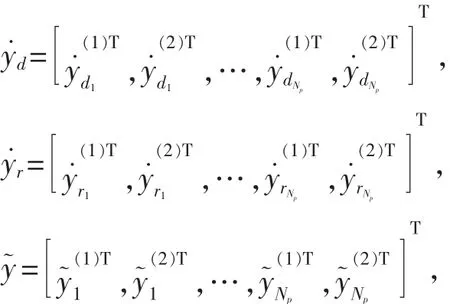
式（17）可写成：

同时，机械臂j关节空间的参考速度定义为

4.2 模糊系统

目标对象的动力学不确定性会引起控制性能下降，甚至出现系统不稳定的情况，因此控制设计中引入模糊逻辑系统逼近系统的动力学特征。定义模糊逻辑系统，根据模糊规则可以将和写成如下形式

综上，在位置/力混合控制框架下，采用分散控制策略，基于双目视觉的双臂模糊轨迹跟踪控制器设计如下：

式中：KΦj∈RNl1×Nq是正定矩阵，i=1，2。

5 仿真

为了证明上文提出的控制器的有效性，在Matlab平台上进行仿真验证。双臂系统由2个完全相同的三关节机械臂构成，机械臂1的基坐标系与世界坐标重合，机械臂2的基坐标系原点在世界坐标系下坐标是（1，0，0）T，其姿态与机械臂 1 的基坐标系相同。

相机参数如表1所示，控制器设计中的参数和控制增益设置为 λ＝1.5，Ks1＝Ks2＝diag（10，10，10），Ksy=diag（0.00002，…，0.00002），KΦ1＝KΦ2＝I5×5，理想内应力fd1=fd2=0。模糊系统由5个使用高斯函数的模糊规则构成。

表1 相机参数Tab.1 Camera parameter

选定的2个特征点在末端执行器1和2坐标系下的坐标分别是（-0.03，0，0.06），（-0.03，0，0.18），（0.03，0，0.18），（0.03，0，0.06）。 特征点 1 在图像平面1和2上的理想轨迹的定义如表2所示。

表2 理想轨迹Tab.2 Disired trajectory

由于相机成像存在非线性，因此特征点2在图像平面1和2上的理想轨迹和很难直接定义给出，因此，仿真中和的值通过特征点1和2之间的相对位置关系计算得到。

从图2～图3可以看到2个特征点在图像平面1和2上都能很好的跟踪上理想的轨迹。图4～图5显示的是位置跟踪误差的变化情况，从图中可以详细的看到跟踪能够快速收敛，最后收敛到零。图6～图7显示的是双臂上内应力跟踪误差的情况，从图中可看出内应力也能很好地跟踪上理想值。从仿真结果可以证明本文提出的控制方法是有效的。

图2 相机1上的跟踪轨迹Fig.2 Tracking trajectory on camera 1

图3 相机2上的跟踪轨迹Fig.3 Tracking trajectory on camera 2

图4 相机1上的跟踪误差Fig.4 Tracking error on camera 1

图5 相机2上的跟踪误差Fig.5 Tracking error on camera 2

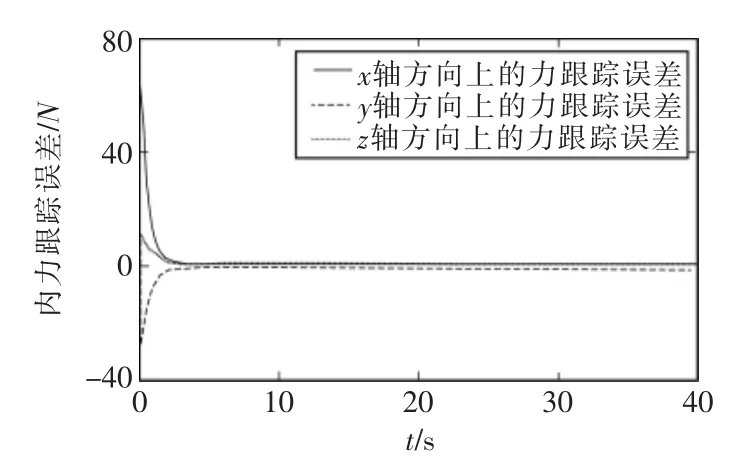
图6 左臂上内力跟踪误差Fig.6 Internal force tracking error on arm 1

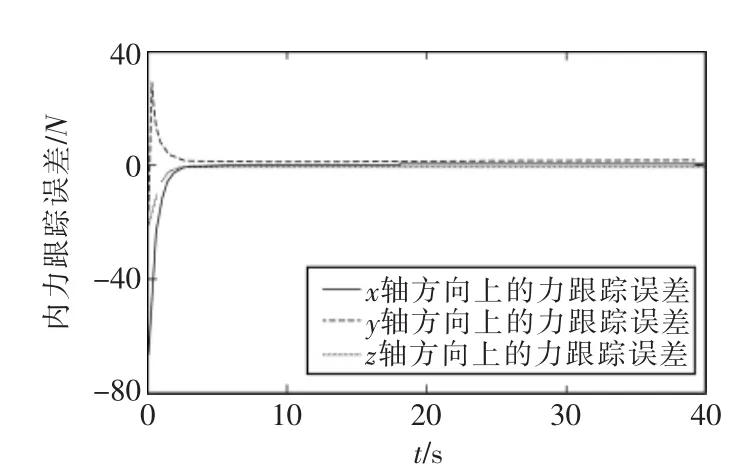
图7 右臂上内力跟踪误差Fig.7 Internal force tracking error on arm 2

6 结语

本文研究了双臂系统在双目视觉的监控下执行轨迹跟踪任务。首先，针对目标的动力学不确定性，在控制设计中引入模糊逻辑系统。接下来在位置/力混合控制框架下，设计了基于双目视觉的双臂模糊轨迹跟踪控制器，并且通过仿真验证了控制方法的有效性。

[1] W.Gueaieb，F.Karray，S.Al-Sharhan.A robust adaptive fuzzy position/force controlscheme forcooperative manipulators[J].Control Systems Technology，IEEE Transactions on，2003（4）：516-528.

[2] W.Gueaieb，F.Karray，S.Al-Sharhan.A robust hybrid intelligent position/force control scheme for cooperative manipulators[J].IEEE-ASME Transactions on Mechatronics，2007（12）：109-125.

[3] Z.Liu，C.Chen，Y.Zhang.Decentralized robust fuzzy adaptive control of humanoid robot manipulation with unknown input backlash：An experimental study[J].Fuzzy Systems，IEEE Transactions on，2015，23（3）：605-616.

[4] N.Kumar，V.Panwar，N.Sukavanam.Neural network control of coordinated multiple manipulator systems[C]//Computing：Theory and Applications，2007，International Conference on，2007：250-256.

[5] Z.Liu，C.Chen，Y.Zhang，et al.Adaptive neural control for dualarm coordination of humanoid robot with unknown nonlinearities in output mechanism[J].Cybernetics，IEEE Transactions on，2015，45（3）：521-532.

[6] K.K.Tan，S.Huang，T.H.Lee.Decentralized adaptive controller design of large-scale uncertain robotic systems[J].Automatica，2009，45（1）：161-166.

[7] Z.J.Yang，Y.Fukushima，P.Qin.Decentral ized adaptive robust control of robot manipulators using disturbance observers[J].IEEE Transactions on Control Systems Technology，2012，20（5）：1357-1365.

[8] M.Namvar，F.Aghili.Adaptive force-motion control of coordinated robots interacting with geometrically unknown environments[J].IEEE Transactions on Robotics，2005，21（4）：678-694.

[9] C.C.Cheah，S.P.Hou，Y.Zhao，J.-J.Slotine.adaptive vision and force tracking control for robots with constraint uncertainty[J].Mechatronics，IEEE/ASME Transactions on，2010，15 （3）：389-399.

[10]F.Nadi，V.Derhami，M.Rezaeian.Visual servoing control of robot manipulator with jacobian matrix estimation[C]//Robotics and Mechatronics 2014 Second RSI/ISM International Conference，2014：405-409.

[11]H.Wang.Adaptive visual tracking for robotic systems without image-space velocity measurement[J].Automatica，2015，55（C）：294-301.

[12]H.Wang，M.Jiang，W.Chen，Y.-H.Liu.Visual servoing of robots with uncalibrated robot and camera parameters[J].Mechatronics，2012，22（6）：661-668.

[13]K.Wang，Y.Liu，L.Li.Visual servoing trajectory tracking of nonholonomic mobile robots without direct position measurement[J].Robotics，IEEE Transactions on，2014，30（4）：1026-1035.

[14]J.Qu，F.Zhang，Y.L.Fu，etal.Approach movementofredundant manipulator using stereo vision[C]//Robotics and Biomimetics，2014 IEEE International Conference，2014：2489-2494.

[15]Y.Wang，G.lu Zhang，H.Lang，et al.A modified image-based visual servo controller with hybrid camera configuration for robust robotic grasping[J].Robotics and Autonomous Systems，2014，62（10）：1398-1407.

[16]H.Wang，Y.-H.Liu，D.Zhou.Dynamic visual tracking for manipulators using an uncalibrated fixed camera[J].Robotics，IEEE Transactions on，2007，23（3）：610-617.

Binocular Vision Based on Fuzzy Trajectory Tracking Control for Dual-arm System

WANG Yong1，2，LIU Zhi1
（1.Faculty of Automation，Guangdong University of Technology，Guangzhou 510006，China；2.The center of education technology，Guangdong University of Foreign Studies，Guangzhou 510420，China）

The object held by a dual-arm system is to perform a visual trajectory tracking task in the monitoring of a binocular vision system.The control performance should be degraded by the dynamics uncertainties generated from the random holding manner，especially when the object with large mass.As a result，the fuzzy system is then introduced to approximate the dynamics characteristic.At the same time，the decentralized control method is used to address the cooperation between the dual arms，and the binocular vision based fuzzy trajectory tracking controller for dual-arm system is designed based on position/force hybrid control framework.Finally，the effectiveness of the proposed controller is verified in simulation.

dual-arm system；binocular vision servoing；position/force hybrid control

TP273

A

1001-9944（2017）11-0010-05

10.19557/j.cnki.1001-9944.2017.11.003

2017-04-19；

2017-07-24

国家自然科学基金项目（61573108）

王勇（1977—），男，博士，研究方向为视觉伺服，自适应控制；刘治（1977—），男，教授，博士生导师，研究方向为非线性控制、机器人控制。