电网大扰动动态稳定影响因素分析

曹生顺，张文朝，范新桥，孟杰，李少岩

（1.国家电网公司西北分部，陕西西安 710048；2.南京南瑞集团公司，江苏南京 210003；3.北京信息科技大学自动化学院，北京 100192；4.国网河北省电力公司河北电力科学研究院，河北石家庄050021；5.华北电力大学电气与电子工程学院，河北保定 071003）

随着我国电网规模的日益扩大、大区电网互联，电力系统动态稳定性问题越来越突出[1-4]。动态稳定是指电网受到扰动后，在自动调节和控制装置的作用下，保持较长过程运行稳定性的能力。根据扰动的大小，动态稳定可分为小扰动动态稳定和大扰动动态稳定。

近年来，关于小扰动动态稳定已有相对成熟的理论与研究方法，包括负阻尼、强迫振荡等理论[5-10]，研究方法有特征值分析、时域仿真等方法[11-12]。通常利用PSD-SSAP、PSASP的小干扰分析软件和基于时域仿真的电力系统仿真软件对其进行分析，采用的一般都是特征值分析方法。电力系统的阻尼特性主要受调速系统、励磁系统、PSS装置、负荷以及线路阻抗等因素的影响。文献[13]研究了负荷模型特性对电网动态稳定的影响；文献[14]从数学上推导了励磁系统对电网动态稳定的影响；文献[15]研究了调速系统对电网阻尼特性的影响；文献[16]得出重要断面输送潮流变化对振荡模式的阻尼比有很大影响的结论。当前关于大扰动动态稳定的相关研究主要局限于简单小系统，且未见工程应用。文献[17]运用向量场正则形理论，得到了简单电力系统状态方程的2阶解析解和鉴别大干扰下主导低频振荡模式的方法，文献[18]提出了由于电力系统3阶解析解中非线性高阶项被大干扰激发，使系统模态间的高阶非线性相互作用加剧，从而导致系统出现增幅低频振荡的观点等等。

当电网受到大功率缺额、关键线路断开等大扰动时，电网某些振荡模式的阻尼特性恶化，则会影响到电网的正常运行，严重时可能造成电网失稳。因此，研究电网大扰动动态稳定性对保证电网安全运行具有重要意义。电网受到大扰动后，先后经历过渡期与平稳期。当电网处于过渡期，电网自动调节和控制装置可能处于限幅状态，从而影响电网阻尼特性；当电网进入平稳期时，电网运行于事故后方式，自动调节和控制装置趋于稳定状态，线路潮流重新分配，网架结构发生改变，系统阻尼特性也随之改变。

综上所述，实际电网受到大扰动后，其阻尼特性可能主要取决于电网中的非线性因素和事故后运行方式。因此，本文从这两方面因素出发，研究其对电网大扰动后动态稳定性的影响，并通过实际电网的仿真分析对所提结论进行了验证。

1 事故后方式对电网大扰动动态稳定的影响

当电网受到大扰动后，线路潮流会重新分配，由于电网网架结构和电网运行方式发生改变，使得电网自身的阻尼特性也发生相应变化。

为验证事故后运行方式对电网大扰动动态稳定的影响，采用PSD-BPA搭建了如图1所示的单机无穷大系统。系统基准容量为100 WM，发电机G1的额定容量S1为1 000 MW，出力为700 MW，电抗标幺值XG为0.03，线路电抗标幺值XL为0.07。用SSAP软件对系统进行小干扰分析，分析结果振荡频率为0.872 7 Hz、阻尼比为0.092 0。

图1 单机无穷大系统Fig.1 Single-machine infinite bus system

设置断线大扰动故障，进行大扰动时域仿真。以发电机G1为参考机。发电机G1的速度偏差、励磁电压、调压器输出信号、PSS输出信号等输出曲线均未到达限幅值。通过Prony算法计算得出低频振荡主导模式的振荡频率为0.587 8 Hz、阻尼比为0.056 4。

事故后，由于单机无穷大系统的拓扑结构发生改变，导致电网振荡频率由0.872 7 Hz变为0.587 8 Hz，同时阻尼比由0.092 0变为0.056 4，阻尼特性变差。

进一步对事故后方式进行时域仿真，得到事故后系统平稳运行时发电机G1的有功功率、无功功率，根据事故后电网的拓扑结构，从而得到电网的事故后方式。使用SSAP软件对事故后方式进行小干扰动态稳定分析，分析结果振荡频率为0.602、阻尼比为0.054。

与时域仿真的计算结果进行对比，事故后方式下电网自身的阻尼特性与大扰动后时域仿真结果接近。大扰动过程中，PSS装置、调速系统等自动调节装置均未越限，因此可认为在自动装置未达到限幅时，大扰动后的动态稳定性与事故后方式小干扰阻尼特性所决定。

2 非线性因素对电网大扰动动态稳定的影响

由于电力系统中存在大量非线性的自动调节和控制装置，当电力系统遭受大扰动时，电网自动调节和控制装置处于限幅状态，电力系统低频振荡模式的阻尼特性随之发生改变，从而影响电网的动态稳定性。文献[15]指出当电网受到扰动后，原动机调节系统的死区、纯延时、限幅等非线性环节通过改变机械转矩影响转子运动，从而影响电力系统动态稳定。

励磁系统非线性主要体现在故障期间的强励，调速系统的非线性主要体现在限幅环节，励磁系统强励主要体现在快速的暂态过程中，而调速系统响应时间相对较慢，两者对故障后动态摇摆过程影响相对较小。而PSS装置与电网阻尼特性关系最为密切，本节主要讨论PSS装置限幅环节对电网阻尼特性的影响。

仿真系统中PSS模型的最大输出VSMAX和最小输出VSMIN分别设置为±0.1、±0.07、±0.05，通过在线路1上加瞬时性短路故障设置大扰动故障。时域仿真中PSS输出曲线和线路有功功率分别如图2和图3所示。

根据表1不同限幅作用下电网振荡模式阻尼特性计算结果可知，随着限幅幅值的不断减小，限幅作用不断增大，振荡模式的阻尼比不断减小。

将PSS模型的最大输出VSMAX和最小输出VSMIN分别设置为±0.05，其中一回线路上加瞬时性短路故障，短路持续时间分别设为0.25 s、0.1 s、0.05 s。时域仿真中PSS输出曲线和线路有功功率曲线分别如图4和图5所示。

从图4与表2可与看出，随着扰动的不断增大，PSS输出信号进入限幅的时间不断增长，振荡模式的阻尼比不断减小。

根据仿真结果，限幅幅值与扰动大小对PSS的输出信号影响较大，PSS装置的限幅值越小、限幅时间越长，PSS装置所产生的阻尼力矩越小，而电网的阻尼特性则越差；由于设置故障为瞬时故障，系统事故后运行方式不变，所以可认为大扰动后电网动态稳定性主要由PSS装置的非线性环节决定。

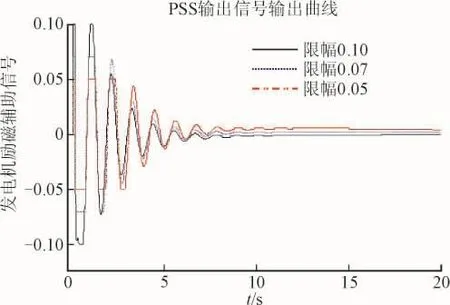
图2 不同限幅作用下发电机PSS输出曲线Fig.2 PSS output curves of the generator under different limiting actions

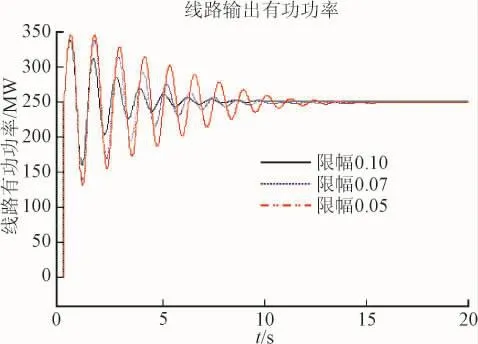
图3 不同限幅作用下线路有功功率曲线Fig.3 Line active power curves under different limiting actions

图4 不同扰动下发电机PSS输出曲线Fig.4 PSS output curves of the generator under different disturbances

图5 不同扰动下线路有功功率曲线Fig.5 Line active power curves under different disturbances

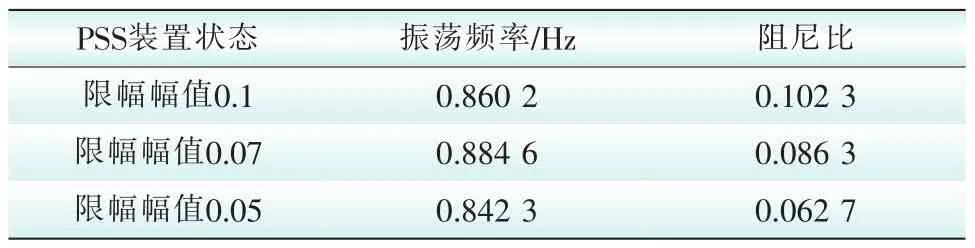
表1 不同限幅作用下电网振荡模式阻尼特性Tab.1 Power grid oscillation mode damping characteristics under different limiting actions

表2 不同扰动下电网振荡模式阻尼特性Tab.2 Power grid oscillation mode damping characteristics under different disturbances

3 两因素共同作用的大扰动动态稳定分析

由于直接准确求取事故后运行方式较为繁琐和困难，而通过观测速度偏差、励磁电压、PSS输出信号等参数的输出曲线是否在限幅之内则相对简单。因此，如果电网速度偏差、PSS输出信号等参数的时域仿真曲线大都在限幅之内，且处于限幅状态的装置退出运行，则其对电网阻尼特性影响不大，那么就可以认为电网大扰动动态稳定特性主要由事故后方式下电网自身的阻尼特性所决定。

采用前述单机无穷大系统。设置断线大扰动故障，逐渐减小单机无穷大系统PSS装置的限制幅值，观测对比电网受到大扰动时的阻尼特性与事故后运行方式下电网自身的阻尼特性。时域仿真PSS信号输出曲线和线路有功功率分别如图6和图7所示。

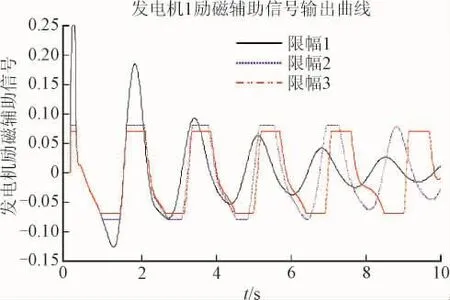
图6 发电机PSS输出信号输出曲线Fig.6 PSS output curves of the generator

图7 线路有功功率曲线Fig.7 Line active power curves

将PSS模型的最大输出VSMAX和最小输出VSMIN分别设置为±0.25（PSS输出信号不受限制）、±0.08、±0.07（电网大扰动动态稳定突变）三个档位。分别记这3个档位为限幅1、限幅2、限幅3。根据仿真结果可计算出表3所示的阻尼特性。

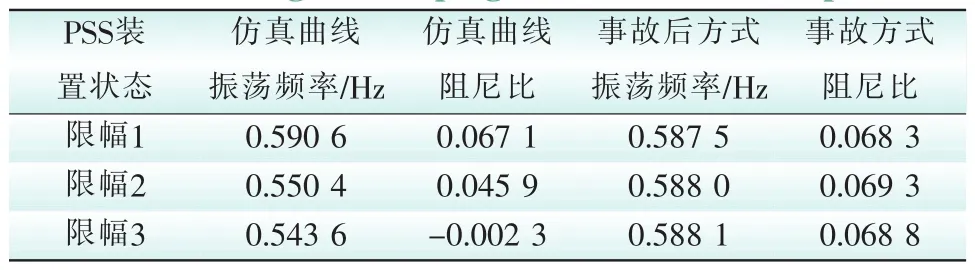
表3 电网阻尼特性对比Tab.3 Power grid damping characteristics comparison

由表3的计算结果可知，随着限幅作用的减弱，时域仿真曲线的阻尼比与事故后方式的阻尼比越来越接近。因此，如果电网在大扰动动态过程中，速度偏差、PSS信号等输出曲线大都在限幅之内，则电网大扰动动态稳定特性由事故后方式下电网自身的阻尼特性所决定。

4 算例分析

4.1 电网大扰动故障时域仿真算例

运用小干扰软件（SSAP）对某实际电网2017年夏季平峰方式进行低频振荡计算，经分析可得该电网MX地区对SD地区振荡模式的振荡频率为0.404 4 Hz，阻尼比为0.053 6。

采用BPA潮流、稳定计算程序对电网大功率缺额故障进行时域仿真。运用Prony算法计算MX地区四回外送联络线有功功率曲线的阻尼比，计算结果如表4所示。

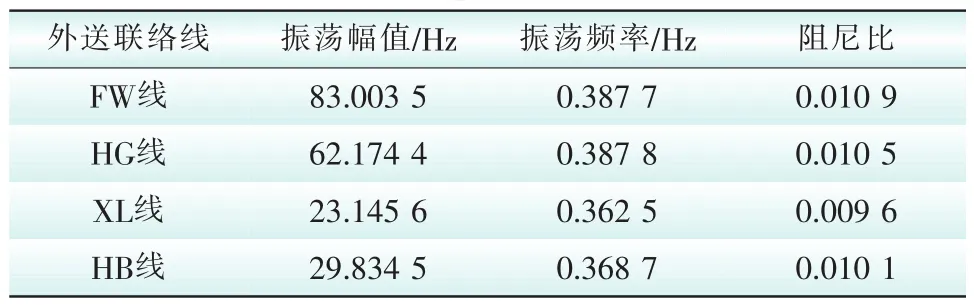
表4 MX地区外送联络线prony计算结果Tab.4 Calculation results of MX Area outgoing lines by using the prony method

小干扰特征值计算结果反映的是事故前MX地区对SD地区振荡模式的阻尼特性，时域仿真结果反映的是事故后MX地区对SD地区振荡模式的阻尼特性。由表4计算结果可知，事故后MX地区对SD地区振荡模式的阻尼比由0.053 6变为0.010 3，阻尼特性变差。

当电网出现大功率缺额时，整个电网的发电机组受到大的扰动，发电机的调速系统、励磁装置、PSS装置的输入信号处于持续振荡中，一部分自动控制装置可能进入限幅区域，从而影响电网的动态稳定性。进行大扰动时域仿真可得所有机组的速度偏差、励磁电压、机械功率、PSS输出等曲线，根据表5所示的统计结果可知，只有少数PSS输出进入限幅区域。

表5 PSS输出信号进入限幅区域的发电机组统计Tab.5 Generators with its PSS output signal in clipping region

进一步，将进入限幅区域的发电机组PSS全部退出，观测MX地区-SD地区主导振荡模式的频率、阻尼比等参数的变化规律。

根据表6对比结果，该方式下PSS退出后MX地区-SD地区振荡模式的阻尼比变化较小。

表6 进入限幅区域的PSS灵敏度分析Tab.6 Sensitivity analysis of PSS going into clipping region

由于发生大扰动而进入限幅区域的机组数目较少，且对MX地区-SD地区振荡模式的阻尼比影响不大。因此可认为该电网的大扰动动态稳定特性主要由事故后电网自身的阻尼特性决定。

4.2 电网事故后方式阻尼特性分析验证算例

对同一电网2017年夏季平峰、大功率缺额故障进行时域仿真，输出该电网所有发电机的电磁功率曲线。根据电磁功率曲线得到事故后各发电机的稳态出力，将稳态出力数据作为潮流文件中发电机实际出力，即为事故后方式。

事故后方式下，主要联络线的潮流与对应的时域仿真输出联络线潮流结果如表7所示。

表7 联络线潮流对比Tab.7 Power flow comparison of connection lines

采用SSAP软件对事故后方式进行小干扰分析，可得MX地区对SD地区振荡模式的振荡频率为0.383 Hz，阻尼比为0.011 6。与表4结果进行对比可知，事故后方式下MX地区对SD地区振荡模式的阻尼比与时域仿真得到的结果更相近。因此，该电网的大扰动动态稳定特性主要由事故后电网自身的阻尼特性决定的结论得到验证。

5 结论

电力系统受到大扰动后，由于动态过程中非线性因素和事故后运行方式改变两方面因素，电网阻尼特性发生改变。本文通过对该两方面因素进行仿真分析，得出电网受到大扰动后，如果自动调节控制装置的非线性环节对电网阻尼特性影响较小，则电网大扰动动态稳定性主要由事故后方式下电网自身阻尼特性所决定。最后，通过对某实际电网进行大扰动故障和事故后方式仿真，验证了所得结论的准确性，结果也表明可采用小扰动法分析事故后大扰动下电网的稳定性。本文所得结论可为工程上研究电网大扰动动态稳定性提供一种新思路。

[1]朱方，赵红光，刘增煌，等.大区电网互联对电力系统动态稳定性的影响[J].中国电机工程学报，2007，27（1）：1-7.ZHU Fang，ZHAO Hongguang，LIU Zenghuang，et al.The influence of large power grid interconnected on power system dynamic stability[J].Proceedings of the CSEE，2007，27（1）：1-7 （in Chinese）.

[2]朱方，汤涌，张东霞，等.我国交流互联电网动态稳定性的研究及解决策略[J].电网技术，2004，28（15）：1-5.ZHU Fang，TANG Yong，ZHANG Dongxia，et al.Study ondynamicstabilityproblemsofACinterconnectedareapower grids in china and their solutions[J].Power System Technology，2004，28（15）：1-5（in Chinese）.

[3]梁艳红，张文朝，李付强，等.链式电网动态稳定下多断面耦合特性研究[J].电力系统保护与控制，2017，45（4）：107-113.LIANG Yanhong，ZHANG Wenchao，LI Fuqiang，et al.Research on multi-sections coupling characteristics of chain network dynamic stability[J].Power System Protection and Control，2017，45（4）：107-113（in Chinese）.

[4]丁建顺，王青，马世英，等.发电机叠加型低励限制对电力系统动态稳定影响机制[J].电力系统自动化，2016，40（8）：78-84，91.DING Jianshun，WANG Qing，MA Shiying，et al.Influence mechanism of superimposed type of underexcitation limiter in generators on power system dynamic stability[J].Automation of Electric Power System，2016，40（8）：78-84，91（in Chinese）.

[5]刘巨，汪锦，姚伟，等.负阻尼和强迫功率振荡的特征分析与区分方法[J].电力系统保护与控制，2016，44（19）：76-84.LIU Ju，WANG Jin，YAO Wei，et al.Characteristic analysis and identification method of negativedamping and forced power oscillation[J].Power System Protection and Control，2016，44（19）：76-84（in Chinese）.

[6]DOBSON I，ZHANG Jianfeng，GREENE S，et al.Is strong modal resonance a precursor to power system oscillations[J].IEEE Transactions on Circuits and Systems-I：Fundamental Theory and Applications，2001，48（3）：340-349.

[7]GOMES S Jr.MARTINS N，PORTELA C.Computing smallsignal stability boundaries for large-scale power systems[J].IEEE Transactions on Power Systems，2003，18（2）：747-752.

[8]王佳明，刘文颖，牛拴保.新疆-西北电网联网前后阻尼特性研究[J].电力系统保护与控制，2010，38（16）：92-98.WANG Jiaming，LIU Wenying，NIU Shuanbao.Study on damping characteristics of xinjiang-northwest power grid before and after interconneetion[J].Power System Protection and Control，2010，38（16）：92-98（in Chinese）.

[9]汤涌.电力系统强迫功率振荡的基础理论[J].电网技术，2006，30（10）：29-33.TANG Yong.Fundamental theory of forced power oscillation in power system[J].Power System Technology，2006，30（10）：29-33（in Chinese）.

[10]徐衍会，贺仁睦，韩志勇.电力系统共振机理低频振荡扰动源分析[J].中国电机工程学报，2007，27（17）：83-87.XU Yanhui，HE Renmu，HAN Zhiyong.The cause analysis of turbine power disturbance inducing power system low frequency oscillation of resonance mechanism[J].Proceedings of the CSEE，2007，27（17）：83-87（in Chinese）.

[11]杜正春，刘伟，方万良，等.小干扰稳定性分析中一种关键特征值计算的稀疏实现[J].中国电机工程学报，2005，25（2）：17-21.DU Zhengchun，LIU Wei，FANG Wanliang，et al.A sparse method for the calculation of critical elgenvalue in small signal stability analysis[J].Proceedings of the CSEE，2005，25（2）：17-21（in Chinese）.

[12]潘学萍，薛禹胜，张晓明，等.轨迹特征根的解析估算及其误差分析[J].电力系统自动化，2008，32（19）：10-14.PAN Xueping，XUE Yusheng，ZHANG Xiaoming，et al.Analytical calculation of power system trajectory eigenvalues and its error analysis[J].Automation of Electric Power System，2008，32（19）：10-14（in Chinese）.

[13]邹德旭，贺仁睦，司大军.负荷模型对电力系统动态稳定的影响[J].电力系统及其自动化，2011，23（1）：118-122.ZOU Dexu，HE Renmu，SI Dajun.Effects of load model on dynamic stability in power system[J].Automation of Electric Power System，2011，23（1）：118-122（in Chinese）.

[14]石雪梅，汪志宏，桂国亮，等.发电机励磁系统数学模型及参数对电网动态稳定性分析结果影响的研究[J].继电器，2007，35（21）：22-27.SHI Xuemei，WANG Zhihong，GUI Guoliang，et al.Research on the influence of generators based on detailed excitation system models and parameters to power grid dynamic stability[J].Relay，2007，35（21）：22-27（in Chinese）.

[15]王官宏，陶向宇，李文峰，等.原动机调节系统对电力系统动态稳定的影响[J].中国电机工程学报，2008，28（34）：80-86.WANG Guanhong，TAO Xiangyu，LI Wenfeng，et al.Influence of turbine governor on power system dynamic stability[J].Proceedings of the CSEE，2008，28（34）：80-86（in Chinese）.

[16]刘学智，刘涤尘，袁荣湘，等.联络线潮流对互联电网低频振荡模式的影响[J].中国电力，2009，42（10）：39-41.LIU Xuezhi，LIU Dichen，YUAN Rongxiang，et al.The influence of tie-line power flow on low-frequency mode in interconnected power system[J].Electric Power，2009，42（10）：39-41（in Chinese）.

[17]邓集祥，华瑶，韩雪飞.大干扰稳定中低频振荡模式的作用研究[J].中国电机工程学报，2003，23（11）：60-64.DENG Jixiang，HUA Yao，HAN Xuefei.Study on effect of low frequency oscillation modes in large disturbance stability[J].Proceedings of the CSEE，2003，23（11）：60-64（in Chinese）.

[18]邓集祥，陈武晖，贺建明.应用模态级数3阶解析解分析大干扰低频振荡机理[J].电力系统及其自动化，2007，31（22）：27-30.DENG Jiaxiang，CHEN Wuhui，HE Jianming.Mechanism analysis of increasing amplitude low frequency oscillation based on modal series with third-order analytical solution[J].Automation of Electric Power System，2007，31（22）：27-30（in Chinese）.