基于改进量子遗传算法的配电网无功优化研究及应用

向萌，左剑，王文林，余东真，谢晓骞

（1.国网湖南省电力公司电力科学研究院，湖南长沙 410007；2.国网安徽省电力公司黄山供电公司，安徽黄山 245000；3.华北电力大学，北京 102206；4.国网湖南省电力公司，湖南长沙 410007）

电力系统的运行管理不仅要重视安全可靠性，还要充分考虑运行的经济性。研究电力系统无功优化的目的，就是要通过调整无功潮流的科学合理分布来保证无功功率的平衡，有效降低网损，在保障电力系统安全稳定运行的同时提高经济效益。作为电力系统能量损耗的主体部分，配电网是电力系统无功优化的研究重点。配电网无功优化问题是一个多变量、多约束的混合非线性规划问题，其控制既有连续变量又有离散变量，整个优化过程十分复杂。20世纪60年代初，文献[1]首先提出了电力系统最优潮流（optimal power flow，OPF）的概念与模型[1]，由此电力系统潮流优化问题在理论研究和实际应用上都有了很大发展。几十年来，国内外专家学者在进行了大量的研究工作后[2]，提出了许多算法及改进算法，归纳起来可以分为2大类[3]：一是经典的无功优化算法[4-6]，如解析法、线性规划等。这些算法对数学模型的要求高，难以同时满足算法的精确性与实时性。二是基于人工智能的无功优化算法，如遗传算法[7-8]、蚁群算法[9]、模拟退火算法[10]、混沌算法[11-12]等，其中最典型的为遗传算法（GA），其特点是不依赖于梯度信息，通过模拟生物进化过程来寻找最优解。虽然它能较好地处理离散变量，具有很强的鲁棒性和广泛的适用性，但由于GA通过选择、交叉、变异操作来更新种群，很难同时实现种群多样性和选择压力的特性，存在迭代次数多、搜索速度慢、易陷入局部极值和过早收敛等不足[13-15]。

为此，本文提出一种基于改进量子遗传算法的配电网无功优化方法。量子遗传算法（quantuminspired genetic algorithm，QGA）是由Han[16]等提出，以量子计算理论[17]为基础的概率搜索算法。本文的改进量子遗传算法（improved quantum-inspired genetic algorithm，IQGA）以QGA为基础，采用量子比特概率幅对控制变量进行编码，提高了算法的计算效率，丰富了种群多样性；提出新的量子交叉与变异方式，避免了个体收敛于自身的局部最优解。

1 配电网无功优化数学模型

本文综合考虑有功网损最小、配电网电能质量指标及配电网实际情况，采用的目标函数为满足电压不越限的条件下求解有功网损最小值，其中电压越限作为罚函数出现在目标函数中。选取节点电压Vi为状态变量，可调变压器分接头档位Tj、无功补偿电容投切组数Qck和线路的无功补偿点K为控制变量。

目标函数为

其中Viset取值为

功率约束方程为

状态变量约束条件[18]为

控制变量约束条件为

式中：Ploss为网损；γv为电压越限惩罚因子；Pi，Qi分别为节点i的注入有功功率和无功功率；θij为Vi与Vj之间的相角差；Gij和Bij分别为节点i和节点j之间的电导与电纳；n为节点数；j∈i表示所有与节点i相连的节点；Vi为节点电压；Viset为节点设定电压；Vimax，Vimin分别为节点电压的上、下限。Tjmax，Tjmin为可调变压器分接头档位的上、下限；Qckmax，Qckmin为补偿电容投切组数的上、下限；j为变压器支路数；K为无功补偿点；Qcsite为线路上可加的无功补偿点。

2 基于IQGA的无功优化方法

为更好地解决无功优化问题，IQGA结合量子计算的概念和理论，采用量子比特概率幅编码，构建模型个体，并提出新的量子交叉与变异方法，将其他个体的目标值作为本个体的目标进行更新，缩短了运算周期，提高了算法的计算效率与全局寻优能力。基于IQGA的电力系统无功优化流程如下：

1）取线路、负荷节点等的原始数据输入系统，构造由系统控制变量组成的个体，随机产生初始种群。

4）对R（t）中的每个个体进行适应度评价并采用牛顿-拉夫逊潮流计算方法求解潮流方程，得到所有状态变量的值，包括各个节点的电压和相角。

5）以配电网有功损耗作为优化过程中的适应度函数，计算得到适应度函数值，将适应度函数值作为适应值。记录种群的最优个体Xqgbest及其适应值、每个个体进化过程中局部最优个体Xqpbestj及其适应值。

6）判断是否满足终止进化准则，若达到结束条件则中止，转步骤7），如果不满足则转步骤8）继续。

7）输出优化结果，包括各控制变量、状态变量的值、系统潮流水平以及系统有功损耗等，结束。

8）以轮盘赌的方式抽取个体进行量子交叉。

9）对量子个体进行量子变异，产生新种群，令t=t+1，进入步骤3）。

改进量子遗传算法无功优化的流程图如图1所示。

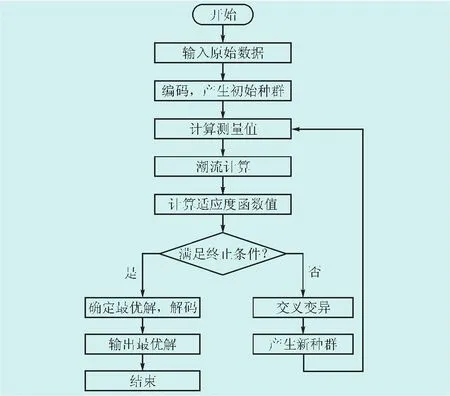
图1 IQGA无功优化流程图Fig.1 The flow chart of the reactive power optimization based on IQGA

2.1 编码

步骤1）中的量子编码[19]采用概率幅编码方式，在编码矩阵中每一个二进制码都采用量子位表示：

式中：α，β代表相应状态出现概率幅值的2个复数。|α|2和|β|2分别表示量子比特处于状态“0”和状态“1”的概率，满足|α|2+|β|2=1。此时|α|2或|β|2使得量子位能分别表示“0”状态或“1”状态。每个长度为m个量子位的q染色体如下：

一个量子个体是由m个量子位的概率幅值组成的串，定义为

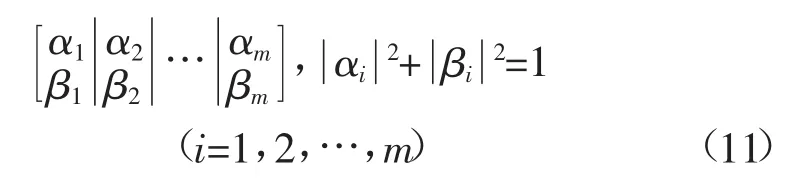
可以看出，一个具有m个量子位的量子个体，它可以表示2m个状态。例如，假设1个量子个体，由2个量子位组成，它的2对幅值为那么它的状态则可以表示为换而言之，它表示量子位处于状态状态|00〉，|01〉，|10〉，|11〉的概率分别为1/8，1/8，3/8和3/8。因此，1个2个量子位的量子个体，可以表示4种状态，这样种群的多样性得到丰富，更利于算法在搜索空间探索。

按此方法各控制变量可表示为

Uq=，用k个量子比特表示发电机机端电压（k取决于实数精度）。

Tq=，用l个量子比特表示有载可调变压器变比分接头档位（l取决于接头调控范围）。

Nq=，用m个量子比特表示无功补偿装置投切组数（m取决于投切组数调控范围）。

由此一个完整的染色体可以表示为Xq=[UqTqNq]。

2.2 交叉与变异

在步骤8）的量子交叉中，通过轮盘赌方式挑选出个体XqA和XqB，以个体XqA的局部最优目标XqpbestA作为个体XqB的局部最优目标，对个体XqB进行一次量子旋转门的更新。以个体XqB的局部最优目标XqpbestB作为个体XqA的局部最优目标，对个体XqA进行一次量子旋转门的更新。还原各自的局部最优目标，从而产生新种群。

步骤9）的量子变异操作：当随机概率小于变异概率时，对量子个体进行变异，变异操作即互换量子个体的α和β值，重新生成新的个体。

3 某城区局部中压配电网实例分析

利用某城区局部中压配电网线路作为算例进行计算分析。使用ETAP软件对该线路进行潮流计算，得到潮流分析结果如图2所示，据此简化整理得到39节点的电路（支路38条，节点1为平衡节点，其余为PQ节点）。根据变压站设备参数（基准功率为10MV·A，基准电压为10 kV，机端电压设为1.05 pu），将节点数据转化成标幺值进行计算。控制变量及状态变量约束如表1所示，其中变压器变比与无功补偿容量为控制变量，负荷节点电压为状态变量，表1中数据均为标幺值。当系统运行在初始状态，即未采用优化手段时，线路初始有功网损为26.71 kW。依据实际调研结果，设定在线路上的无功补偿点不超过2个，每个点的总补偿量设为10组补偿，单组为50 kV·A。

分别采用本方法、遗传算法（geneticalgorithm，GA）和量子进化算法（quantum-inspired evolutionary algorithm，QEA）求最优解，均迭代10次，进化代数设为100，种群数设为20。运行得到的收敛曲线分别如图3—图5所示，将3种算法的优化结果输出比较，比较结果见表2。

表1 状态变量及控制变量约束条件统计表Tab.1 The statistics of the state variable and control variables’constraint condition pu

表2 不同算法优化比较结果统计表Tab.2 The statistic of optimization comparison results by different methods

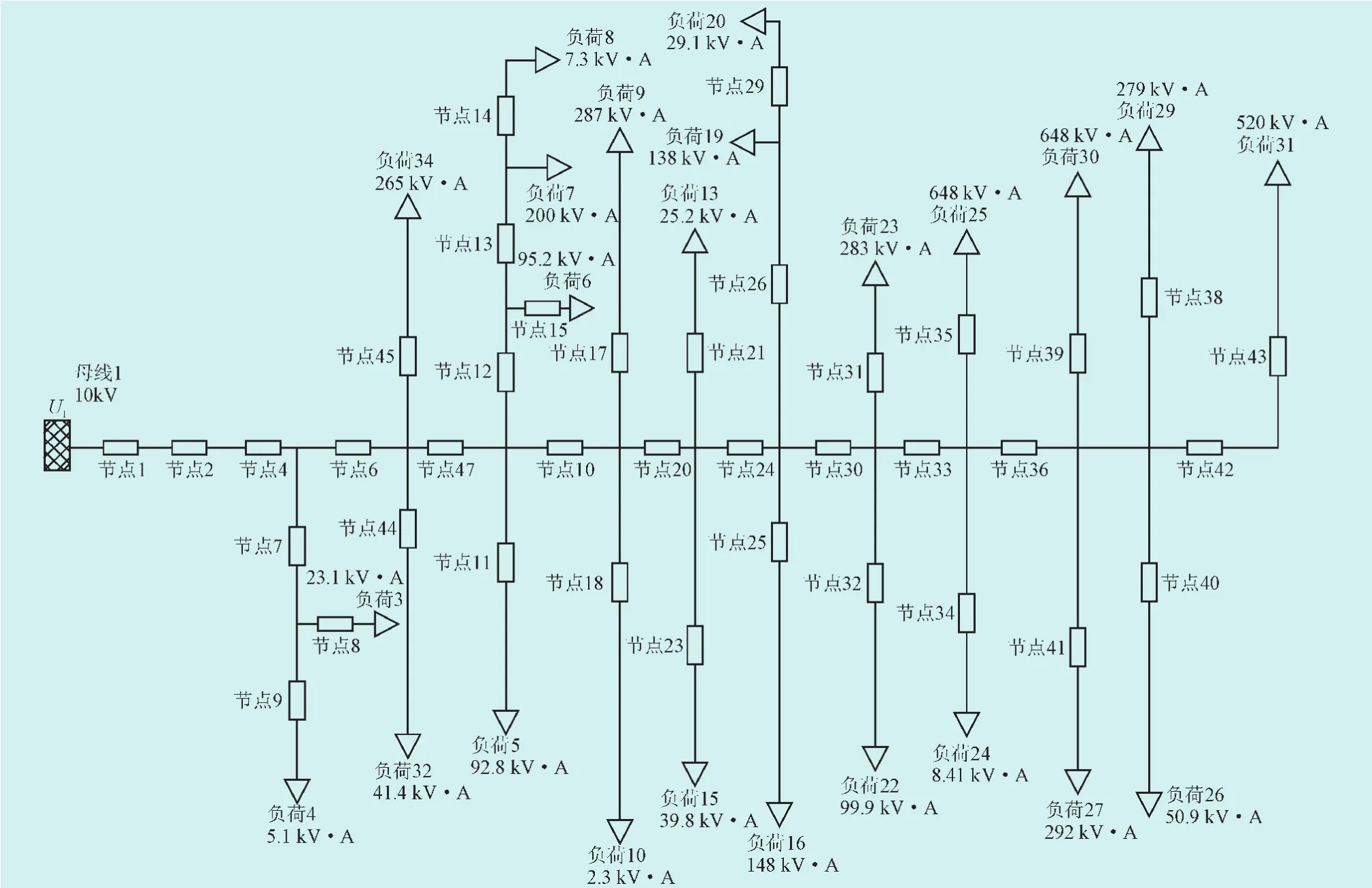
图2 潮流分析结果Fig.2 The result of load flow analysis

由表2可知，3种算法得到的优化方案均能降低有功网损，采用GA、QEA优化得到的有功网损最优值分别为25.426 1 kW和25.440 1 kW，与初始值相比分别减少4.807%和4.754%，采用本文优化方法得到的有功网损最优值为25.419 2 kW，比初始值减少了4.833%，在3种算法中优化效果最佳。根据表2的对比结果可知，IQGA的全局寻优能力最好。由图3可知，采用IQGA进行无功优化时，在第52次迭代时找到了最优解，与GA（图4）和QEA（图5）相比，在避免了过早收敛于局部最优解的同时也提高了计算效率。

4 结论

针对优化过程复杂的配电网无功优化问题，本文以量子计算的概念和理论为基础，提出一种基于改进量子遗传算法的配电网无功优化方法，并采用某城区局部中压配电网线路作为算例进行计算分析，验证了该方法的有效性和优越性。

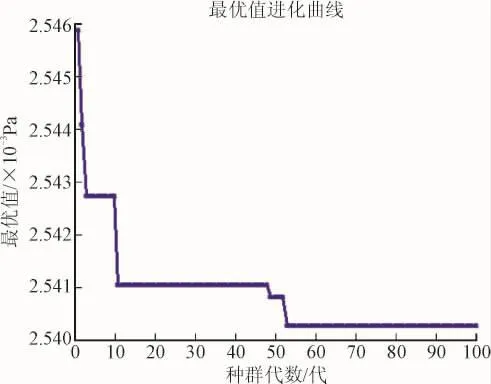
图3 基于IQGA的收敛曲线Fig.3 The optimization procedure based on IQGA

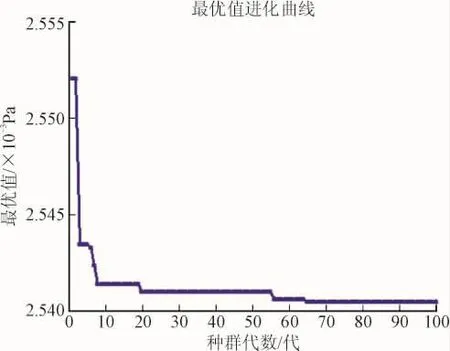
图4 基于GA的收敛曲线Fig.4 The optimization procedure based on GA

图5 基于QEA的收敛曲线Fig.5 The optimization procedure based on QEA

1）本文提出的改进的量子遗传算法采用量子比特概率幅编码，丰富了种群多样性，提高了计算效率。

2）算法中采用交换个体局部最优目标值的量子交叉方式和互换量子个体α和β值的量子变异方式，避免了个体收敛于自身局部最优解的情况，提高了算法的全局寻优能力。

3）考虑将该改进算法进一步产品化，建立现场的无功优化补偿系统，实现线路无功补偿优化配置，有助于推进配电网线路节能降耗，保障配电网安全经济运行。

[1]CARPENTIER J.Optimal power flows[J].International Journal of Electrical Power&Energy Systems，1979，1（1）：3-15.

[2]谢海波，武小梅，林翔，等.含分布式电源的配电网无功优化研究综述[J].广东电力，2017，30（2）:102-109.XIE Haibo，WU Xiaonei，LIN Xiang，et al.Review on reactive power optimization for power distribution network with distributed generation[J].Guangdong Power Journal 2017，30（2）:102-109（in Chinese）.

[3]周文俊，吴熙，施伟成.电力系统无功优化算法性能比较及分析[J].江苏电机工程，2013，32（4）:24-27.ZHOU Wenjun，WU Xi，SHI Weicheng.Comparison and analysis of algorithms for power system reactive power optimization[J].Jiangsu Electrical Engineering，2013，32（4）:24-27（in Chinese）.

[4]袁辉，徐贵光，周京阳.基于模糊线性规划的无功电压优化[J].电网技术，2003，27（12）：42-45.YUAN Hui，XU Guiguang，ZHOU Jingyang.A reactive power/voltage optimization based on fuzzy linear programming[J].Power System Technology，2003，27（12）：42-45（in Chinese）.

[5]胡晓阳，王卫平，王主丁，等.一种实用的配电网无功运行两层优化方法研究 [J/OL].电力系统保护与控制，2015，43（3）:14-21.HU Xiaoyang，WANG Weiping，WANG Zhuding，et al.A practical two-phase optimization method of dynamic var optimization in a distribution system[J].Power System Protection and Control，2015，43（3）:14-21（in Chinese）.

[6]吴丽珍，蒋力波，郝晓弘.基于最优场景生成算法的主动配电网无功优化 [J].电力系统保护与控制，2017，45（15）:152-159.WU Lizhen，JIANG Libo，HAO Xiaohong.Reactive power optimization of active distribution network based on optimal scenario generation algorithm[J].Power System Protection and Control，2017，45（15）:152-159（in Chinese）.

[7]马晋弢，LAI L L，杨以涵.遗传算法在电力系统无功优化中的应用[J].中国电机工程学报，1995，15（5）：347-353.MA Jintao，LAI L L，YANG Yihan.Application of genetic algorithm in reactive power optimization[J].Proceedings of the CSEE，1995，15（5）：347-353（in Chinese）.

[8]马立新，栾健.三目标遗传粒子算法的电力系统无功优化[J].华北电力大学学报（自然科学版），2015，42（3）:31-35.MA Lixin，LUAN Jian.Three-objective hybrid algorithm of genetic and particle swarm optimization for reactive power optimization[J].Journal of North China Electric Power University（Nature Science Edition），2015，42（3）：31-35（in Chinese）.

[9]李渊博，蒋铁铮.采用改进遗传算法的无功优化规划[J].电力科学与工程，2014，30（9）:39-45.LI Yuanbo，JIANG Tiezheng.Optimization of reactive power planning using improved genetic algorithm[J].Electric Power Science and Engineering，2014，30（9）:39-45（in Chinese）.

[10]陈光宇，何健，施蔚锦，等.基于量子混合蛙跳算法的含分布式电源配电网无功优化 [J].电网与清洁能源，2015，31（5）:36-41，46.CHEN Guangyu，HE Jian，SHI Weijin，et al.Reactive poweroptimizationindistributionnetworkwithdistributedgenerators based on quantum shuffled frog leaping algorithm[J].Power System and Clean Energy，2015，31（5）:36-41，46（in Chinese）.

[11]王韶，周鑫.应用层次聚类法和蚁群算法的配电网无功优化[J].电网技术，2011，35（8）：161-167.WANG Shao，ZHOU Xin.Optimization of reactive power in distribution network with hierarchical clustering and ant colonyalgorithm[J].Power System Technology，2011，35（8）：161-167（in Chinese）.

[12]LIU Yutian，MA Ii，ZHANG Jianjun，GA/SA/TS hybrid algorithms for reactive power optimization[C]//IEEE PES Summer Meeting，2000（1）：245-249.

[13]娄素华，吴耀武，熊信银.电力系统无功优化的变尺度混沌优化算法[J].电网技术，2005，29（11）：20-24.LOU Suhua，WU Yaowu，XIONG Xinyin.Mutative scale chaos optimization algorithm for reactive power optimization of power system[J].Power System Technology，2005，29（11）：20-24（in Chinese）.

[14]刘红文，张葛祥.基于改进量子遗传算法的电力系统无功优化[J].电网技术，2008，32（12）：35-38.LIU Hongwen，ZHANG Gexiang.A reactive power optimization method based on improved quantum-inspired genetic algorithm[J].Power System Technology，2008，32（12）：35-38（in Chinese）.

[15]单瑞卿，吕群芳，王建勋，等.基于自适应遗传算法的配电网无功优化[J].电力电容器与无功补偿，2010，31（3）:18-21，57.SHAN Ruiqing，LÜ Qunfang，WANG Jianxun.et al.Reactive power optimization of distribution network based on adaptive genetic algorithm[J].Power Capacitor&Reactive PowerCompensation，2010，31（3）:18-21，57（inChinese）.

[16]HAN K H，KIM H J.Quantum-inspire devolutionary algorithm for a class of combinatorial optimization[J].IEEE Trans on Evolutionary Computation，2002，6（6）：580-593.

[17]HEY T.Quantum computation：an introduction[J].Computing&Engineering Jounal，1996，10（3）.105-112.

[18]赵登福，杨靖，刘昱.基于改进遗传算法的配电网无功优化[J].西安交通大学学报，2001，35（12）：1219-1222.ZHAO Dengfu，YANG Jing，LIU Yu.Reactive power optimization of the radial distribution system based on the improved genetic algorithm[J].Journal of Southwest Jiaotong University，2001，35（12）：1219-1222.

[19]娄素华，李研，吴耀武，等.多目标电网无功优化的量子遗传算法[J].高电压技术，2005，31（9）：69-71.LOU Suhua，LI Yan，WU Yaowu.Multi-objective reactive power optimization using quantum genetic algorithm[J].HighVoltageEngineering，2005，31（9）：69-71（inChinese）.