对2014年高考湖北卷理科第9题的深入探究
刘彦永
(东北师范大学附属中学 130021)
对2014年高考湖北卷理科第9题的深入探究
刘彦永
(东北师范大学附属中学 130021)
本文对一道高考解析几何填空题进行了深入探索,从不同的思路获得多种解法.
试题;解法;探究
2014年高考湖北卷理科第9题,题目虽不新颖,但是内涵丰富,引起了笔者的深入探索和思考.
题目如下:


一、试题分析
本题属于传统题,考查了椭圆和双曲线的定义和性质、正弦定理和余弦定理等知识点.以圆锥曲线为载体,考查了数形结合思想、等价转化能力和函数方程及不等式思想.
二、解法探究
本题解法很多,不同的解法体现不同的思维层次和思考角度,要求考生要有一种勇于探索、敢于实践的精神.

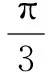
思路二在△F1PF2中由余弦定理得|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|cos∠F1PF2,即(2c)2=m2+n2-2mncos60°=m2+n2-mn.
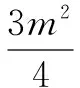


思路三在△F1PF2中,由余弦定理得:
|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|cos∠F1PF2=(|PF1|+|PF2|)2-3|PF1|·|PF2|①,
|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|cos∠F1PF2=(|PF1|-|PF2|)2+|PF1|·|PF2|②.

注此结论也可由如下两种方法得到.
(1)利用椭圆和双曲线的焦点三角形面积公式



(2)利用待定系数法






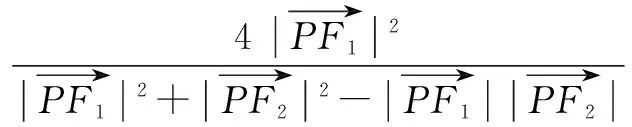

三、试题探源
本题源于人教A版教材选修2-1的62页B组第1题.试题模型来源于课本,体现了高考试题“立足教材,高于教材”的命题原则. 2013年高考浙江理科第9题也是以共焦点的椭圆和双曲线为载体的一道题,相比之下本题增加了思维量和计算量,体现了高考试题“常考常新,推陈出新”的理念.
试题解法的探究仅仅是试题研究的一个开端.对解法的探索是在践行我们所学的知识技能和思想方法,同时也使我们的思维更广阔、思想更深刻.对试题本质的探源,使我们更深刻的认识问题,将新旧解题经历跨时空贯通起来,这又是一个新的开始.
[1]人民教育出版社,课程教材研究所,中学数学课程教材研究开发中心.人教A版数学选修2-1.普通高中数学课程标准试验教科书[M].北京:人民教育出版社,2005.
G632
A
1008-0333(2017)31-0004-02
2017-07-01
刘彦永,北京师范大学硕士,中学一级教师,数学奥林匹克竞赛教练员.
杨惠民]

