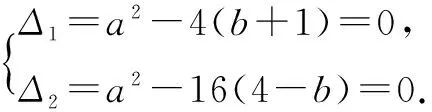谈谈判别式的解题功能
常思源
(河北省唐山市第二中学 063000)
谈谈判别式的解题功能
常思源
(河北省唐山市第二中学 063000)
在高中数学学习中,注重数学思想方法的学习和总结,掌握多种多样的数学方法,这对提高解答数学问题的能力是十分重要的.本文针对数学解题中应用广泛的“判别式”法,列举了它的多种用途,这对提高解题能力具有参考价值.
数学解题;一元二次方程;判别式;功能
一、求值域
例1 已知实数a、b、c满足a+b+c=0,a2+b2+c2=1,则a的取值范围是____.
解将c=-(a+b),代入a2+b2+c2=1中,消去c,再以b为主元,a为参数整理成2b2+2ab+2a2-1=0.
将上式视为关于b的一元二次方程,由b是实数,知该一元二次方程有实根,故Δ=4a2-8(2a2-1)≥0.
点评本例解法中,先消去(c)化三元为二元,再选定主元(b)和待求参数(a),从而构造出一元二次方程,利用判别式非负使问题获解.以上的解题思路自然顺畅,是我们解答数学题的常规策略,是我们每个高中生都应掌握的基本技能.
二、求最值
例2 曲线x2-2xy-3y2=1上的点到坐标原点的距离的最小值为____.

由t(x2-2xy-3y2)=x2+y2,整理成(t-1)x2-2txy-(3t+1)y2=0.
(1)当y=0时,可求得t=1.



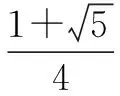
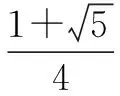

三、证明不等式
例3 设a、b是实数,且a3+b3=2,求证0 而上式中的k2+2k+4的判别式Δk=22-4×1×4=-12<0,故恒有k2+2k+4>0,那么不等式化成k(k-2)≤0(k≠0). 解得0 点评本例解题中先从条件式中通过引入参数k来表达a+b,ab,从而逆用韦达定理构造出一元二次方程,为利用判别式创造了条件.但解题中应关注一些隐含条件(k≠0)(k2+2k+4>0),才能使解题即严谨又简化. Δ1=a2-4(b+1)≥0且Δ2=a2-16(4-b)≥0①. Δ1=a2-4(b+1)≤0且Δ2=a2-16(4-b)≤0②. 由①和②可知有 点评本解法对值域[-1,4]的深层次含义进行挖掘,分别利用方程有实根和不等式恒成立,从两个方面思考,列出两个判别式的不同符号,从而导出两个判别式都为零,充分体现了思维的灵活与广阔性,对判别式的含义理解深邃. 总之,判别式的应用是十分广泛的,以上仅对代数方面的应用略谈几例,实际上,判别式在几何、三角、解析几何等诸多方面都有应用.可以说,判别式法是求解数学问题常用的、广泛的、重要的工具,我们应熟练掌握,善于运用. [1]赵建勋.判别式法解题举例[J].中学生数学(高中),2014(1):15-16. [2]赵兴根.例析反向思维在初中数学解题中的应用[J].福建中学数学,2014(3):42. [3]杨春娟.含参一元二次不等式的解法与恒成立问题[J].中学生数学(高中),2015(2):28. G632 A 1008-0333(2017)31-0040-02 2017-07-01 常思源,河北省唐山市第二中学,在校学生. 杨惠民]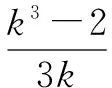
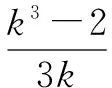
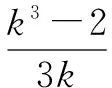
四、求参数的值