道是无圆却有圆——巧构辅助圆解题

孟方明

(浙江省春晖中学 312353)

道是无圆却有圆
——巧构辅助圆解题

孟方明

(浙江省春晖中学 312353)

摘要：圆是高中数学的主干知识，也是高考必考的内容之一．对于以隐性呈现方式的圆的问题，如果不能将圆化隐为显，则往往会陷入繁杂的计算．本文着眼于圆的平面几何性质以及圆的位置关系，通过巧构辅助圆，谈谈如何破解有关圆的问题．

平几性质；位置关系；构造

高中数学中有些问题看似与圆无关，但若能深入挖掘题目中的隐含条件，巧妙地构造辅助圆，然后运用圆的有关知识，便能顺利地建立起条件与结论之间的联系，化隐为显，化繁为简，化难为易，从而“圆”满地解决问题．

一、利用圆的平面几何性质

1.对直径的张角

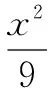
解析由于圆内的点对直径的张角为钝角，因此构造以F1F2为直径的圆，如图1，椭圆与圆相交，结合题意知点P落在弧P1P2以及与x轴对称的劣弧上.联立椭圆方程与圆方程

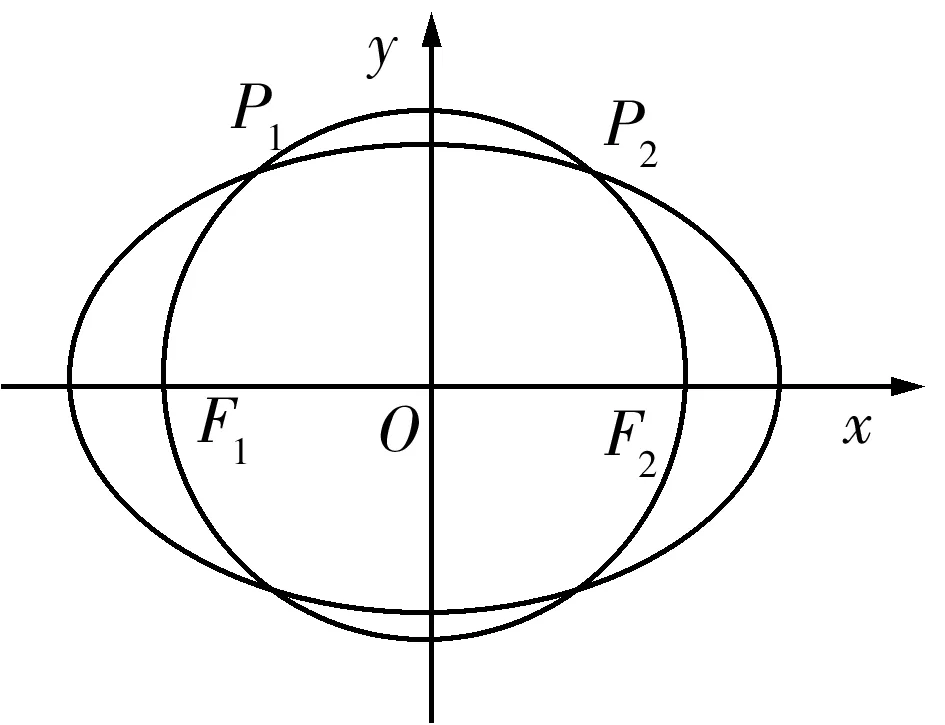
图1

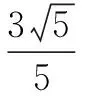
说明设P为平面内一点，AB是圆O的直径，则点P在圆O(不同于A,B)上等价于∠APB=90°；点P在圆O内等价于∠APB>90°;点P在圆O外等价于∠APB<90°．

本题关键是根据题目中的点P对两定点F1,F2为钝角联想到上述圆的基本性质．

2.圆周角定理

(Ⅰ)求椭圆的方程；

(Ⅱ)设P为直线l:x=m(|m|>1)上的动点，使∠F1PF2最大的点记为Q，求点Q的坐标(用m表示)．

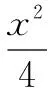
(Ⅱ)不妨设m<0，如图2.

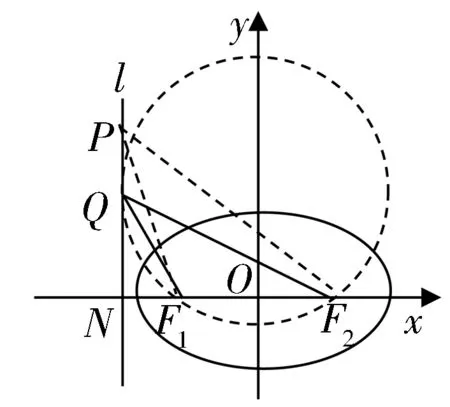
图2

过F1、F2作圆与直线x=m切于点Q.

当点P不同于点Q时，∠F1QF2、∠F1PF2分别为圆周角与圆外角.根据圆周角定理，圆周角大于任一圆外角,即恒有∠F1QF2>∠F1PF2．

设直线l1与x轴交于点N，

由切割线定理知，|NQ|2=|NF1|·|NF2|=(-c-m)(c-m)=m2-c2=m2-1，

说明同圆弧所对圆周角大于圆外角，对某些张角最大值问题，若巧用“两角”关系，则可迅速锁定最值位置．本题关键在于由∠F1QF2恒大于∠F1PF2，构造过点F1、F2且切于点Q的辅助圆，使两角分别成为圆周角与圆外角．与传统函数不等式解法相比，简捷而又创新．

二、利用与圆有关的位置关系

1.点与圆的位置关系

例3 若cosα+cosβ=1，求sinα+sinβ的取值范围．

解析根据三角函数sinα,cosα的定义，构造单位圆，设角α,β的终边与单位圆x2+y2=1分别交于点A,B，则A(cosα,sinα)，B(cosβ,sinβ).

图3

说明若点P在圆C:f(x,y)=0内或圆上，则|PC|≤r(r为⊙C半径)．本题关键是由三角式联想三角函数定义，构造单位圆O，使cosα+cosβ、sinα+sinβ与弦中点P建立联系．

2.直线与圆的位置关系

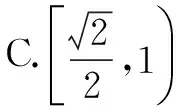
解析由已知，|F1F2|=|F2P|=2c，即点P到定点F2的距离为定值2c，

∴P在以F2为圆心，2c为半径的圆(x-2c)2+y2=4c2上.

∴直线与圆有公共点，

∴a2≤3a2，

故选D．

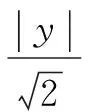
∴|y|≤2，∴ymax=2．

3.圆与圆的位置关系

例6 在坐标平面内与点A(1,2)距离为1，且与点B(3,1)距离为2的直线共有( )．

A.1条 B.2条 C.条 D.4条

解析由题意，到点A(1,2)距离为1的直线是以A为圆心，1为半径的圆的切线，同理，到点B(3,1)距离为2的直线是以B为圆心，2为半径的圆的切线，故与点A(1,2)距离为1，且与点B(3,1)距离为2的直线是⊙A和⊙B的公切线.

∴|r1-r2|<|AB|

∴公切线有2条，选B．

说明两圆在不同的位置关系下，公切线的条数各不相同，若两圆相交，则公切线有两条．本题关键是由到定点距离为定长的直线，浮想到圆的切线，此时再结合两圆位置关系，则获得巧解，可谓不拘一格、独具匠心．

[1]人民教育出版社，课程教材研究所，中学数学课程教材研究开发中心.人教A版数学选修2-1.普通高中数学课程标准试验教科书[M].北京：人民教育出版社，2005.

G632

A

1008-0333(2017)31-0006-02

2017-07-01

孟方明(1979-)，男，浙江绍兴人，大学本科，中学高级教师，从事高中数学教学研究．

杨惠民]