直径为偶数的二部图的最小EDS极图

雷勇,杨爱民，杨丽英

(1.吕梁学院 数学系,山西 吕梁 033000;2.山西大学 数学科学学院,山西 太原 030006;3.山西大学 商务学院信息学院,山西 太原 030031)

直径为偶数的二部图的最小EDS极图

雷勇1,杨爱民2，杨丽英3

(1.吕梁学院 数学系,山西 吕梁 033000;2.山西大学 数学科学学院,山西 太原 030006;3.山西大学 商务学院信息学院,山西 太原 030031)

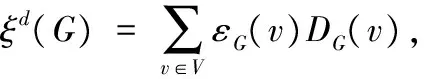
距离;直径;二部图;EDS

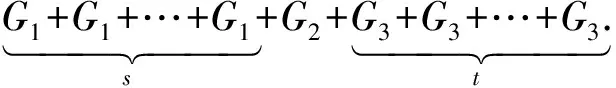
图的拓扑指数能够很好地刻画有机物分子的生物和物理性质,因而倍受关注。 Wiener指数可能是最早提出的基于距离的一个拓扑指数,其定义为

它与分子的许多物理、化学指标有着密切的关系[3],2002年,Gupta,Singh和Madan[4]提出了另一个比使用Wiener指数刻画有机物性质更好的指数──偏心距离和,简记为EDS,其定义为

(v).

近年来关于图的EDS指数有许多重要的结果[4-13]。 2015年,Li等[1]确定了对集为q的连通二部图的EDS下界且给出直径为奇数且具有最小EDS的连通二部图的极图,并提出三个重要的开放性问题,下面是第一个问题。

问题 如何确定直径为偶数且具有最小EDS的连通二部图的极图?

下面我们首先介绍几个重要的引理,最后给出这个问题的结果。

引理1[5]G是一个n阶连通图,且G≠Kn,则对于任意边e∉E有ξd(G)>ξd(G+e).

引理2[14]G是一个直径为d的n阶连通二部图,设dG(v0,vd)=d,P=v0v1…vd是一条v0,vd之间的最短路,Vi={v|dG(v0,v)=i},则Vi(i=0,1,…，d)的诱导子图是空图。

引理3G是一个直径为d(≥4)且具有最小EDS的n阶连通二部图,设dG(v0,vd)=d,P=v0v1…vd是一条v0,vd之间的最短路,Vi={v|dG(v0,v)=i},则Vi∪Vi+1(i=0,1,…,d-1)的诱导子图是完全二部图且|Vd|=1.

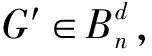
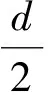
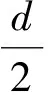
DG(v)=DG′(v)-2,v∈V0∪…∪Vr-1;

DG(v)=DG′(v)+2,v∈Vr+3∪…∪Vd;

DG(v)=DG′(v),v∈Vr∪Vr+1∪Vr+2;

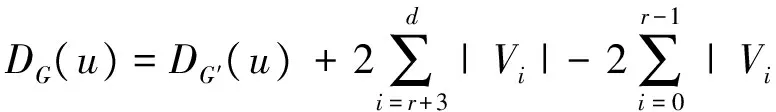
由EDS的定义可知

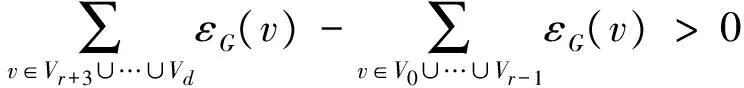
引理5G是一个直径为偶数d(≥4)且具有最小EDS的n阶连通二部图,设dG(v0,vd)=d,P=v0v1…vd是一条v0,vd之间的最短路,Vi={v|dG(v0,v)=i},则

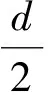
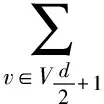
由引理1-5可得到下面的结论。

定理G是一个直径为偶数d(≥4)且具有最小EDS的n阶连通二部图,则

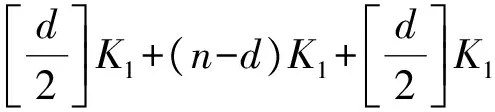
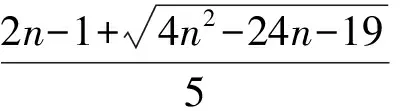
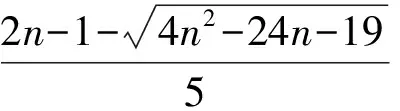
[1] Li S C,Wu Y Y,Sun L L.On the Minimum Eccentric Distance Sum of Bipartite Graphs with Some Given Parameters[J].JMathAnalAppl,2015,430:1149-1162.DOI:10.1016/j.jmaa.2015. 05.032.

[2] Bondy J A,Murty U S R.Graph Theory with Applications[M].New York:Macmillan London and Elsevier,1976.

[3] Dobrynin A A,Entringer R,Gutman I.Wiener Index of Trees:Theory and Applications[J].ActaApplMath,2001,66:211-249.

[4] Gupta S,Singh M,Madan A K.Eccentric Distance Sum:A Novel Graph Invariant for Predicting Biological and Physical Properties[J].JMathAnalAppl,2002,275:386-401.

[5] Yu G H,Feng L H,Ilic＇ A.On the Eccentric Distance Sum of Trees and Unicyclic Graphs[J].JMathAnalAppl,2011,375:99-107.DOI:10.1016/j.jmaa.2010.08.054.

[6] Hua H B,Zhang S G,Xu K X.Further Results on the Eccentric Distance Sum[J].DiscreteApplMath,2012,160:170-180.DOI:10.1016/j.dam.2011.10.002.

[7] Mao L Y,Cao Q Q,Cui N,etal.On the Extremal Values of the Eccentric Distance Sum of Trees[J].DiscreteApplMath,2015,186:199-206.DOI:10.1016/j.dam.2015.01.042.

[8] Mukungunugwa V,Mukwembi S.On Eccentric Distance Sum and Minimum Degree[J].DiscreteApplMath,2014,175:55-61.DOI:10.1016/j.dam.2014.05.019.

[9] Ilic＇ A,Yu G H,Feng L H.On the Eccentric Distance Sum of Graphs[J].JMathAnalAppl,2011,381:590-600.DOI:10.1016/j.jmaa.2011.02.086.

[10] Geng X Y,Li S C,Zhang M.Extremal Values on the Eccentric Distance Sum of Trees[J].DiscreteApplMath,2013,161:2427-2439.DOI:10.1016/j.dam.2013.05.023.

[11] Li S C,Zhang M,Yu G H,etal.On the Extremal Values of the Eccentric Distance sum of Trees[J].JMathAnalAppl,2012,390:99-112.DOI:10.1016/j.jmaa.2012Z01.022.

[12] Hua H B,Xu K X,Wen S.A Short and Unified Proof of Yu et al.’s Two Results on the Eccentric Distance Sum[J].JMathAnalAppl,2011,382:364-366.DOI:10.1016/j.jmaa. 2011.04.054.

[13] Azari M,Iranmanesh A.Computing the Eccentric-distance Sum for Graph Operations[J].DiscreteApplMath,2013,161:2827-2840.DOI:10.1016/j.dam.2013.06.003.

[14] Pisanski T,erovik J.Edge-contributions of Some Topological Indices and Arboreality of Molecular Graphs[J].ArsMathContemp,2009,2:49-58.

ExtremalBipartiteGraphsofGivenEvenDiameterHavingMinimalEDS

LEI Yong1，YANG Aimin2，YANG Liying3

(1.DepartmentofMathematic,LvliangUniversity,Lvliang,Shanxi033000,China;2.SchoolofMathematicalSciences,ShanxiUniversity,Taiyuan,Shanxi030006,China;3.SchoolofInformation,BusinessCollegeofShanxiUniversity,Taiyuan,Shanxi030031,China)

distance;diameter;bipartite graph;EDS

10.13451/j.cnki.shanxi.univ(nat.sci.).2017.04.006

2016-12-05；

2017-01-13

吕梁学院教学改革项目(JYYBZ201410)；山西省重点研发计划项目(201603D321112)

雷勇(1981-),男,山西兴县人,研究方向:图论及其应用。E-mail:1050506548@qq.com

O157.5

A

0253-2395(2017)04-0717-04