一种基于偏微分方程和Canny算子的图像分割方法

侯守明,王阳,唐琪博,张玉珍

(河南理工大学 计算机科学与技术学院,河南 焦作 454000)

一种基于偏微分方程和Canny算子的图像分割方法

侯守明,王阳,唐琪博,张玉珍

(河南理工大学 计算机科学与技术学院,河南 焦作 454000)

边缘轮廓的分割与提取是基于图像处理方法检测线束端子压接质量的前提。针对传统图像处理方法自动提取线束端子截面边界轮廓不准确的问题,以偏微分理论为基础,结合Canny算子边缘检测方法,提出一种基于偏微分方程和Canny算子的边缘检测模型。利用卷积边界自动填充图像边界,通过梯度非极大值抑制选择阈值最大化区分目标和背景。理论研究和实验结果表明,该模型不仅能比较准确地检测图像边缘轮廓,而且对噪声、模糊有一定的抑制作用。该模型已经应用在线束端子断面轮廓自动测量系统中并准确地提取边缘轮廓。

偏微分方程;Canny算子;线束端子;边缘检测

0 引言

图像的主要信息集中在它的边缘、细节和纹理等特征中,而这些特征不仅对于图像的视觉效果意义重大,而且对于图像分析和理解等图像后续工作任务来说也是非常重要的。边缘检测作为数字图像处理的重要内容之一,其目的是提取图像边缘轮廓信息,剔除不相关的信息,从而极大地减小分析的数据量[1]。图像边缘检测是数字图像处理的重要内容,是进行图像分割、图像分析、物体识别等深层次处理的关键步骤;边缘提取的目的就是把目标物体或者人们感兴趣的部分从图像中分离出来,同时得到相应的目标物体的边缘,通过边缘检测可以保留物体边界形态的结构信息,极大地降低图像处理的数据量,从而简化图像分析的过程[2-3]。

汽车线束端子压接质量的检测是保证汽车安全性、可靠性,提高汽车整车质量的关键因素之一。通过提取压接端子断面轮廓,将测得参数同设定的标准参数进行比较,以此来判断端子断面压接质量是否合格,并自动输出测试结果,可以满足线束生产制造企业端子压接质量检测的需求,并且大大减轻测试人员的劳动强度,提高工作效率,保证产品质量。线束端子断面轮廓的自动提取是端子断面检测仪器的核心技术,现有端子断面测量系统主要采用传统的边缘检测方法实现端子断面轮廓的自动检测,效果并不令人满意;如不能实现自动检测,工作人员必须采用人机交互(手描)的方式提取轮廓,劳动强度很大。如何采用适合端子断面图像的图像分割模型提高自动检测的成功率便成为系统开发的关键难题。

线束端子断面轮廓具有连续性好、噪声干扰大、边缘强弱对比度明显等显著特点,经实验比对,常用的边缘检测算子,如Robert算子、Sobel算子、Prewitt算子、LOG(Laplace of Gaussian)算子、DOG(Difference of Gaussian)、Canny微分算子等[4-7],在线束端子断面轮廓批量检测中都不是具有绝对优势的方法,在图像的抗噪声、图像边缘的定位情况、图像部分边缘是否可以检测出,以及算法运行的速度等方面,各自存在优缺点。在现有的这些边缘检测算子中,Canny算子是相对较好的一种,采用基于梯度赋值的双阈值法检测和连接边缘时,相比较其他算子而言能够比较准确地检测出边缘轮廓,可以抑制噪声。但是对于高噪声的模糊图像,Canny算子在抑制噪声的同时往往错过了一些低强度的边缘,而一些高强度的噪声被检测为边缘。

将边缘检测算子与其他交叉学科(如神经网络、形态学算法等)相结合对图像进行分割[8-9]是解决上述问题的一个比较理想的方法。目前,常用的图像目标分割模型可分为:基于聚类的方法如Mean-Shift方法，基于统计的方法如Markov随机场方法，基于数学形态的方法如分水岭算法[10],基于水平集方法和几何式蛇模型等方法,而基于偏微分方程[11-12]的分割模型已成为图像分割研究领域的热点之一,并在医学图像[13]、车牌识别[14]、人脸检测[15]等领域得到了广泛应用。基于偏微分方程方法主要是数学方法在空间域内的图像处理中的应用,使用空间域内像素点灰度的一阶或二阶微分方程表征图像中的区域边界等边缘特征,通过建立偏微分方程的数学模型以及模型分析最终达到分割的目的。其优势主要体现在:偏微分方法的图像分割方法以连续的图像模型为基础,运用连续的微分对图像进行滤波,采用离散的网格化,使对图像的目标处理和分析更加容易实现;以闭合曲线为基础,图像目标分割可以达到亚像素的精度;采用水平集方法可以得到较精准的结果,可以解决目标的合并与分离引起的拓扑结构变化问题。

本文提出融合偏微分方程和Canny算子的方法实现压接端子断面轮廓提取,考虑线束端子图像特点,优势互补,可以大大提高线束压接端子断面轮廓的有效识别率。

1 基于PDE的边缘分割技术

基于偏微分方程的图像边缘分割方法,其基本思想是根据图像分割的要求构建相应的微分模型[16],然后求解该微分方程,方程的解就是所希望的结果。目前基于偏微分方程的图像分割主要是采用活动轮廓模型[17]来实现,参数活动轮廓模型难以处理拓扑结构的变换,而以水平集为代表的几何活动轮廓模型受噪声干扰,如果图像噪声很大,影响活动轮廓线演化,或者产生不精确的定位。为了改进参数活动轮廓模型和以水平集为代表的几何活动轮廓模型的不足,Chan和Vese提出了一种基于M-S的简化分割模型[18](简称C-V模型)。该模型假定图像I(x,y)被活动轮廓线C划分为内部(inside)和外部(outside)两个同质区域,各个等值部分的平均灰度为C0和Cb,以最小化能量函数FMS为目的,寻找具有最小差异的待分割图像和原始图像。

(1.1)

基于M-S分割模型的能量函数如下:其中C是闭合活动轮廓线,L(C)是活动轮廓线C边缘长度,S0(C)是活动轮廓线C的内部区域面积,μ、ν、λ0、λb是相应的权重系数,C0和Cb代表平均灰度,当轮廓线C位于两个同质区域边界时F(C,C0,Cb)取得最小值:

(1.2)

M-S的简化分割模型不再依赖图像梯度信息,而是利用全图的能量信息,所以可以得到全局最优的分割结果,不用太关注初始曲线位置;由于不利用图像梯度,因此对噪声不是非常敏感,无须分割前进行去噪处理。最后,通过水平集方法来求解M-S的简化分割模型:首先假设是根据初始活动轮廓线C0的符号距离函数为φ,{C0|φ0(x,y)=0}且φ[inside(C)]>0,φ[outside(C)]<0,其中H(z)为Heaviside函数,δ(x)为Dirac函数,定义如下所示:

(1.3)

但是在实际应用中采用规范化的Heaviside函数和Dirac函数,其定义如下:

(1.4)

同时可以得出,其中L(C)是闭合轮廓线C的边缘长度,Ω为灰度图像I(x,y)的定义域,φ(x,y)为水平集函数:

(1.5)

将(1.5)代入(1.2),可推出:

(φ)|φ|dxdy+

(1.6)

通过最优化(1.2)式,最终得到轮廓线C的位置以及未知数C0(φ)和Cb(φ),根据梯度下降法及使用欧拉-拉格朗日方法求解式(1.6)可得:

(1.7)

通过数值化求解式(1.7),可以计算出图像中每个点的φ值,更新水平集,最终使曲线演化到物体的边缘,达到分割的目的。

2 基于PDE和Canny算子的边缘检测

2.1 Canny算子边缘检测

相比其他算子而言,Canny算子具有很好的边缘检测性能。Canny算子不容易受噪声影响,能够在噪声和边缘检测间取得较好的平衡,进而检测出真正的边缘。其算法思想是先将图像使用高斯函数进行平滑[19-20],再由一阶微分的极大值确定边缘点。Canny边缘检测算子步骤如下:

第一步:使用高斯函数G(x,y,σ)构造滤波器得到平滑图像。

(2.1)

用高斯函数G(x,y,σ)对图像f(x,y)进行滤波:g(x,y)=G(x,y,σ)·f(x,y)。其中,σ是高斯函数的标准差主要用来控制平滑度。

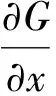
(2.2)

(2.3)

通过改变高斯函数标准差σ来实现对高斯窗口的大小调整。

(2.4)

第三步:对梯度幅值采用非极大值抑制,然后采用双阈值法对图像进行分割。首先设置两个阈值,上限和下限。如果一个像素的梯度大于上限阈值,则被认为是边缘像素,如果低于下限阈值,则被抛弃,如果介于二者之间,只有当其与高于上限阈值的像素连接时才会被接受。

第四步:边缘连接。

2.2 融合Canny算子和PDE模型的边缘检测

偏微分方程的C-V模型是全图像的范围[21],能够保证边缘计算的全局优化特点,结合Canny算子边缘检测的优点,构建基于Canny算子和PDE的模型从而达到图像边缘轮廓的准确提取[22]。

设闭合曲线C(p,t):0≤p≤1在t时刻隐式函数为φ(x,y,t),则φ的零水平集的平面闭合曲线的偏微分方程为

(2.5)

求其全微分得:

φ·+=0

(2.6)

(2.7)

将式(2.5)和(2.7)带入式(2.6),通过整理上式可以得到

φt=-φV(K)N=φV(K)=V(K)|φ|

(2.8)

通过式(2.8)可计算出曲率

K=·=

(2.9)

由偏微分在时间边界t位置通过φ(x,t)=0得φ(x,t)满足

(2.10)

用Canny算子的结果A(x,y)来替代曲线平面(x,y)即:φ(A(x,y),t)带入(2.10)式得零水平曲线随时间演化方程式:

(2.11)

其中

(2.12)

将式(2.12)带入(2.11)式得:

(2.13)

其中Gσ表示方差为σ高斯函数,*为卷积,v为常数。

采用非极大值抑制技术和边缘连接技术,抑制噪音的影响,得到高精度的细边缘。通过使用上述Canny算子和PDE技术融合模型,能够克服传统图像分割算法对噪声敏感、抗干扰差的缺点,可以很好地区分目标和背景,进而提取边界轮廓。

3 实验结果与分析

在上述研究的基础上,基于Microsoft Visual Studio2010开发平台,采用C++和OpenCV函数库,在Windows7平台系统上开发了压接端子断面自动测量系统。

本文实验采用的是从国内某汽车线束生产厂家通过工业用显微镜采集的线束端子断面图像检测库中抽取的典型图像,放大倍数为10倍。测试机器配置为:i5-4590,4G内存,技嘉750显卡2G显存,1T硬盘,windows7操作系统。

首先采用传统算子进行边缘检测,测试结果如下:图1为对比度明显的情况下传统算子的检测结果,图2为噪声和边界模糊情况下传统算子检测的结果。从图1和图2可以看出,传统的边缘检测算子检测的不准确性,而且在噪声干扰、边界模糊等情况下会检测出多余的图像信息。其次,根据图像梯度选取双阈值进行边缘检测:图3(a)是第一幅原图在阈值t1=63,t2=214情况下检测的结果;图3(b)是第二幅原图在阈值t1=59,t2=106情况下检测的结果。从检测结果图可以看到Canny算子检测的端子断面轮廓相对于传统算子比较准确,抗干扰性强。

通过实验对比发现,传统的边缘检测算子在噪声干扰、边缘模糊的情况下检测的边缘轮廓不准确,而Canny算子通过上下阈值的设置可以准确地检测出边缘轮廓。

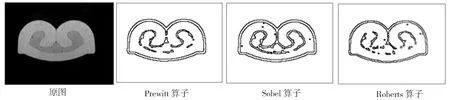
Fig.1 Detection results of traditional operators under obvious contrast图1 对比度明显情况下传统算子的检测结果

Fig.2 Detection results of traditional operators in the presence of boundary blur and noise图2 边界模糊和噪声干扰情况下传统算子的检测结果

Fig.3 Detection results of Canny operator under different threshold t图3 在不同阈值t情况下Canny算子检测结果

最后,采用基于PDE和Canny算子实现端子断面内外轮廓自动检测,算法思想如下:

(1)根据图像像素的位置、灰度和梯度信息,判断边界所在的大致位置,并依次进行图像滤波和边缘检测。

(2)在图像滤波过程中,根据像素分布情况,利用灰度加权平均的方法进行噪声消除。在构造加权系数的过程中,利用图像的梯度方向和大小信息,自适应决定所需要的权重系数,使图像局部区域达到分片常数的效果。通过这样的处理,可以有效消除图像中包含的噪声,并同时很好地保持边界,以保证提取边界时的准确率。

(3)在边缘检测中,在图像去噪的基础上,利用Canny算子代替曲线演化平面寻找物体边界。演化的动力来源于图像的内部结构,即灰度分布。为了有效地处理曲线分裂和融合,采用水平集技术将曲线隐含在高一维的水平集当中,利用三维空间的连续变化来得到二维空间的曲线不规则变化。当曲线达到边界并停止时,即得到物体的边缘轮廓。

本文分别对端子断面的内外轮廓进行检测,测试结果如下:图4-图6分别在对比度明显、边界模糊、噪声干扰等情况下,得到的检测结果。图中(a)放大10倍的原始图片,(b)为内轮廓检测结果,(c)为外轮廓检测结果。由实验结果可以看出:在对比度理想、边界模糊、主要轮廓有干涉等三种情况下,采用PDE模型和Canny算子融合检测算法,都能得到满意的轮廓检测结果,轮廓自动检测的时间在可允许范围之内。

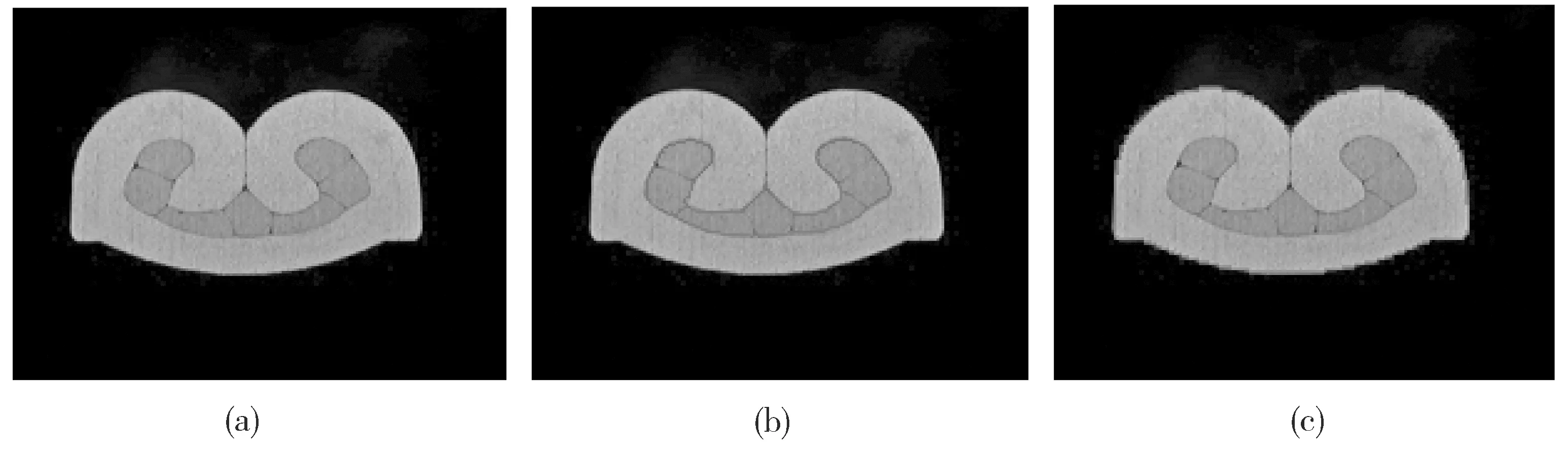
Fig.4 Segmentation results under contrast ideal conditions based on Canny Operator and PDE图4 基于Canny算子和PDE在对比度理想情况下的分割结果

Fig.5 Segmentation results when the boundary is fuzzy based on Canny operator and PDE图5 基于Canny算子和PDE在边界比较模糊时的分割效果

Fig.6 Segmentation Results in the presence of interference of the main contours based on Canny operator and PDE图6 基于Canny算子和PDE在主要轮廓有干涉情况下的分割效果

4 结论

本文以线束端子图像轮廓的自动提取为研究对象,分析了PDE模型、Canny边缘检测算子实现的原理,构建了基于PDE和Canny算子的融合检测模型,并在检测的准确性、稳定性上同传统的边缘检测算法测试结果进行实验验证,可以得出如下结论。

(1)Canny算子通过二维高斯函数和卷积操作处理图像,采用非极大值抑制技术和连接技术,能够得到高精度的细边缘。

(2)偏微分方法采用广义的连续二维函数建立图像能量模型,然后对函数求导求积分,使图像处理更加规范,PDE方法可以在图像处理中达到双重功效,在图像去噪的模型中可以较好地保护边缘信息,在图像增强模型中可以去除噪声,使得图像分割的准确性和稳定性大幅度提升,在图像分割和轮廓提取中,具有良好的实用性和鲁棒性。

(3)基于PDE和Canny算子的模型保持了Canny算子的优点,比Canny算子的适应范围广,能分割对比度较明显、模糊不均匀的图像,抗噪性较强,对初始轮廓的大小不敏感,而且可以较准确地分割内外轮廓。

[1] 宋熙煜,周利莉,李中国,等.图像分割中的超像素方法研究综述[J].中国图象图形学报,2015，5:599-608.

[2] Liu J，Tang Q，Wang Y,etal.Defects’ Geometric Feature Recognition based on Infrared Image Edge Detection[J].InfraredPhysicsandTechnology,2014，67:387-360.DOI:10.1016/j.infrared.2014.07.024.

[3] 杨婷婷,顾梅花,章为川,等.彩色图像边缘检测研究综述[J].计算机应用研究,2015,9:2566-2571.

[4] Koyuncu I，Cetin O，Katircioglu F，etal.Edge Detection Application with FPGA Based Sobel Operator[C]∥2015 23rd Signal Processing and Communications Applications Conference,SIU 2015-Proceedings,June 19,2015:1829-1832.DOI:10.1109/SIU.2015.7130211.

[5] Nashat S,Abdullah A,Abdullah M Z.Unimodal Thresholding for Laplacian-based Canny-Deriche Filter[J].PatternRecognitionLetters,2012,10(33):1269-1286.DOI:10.1016/j.patrec.2012.03.023.

[6] 夏清,陈亚凯,张振鑫,等.基于Laplace算子和灰色理论的热红外影像边缘检测[J].红外技术,2014(5):377-380+388.

[7] 张桂梅,孙晓旭,陈彬彬,等.结合分数阶微分和Canny算子的边缘检测[J].中国图象图形学报,2016(8):1028-1038.

[8] 李强强,黎蔚.一种改进的桥梁图像分水岭分割算法[J].计算机工程与科学,2015(3):605-610.

[9] 李杰,苗长云,武志刚,等.基于数学形态学的图像边缘检测算法的研究[J].计算机科学,2012(S1):546-548.

[10] 钮圣虓,王盛,杨晶晶,等.完全基于边缘信息的快速图像分割算法[J].计算机辅助设计与图形学学报,2012(11):1410-1419.

[11] Ci M，Hou T Y，Shi Z.A Multiscale Model Reduction Method for Partial Differential Equations[J].ESAIMMathModelNumerAnal,2014,2(48):1449-1474.

[12] 丁畅,尹清波,鲁明羽.数字图像处理中的偏微分方程方法综述[J].计算机科学,2013(S2):341-346.

[13] Mikula K,Peyrieras N,Remesikova M,etal.Segmentation of 3D Cell Membrane Images by PDE Methods and Its Applications[J].ComputersinBiologyandMedicine,2011,41:326-339.DOI:10.1016/j.compbiomed.2011.03.010.

[14] Zheng L,He X,Samali B,etal.An Algorithm for Accuracy Enhancement of License Plate Recognition[J].JournalofComputerandSystemSciences,2013,2(79):245-255.DOI:10.1016/j.jcss.2012.05.006.

[15] Zhao Y,Liu Y,Liu Y,etal.Face Recognition from a Single Registered Image for Conference Socializing[J].ExpertSystemswithApplications,2015,3(42):973-979.DOI:10.1016/j.eswa.2014.08.016.

[16] Long H V,Son N T,Ha N T,etal.The Existence and Uniqueness of Fuzzy Solutions for Hyperbolic Partial Differential Equations[J].FuzzyOptimizationandDecisionMaking,2014(13):435-462.DOI:10.1007/s10700-014-9186-0.

[17] 文乔农,徐双,万遂人.医学噪声图像分割的分解与活动轮廓方法[J].计算机辅助设计与图形学学报,2011(11):1882-1889.

[18] Alfonso V.The Mumford-Shah Variational Model for Image Segmentation:An Overview of the Theory,Implementation and use[J].ISPRSJournalofPhotogrammetryandRemoteSensin,2012,69:50-64.DOI:10.1016/j.isprsjprs.2012.02.005.

[19] Cope R K,Rockett P I.Efficacy of Gaussian Smoothing in Canny Edge Detector[J].ElectronicsLetters,2000,19(36):1615-1617.DOI:10.1049/el:20001138.

[20] 孙智鹏,邵仙鹤,王翥,等.改进的自适应Canny边缘检测算法[J].电测与仪表,2016(6):17-21.

[21] 侯守明,唐琪博,谷孝卫.基于C-V模型的线束端子断面测量系统设计[J].测控技术,2015(10):42-45+49.

[22] 王小俊,刘旭敏,关永.基于改进Canny算子的图像边缘检测算法[J]. 计算机工程,2012(14):196-198+202.

CrimpTerminalsSectionalContourExtractionBasedonPartialDifferentialEquationandCannyOperator

HOU Shouming,WANG Yang,TANG Qibo,ZHANG Yuzhen

(SchoolofComputerScienceandTechnology,HenanPolytechnicUniversity,Jiaozuo454000,China)

The segmentation and extraction of edge contour are the precondition of detecting the crimping quality of wire harness terminal based on image processing method.For the low accuracy problem of the traditional automatic extraction of harness terminal section contour methods,a new method is proposed based on partial differential theory and Canny operator edge detection method to achieve better results.In this model, the boundary of the image is automatically filled with the convolution boundary, and the selection threshold is suppressed by the non-maxima of the gradient to maximize the discrimination between the target and the background.The theoretical research and experimental results show that the model can not only detect image edge contours more accurately, but also suppress noise and blur.The model was applied in the harness terminal section contour automatic measurement system and accurately extract the edge profile.

partial differential equation;Canny operator;harness terminal;edge detection

10.13451/j.cnki.shanxi.univ(nat.sci.).2017.04.003

2017-06-02；

2017-08-09

国家自然科学基金(61503124)；河南省科技攻关项目(172102210273;162102310090)

侯守明(1972-)，男，河南焦作人，教授，博士。主要研究方向：CAD/CG，虚拟现实与仿真。E-mail:86865346@qq.com

TP391.41

A

0253-2395(2017)04-0676-07