常数变易法的教学探讨
徐术伟,裴丽敏
(1.嘉兴学院 数理与信息工程学院,浙江 嘉兴 314001;2.嘉兴技师学院 商贸旅游系,浙江 嘉兴 314033)
常数变易法的教学探讨
徐术伟1,裴丽敏2
(1.嘉兴学院 数理与信息工程学院,浙江 嘉兴 314001;2.嘉兴技师学院 商贸旅游系,浙江 嘉兴 314033)
本文主要探索如何通过一阶线性常微分方程和二阶线性常微分方程的通解中任意常数,让学生深刻理解常数变易法,并且讨论常数变易法和积分因子法之间的联系,从而加深对常数变易法的理解、掌握和运用.
常数变易法;微分方程;通解;积分因子法
数学的教学应该注重培养学生思考问题的方式和思维过程,这样才可以让学生真正了解和掌握解决问题的办法.在《高等数学》和《常微分方程》的教学中,常数变易法是一种非常有效并且具有创造性的求解方程的办法.但是教材对常数变易法并没有进行深入探讨,对其原理缺少详细说明,学生往往只看到表面问题,不能深刻理解其本质.我们主要通过一阶线性常微分方程和二阶线性常微分方程的通解中任意常数C来让学生深刻理解常数变易法的本质,并且讨论常数变易法和积分因子法之间的联系,从而加深对常数变易法的理解、掌握和运用.
1 一阶线性常微分方程的常数变易法
形如y'+p(x)y=q(x)的方程称为一阶线性常微分方程,式中p(x)、q(x)为已知函数.若q(x)=0;称此方程为一阶线性齐次微分方程.若q(x)≠0;称此方程为一阶线性非齐次微分方程.下面我们通过一阶线性常微分方程的求解来介绍常数变易法[1-3].

通过分离变量法可以得到其通解为:

将上式两端进行积分,可以得到下面式子:

由于y是x的未知函数,不妨记

代入式子(6)得

其中φ(x)为待定函数,记

则式(8)可写为

其中C(x)为待定函数.

将上述求解过程进行比较,可以发现方程(4)的通解(10)中,关于待定函数C(x)占据了通解(3)中C的位置.这样也就很好解释了为什么称此方法为常数变易法,即非齐次线性方程(4)与它对应的齐次线性方程(1)的通解之间的联系与区别之处.另外,我们在讲授此过程时,应当先从利用分离变量法求解一阶线性齐次常微分方程的解开始,然后继续考虑一阶线性非齐次常微分方程的解.但是在讲授一阶线性非齐次常微分方程的求解时,应当注意不应该直接把一阶线性齐次常微分方程的通解(3)中变为C(x),而是让学生体会继续沿着求解一阶线性齐次常微分方程的思路,可以给出一阶线性非齐次常微分方程的形式通解(10).一般来说,方程(4)左端的和式不是一个完全微分式.但我们知道,并非任何含有y'和y一次二项式都不是全微分式.此形式通解(10)刚好是此特殊情况.其实后面从一阶线性非齐次微分方程出发,利用积分因子方法,给出形式通解(10),可以启发学生思维,是一种很容易接受并且具有一些创造力的办法.
2 二阶线性常微分方程的常数变易法
y"+p(x)y'+q(x)y=f(x)称为二阶非齐次线性微分方程,y"+p(x)y'+q(x)y=0称为y"+p(x)y'+q(x)y=f(x)对应的二阶线性齐次微分方程,其中p(x),q(x),f(x)都是关于x的已知连续函数.
下面考虑二阶线性常微分方程[1-3][5]

的通解结构,其对应的齐次线性微分方程为

首先设方程(14)的通解为y=c1y1+c2y2,其中c1,c2为任意常数,且y1,y2是线性无关.所以利用线性微分方程的基本理论只要得到方程(15)的一个特解,就可以了.接下来,考虑利用常数变易法,不妨设其解具有以下形式:

把y(x)=c1(x)y1(x)+c2(x)y2(x)代入方程(14),可得如下方程组:
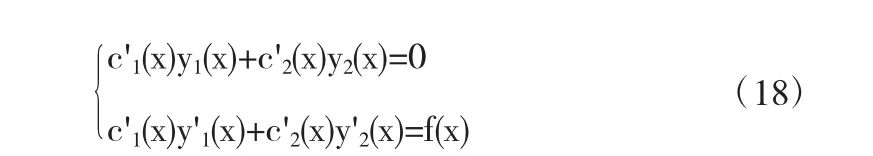
由于y1(x),y2(x)线性无关,其系数行列式

解得:

则方程(14)的通解:
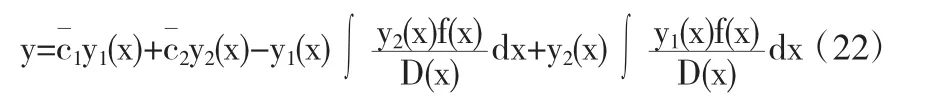
学生在学习的过程中,对二阶线性常系数方程的常数变易法,会感觉到为什么可以设其通解为式(16),并且添加补充条件(17)后其还是非齐次方程(14)的通解.首先我们在讲授时,应当回答学生根据前面一阶线性常微分方程的常数变易法的学习,可以知道二阶非齐次线性常微分方程具有(16)的形式通解.并且补充条件只是方便于后面的求解,至于其仍然为二阶非齐次线性常微分方程(14)的通解,这主要是基于线性微分方程的基本理论所决定的.由于为任意常数,并且y1,y2是齐次方程(15)线性无关解.另外,当时,则知式子(22)中的y依然为方程(14)的解,即y是y"+p(x)y'+q(x)y=f(x)的一个特解,所以y=c1y1+c2y2+y3是y"+p(x)y'+q(x)y=f(x)的通解.其实这也是数学学习的重要作用,可以很好地启发学生思维.虽然常数变易法很简单,但是它给出了一些超出你想象的结果.不过,随着你的知识和理解问题能力的提高,这些想象不到的问题,也就变成了自然,同时你也就得到了很好的锻炼和提高.
其实对于二阶非齐次线性常微分方程的求解还有积分因子法[1-4],这种积分因子的办法是基于前面学习的一阶线性常微分方程的结果.这个结果也可以很好地让学生理解为什么可以把二阶非齐次线性常微分方程(14)的通解写成式子(16).
通过上面一阶和二阶线性常微分方程的常数变易法的学习,学生就可以很好地体会其基本含义,并且这种方法可以推广到高阶线性常微分方程,也对于偏微分方程的求解具有一定借鉴意义.
〔1〕王高雄,周之铭,朱思铭,王涛松.常微分方程[M].北京:高等教育出版社,1983.
〔2〕丁同仁.常微分方程定性方法的应用[M].北京:北京大学出版社,1987.
〔3〕同济大学数学教研室编.高等数学[M]北京:高等教育出版社,2003.
〔4〕李姝菲,赵明.二阶线性微分方程解的讨论[J].吉林师范学院学报,1998(19):21-24.
〔5〕王奕挺,胡良根,张晓敏.常数变易法的探究式教学研究[J].高等数学研究,2015(18):7-9.
O175.1
A
1673-260X(2017)12-0007-02
2017-09-19
嘉兴学院科研启动项目(70515020)

