拓展性内容的教学设计与建议

陆明

（浙江省杭州市滨江区滨兰实验学校）

拓展性内容的教学设计与建议

陆明

（浙江省杭州市滨江区滨兰实验学校）

文章将浙教版教材中的拓展性课程整理分成四类：学科拓展，人文历史，操作活动，专题学习.以拓展性课程“格点多边形的面积探究”为例，整理出拓展性课程的开展思路，并提出了人文历史材料的思想化与学科拓展、操作活动材料探究化等教学建议.

拓展性课程；格点多边形；教学建议

一、引言

拓展性课程是在建设与实施选修课程和活动课程的过程中逐步发展形成的一种功能性课程，改变了学校教育“千人一面，万人同一张课程表”的培养模式，改变了基础教育课程脱离时代和社会发展要求、脱离学生的兴趣爱好、忽视创新精神和实践能力培养的状况.拓展性课程以培养学生的主体意识、完善学生的认知结构、改善学习方式、提高学生自我管理和选择学习的能力为宗旨，故而着力开发、建设以及完善拓展性课程体系迫在眉睫.

二、基于教材的拓展性课程的分类

拓展性课程内容在教材中占有一定的份量，其内容也涉及到多学科、多角度.按课程来分，分别是：横向拓展课程和纵向拓展课程两种.再往细致来分，按内容分，横向拓展课程包括：人文历史，操作活动，专题学习.纵向拓展课程包括：学科拓展.人文历史等主要体现了数学的发展历程、数学家的探索精神，以及数学在实际生活中的广泛应用；操作活动主要体现了技术与数学的整合，运用技术解决数学问题，或者运用数学解释自然界中的现象；专题学习主要体现在对一个专题进行研究.

三、拓展性内容的教学设计

1.教材的背景分析

位于浙教版《义务教育教科书·数学》八年级下册第四章“平行四边形”的章尾，将四边形的学习延伸到置于网格中的多边形的面积探究.

2.教学目标设计

通过对网格中的多边形的面积的探究，让学生了解到网格中求多边形的面积不仅是数格子，还可以引进新思路——数点（包括边界上的点和内部的点）；整个探究过程主要运用了控制变量法（即单一变量法）以及函数模型法；培养学生的探究意识、探究精神和探究能力.

3.实际教学情境的铺设

第一环节：铺设情境，引出概念.

抛出图形，引出定义：如图1～3，一个多边形的各顶点都在格点上，这样的多边形叫做格点多边形.它的面积求法：可以统计多边形所围成的方格数或者割补法.

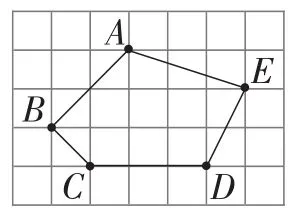
图1

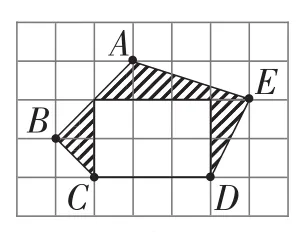
图2

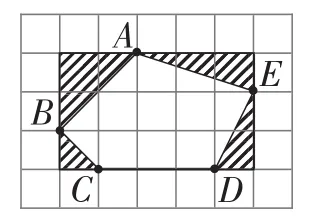
图3

第二环节：设计提问环节，挖出相关变量.

问题1：还有没有更简便的方法？

问题2：观察图4，分析格点多边形的面积大小与哪些量有关？

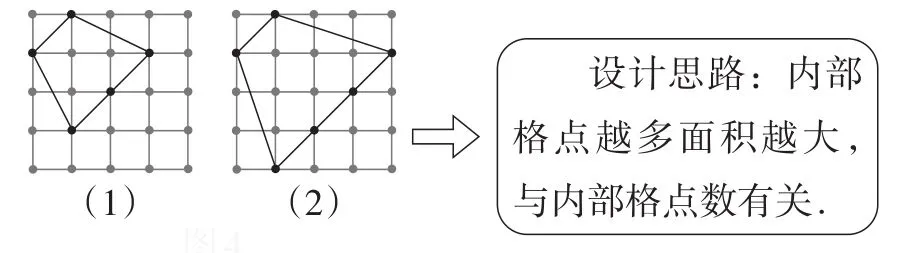
图4

问题3：如图5，当内部格点数相同时，为什么面积也会不同？

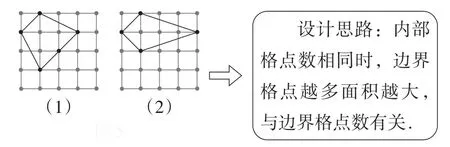
图5

得出结论：格点多边形的面积与内部格点数和边界格点数有关.

第三环节：控制变量，推出公式.

如图6，我们先研究凸多边形.

记格点多边形的面积为S，多边形内部的格点数为n（取“内”的首字母），它的边界的格点数为b（取“边”的首字母），那么S与n，b三者之间有怎样的数量关系呢？

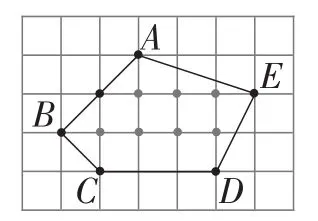
图6

教师做如下引导.

第一步：当n=3时，观察图7，数出这4个多边形边界上的格点数，并计算对应格点多边形的面积.

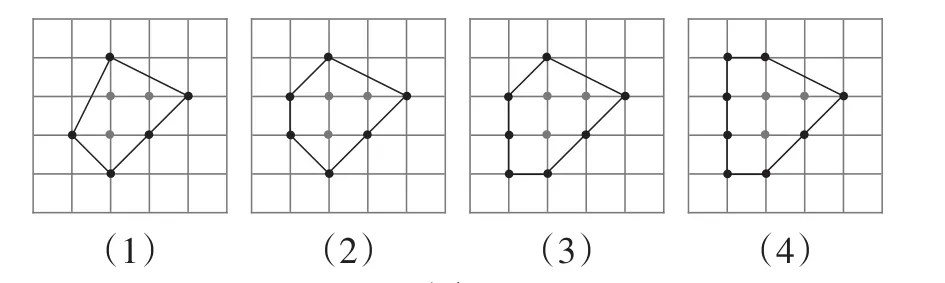
图7

第二步：填写下表.

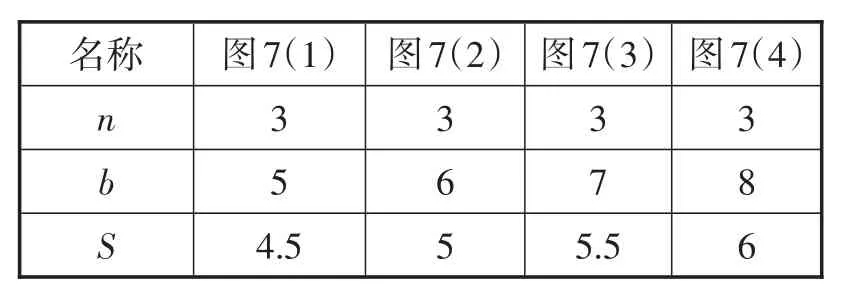
名称图7（1）图7（2）图7（3）图7（4）n b S 3 5 3 7 4.5 3 6 5 5.5 3 8 6

第三步：当n=3时，在直角坐标系中画出S关于b的函数图象，判断它是哪一类函数，并求出其函数表达式.具体操作如图8所示.

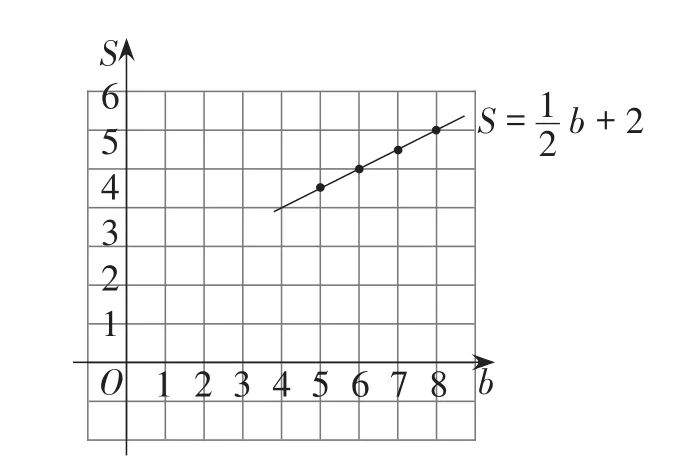
图8

由此可以得到：当n=3时，S与b的函数关系是

第四环节：分组合作，探究关系.

上面求出的函数表达式是当n=3时的情况，更一般地，当n取不同值时，S与b的函数关系又是如何呢？学生在已给出的学习单中进行研究，其中学习单上提供了方格纸、表格和直角坐标系.

合作要求：以小组为单位，探究n为某一固定值时，S与b满足的关系式；每位成员根据组长要求先算一个符合要求的图形面积，再组内交流合作，完成学习单；展示并交流成果.

预设学生答案：

（1）当n=1时，

（2）当n=2时，

（3）当n=3时，（已证）；

（4）当n=4时，

（5）当n=5时，

第五环节：根据规律，得出结论.

观察等式右边的一列数字与n的变化规律，由此发现S与n，b的关系

4.特殊到一般，发散思维研究

如图9，皮克定理是否适用于凹多边形？

皮克定理是否适合在矩形网格中研究？三角形网格呢？六边形网格呢？

图9

四、研究与建议

笔者整理得出拓展性课程的开展思路如图10所示.

1.拓展性课程开展的基本思路

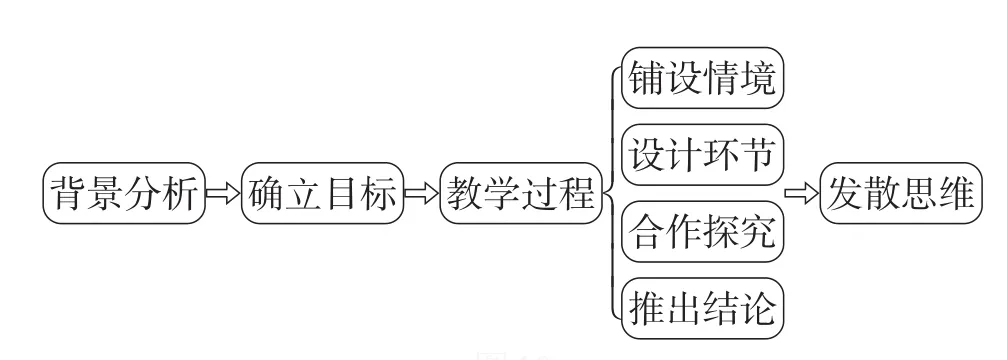
图10

2.对拓展性课程的教学建议

人文历史材料是教材知识的有机补充，同时也体现了十分重要的数学思想.例如，《神奇的π》中渗透了逼近与极限的数学思想，平时教材以及复习考试中都很少涉及，但我们可以从《神奇的π》中捕捉到这一重要的数学思想.在材料中提及了德国数学家莱布尼茨的证明

我们在教学中将这个公式稍加变形：

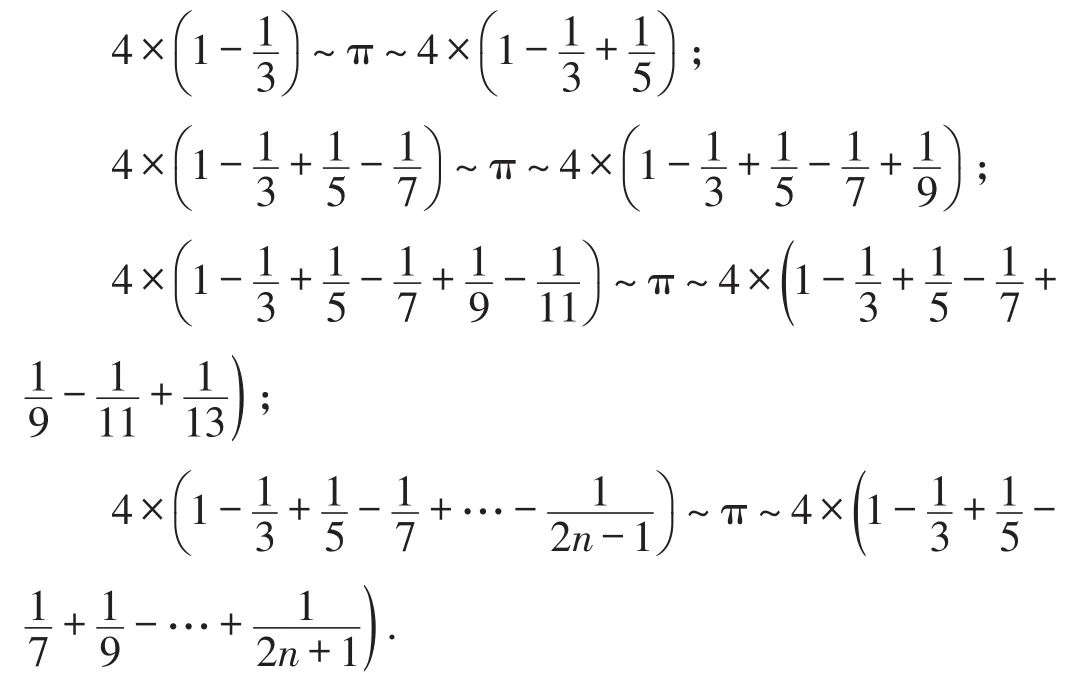
在课堂教学中教师可以引导学生运用上述方法得到一系列越来越接近于π的近似值，让学生经历这一过程，不仅可以培养他们探索与发现的能力，还可以使他们感受到用有理数逼近无理数这一重要的数学思想.

学科拓展、操作活动材料是一种有益的补充和延伸.例如，教材八年级上册阅读材料《从勾股定理到面积关系的拓展》，在教学中可以根据阅读材料的内容设计一些探究性的专题.

画一画：将三个正方形画成其他图形，使所画的分别以a，b，c为边的三个图形的面积仍满足S1+S2=S3.

验一验：分别以a，b，c为边所画的三个图形的面积满足S1+S2=S3，则所画的图形应满足什么条件？

三角形：如图11，a，b，c边上的高分别都是a，b，c的k倍，k＞0．

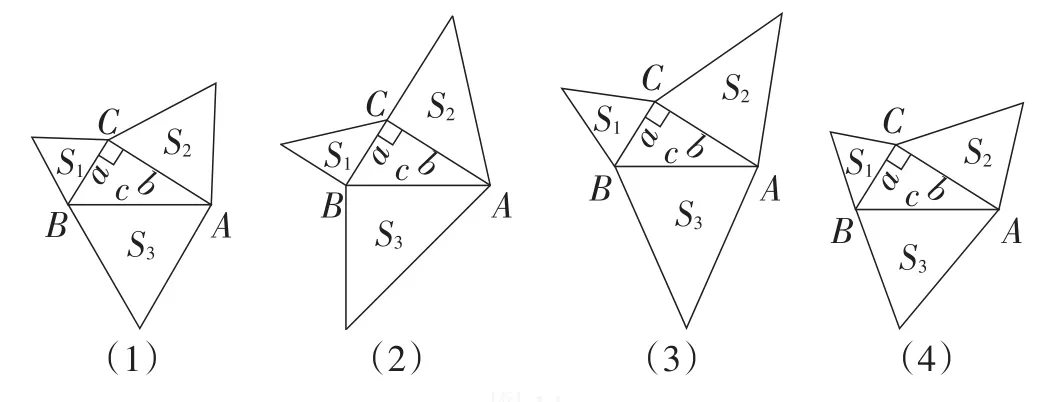
图11

平行四边形：如图12，a，b，c边上的高分别都是a，b，c的k倍，k＞0．

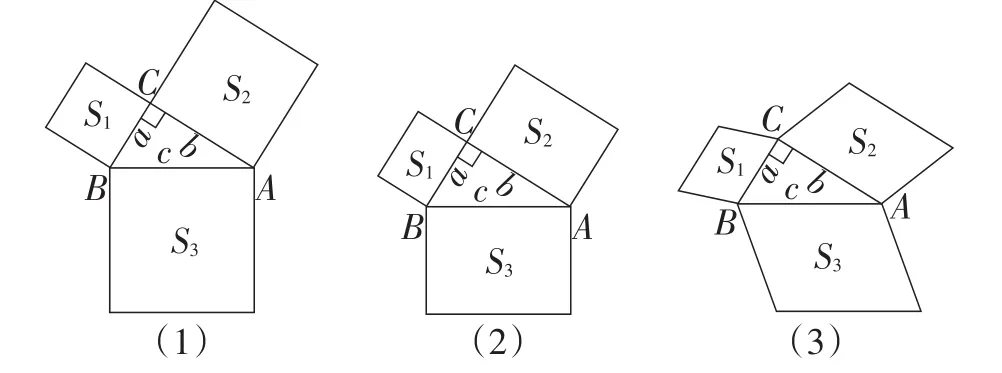
图12

梯形：如图13，另一底的长分别都是a，b，c的k倍，高也分别都是a，b，c的m倍，k＞0，m＞0．

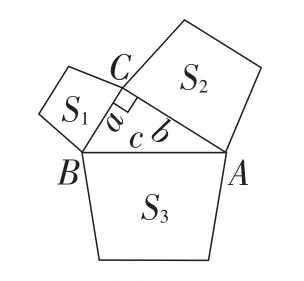
图13

这样的教学设计让学生经历了“分别以直角三角形两条直角边为边，向外所作的两个图形的面积之和S1+S2，等于以斜边为边向形外所作图形的面积S3”的形状和条件探索，发展了学生的合情推理和归纳总结能力.

拓展性课程的建设涉及原有课程的二次开发，最重要的体现是在备课上，它不是我们以往的备课，而是教师在课程意识的观念下，将课程资源转化为实践.所以说教材既是拓展性课程的“示范板”，也是教师的“实践板”.好的教师应当是双料专家——研究教材的“专科专家”和研究课程的“发展专家”.充分利用教材中的拓展性资源，让它大放光彩，开发适合的拓展性课程.我们也像学生一样，需要有充足的时间和空间，任重而道远.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］许芬英.浙江省中小学学科教学建议案例解读［M］.杭州：浙江教育出版社，2015.

2017—09—29

陆明（1982—），男，中学一级教师，主要从事中学数学教育教学研究.