基于效用最大化的投资组合模型
武可栋 韦增欣


[摘 要] 效用是投资者确定投资策略的一个很重要指标,由此有了效用最大化投资组合模型。本文根据均值-半方差模型对均值-方差模型修正的思想,建立了修正后的效用最大化投资组合模型。使用二次规划的一种求解方法——积极集法,对模型进行了求解。实证分析表明,修正后的模型可以为投资者提供有效的投资策略。
[关键词] 效用最大化;投资组合;积极集法
doi : 10 . 3969 / j . issn . 1673 - 0194 . 2017. 01. 069
[中图分类号] F830.59;F224 [文献标识码] A [文章编号] 1673 - 0194(2017)01- 0119- 04
1 前 言
在证券投资组合理论研究和具体实践中,马克维茨(Markowitz)证券投资组合均值-方差模型不仅是现代证券投资组合理论的基石,也是整个现代金融经济理论的基石。它不但使投资组合的研究在理论上得到飞跃,而且还在证券市场的应用上引起一场革新。直到今天,人们在处理证券投资组合的收益-风险分析时,Markowitz证券投资组合均值-方差模型仍然是一个基本工具。虽然Markowitz的均值-方差模型是最早用比较准确的数量关系来衡量风险的方法,但由于其严格的条件限制和复杂的计算,加上用方差来度量风险的自身局限性,使其在应用中受到很大的限制。
近几年来,学者们对均值-方差模型进行批评、改进的同时,也提出了其他的风险度量模型,主要分为三类:一类是以均值-方差模型为基础的,包括方差、标准差、绝对偏差等;另一类是非线性风险指标,主要以Hurst指数为代表;最后一类是以收益率下方为风险度量目标的,包括下偏矩(LPM)、VaR、半方差等。但由于各种模型自身的一些局限性,至今仍没有哪一种模型能够在学术界和投资界中占据主流地位。
投资者一般把预期收益率下方视为风险,而把预期收益率上方视为超额收益,均值-半方差模型作为均值-方差模型的改进,以收益率下方为风险度量因子,更符合投资者在现实中的真实心理感受。近几年随着计算机行业的发展,使得均值-半方差模型的求解速度得以提升,均值-半方差模型显示出了强大的生命力和应用价值,对投资者具有良好的现实指导意义。
然而,因为证券市场是典型的信息不对称市场,证券收益具有不确定性,投资者无法准确判定各风险证券的未来收益,所以追求自身效用的最大化是投资者的一个很好地选择。效用的判定作为投资者的主观决策行为,投资者不同则相应的效用函数不同。由于在完全竞争的证券市场中已知的效用函数和初始偏好可以完整地把个体的风险偏好、理性程度等进行刻画。所以,学者对效用的研究也逐渐深入,建立了效用最大化投资组合模型。效用最大化投资组合模型在现实中有着广泛的应用,在国内也有不少的研究成果。例如:屠新曙等,研究了含无风险资产时投资组合的效用最大化问题;张鹏等研究了效用最大化模型的有效前沿,并且对模型的求解算法也进行了探索;袁子甲等分析了参数不确定性以及投资者初始信念对最优投资策略的影响。
本文基于均值-半方差模型对均值-方差模型修正的思想,对效用最大化模型进行了改进,提出了用半方差修正的效用最大化模型。
6 结 语
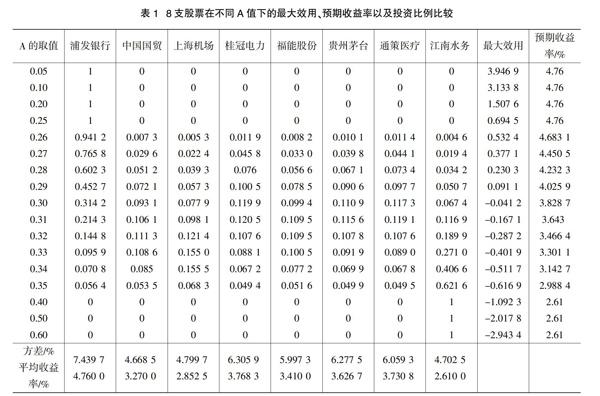
本文在效用最大化投资组合模型的基础上,对模型进行了优化,建立了新的效用函数,修正了原有的效用最大化投资组合模型,并针对模型的特点,采用积极集算法对模型进行求解。为验证模型的合理性和算法的有效性对选择的8支股票进行了实证分析。实证分析表明,该模型在定量分析中,与已有的基本结论一致,可以反映出风险与收益的关系,因此能够为投资者投资提供参考依据。
主要参考文献
[1]H Markowitz.Portfolio Selection[J].The Journal of Finance,1952,7(1): 77-91.
[2]卫海英,徐广伟. 半方差风险计量模型的实证比较及改进研究[J].暨南学报:哲学社会科学版,2004,26(5):24-30.
[3]屠新曙,王春峰,巴曙松.投资组合效用问题的研究[J].数量经济技术经济研究,2002,19(5):37-40.
[4]张鹏.基于参数法的效用最大化投资组合有效前沿研究[J].武汉科技大学学报,2013,36(1):74-80.
[5]袁子甲,李仲飞.参数不确定性和效用最大化下的动态投资组合选择[J].中国管理科学,2010,18(5):1-6.
[6]Ma,Yuhong,X Gong,and G Tian.A Mean-Semi-variance Portfolio Optimization Model with Full Transaction Costs[C]//2014 International Conference of IEEE on Computational Intelligence and Communiceation Networks,2014:623-627.
[7]Reny,Philip J.Advanced Microeconomic Theory[M]. Ottawa:Addison Wesley,1998.
[8]Neumann J L V,Morgenstern O V.The Theory of Games and Economic Behavior[M].Princeton,NJ:Princeton Universtiy Press,1945.
[9]赵长明. 我国二手房地产交易价格风险的核算[J]. 统计与决策, 2014(1):12-14.
[10]Schoemaker P J H.The Expected Utility Model:Its Variants, Purposes,Evidence and Limitations[J]. Journal of Economic Literature,1982,20(2):529-563.
[11]屠新曙.证券市场风险管理[M].北京:科学出版社,2008.
[12]Markowitz H M.Portfolio Selection:Efficient Diver-sification of Investments[M].New York:John Wiley,1959.
[13]徐绪松,马莉莉,陈彦斌.考虑损失规避的期望效用投资组合模型[J].中国管理科学,2007(5):42-47.
[14]解可新.最优化方法[M].天津:天津大学出版社,2004.
[15]刘兴高.应用最优化方法及Matlab实现[M].北京:科学出版社,2014.
[16]王继光.积极集法在天然气管网最大收益优化模型中的应用[C]//全国油气储运科技、信息与标准技术交流大会,2013.

