Hilbert空间中连续K-对偶的性质

侯美琴, 姚喜妍

(1.山西师范大学数学与计算机科学学院,山西 临汾 041000;2.运城学院应用数学系,山西 运城 044000)

Hilbert空间中连续K-对偶的性质

侯美琴1, 姚喜妍2

(1.山西师范大学数学与计算机科学学院,山西 临汾 041000;2.运城学院应用数学系,山西 运城 044000)

文章引入Hilbert空间连续K-对偶,连续K-对偶对的概念,应用算子论的方法,讨论了Hilbert空间H上连续K-对偶和连续K-对偶对的若干性质及稳定性,并对已有文献的相关结论进行了推广．

算子;连续K-对偶;连续K-对偶对;稳定性

1 引言

框架理论[1]是泛函分析、算子理论和非线性逼近等相结合的产物.随着框架理论的发展,各种框架概念被提出,如:fusion框架[2],g-框架[3],K-框架[4-5],控制框架[6]等.

K-框架是由Gavruta在研究有界线性算子K的原子分解系统时引入的.诸多研究者对K-框架进行了详细研究[7-9],并引入了K-fusion框架[10-11]和连续K-框架[12-13]概念.与一般框架相比,K-框架可在值域R(K)中重构Hilbert空间中的元素.但对于框架的很多性质而言,K-框架就不一定成立了.而连续K-框架比K-框架更具有一般性,因此在K-框架上成立的相关性质在连续K-框架上也不一定成立.目前,一些学者对连续K-框架的研究甚少,所以有必要对连续K-框架进行更加深入的研究.文献[11]给出连续K-框架的多种等价条件,连续K-框架交错对偶的充分条件,和构造新连续K-框架的方法.文献[9-13]对Hilbert空间中连续K-框架的两种等价进行了刻画,并讨论了连续K-框架的扰动和冗余性.本文主要在文献[9]的基础上,将Hilbert空间上K-框架的若干性质推广到连续K-框架上,给出了连续K-对偶,连续K-对偶对的概念.应用泛函分析和算子论的方法,讨论了连续K-对偶和连续K-对偶对的若干性质及稳定性,得出一些有意义的结果.

2 预备知识

为了方便起见,先给出本文中要用到的记号,H表示无限维可分 Hilbert空间;(Ω,Σ,µ)或 (Ω,µ)表示一个σ−有限,正可测空间;N表示指标集;B(H1,H2)表示从 Hilbert空间H1到 Hilbert空间H2上的有界线性算子全体所组成的集合,若H1=H2=H,则记B(H1,H2)=B(H);C表示复数域;R(T),NT分别表示有界算子T的值域和核;I为H上的恒等算子;T+表示算子T的伪逆算子;T∗指算子T的伴随算子;BH表示全体Bessel集所组成的集合;Fk(H)表示H上全体连续K-框架所组成的集合．

定义2.1[5]设K∈B(H),序列{fi}i∈N称为H的K-框架,若存在常数0＜A≤B＜∞,使得

A,B分别称为框架{fi}i∈N⊆H的下界,上界．如果只有右不等式成立,则称{fi}i∈N为K-Bessel列,Bessel界为B.特别地,如果

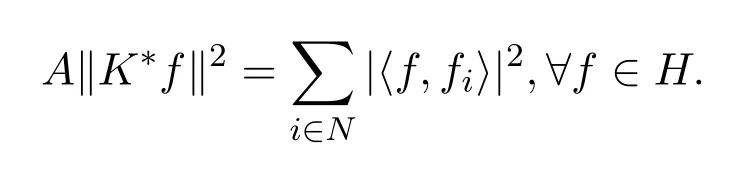
则称{fi}i∈N为H的紧K-框架．若在上面等式中A=1,则称相应的紧K-框架{fi}i∈N为的ParsevalK-框架．如果算子K是零算子,则称K-框架为零-框架．

注 2.1由框架与K-框架的定义知,若K=I,则H的K-框架就是H的框架．因此K-框架被视为框架的一种推广.但是框架中的一些结果在K-框架中是不成立的,文章在此不讨论这方面内容,详见文献[4-5,7-9].

定义 2.2[5]设K∈B(H),h={hm∈H:m∈Ω}为H中的一族元素,若满足：

(2)存在0＜A≤B＜∞,使得

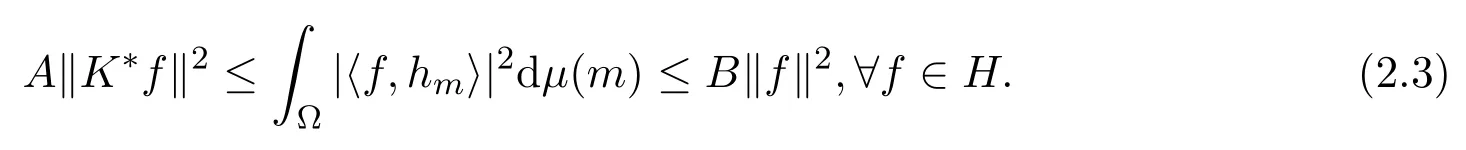
则称h={hm∈H:m∈Ω}为H关于(Ω,µ)的连续K-框架．简称h为H上的连续K-框架.A,B分别称为连续K-框架的下界和上界．若

则称h为H上的连续紧K-框架:若A=1,则称h为H上的连续ParsevalK-框架.若定义2.2中(2)的右不等式成立,则h被称为Bessel集,称B为Bessel界．

注 2.2(1)当K=I时,连续K-框架为连续框架或称为广义框架;

(2)当Ω=N,µ是计数测度时,连续K-框架为(离散)K-框架.

定义 2.3[9]设有界可逆算子T∈B(H1,H2),若TK1T∗=K2,则称K1与K2关于算子T相似等价.其中K1∈H1,K2∈H2．特别地,若T是酉算子,则称K1与K2酉等价.

引理 2.1[14]设H1,H2是可分的Hilbert空间,U∈B(H1,H2)是闭值域算子．则存在唯一的U+∈B(H2,H1)使得

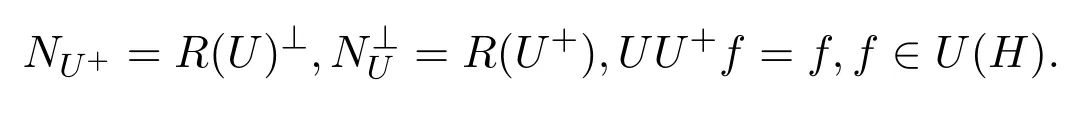
定理 2.1[14]设H1,H2是可分的Hilbert空间,U∈B(H1,H2)是闭值域算子.则

(1)UU+是H1到R(U)上的正交投影算子;

(2)U+U是H2到R(U+)=R(U∗)=N⊥U上的正交投影算子;

(3)‖U∗f‖≥‖U+‖‖f‖.

3 主要结论

定理 3.1设K∈B(H),h∈FK(H),框架界为A,B．则Kh是H上的连续K2-框架,即Kh∈FK2(H),且框架界为A,B‖K‖2．

证明根据定义2.2知,∀f∈H,h满足(2.3)式,且,∀f∈H,有

所以Kh∈FK2(H)是H上的连续K2−框架,且框架界为A,B‖K‖2．

定理 3.2设h∈FK(H),框架界为A,B．则Kαh是H的连续Kα+1−框架,即Kαh∈FKα+1(H),且框架界为A,B‖K‖α+1．其中α∈R(证明过程与定理 3.1类似,这里省略).

定义 3.1设K∈B(H),h∈FK(H),k∈BH,若满足

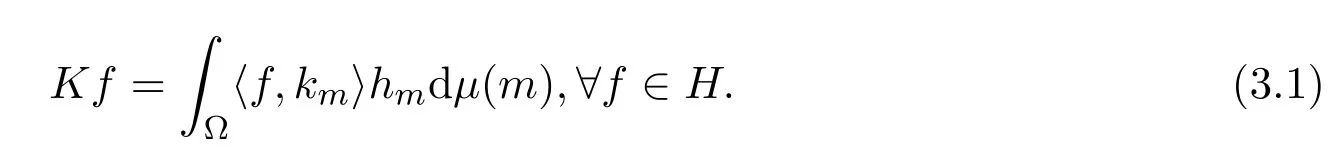
则称k为h的连续K-对偶．

定理 3.3设h,k∈BH,若

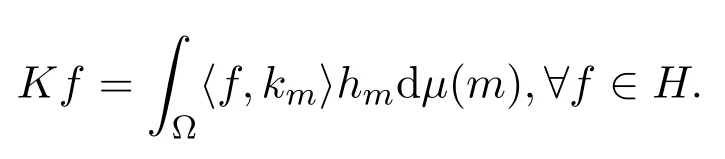
则

进而h={hm∈H:m∈Ω}为H上的连续K-框架,k={km∈H:m∈Ω}为H上的连续K∗-框架.

证明∀f∈H,有

其中M为k的Bessel界.从而

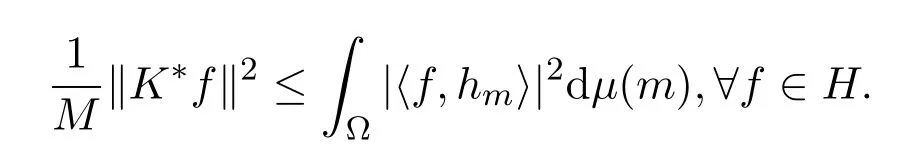
又h为H上的 Bessel集,所以h={hm∈H:m∈Ω}为H上的连续K-框架.同理k={km∈H:m∈Ω}为H上的连续K∗−框架,即h∈FK(H),k∈FK∗(H).

另外,对∀f,g∈H,有

则

定义 3.1如果上述定理3.3条件不变且满足(3.1)和(3.1)两式的h,k称为H上的连续K-对偶对,记为(h,k)．进一步k为h的连续K-对偶,h为k的连续K∗-对偶．

注 3.1当K是自伴算子时,k为h的连续K-对偶,h为k的连续K-对偶.即(k,h)也为H上的连续K-对偶对．

注 3.2由定理3.3易得K-对偶与框架的交错对偶具有相似的对称性,但不像交错对偶那样具有交换性．当在子空间R(K)上时可实现交换性,且有如下定理：

定理 3.5设K∈B(H),R(K)是闭的,(h,k)为H上的连续K-对偶对,则有

同样

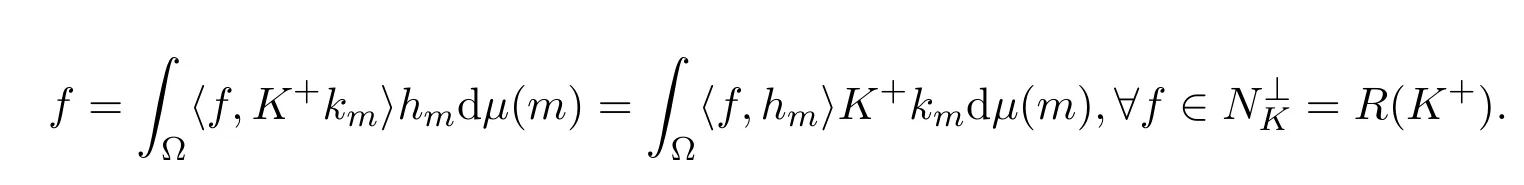
证明由引理2.1知,KK+f=f,∀f∈R(K),且由定义 3.1得

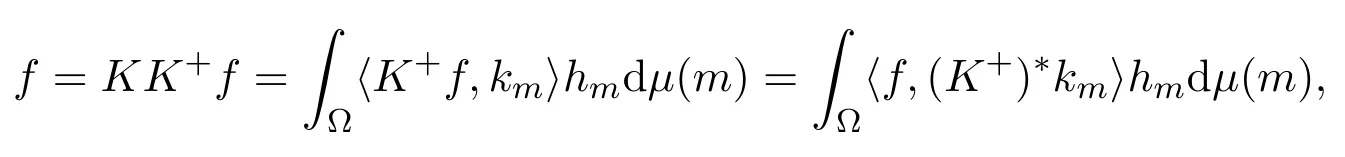
于是

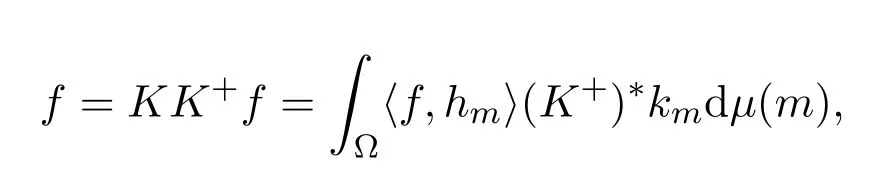
所以

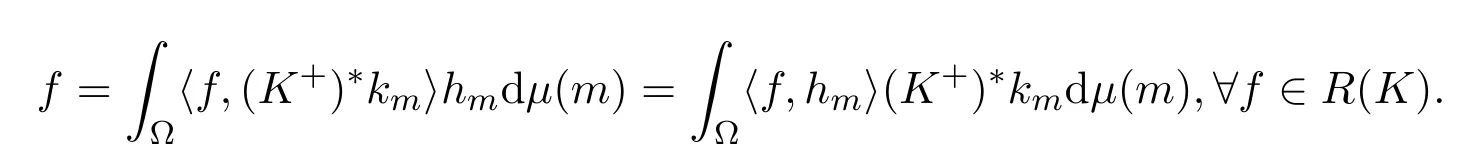
另外,

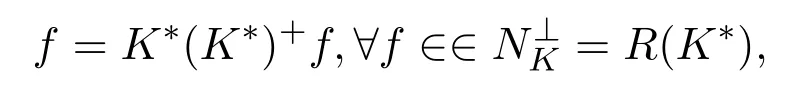
且由定义3.2得

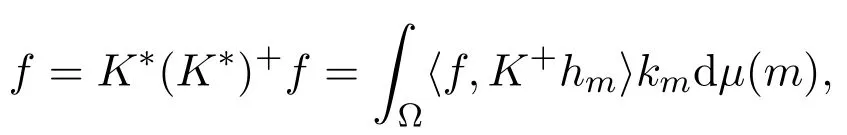
从而

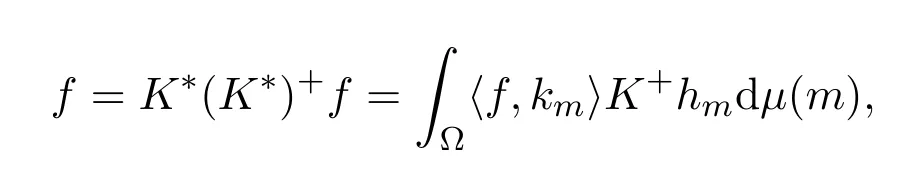
因此

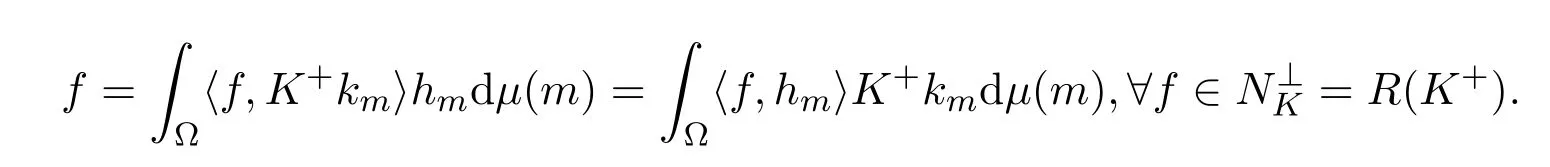
定理3.6设h∈BH,K∈B(H),R(K)是闭的,P:H→R(K)是正交投影,则h∈FK(H)当且仅当{Phm}m∈Ω为R(K)上的连续框架．

证明若h∈FK(H),则存在0＜A≤B＜∞,使得(2.3)成立．且由定理2.1,∀f∈R(K)有

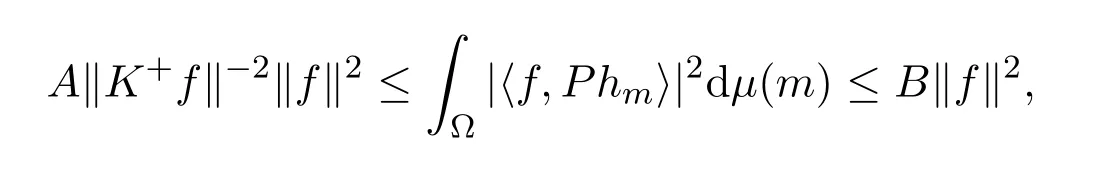
所以{Phm}m∈Ω为R(K)上的连续框架．

若{Phm}m∈Ω为R(K)上的连续框架,其框架界A,B,T为合成算子,则R(K)=R(T).从而由文献 [9]的引理 2.2有KK∗≤λ2TT∗(其中).设

这样有

成立,所由定义 2.2得h∈FK(H)．

定理 3.7设K∈B(H),R(K)是闭的,h∈FK(H),其框架算子S的值域是闭的,P:H→R(K)是正交投影,则是{Phm}m∈Ω的连续K-对偶,其中SP为{Phm}m∈Ω的框架算子．

证明由定理3.5知{Phm}m∈Ω为R(K)上的连续框架,这样{Phm}m∈Ω为R(K)上的连续K-框架.于是由连续框架算子的性质知,∀f∈R(K)有

从而

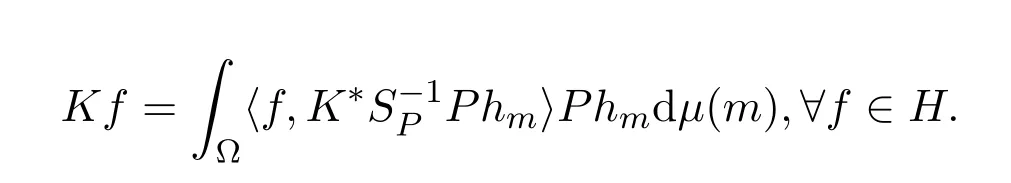
定理 3.8设f∈R(K),R(K)是闭的,h∈FK(H)框架界为A,B,若k为h的连续K-对偶,则Kk是H上的连续K-框架．

证明由定义3.1和定理3.3知k∈FK∗(H)所以存在0＜A≤B＜∞,使得

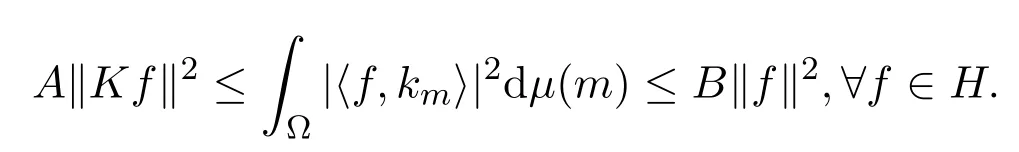
从而

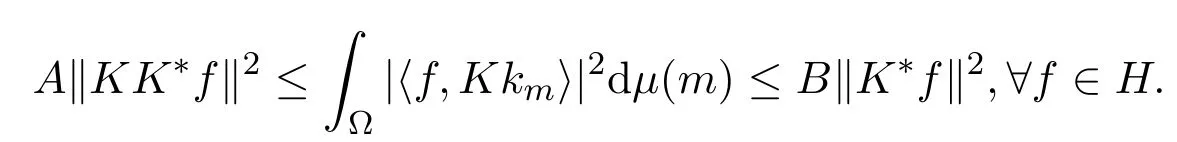
令g=K∗f,g∈R(K∗)=N⊥K,又R(K)是闭的,所以根据引理2.1,有g=K+Kg,∀g∈R(K∗),从而

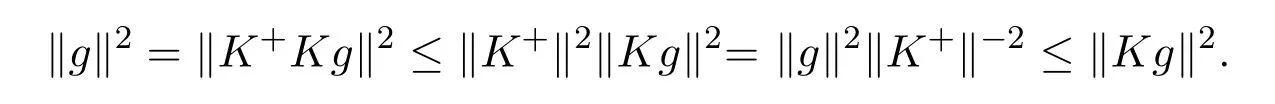
综上所述得

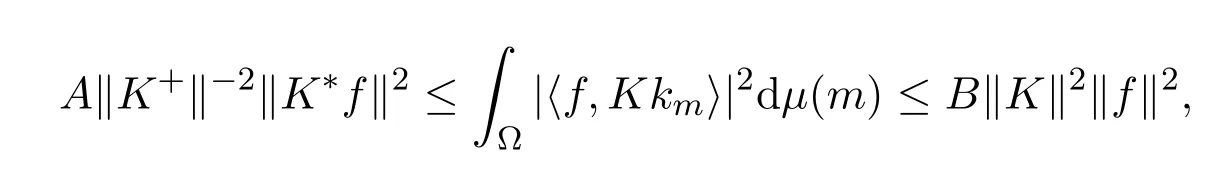
所以Kk是连续K-框架,且框架界为A‖K+‖−2,B‖K‖2.

定理 3.9设K1,K2∈B(H)是闭值域算子,且K1,K2关于可逆算子T相似等价,若(h,k)为H上的连续K1-对偶对,则(Th,Tk)为H上的连续K2-对偶对.

证明根据定义3.1,有

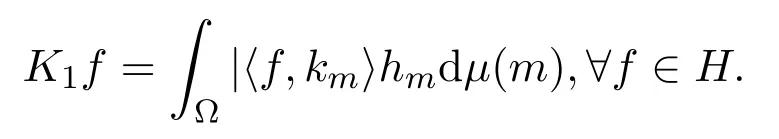
再由定义 2.3知TK1T∗=K2,从而∀f∈H,有

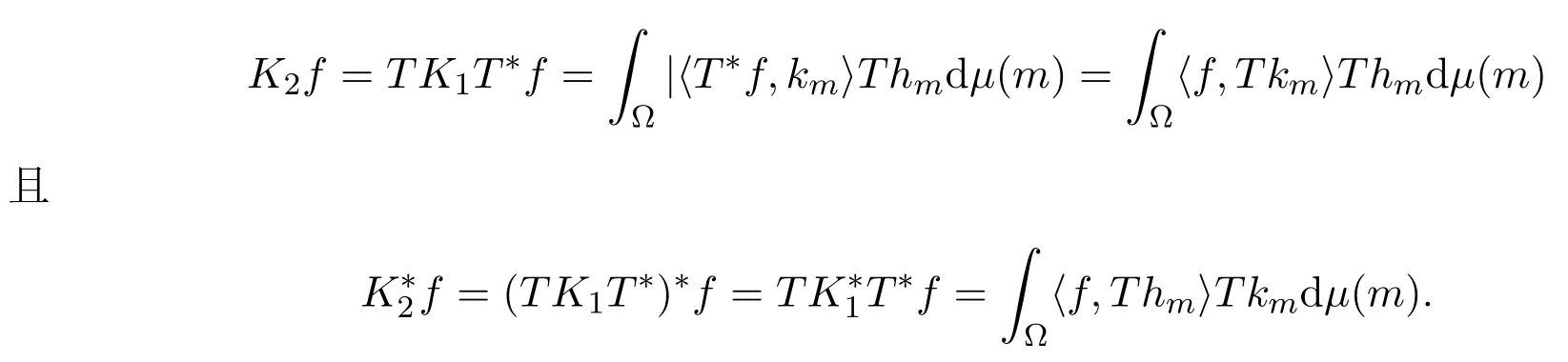
所以根据定义3.1和定理3.3知(Th,Tk)为H上的连续K2-对偶对.

定理 3.10设K∈B(H),若(h,k)为H上的连续K-对偶对,则(Kh,k)为H上的连续K2-对偶对．

证明由定义3.2和定理3.3知f∈H,

从而

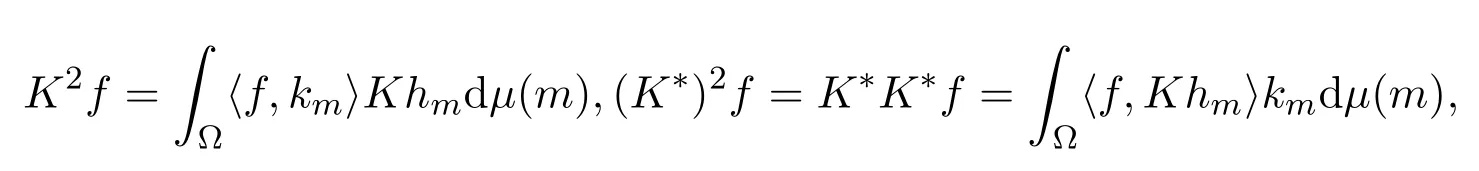
所以由定理3.3和定义3.2得(Kh,k)为H上的连续K2对偶对.

定理 3.11设K∈B(H)且自伴,若(h,k)为H上的连续K-对偶对,则(h,Kk)为H上的连续K2−对偶对(证明过程与定理3.9类似).

定理 3.12设K∈B(H),若 (h,k)为H上的连续K-对偶对,则(Kαh,k)为上的连续Kα+1对偶对．其中α∈R(证明方法与定理3.9类似,故略).

注 3.1当K=I时,上述定理3.8-定理3.11在连续框架和(离散)K-框架上仍成立．

定理 3.13设K∈B(H),T∈B(H),若(h,k)为H上的连续K-对偶对,则(Th,k)为H上的连续TK-对偶对.

证明由定义3.1知,∀f∈H,

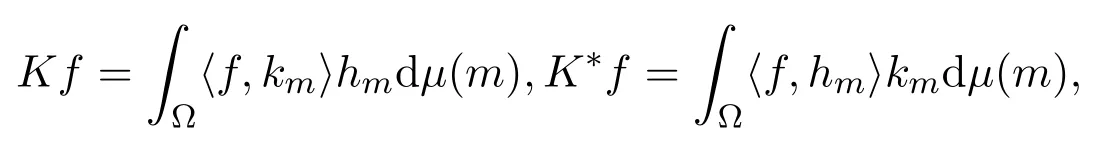
从而有

因此由定理3.3和定义3.1得(Th,k)为H上的连续TK-对偶对．

定理 3.14设K,T∈B(H),T,K自伴且TK=KT,若(h,k)为H上的连续K-对偶对,则 (Th,k),(Tk,h),(k,Th),(h,Tk)为H上的连续TK-(KT−)对偶对．即Th与k可交换,同时h与Tk也可交换.

证明由定义3.3知,∀f∈H,

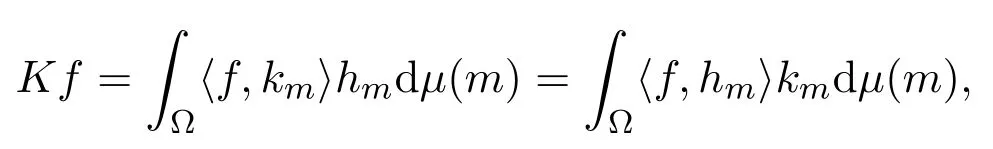
从而有

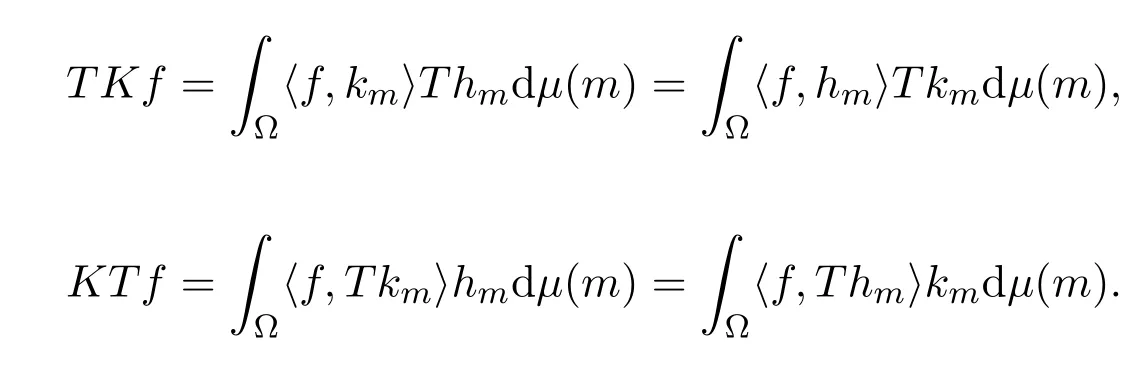
又TK=KT,因此 (Th,k),(Tk,h),(k,Th),(h,Tk)为H上的连续TK-(KT−)对偶对．即Th与k可交换,同时h与Tk也可交换.

定理 3.15设K,T∈B(H)是酉算子,且TK=KT,若k为h的连续K-对偶,则Tk为Th的连续K-对偶.

证明由定义3.1和酉算子的性质知,∀f∈H,

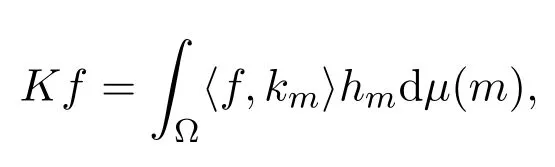
从而有

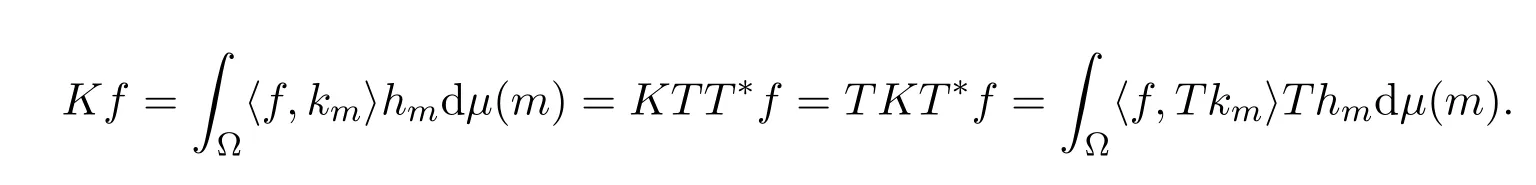
因此Tk为Th的连续K-对偶.

致谢衷心感谢导师姚喜妍教授的悉心指导．

[1]Duffin R J,Schaeffer A C.A class of nonharmonic courier series[J].Trans.Amer.Math.Soc.,1952,72(3):341-366.

[2]Casazza P G,Kutyniok G.Finite frames and distributed processing[J].Appl.Comput.Harmon.Anal.,2008,25:114-132.

[3]Sun W.G-frames and g-Riesz bases[J].J.Math.Anal.Appl.,2006,322(1):437-452.

[4]Gavruta L.Frames for operators[J].Appl.Comp.Harm.Anal.,2012,32:139-144.

[5]Gavruta L.New results on frames for operators[J].Proc.Intern.Conf.Sciences,2012(2):55-61.

[6]Balazs P,Antoine J P.Weighted and controlled frames[J].Int.J.Wavelets MultiresolutInf Process,2010,8(1):109-132.

[7]Xiao X C,Zhu Y C.Laura gavruta some properties ofK-frames in Hilbert spaces[J].Results.Math.,2013,63:1243-1255.

[8]丁明玲,肖祥春,朱玉灿.Hilbert空间中的K-框架[J].数学学报,2014,57(6):1089-1100.

[9]李亮,李鹏同.Hilbert空间上的K-框架与K-对偶[J].南京大学学报数学:半年刊,2015,32(1):74-88.

[10]周燕.K-fusion框架的刻画[J].福建师范大学学报:自然科学版,2013,29(2):11-15.

[11]周燕.K-fusion框架扰动的稳定性[J].数学杂志,2013,33(2):322-328.

[12]肖祥春,丁明玲,朱玉灿.Hilbert空间连续K-框架的若干研究[J].安徽大学学报:自然科学版,2013,37(2):31-35.

[13]范丽兰,舒志彪.Hilbert空间连续K-框架的冗余与扰动性[J].福州大学学报:自然科学版,2016,44(1):6-11.

[14]Christensen O.Frames and pseudo-inverses[J].Appl.Comput.Harmon.Anal.,1995,195:401-414.

The properties of continuousK-dual in Hilbert spaces

Hou Meiqin1,Yao Xiyan2
(1.College of Mathematics and Computer Science,Shanxi Normal University,Linfen 041000,China;2.Department of Applied Mathematics,Yuncheng University,Yuncheng 044000,China)

In this paper,we introduce the concepts of continuousK-dual,a pair of continuousK-dual in Hilbert spaces.By using the operator theory,some properties and stability of the continuousK-dual,a pair of continuousK-dual frame in Hilbert spaces are discussed,and the related conclusions of the existing literatures be generalized.

operator,ContinuousK-dual,a pair of continuousK-dual,stability

2010 MSC:42C99,46C05,46C99

O177.5

A

1008-5513(2017)06-0652-09

10.3969/j.issn.1008-5513.2017.06.011

2017-11-08.

山西省自然科学基金(20130111003-1);山西省高校重点学科建设专项资金(20131010).

侯美琴(1989-),硕士生,研究方向：算子理论与小波分析.