带蝴蝶型耗能钢板的自复位结构体系的抗震和复位性能分析
诸文宽,李启才,黄自尊,程佳明
(苏州科技大学 土木工程学院,江苏 苏州215011)
带蝴蝶型耗能钢板的自复位结构体系的抗震和复位性能分析
诸文宽,李启才,黄自尊,程佳明
(苏州科技大学 土木工程学院,江苏 苏州215011)
带蝴蝶型耗能钢板的自复位结构体系是一种结合了耗能钢板耗能能力和自复位节点复位能力的新型抗震结构体系。文章提出其简化模型,给出建模方法,选取试验模型进行模拟验证。使用简化模型进行结构建模,通过静力非线性分析方法对结构进行循环往复加载。结果表明,结构体系滞回曲线呈现典型的“双旗帜型”,且较为饱满。通过计算结构能量耗散系数及层间残余位移角,表明结构抗侧能力较高,耗能能力较好,满足自复位结构体系性能设计要求。与有限元实体模型相比,简化模型建模方便,应用广泛。对结构体系进行参数分析,表明耗能钢板与钢绞线存在相互制衡的关系,需要相互匹配,才能使结构体系发挥较优性能。
蝴蝶型耗能钢板;自复位结构体系;静力非线性分析;滞回曲线;Opensees
地震灾害不仅对生命安全构成威胁,也常常导致建筑物出现较大损害且不可修复。对重要建筑物来说,震后无法修复会导致很大的经济损失。有鉴于此,一些学者提出了自复位结构体系的概念,这类结构体系在震后残余变形小,具有复位能力。
利用钢板剪力墙耗能的自复位结构体系有较好的抗震和复位性能。该结构体系利用预应力钢绞线将梁柱压紧,使节点具备足够的抗弯刚度,同时预应力钢绞线提供结构回复力。在地震中依靠钢板剪力墙进入塑性耗能,梁柱主要构件保持弹性,震后仅需更换钢板剪力墙。蝴蝶型耗能钢板是钢板剪力墙的改进形式之一,由开竖缝钢板剪力墙演化而来,整块钢板分割成一系列蝴蝶型短柱,短柱通过弯曲耗能,以此提高延性和耗能能力。
对于带蝴蝶型耗能钢板的自复位结构,目前的研究较少,研究以单层结构为主,采用有限元实体单元进行建模分析,分析复杂且耗时较多,不利于多层结构体系的分析及设计。有鉴于此,文中提出了带蝴蝶型耗能钢板的自复位结构体系的简化模型,并根据简化模型进行多层结构体系抗震和复位性能的研究。
1 有限元模型
带蝴蝶型耗能钢板的自复位结构几何模型(取一层)如图1所示。模型主要由自复位框架和内嵌耗能钢板构成,梁柱节点采用自复位节点,通过预应力钢绞线将梁柱压紧,梁柱脱开后节点起到复位作用。钢板采用两边连接,即钢板通过高强螺栓与框架梁连接,以此减少对框架柱的附加弯矩,符合强柱弱梁的抗震理念。
采用Opensees软件建模,建模所用的梁柱材料采用steel02材料,本构关系为理想弹塑性强化模型。设计模型中梁柱材料屈服强度Fy=345 MPa,弹性模量E=206 000 MPa,强化段切线模量Et=0.01E。梁柱单元采用nonlinear Beam Column单元,即非线性梁柱单元,该单元可应用于杆系单元的静力及动力非线性分析,且考虑结构效应。钢绞线材料也采用steel02材料,在steel02材料的基础上设置初始预应力值,材料屈服强度取为Fy=1 675 MPa,弹性模量E=196 000 MPa,强化段切线模量Et=0.01E,单元采用truss单元,以上材料和单元通过与试验验证,能较好地模拟自复位结构的性能。
文中的梁柱节点连接采用自复位节点连接(非固接也非铰接),为了合理地模拟出自复位节点,采用如图2所示的建模方式。只压弹簧位于梁端翼缘处,在梁柱脱开时便于梁柱缝隙的展开;斜向弹簧和只压弹簧相连,在梁柱缝隙展开时便于传递剪力。只压弹簧和斜向弹簧均采用corotTruss单元,单元材料为ENT,材料的弹性模量E=206 000 MPa。梁和柱位于同一平面内,且梁垂直于柱。
采用蝴蝶型耗能钢板,其充分利用了蝴蝶杆的弯曲屈服进行耗能。蝴蝶杆屈服所形成的塑性铰远离端部,使蝴蝶杆延性得以提升,典型的蝴蝶型耗能钢板如图3所示。根据Ma Xiang[1]的研究,蝴蝶型耗能钢板设计承载力和等效刚度分别如下

式中,E为蝴蝶型钢板弹性模量;Kc为钢板等效刚度;a为钢板连接中部宽度,取值为b/3;b为钢板连接根部宽度;t为钢板厚度;L为钢板连接长度;c为钢板连接区域宽度;nL为钢板连接个数;σy为钢板屈服强度。
[2],设计出如图4所示的蝴蝶型耗能钢板简化模型。主要分三个部分:两端刚性单元,中间部分组合单元以及转动弹簧单元(用来连接刚性单元与组合单元)。其中刚性单元采用elastic Beam Column单元,赋予较大的初始刚度,令其不产生塑性变形。组合单元由轴向单元 (disp Beam Column)和梁柱单元(nonlinear Beam Column)组成。轴向单元传递沿杆长方向的力,而梁柱单元传递垂直于杆长方向的力以及弯矩。轴向单元采用ElasticPP和Elastic材料,梁柱单元采用Steel01及Elastic材料,相关材料参数通过模拟试验校正及选取。转动弹簧单元采用零长单元(zero Length),用来模拟蝴蝶杆屈服所形成的塑性铰。耗能钢板发生塑性变形时转动弹簧开始转动,进行塑性耗能。转动弹簧单元的极限弯矩Mp及转动刚度KM的计算公式如下[3]

式中,Le为轴向单元的等效长度,取 Le=(3/4)L。
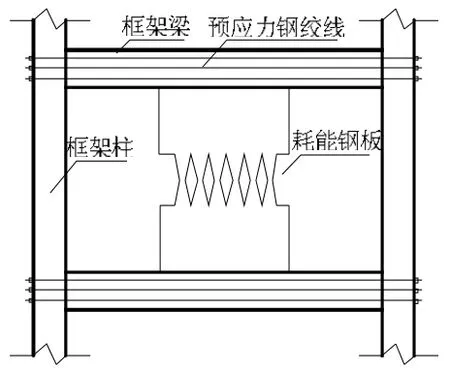
图1 带蝴蝶型耗能钢板的自复位结构简图

图2 自复位节点简图
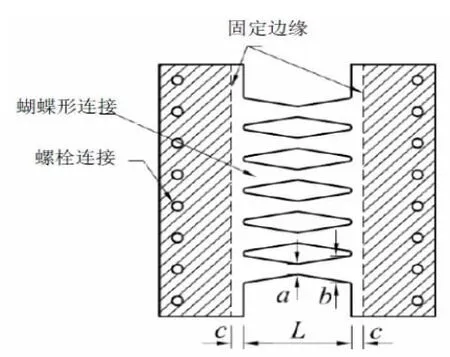
图3 典型的蝴蝶型耗能钢板

图4 简化模型图
2 模拟方法验证
为了验证自复位节点,以及蝴蝶型耗能钢板模型的合理性,选取如下试验进行模拟验证。
2.1 自复位节点的验证
对潘振华[4]等所做自复位节点试验进行模拟验证,来证明Opensees软件模拟自复位节点的可行性。选取JD3试件模拟,模拟简图如图5所示。梁长取3.8 m,柱子长度为3 m。梁、柱的截面分别为HN500×300×14×28和HW500×500×20×20。4根直径15.2 mm的钢绞线对称布置在腹板两侧;角钢采用焊接等边角钢L200×16,长度200 mm,和梁柱翼缘栓接。

图5 JD3有限元模型模拟图
梁柱,钢绞线材料的本构关系采用试验实测值。梁柱材料取Q345B,Fy=345 MPa。弹性模量E=206 000 MPa;角钢材料屈服强度为440 MPa,抗拉强度取为575 MPa,弹性模量取为E=200 000 MPa,强化段的弹性模量为0.01E;钢绞线的屈服应力取为1 860 MPa,弹性模量E=195 000 MPa。模拟方法如上文所述,其中角钢建模采用崔强[5]的模拟方法。
加载方式和试验一致,加载节点处的截面力-位移曲线,如图6所示。最初节点性能和焊接节点相似,有较大抗侧刚度。随着施加荷载加大,梁柱脱开,此时梁内剪力为44.2 kN。当剪力超过44.2 kN后,曲线斜率减小,节点刚度开始下降。节点脱开后钢绞线提供预拉力使结构复位。模拟处于比较理想的情况,相比试验忽略了一些缺陷,所以复位效果理想,残余变形较试验更小。如果进行预应力束拉力与水平推力关系图的比较(见图7),可以看出模拟曲线与试验曲线相接近,模拟效果较好。试验图中,结构经过多次往复加载后,钢绞线预拉力下降,可能是试验中钢绞线产生预应力损失,而模拟过程则处于较为理想的情况。
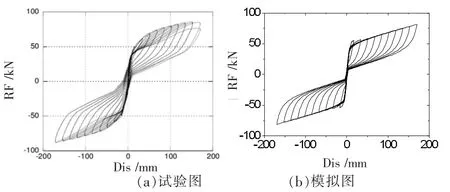
图6 顶点水平力-位移滞回曲线对比图

图7 预应力束拉力-水平推力关系图对比
2.2 蝴蝶型耗能钢板的验证
为了验证蝴蝶型耗能钢板简化模型的可行性,对Eatherton论文[3]中的A2号试件进行模拟。结构模型和简化模型分别为图8和图9所示。

图8 双跨可控摇摆自复位结构模型

图9 模型简图
A2模型中采用的蝴蝶型钢板尺寸为t=15.9 mm,L=356 mm,b=58.7 mm,nL=20,Ffusep=424.8 kN。从图10可以看出,在静力往复加载作用的下,结构的响应曲线和试验所得结果吻合较好。通过记录蝴蝶型耗能钢板中梁柱单元中的剪力,绘制出蝴蝶型耗能钢板的滞回曲线,如图11所示,可以看出,模拟结果与试验结果相接近。

图10 结构体系滞回性能验证对比

图11 蝴蝶型耗能钢板滞回性能验证对比图
3 有限元模型分析
3.1 模型尺寸及参数选取
利用有限元软件Opensees建立三层带蝴蝶型耗能钢板的自复位结构体系简化模型,建模方法参考上文。设计模型取自文献[6]中一个三层三跨的钢结构建筑,每层层高为3.3 m。抗震设防烈度为8度,基本加速度为0.3g,设计地震分组为一组,场地类别为二类。选取其中间跨,跨度为5.7 m,将其改造成带蝴蝶型耗能钢板的自复位结构,结构模型简图如图12所示,材料参数如前文所述,简化模型如图13所示。
通过建立BASE模型,分析该类结构体系的抗震和复位性能。设计是一个不断迭代的过程,文中参考了文献[7]~[9],通过计算水平地震力、梁柱校核、设计耗能钢板及钢绞线,不断迭代优化,最终选定的BASE模型梁柱参数如表1所示。模型中耗能钢板尺寸选取:b=60 mm,a=20 mm,t=20 mm,L=400 mm,c=25 mm,nL=22,耗能钢板宽度为1 500 mm。计算得到耗能器屈服承载力Ffusep为413.6 kN,等效刚度Kc为106.48 kN/mm。钢绞线每层布置数量和规格相同,沿每层梁中线对称布置,上下各布置1束,每束含7根钢绞线;每根钢绞线的初始预拉力为200 kN。
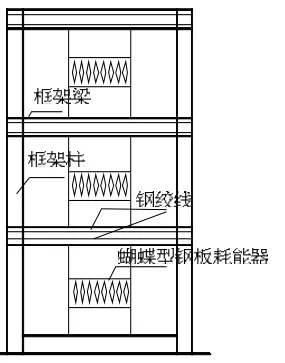
图12 模型简图
图13 简化模型图

表1 Base模型结构梁柱参数
3.2 静力非线性分析
结构在中震和大震作用下一般情况下会进入弹塑性状态。静力非线性分析,可有效地估计结构的非线性变形,相对于非线性时程分析获得更加稳定的分析结果。采用倒三角侧向力分布模式[10],按位移加载方式单调加载至结构层间位移角的4%,图14为倒三角加载模式下BASE模型的基底剪力-层间位移曲线。
从图14中看出,带蝴蝶型耗能钢板的自复位结构体系的荷载-位移曲线可简化为“双折线”模型,第一阶段为弹性阶段,此阶段结构由蝴蝶型耗能钢板和框架梁柱共同抵抗侧向力;第二阶段为弹塑性阶段,此时耗能钢板通过屈服耗能,而增加的抗侧力由钢绞线提供。经过验算,结构体系的抗侧能力可以满足抗震要求。
地震中结构受到往复振动且研究的结构体系具有自复位性能,通过分析往复荷载下结构体系的滞回曲线,更好地考察结构的抗震和复位性能。采用倒三角加载模式对结构进行往复荷载下的性能分析,按位移加载的方式往复推至结构体系层间位移角的4%。提取相关数据,图15为BASE结构的滞回曲线图,图16和图17分别为各层钢绞线拉力值及耗能钢板剪力值与各层层间位移角间的关系图。

图14 基底剪力-层间位移曲线

图15 BASE结构体系的滞回曲线
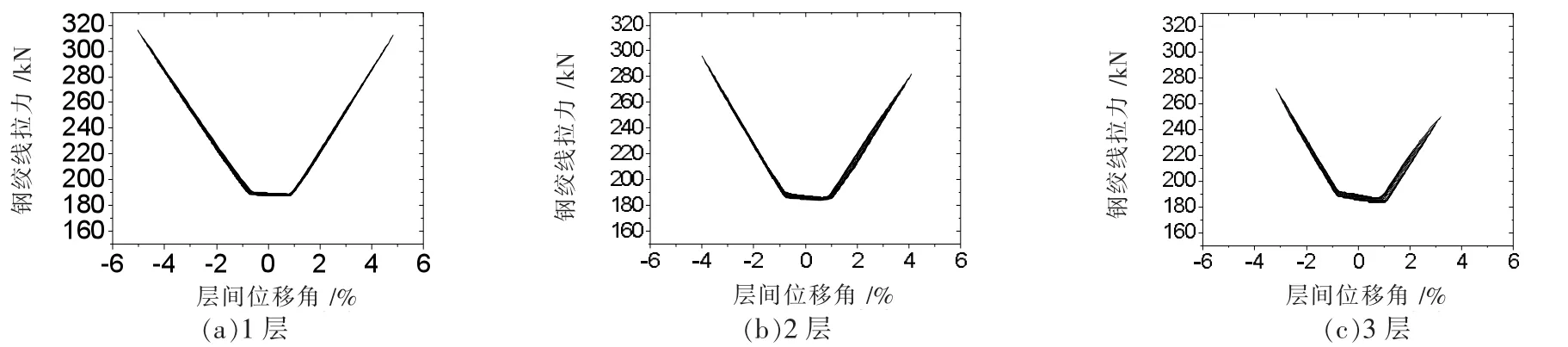
图16 钢绞线拉力值与各层层间位移角间的关系图

图17 耗能钢板剪力与各层层间位移角间的关系图
带蝴蝶型耗能钢板的自复位结构体系中耗能钢板和钢绞线分别提供耗能能力和复位能力,而由耗能钢板、钢绞线、钢框架共同组合,提供了结构所需抗侧力。这些能力又共同反映结构的抗震和复位性能。
通过图15进行结构体系的性能分析。从BASE结构体系的滞回曲线可以看出,曲线呈现典型的“双旗帜型”,且比较饱满,与理论相一致,表明结构具有良好的抗震和复位性能。
纪瑞[11]、经聪[12]曾采用实体单元(ANSYS软件)模拟出单层结构的滞回曲线,文中采用简化模型模拟的滞回曲线与其形状相似。与有限元模型实体模型相比,简化模型建模方便,单层结构模块可以复制,缩短建模时间;应用广泛,实体模型分析时间较长,不利于设计,采用简化模型在运算时间上缩短,由实体模型分析运算的数小时之久缩短为10 min以内,因此可运用于高层带蝴蝶型耗能钢板的自复位结构体系的分析及设计中。
整体分析,加载初期,结构的基底剪力随层间位移角的增大而近似线性增大,说明梁柱节点脱开前,结构刚度基本保持不变,相当于焊接钢框架的刚度,此时整体结构共同抵抗侧向力。当结构荷载增加到965 kN左右,曲线斜率逐渐降低。此时耗能钢板进入塑性耗能,结构刚度由钢绞线提供,钢板充当耗能原件。结构在层间位移角达到4%的情况下,曲线没有下降趋势,仍能承受侧向荷载,且结构仍可复位,说明结构的抗震和复位性能较优。
定量分析,耗能能力和复位能力可分别通过结构能量耗散系数和层间残余位移角来衡量[10]。通过分析计算,经过4%层间位移角的往复加载后,图中BASE结构的能量耗散系数为0.951,说明结构耗能能力较好;结构的层间残余位移角为0.671%,满足自复位结构体系性能设计要求,复位能力较好。表2为不同层间位移角时的结构能量耗散系数,可以看出结构耗能能力先后经历了上升-下降-上升-下降这几个过程。

表2 结构体系能量耗散系数
通过对各层的钢绞线及耗能钢板滞回曲线的分析,细化地分析结构体系的抗震和复位性能。从图16和17中看出,结构体系在承受侧向荷载作用时,每一层的层间位移角从下到上依次减少。这主要是由于每一层所受的侧向力从底部往上依次减少,与地震中的情况类似。钢绞线的受力性能可以从图16看出,由于层间位移角的不同,钢绞线从一至三层,最大拉力依次减少,由于预拉力损失的缘故钢绞线初始预拉力并未达到200 kN。钢绞线拉力值呈线性增长,当结构的层间位移角达到4%的时候,第一层钢绞线的拉力达到310 kN左右。耗能钢板的受力性能可以从图17看出,滞回曲线均比较饱满,说明结构耗能性能较好,滞回环面积从一至三层逐渐减少。
简化模型可以更本质地反映结构体系的抗震和复位机理。综上所述,带蝴蝶型耗能钢板的自复位结构体系具有较好的抗震和复位性能,可应用于高层建筑的抗震中。
4 参数分析
带蝴蝶型耗能钢板的自复位结构体系由钢板提供耗能能力,钢绞线提供复位能力。钢板方面因素包括其刚度及承载力,选取板厚t进行参数分析;钢绞线方面影响因素包括节点转动刚度及钢绞线回复力,选取单束钢绞线数量N进行分析。以BASE结构体系为基础,设计2组系列,分别为BT系列(板厚t不同),LT系列(钢绞线数量N不同),框架梁柱材料按BASE结构体系采用。
采用控制变量的方法,除改变参数的不同,其它参数与BASE结构中相同。BT系列结构中板厚t的参数选取如表3所示,LT系列结构中钢绞线数量N的选取如表4所示。

表3 BT系列参数

表4 LT系列参数
采用循环往复的方式加载(同上节),图18为BT系列结构体系的滞回曲线。可以看出,随着板厚的增加,结构体系滞回环面积不断增加,耗能不断增大,层间残余位移角也不断增加。到达板厚t=30 mm,结构推至层间位移角2.6%时开始计算不收敛,结构无法复位。原因是钢板厚度增大导致钢板侧向刚度增大,而钢绞线回复力不变,到t=30 mm时回复力不足(钢绞线达到屈服应力)。表5分别为板厚为10、15、20、25 mm时(推至4%层间位移角)结构体系的各项性能参数,可以看出在钢绞线回复力满足要求的情况下,结构体系最大承载力、耗能能力、残余变形都不断增加。

图18 BT系列结构体系的滞回曲线

表5 BT系列相关性能参数
图19为LT系列结构体系滞回曲线,可以看出在单束钢绞线数量N分别为3、5根时,结构体系无法推至4%层间位移角,原因是钢绞线回复力不足,无法中和达到相应层间位移角时钢板的剪力;N=3、5时结构可分别可推至层间位移角的 1.00%、3.15%,对应的承载力分别为 873.2、1293.1 kN。表6为 N=7、9、11 时结构体系的各项性能参数,可以看出,当钢绞线回复力充足时,增加钢绞线的数量可使结构承载力和耗能能力增加,但并不显著,而残余变形却出现增大。原因是钢绞线数量增加后梁柱连接更紧密,而推动相同层间位移所产生的侧向力增大,导致钢板产生更大的塑性变形。

图19 LT系列结构体系的滞回曲线

表6 LT系列相关性能参数
综上所述,钢绞线和耗能钢板存在相互制衡的关系,需要相互匹配,参数需相互协调,保持在一定合理范围,结构才能达到较优性能。BT系列中当耗能钢板厚度超过25 mm后,继续增加耗能钢板厚度会造成体系复位性能下降,不能与钢绞线有效匹配;LT系列中当单束钢绞线数量增加至7根时,继续增加对结构体系性能提升很小,不能与耗能钢板有效匹配,造成材料浪费。文中耗能钢板厚度宜取15~20 mm,单束钢绞线根数宜取7根,体系可达到较优的综合性能。
5 结论
(1)提出带蝴蝶型耗能钢板的自复位结构体系简化模型,给出建模方法。通过对试验的验证,证明了建模方法的正确性。(2)建立带蝴蝶型耗能钢板的自复位结构体系简化模型,采用静力非线性的方法对结构进行单向加载,分析表明结构体系的荷载-位移曲线可简化为“双折线”模型;并进行往复荷载下的性能分析,分析得到的滞回曲线呈现典型的“双旗帜型”,符合自复位结构理论。(3)通过计算结构能量耗散系数及层间残余位移角,分析各层钢绞线及耗能钢板滞回曲线,表明带蝴蝶型耗能钢板的自复位结构体系抗侧能力较高,耗能能力较好,具有良好的抗震和复位性能。与有限元模型实体模型相比,简化模型建模方便,计算时间缩短,可运用于高层结构体系的设计中。(4)在钢绞线回复力满足要求的情况下,随着板厚的增加,结构体系最大承载力,耗能能力,残余变形都不断增加;在钢板一定的情况下(钢绞线回复力满足要求),增大钢绞线数量并不能显著提高结构的耗能能力,反而残余变形增加。耗能钢板与钢绞线存在相互制衡的关系,需要相互匹配,进行合理设计,才能使结构发挥较优性能。
参考文献:
[1]MA X.Seismic design and behavoir of self-centering braced frame with controlled rocking and energy-dissipating fuses[M].Stanford University,USA,2010.
[2]程加明.可控摇摆自复位结构体系抗震性能分析[D].苏州:苏州科技大学,2016.
[3]EATHERTON M.Large-scale clclic and hybrid simulation testing and development of a controlled-rocking steel building system with replaceable fuses[C].University of Illinois at Urbana-Champaign,USA,2010.
[4]潘振华.具有自复位能力的钢框架体系研究[D].北京:清华大学,2010.
[5]崔强.利用角钢耗能的自复位结构体系的抗震性能[D].苏州:苏州科技学院,2015.
[6]王琦.钢板剪力墙自复位结构体系的抗震设计方法[D].苏州:苏州科技大学,2016.
[7]中国建筑科学研究院.建筑抗震设计规范:GB 50011-2010[S].北京:中国建筑工业出版社,2010.
[8]中华人民共和国住房和城乡建设部.建筑结构荷载规范:GB 50009-2012[S].北京:中国建筑工业出版社,2012.
[9]樊春雷.钢框架—钢板剪力墙结构基于性能的抗震设计研究[D].西安:西安建筑科技大学,2014.
[10]张磊.钢板剪力墙自复位结构体系的抗震性能分析[D].苏州:苏州科技学院,2015.
[11]纪瑞.蝴蝶形钢板剪力墙—自复位钢框架结构体系性能研究[D].苏州:苏州科技大学,2016.
[12]经聪.利用蝴蝶型钢板剪力墙耗能的自复位结构体系研究[D].苏州:苏州科技学院,2013.
Analysis of seismic performance and recentering of self-centering structural system with infilled butterfly-shaped steel plate walls
ZHU Wenkuan,LI Qicai,HUANG Zizun,CHENG Jiaming
(School of Civil Engineering,SUST,Suzhou 215011,China)
The self-centering structural system with infilled butterfly-shaped steel plate walls is a new seismic structural system which combines the energy dissipation capacity of energy dissipation steel plate and recentering performance of self-centering nodes.The paper proposed a simplified model and the modelling,and used a stimulation-based verification by an experimental model.A structural modelling was made by the simplified model,and to better understand the mechanical properties of perforated steel plate shear wall and verify the correctness of the theoretical formula,the static nonlinear method was used to perform the cyclic loading to the structure.The results show that the hysteretic curve of the structure is plump.The calculation of the energy dissipation factor of the structure and the interlayer residual displacement angle shows that when the structure has a stronger side resistance and a better energy dissipation capacity,it can meet the design requirement of the self-centering structural system.Compared with the practical model of the finite element,the simplified model is convenient and widely used.The parameter analysis of the structural system shows that the butterfly-shaped steel plate wall and the prestress steel strand need to match each other so as to make the structure system performance give a full play.
perforated steel plate shear walls;structural system of self-centering;static nonlinear method;hysteretic curve;Opensees
TU391
A
2096-3270(2017)04-007-07
2016-02-28
国家自然科学基金项目(51378326);江苏省结构工程重点实验室开放课题(ZD1204)
诸文宽(1992-),男,江苏常州人,硕士研究生。
李启才(1969-),男,副教授,博士,从事钢结构的新型结构体系和抗震设计研究,Email:ustsgjg@163.com。
秦中悦)

