基于三维数字图像相关的双轴振动疲劳试验研究

魏良宝，蒋 明

（苏州科技大学 土木工程学院，江苏 苏州215011）

基于三维数字图像相关的双轴振动疲劳试验研究

魏良宝，蒋 明

（苏州科技大学 土木工程学院，江苏 苏州215011）

为研究双轴振动疲劳下，构件裂纹区域位移与应变场的变化规律，本试验采用双轴振动疲劳装置与数字采集系统实时监测裂纹区域。由高速数字图像相关系统采集一系列正弦交变载荷作用下预制裂纹梁试件裂纹周边区域的序列数字散斑图像，应用三维数字图像相关技术获取试件固有频率的变化、预制裂纹尖端区域的位移场及应变场。通过对预制裂纹尖端区域在不同循环周期下离面位移、主应变、离面应变变化的分析，获得位移、应变与循环周期之间的变化规律。

振动疲劳；三维数字图像相关；双轴振动；位移场；应变场

工程结构在服役中，由于受外界激励的长期作用，将会产生振动和疲劳的问题，这些激励通常来自多个方向，例如风-车-桥振动耦合，水立管双向水流振动影响等。由此导致的结构振动疲劳损伤研究变得更加复杂。

焦群英等[1]论述了共振疲劳与强迫振动疲劳的差异，强调了共振疲劳与结构的动态特性关系并且论述了利用应变模态分析的结果确定共振疲劳危险点位置原理。刘文光等[2-3]为提高裂纹板的振动疲劳分析精度，提出一种振动疲劳裂纹扩展耦合分析的方法，以及一种裂纹梁的振动疲劳与裂纹扩展相结合的分析方法；王锦丽等[4]研究了加载频率对悬臂梁振动疲劳特性的影响，得出加载频率对振动疲劳寿命有较大的影响；李光强[5]以南广铁路新建郁江钢桁梁斜拉桥为案例，研究了在风与列车荷载共同作用下钢桁梁斜拉桥的竖向振动和斜拉索、关键杆件的疲劳损伤和疲劳寿命问题；张磊安等[6]提出了一种基于电驱动模式的双轴共振疲劳加载方式；蒋培等[7]对传统振动台的单轴依次加载和目前的多轴振动台的多轴同时加载模式进行比较分析，研究不同形式加载对疲劳裂纹应力强度因子的影响，最终得到多轴振动同时加载比单轴依次加载对疲劳破坏影响更大。张莉等[8]应用有限元法和疲劳损伤累积理论对6种损伤参数进行修正，计算得到了单轴、多轴比例与非比例循环载荷作用下疲劳损伤累积规律，建立了一种损伤演化方程，估算疲劳寿命。

Mahdi Heydari等[9]提出一个连续双线性模型来研究裂纹梁的强迫弯曲振动，该模型考虑了转动惯量和剪切变形的影响，由该模型所提出的方法而得到的频率响应与有限元所得结果对比验证了该方法的准确性；Masayuki Kamaya[10]得出小面积屈服和大面积屈服条件下应变强度因子是一个有效参数，来预测裂纹扩展；A.J.Dentoras和A.D.Dimarognas[11]提出由于裂纹进而影响了在下一个外力在恒定的振幅和频率下的系统动态响应，裂纹深度决定了自身的弹性。裂纹扩展导致连续系统附加深度的产生，这导致结构远离共振区域从而导致裂纹区域受力变小，出现动态止裂现象；O.Plekhov[12]等在实验和理论方面研究了在循环载荷下的裂纹扩展，通过实验数据的分析得出在裂纹尖端塑性变形区和能量耗散的变化；M.Krawezuk[13]等对裂纹旋转梁的自由振动通过进行有限元的分析得出裂纹可以改变系统的固有频率；M.Bachene等[14]使用扩展有限元的方法来对裂纹板进行振动分析，数值分析结果与实验结果吻合比较好。本研究运用三维图像相关技术，对预制裂纹梁进行单轴、双轴振动疲劳试验，获得了试件固有频率的变化以及预制裂纹周边微小区域的位移场和应变场，对比了单轴与双轴疲劳振动中固有频率的变化；分析了裂纹的萌生以及扩展机理，最终获得双轴振动疲劳的位移、主应变与循环周期数之间的变化关系。

1 三维数字图像相关基本原理

三维数字图像相关方法是基于双目立体视觉原理和数字图像相关匹配技术的三维变形测量方法。如图1所示，由两个互成一定角度的相机同步拍摄喷有人工散斑的被测物表面，通过分析左右相机记录的散斑图像，运用图像相关运算获得以被测点为中心的图像子区在左右图像中对应的位置，根据相机标定获得的左右相机的内外参数，建立空间几何关系，从而实现试件表面的三维重建[15]。

图1 三维数字图像相关测量原理图

用来比较图像变形前后子区域相似程度的相关函数为[16]

其中，f（x，y）和 g（x′，y′）分别为图像子区变形前后的灰度值，分别为参考图像子区和目标图像子区的灰度平均值，即

2 试验概况

2.1 试验系统

试验系统主要由NI数据采集控制系统、功率放大器、激振器、三维图像相关系统、试件以及约束装置组成。图2为振动疲劳试验系统；图3为NI数据控制和存储系统。

图2 双轴振动疲劳试验系统

图3 NI数据控制和存储系统

试验所用试件为6061铝合金材料制作，尺寸为250 mm×10 mm×4 mm，分别在试件的激振点左右18 mm位置处预制一贯穿裂纹，长度为1 mm，如图4所示。在疲劳加载过程中，为了保证激振器与试件的连接，同时保证试件能够出现裂纹扩展以及图像采集方便，设定在距离预制裂缝18 mm的位置加载。由于试件在X方向（见图4）固有频率较大，为了保证以试件的固有频率激振时，振动疲劳过程稳定，在试件自由端部加一尺寸为50 mm×20 mm×12 mm的配重，重量为90 g。试验前在试件一侧预制裂纹区域制作人工散斑。试件1、试件2以及配重尺寸如图4所示。

图4 试件及配重尺寸

在振动疲劳试验过程中，设定试件一端固定，一端自由，其中固定端通过多排螺栓的连接来实现，与此同时将试件一端伸入夹具里50 mm，并在试件伸入端钻两个螺栓孔，使得试件与夹具能够更好的连接，整个固定端通过两片夹具压力达到的摩擦力以及螺栓的剪切力来实现试件在振动疲劳过程中保持完全固定，不会发生侧移，最终保证试验的可靠性。夹具尺寸如图5所示。

图5 夹具尺寸

2.2 固有频率测量

实验采用数字图像相关的方法来获得试件的固有频率，用力锤敲击试件使其自由振动，通过高速摄像机记录下试件自由振动图像，根据图像相关方法得出试件的各点位移变化，最后通过模态分析软件计算，得到试件的一阶固有频率。

2.3 试验工况

单轴振动疲劳试验沿X方向激振，激振点加速度为（1.25±0.05）g；双轴振动疲劳试验沿X方向及Z方向双向激振，X方向加速度（1.25±0.05）g，Z方向电压值2 000 mV。单轴、双轴振动疲劳加载时间均为150 min（即527 346个疲劳循环）。方向坐标见图4。

2.4 振动疲劳试验过程

振动疲劳试验前，将力传感器置于激振器顶杆上，用于测量记录在激振过程中激振力大小的变化；将加速度传感器用502胶粘贴在激振器平台上，试验过程中控制加速度保持不变。由高速三维数字图像相关系统实时采集裂纹区域的序列图像，其中高速三维数字图像相关系统由两组分辨率为600×800像素的高速摄像机（型号：MIRO-3M）和75 mm镜头（型号：Titanar A 75）配套260 mm接圈及同步采集控制器组成。实时图像采样频率为1 000对/s，视场范围为6 mm×8 mm；图像计算子区大小设定为19×19像素，计算网格步长为11×11像素，计算精度为50 με。由三维图像相关计算分析序列图像，获取在振动疲劳过程中裂纹的扩展以及所在区域点的位移、应变的变化。

试验过程流程图见图6，在控制面板中设置加载频率与试件固有频率一致，从NI设备发出信号源，经过NI数据采集系统传递到功率放大器，然后驱动激振器以试件的固有频率进行正弦式的激振，在振动过程中通过功放调节对结构的应力响应进行控制，使其振动加速度基本保持不变。在软件控制窗口分别对激振力、加速度值信号等进行存储记录。对于试件振动疲劳过程中应变信号的记录过程采用分段式，根据试件固有频率设定整个过程采样频率为1 000 Hz。每激振30 min休息10 min，在激振的30 min中每隔10 min记录一次，共4个记录时段，每个时段时长4.418 s，试件在振动疲劳达到150 min（即527 346个疲劳循环）后停止试验，并再次测量振动疲劳之后试件的固有频率。

3 试验结果分析

3.1 试件固有频率变化

试件单轴振动疲劳加载形式及疲劳振动前后的固有频率列于表1。通过比较相同的激振点位置，不同预制裂纹位置的试件固有频率下降比较可知，试件中裂纹处于固定端与激振点之间时，试件的疲劳寿命要比预制裂纹在激振点另一侧长；通过振动形式可以看出试件中裂纹的扩展主要是通过自身的自由振动来实现的。

双轴振动疲劳同时在试件的X方向与Z方向进行激振。为了保证双轴之间的联动，将两个激振器连接在一起，同时为了能够通过传感器得到数据对试验进行控制，在Z方向激振力相对小一些。试验结果列于表2。从X方向固有频率变化可知试件在双轴振动疲劳中，固有频率要比单轴下降的多，说明试件在双轴振动疲劳时寿命要比单轴振动疲劳要小。但由于Z方向振动幅值较小，试件裂纹的扩展基本以X方向振动疲劳为主，Z方向固有频率的施加，使得振动疲劳裂纹扩展加速，从而使得X方向固有频率加速下降。

表1 试件单轴振动疲劳的X方向固有频率变化表（527 346疲劳循环周期）

表2 试件双轴振动疲劳的固有频率变化表（527 346疲劳循环周期）

3.2 双轴振动疲劳裂纹区域的位移、应变场分析

以试件1进行分析。整个试验过程共记录22个时段，在每个时段选取最后一个循环周期的正向位移最大时刻的22对图像进行三维图像相关计算，图7为对应的振动疲劳不同时刻预制裂纹区域的主应变云图。

从振动疲劳最大正向位移时的主应变云图中选取预制裂纹尖端点，得到振动疲劳过程中主应变的变化曲线，如图8所示，在试件达到118 min（即414 845个疲劳循环）之前，预制裂纹尖端点主应变基本保持不变，之后试件的主应变值呈缓慢增长。选取各个时段最大正向位移与最大负向位移时的图像进行主应变计算，如图9主应变云图，在主应变云图上选取预制裂纹尖端点，得到振动疲劳过程中正向最大位移与负向最大位移时主应变的变化曲线，其趋势与主应变变化趋势基本一致。

从振动疲劳加载过程中选择两个时间段的图像进行图像相关计算，这两个时间段分别是第4分钟（即14 062个疲劳循环）以及第148分钟（即520 314个疲劳循环），得到这两个时间段位移云图，如图10所示，从预制裂纹尖端点Y方向位移变化曲线可知，振动疲劳过程中试件Y方向位移变化都保持正弦加载的形式；从Y方向最大正向位移与最大负向位移时位移云图可知，沿试件长度方向从左到右位移值逐渐减小。从图11位移云图可知，在Z方向最小位移时，预制裂纹区域位移场数值一致，没有发生变化，而在Z方向最大位移时，可以看到Z方向位移值由预制裂纹处到另一侧逐渐减小，并且可以观察到预制裂纹处位移最大且是正向的，而另一侧位移呈负向且值较小，说明在Z方向振动疲劳过程中预制裂纹处Z方向位移比较大。从预制裂纹尖端点Z方向位移曲线可知，整个加载过程Z方向位移曲线基本保持正弦加载的形式，只是其中波动性较大，这主要是因为试件X方向加载力对其的影响较大。

图7 振动疲劳过程中正向最大位移时的主应变云图

图8 预制裂纹尖端点主应变变化曲线

图9 预制裂纹尖端点主应变幅值变化曲线

图10 预制裂纹尖端点Y方向位移曲线与位移云图

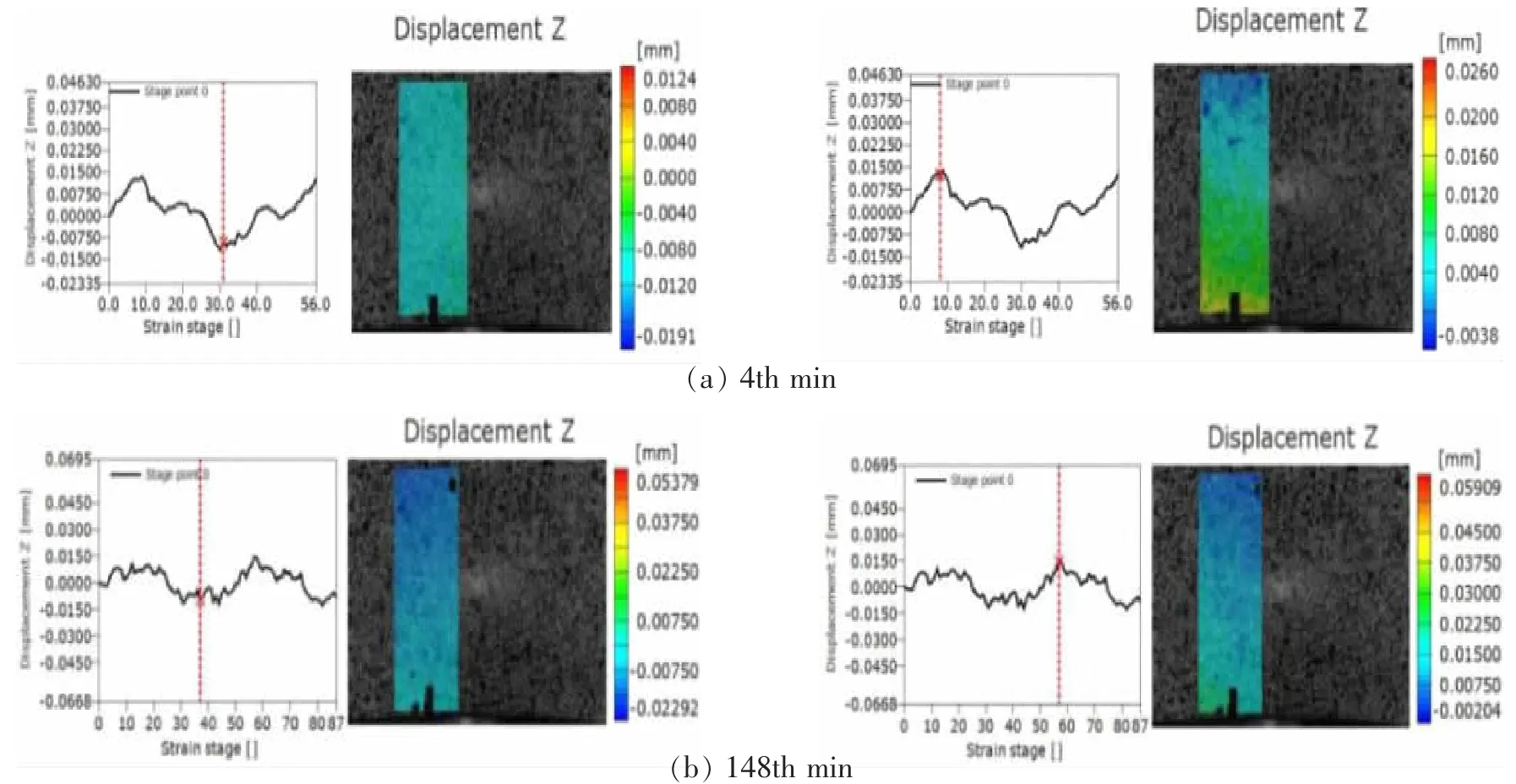
图11 预制裂纹尖端点Z方向位移曲线与位移云图

如图12所示对预制裂纹尖端点主应变曲线分析，随着加载循环的继续，使得裂纹开始扩展，主应变集中区域变大，这时在预制裂纹处的主应变值呈现正向主应变值快速增大，应变集中现象非常明显，此时预制裂纹处完全进入塑性变形。对于预制裂纹尖端点离面方向应变曲线变化，如图13所示，裂纹未出现或刚刚出现时，预制裂纹处的离面方向应变曲线基本为正弦式的加载形式，虽然波动性很大，但随着加载循环的继续，使得裂纹开始扩展，离面方向应变集中区域变大，这时在预制裂纹尖端点离面方向应变值呈快速增大，其曲线变化规律与主应变变化规律相一致。

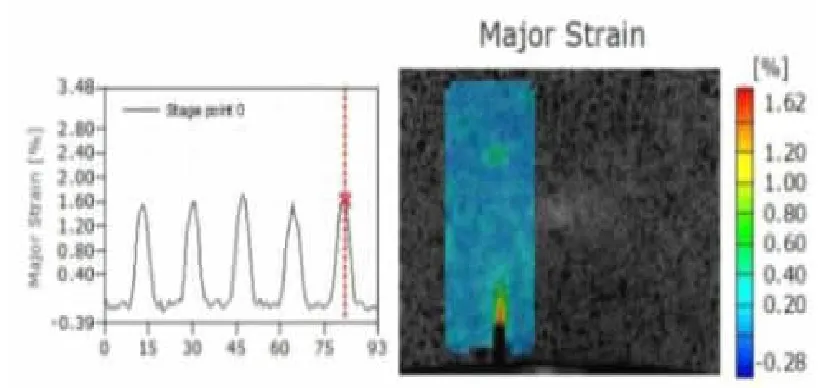
图12 预制裂纹尖端点主应变变化曲线及主应变云图

图13 预制裂纹尖端点离面方向应变变化曲线及应变云图

4 结语

在相同的激振时间下，双轴振动疲劳下试件的固有频率要比单轴振动疲劳下降多1.17%和1.69%，双轴振动疲劳下试件比单轴振动疲劳更容易破坏。

双轴振动疲劳试验中，一轴方向振动疲劳加载力很小，其对试件固有频率下降仍有推动作用，并且其主应变与主应变幅值变化曲线与单轴有较大激振力时的变化曲线一致，即双轴振动疲劳中若有一轴激振力较小则可将双轴简化为单轴较大激振力时的疲劳计算。

在振动疲劳过程前期，预制裂纹尖端点的主应变值基本不变，随着振动疲劳加载继续，主应变值缓慢增长，主应变幅值也有同样的变化规律。

[1]焦群英，王书茂，才力，等.用于结构共振疲劳寿命估计的应变模态分析[J].机械工程学报，1996（3）：52-57.

[2]刘文光.考虑结构裂纹扩展的振动疲劳寿命计算方法[J].振动工程学报，2012，25（1）：79-83.

[3]刘文光，陈国平.含裂纹悬臂梁的振动与疲劳耦合分析[J].振动与冲击，2011，30（5）：140-144.

[4]王锦丽，李玉龙，胡海涛，等.加载频率对悬臂梁振动疲劳特性的影响[J].振动与冲击，2011，30（6）：243-247.

[5]李光强.风与列车荷载作用下钢桁梁斜拉桥竖向振动及疲劳研究[D].长沙：中南大学，2013.

[6]张磊安，王忠宾，刘卫生，等.基于两轴共振模式的风电叶片疲劳加载监控系统设计[J].河北科技大学学报，2016，37（1）：7-12.

[7]蒋培，张春华，陈循.多轴载荷对疲劳裂纹的影响[J].机械研究与应用，2005（1）：45-46.

[8]张莉，唐立强，付德龙.基于损伤累积理论的多轴疲劳寿命预测方法[J].哈尔滨工业大学学报，2009，41（4）：123-125.

[9]HEYDARI M,EBRAHIMI A,BEHZAD M.Forced vibration analysis of a Timoshenko cracked beam using a continuous model for the crack[J].Engineering Science&Technology An International Journal,2014,17（4）：194-204.

[10]KAMAYA M.Low-cycle fatigue crack growth prediction by strain intensity factor[J].International Journal of Fatigue,2015,72：80-89.

[11]DENTSORAS A J,DIMAROGONAS A D.Resonance controlled fatigue crack propagation in a beam under longitudinal vibrations[J].International Journal of Fracture,1983,23（1）：15-22.

[12]PLEKHOV O,FEDOROVA A,KOSTINA A,et al.Theoretical and experimental study of strain localization and energy dissipation at fatigue crack tip☆[J].Procedia Materials Science,2014,3（4）：1020-1025.

[13]KRAWCZUK M.Natural vibration of cracked rotating beams[J].Acta Mechanica,1993,99（1-4）：35-48.

[14]BACHENE M,TIBERKAK R,RECHAK S.Vibration analysis of cracked plates using the extended finite element method[J].Archive of Applied Mechanics,2009,79（3）：249-262.

[15]唐正宗，梁晋，肖振中，等.用于三维变形测量的数字图像相关系统[J].光学精密工程，2010，18（10）：2244-2253.

[16]代坤.数字图像相关测量方法及试验研究[D].长沙：长沙理工大学，2014.

Experimental study on biaxial vibration fatigue based on 3D digital image correlation

WEI Liangbao,JIANG Ming
（School of Civil Engineering,SUST,Suzhou 215011,China）

In order to study the variation of the displacement and strain field of the crack region under the biaxial vibration fatigue,the experiment adopted the biaxial vibration fatigue device and the digital acquisition system to monitor the change of the crack area in real time.A series of digital speckle images of the prefabricated cracked beam specimen under the series of sinusoidal alternating loads were collected by the highspeed digital image correlation system,and the 3D digital image correlation technique was used to calculate the natural frequency of the specimen,the displacement field and strain field in the crack tip region.The change of the displacement direction,the main strain and the strain in the direction of the surface of the prefabricated crack were analyzed under different cycle periods,and the change rule between displacement,strain and cycle was obtained.

vibration fatigue;three-dimensional digital image correlation;biaxial vibration;displacement field;strain field

经朝明）

TH113.1

A

2096-3270（2017）04-0032-08

2017-05-26

国家自然科学基金项目（11172193）

魏良宝（1990-），男，江苏扬州人，硕士研究生。

蒋 明（1961-），女，江苏苏州人，教授，博士，主要从事光测力学，振动疲劳研究，Email:jiangming@mail.usts.edu.cn。