基于线性插值函数的二维异构网格数据插值方法研究

刘 刚， 池 骋， 孙立鹏， 马永强， 李 琳

(1.华北电力大学 河北省输变电设备安全防御重点实验室，河北 保定 071003;2.华北电力大学 新能源电力系统国家重点实验室，北京 102206)

基于线性插值函数的二维异构网格数据插值方法研究

刘 刚1， 池 骋1， 孙立鹏1， 马永强1， 李 琳2

(1.华北电力大学 河北省输变电设备安全防御重点实验室，河北 保定 071003;2.华北电力大学 新能源电力系统国家重点实验室，北京 102206)

在多物理场耦合仿真中，由于各个物理场对网格类型、疏密的要求有很大差异，不同物理场仿真时往往使用不同剖分网格，即异构网格。针对异构网格单元和节点不匹配的情况，提出基于线性插值函数映射的方法来解决二维多物理场耦合仿真时的数据传递问题。同时对位于曲线边界上待插值节点不在三角形内部的问题，提出了反距离加权插值的解决方案。分析了网格粗细对插值精度的影响，验证了基于线性插值函数的方法在二维异构网格数据映射时的有效性。同时利用该算法，将换流变压器阀侧绕组端部温度结果映射到电场仿真模型中，为研究温度分布不均匀条件下的二维复合电场奠定了基础。

异构网格； 三角形剖分； 线性插值； 多物理场耦合

0 引 言

在多物理场耦合仿真中，如油浸式变压器二维电磁场和流体-温度场耦合分析，电磁损耗作为温度场的热源，对流体-温度场的分布有重要影响[1-2]，传统平均热源的方法虽然给流体-温度场仿真带来了方便[3-6]，但是热源平均化处理可能会使仿真得到的局部热点同实际分布有所偏差，容易导致计算得到的绕组局部热点与实际不同。因此为准确地得到流体-温度场分布，在流体-温度场仿真时必须准确地掌握热源(即损耗密度)的分布情况。同时温度对铁磁材特性和绕组电导率油也有影响，如果计算模型也将区域中温度平均化处理，则由平均温度得到的参数将与实际的物性参数明显不同，也可能导致电磁场计算结果与实际有所偏差。

因此耦合仿真分析时，需要准确地将电磁场、流体-温度场的计算数据相互传递。但是电磁场和流体-温度场计算时所建立的仿真模型和剖分网格往往不同，即异构网格。此时磁场的单元损耗结果不能直接作为流体-温度场单元的热源，流体-温度场的单元温度结果也不能直接作为电磁场单元的温度。如果电磁场和流体-温度场建立统一的有限元模型，则必须同时兼顾各物理场对网格形状和精度的要求，这样便需要对计算机的硬件提出极为苛刻的要求[7]。因此需要研究异构网格间节点数据的映射方法，将电磁场损耗准确映射到流体-温度场相应网格单元中，以准确地得到流体-温度场模型中热源的分布；将流体-温度场的温度准确地映射到电磁场相应单元网格，以准确地得到电磁场单元的温度分布。

目前，虽然很多商业多物理场仿真软件(如ANSYS WorkBench、COMSOL Multiphysics和CST MICROWAVE STUDIO等)为多物理场耦合计算带来了极大的方便[8-10]，但其自带的数据映射方法、原理和代码往往是不公开的，无法有效地针对特定问题开展有效地研究，不同物理场耦合时异构网格数据的映射精度可能无法得到保证。

异构网格间节点数据的映射可归结为多元数据插值或拟合问题。对于这类问题，工程中已经发展出许多方法，如最近邻法、快速壳法[11]、径向基函数法[12]和反距离移动平均[13]等。其中，最近邻法原理简单，但是精度不高，尤其网格剖分较稀疏时误差较大；快速壳法插值速度快，精度高而灵活，但是只能对凸壳内的点插值；径向基函数法数学概念清晰，方法简单，计算精度高，但其在数值大小波动范围大的情况下，对数值较小的节点插值精度较差；反距离移动平均法算法简单高效，可以计算任何值，但是精度不好。

本文基于有限元的等参元理论，提出利用线性插值函数实现二维电磁场和流体-温度场之间的数据传递，并用反距离加权方法实现凸边上待求节点无法插值的问题。为验证算法的可行性，本文基于具有解析解的算例，对算法的映射精度进行了分析比较，分析了网格剖分疏密程度对映射算法计算精度的影响。最后利用本文算法所开发的程序，将换流变压器流体-温度场仿真模型中的电场计算结果映射到相应的电场计算模型，从而为分析不同温度下的二维复合电场奠定了基础。

1 算法原理

异构网格节点数据的映射，在数学上可以等效为插值问题，即利用已知物理场节点的物理量，对未知物理场节点通过插值方法，获得满足精度要求的物理量[14]。在有限元分析中，基于线性插值函数，不仅可以对各个剖分单元内某点的物理量进行局部插值，还可以对节点坐标进行插值分析。本文所提方法的思路是：对于未知物理场的每一个待求节点，寻找其在已知物理场上对应的三角形单元，称之为备选主单元，然后利用备选主单元各节点对未知物理场节点的物理量进行插值，如图1所示。

图1 快速映射法示意图Fig.1 Diagram of the fast projection algorithm

首先，遍历已知物理场的所有单元，寻找待插值节点D对应的备选主单元，在图1中，ijk单元是未知物理场网格中待求节点D的一个备选主单元，i，j，k为备选主单元的三个节点，(xi，yi)，(xj，yj)，(xk，yk)为已知物理场主单元各节点坐标，设x，y为未知物理场节点坐标，则由有限元的等参元理论可知，待求点如果在主单元内部，则满足如下关系式：

(1)

对于位于主单元内部的节点，上式中的形状函数Nm(m=i，j，k)满足：

Ni+Nj+Nk=1

(2)

因此可得：

Nk=1-Ni-Nj

(3)

将式(3)带入到式(1)，整理可得：

(4)

求解式(4)即可得到Ni、Nj，若满足式(5)条件：

0≤Nk≤1，(k=i,j,m)

(5)

则未知物理场节点在备选主单元内或其边界上，此时可根据式(6)对未知物理场节点物理量进行插值,得到待插值节点的物理量为

φsD=Niφfi+Njφfj+Nkφfk

(6)

式中：jfi，jfj，jfk为已知物理场三角形单元各节点物理量值。

若未满足条件(5)，则选取下一个单元进行判断，一直找到每个未知节点对应的主单元为止。

2 模型及参数

本文以单芯同轴电缆的静电场为例[15]，如图2所示。

图2 单芯同轴电缆模型Fig.2 Single core coaxial cable model

设其长度远远大于截面半径，已知内、外半径分别为a和b，中间介质介电常数为e，则内外半径之间任一点的电位为

(7)

由于电场分布满足对称性，因此只取其四分之一进行仿真。分别采用三角形和四边形网格对其剖分，为了分析网格疏密对插值精度的影响，三角形和四边形网格分别采用了疏密两种剖分方式，剖分网格图分别如图3和图4所示。

图3 三角形剖分Fig.3 Triangular meshing

图4 四边形剖分Fig.4 Quadrilateral meshing

3 凸边节点处理

通过分析发现，由于有限元剖分软件得到的三角形或四边形的边往往由直线段组成，而当待插值节点位于凸边的边界上时，就可能找不到相应的主单元，如图5所示，当待插值节点D位于曲边界上时，由于此时此节点D位于单元iel之外，通过式(4)求得形函数不满足式(5)，因此无法利用式(6)进行插值得到待插值节点D的物理量。所以在程序运行结束时，边界上出现待插值节点物理量为零的奇点。

图5 待插值节点不在主单元内部Fig.5 Interpolated node is not inside the master meshing

值得注意的是，剖分软件“以直代曲”的处理方式使得本该在曲边ij上的节点D位于直线段ij之外，因此对于待插值节点物理量，可以根据D点两侧节点i和j进行插值，本文采用反距离加权的方式。具体处理如下：

设(xfi，yfi)，(xfj，yfj)，分别为边界上已知物理场节点i、j坐标，(xsD，ysD)为待求的未知物理场节点D坐标。使用已知数据与改点距离的远近作加权平均，根据上述坐标可以得待插值点与已知函数值节点的距离为

(8)

则待插值函数的值为

φsD=wiφi+wjφj

(9)

4 有效性验证

4.1 三角形映射到四边形

根据剖分网格的坐标，根据式(7)分别算出粗、细三角形单元各节点的电位值，然后利用本文方法得到图4(a)粗剖四边形网格单元的节点电位值，为判断插值效果，本文利用相对误差来衡量各点的插值效果，即：

(10)

式中：jSD为插值得到的节点电位值；jA为根据四边形节点坐标由式(7)得到的解析值。图6和图7分别给出了由图3所示的粗、细三角形网格映射到图4(a)四边形网格节点时的相对误差图。

图6 三角形粗剖插值时的相对误差Fig.6 Interpolation relative error for the triangular coarse mesh

图7 三角形细剖插值时的相对误差Fig.7 Interpolation relative error for the triangular fine mesh

4.2 四边形映射到三角形

二维流体-温度场仿真时，由于结构复杂，往往采用四边形网格或四边形-三角形混合的网格，如图4所示，而磁场或电场仿真时往往采用三角形网格，如图3所示，如果想将流体-温度场的温度计算结果映射到电场或磁场计算模型的单元中，则会涉及到四边形网格数据向三角形网格节点映射的问题。

当备选主单元为四边形单元时，式(4)～(6)不再适用，为此本文提出将一个四边形单元分解为2个三角形单元，例如当剖分单元的节点k和节点m的值不相等时，则相应的剖分单元为四边形单元，此时可以将四边形单元分解为两个三角形单元，如图8(b)为分解方案之一。

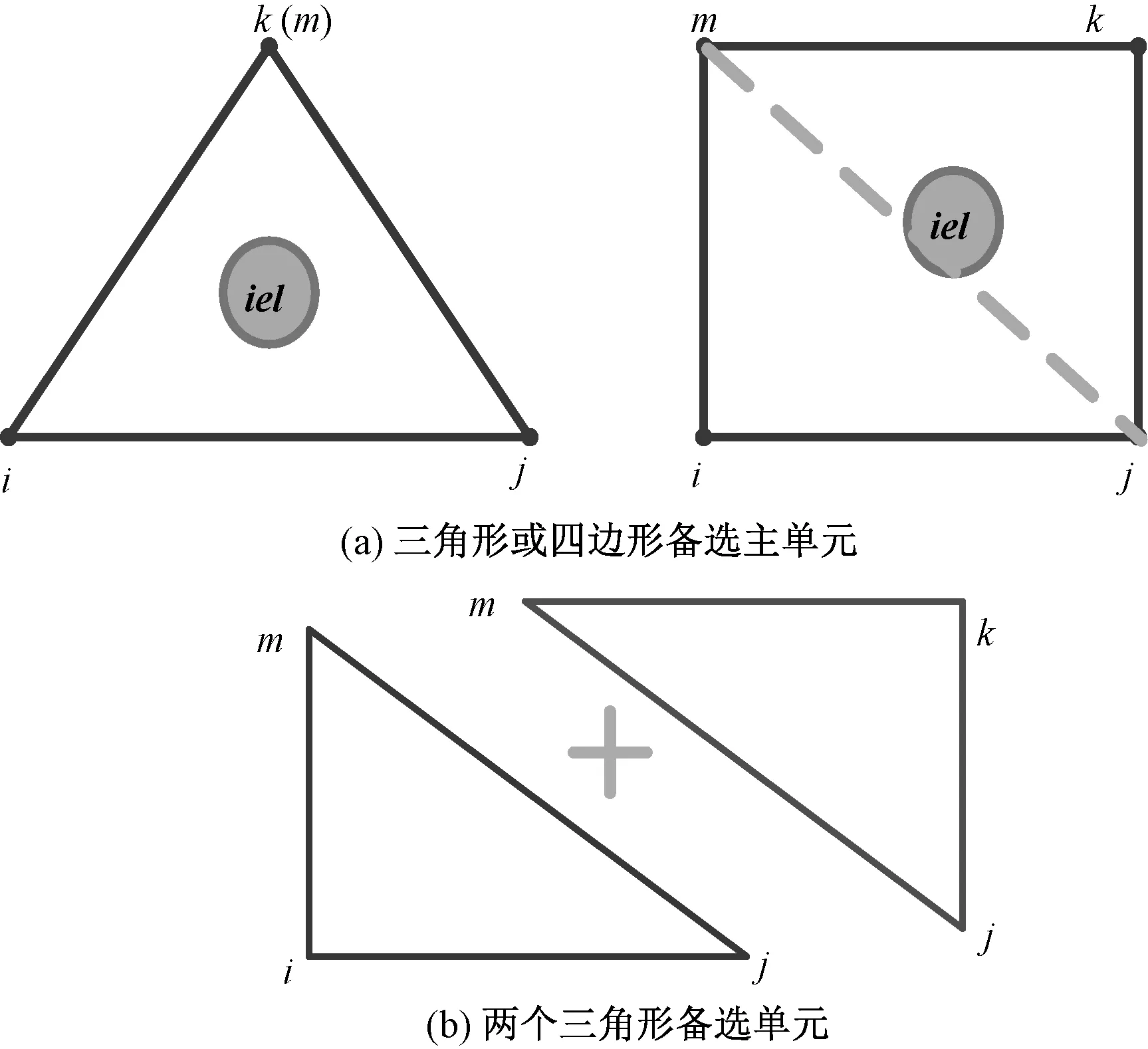
图8 四边形单元分解图Fig.8 Decomposition for the quadrilateral mesh

得到分解的三角形ijm和jkm后，则可以利用上文所推荐的方法来判断备选主单元和节点数据插值。图9和图10分别是由图4所示的粗、细四边形网格映射到图3(a)三角形节点时的相对误差图。

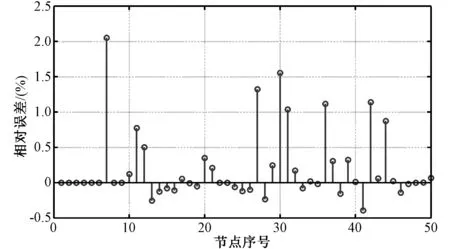
图9 四边形粗剖插值时的相对误差Fig.9 Interpolation relative error for the quadrilateral coarse mesh

图10 四边形细剖插值时的相对误差Fig.10 Interpolation relative error for the quadrilateral fine mesh

从图6、图7和图9、图10可知：

(1)无论是三角形网格还是四边形网格，在网格剖分较粗时，待求节点插值结果的相对误差较大，但最大的相对误差仍小于5%；

(2)当网格剖分较密时，待求节点插值结果的相对误差较小，此时最大相对误差均小于0.10%。

在电磁场仿真中，由于绕组和结构件往往需要考虑涡流效应，因此剖分较密的三角形网络；而流场-温度场仿真时，为了方程组迭代收敛和抑制非物理振荡，需要剖分较密的四边形网格或四边形-三角形混合网络。在两个物理场网格数据的映射过程中，本文提出的数据映射方法得到的计算结果可以满足工程需要。

5 应 用

换流变压器阀侧绕组端部结构复杂，其电场分布是分析的重点，现有分析中常常采用室温(20oC)假设，即设油纸电导率在电场分析时不受温度影响。而实际换流变压器由于铁心和绕组的损耗未必均匀，其内部温度场分布往往不同。但是温度平均化假设得到的电场计算结果与实际电场分布有一定的差异。为此，本文首先使用流体仿真软件Fluent计算了一台±500 kV换流变压器的流场和温度场[16]，流体-温度场仿真时对仿真模型进行适当的简化，仿真结果如图11所示，左侧是部分油道的速度云图，右侧是二维截面温度分布。然后采用本文所提方法将温度场数据映射到电场计算模型，电场计算模型是换流变压器的端部，包含纸板、绝缘层、角环、垫块和变压器油等结构。映射得到的温度分布不均匀的电场计算模型如图12所示，对比图11(c)和图12可以发现，电场计算模型中温度场分布与流场-温度场端部的温度云图一致。基于图12可以进一步分析温度不均匀条件下的绝缘电场。

图11 流场-温度场仿真结果Fig.11 Computational results of fluid-thermal field

图12 电场模型中的温度分布Fig.12 Temperature distribution in electric model

6 结 论

本文提出基于线性插值函数的异构网格数据映射算法，利用反距离加权法实现了凸边节点的插值。所提方法在剖分网格较稀疏时，插值结果的误差较大，但最大相对误差仍小于5%；而当剖分网格较密时，节点插值的精度较高，最大相对误差均小于0.10%。

运用本文方法将换流变压器流场-温度场模型中的温度场数据映射电场仿真模型，为进一步研究不同温度下的电场分布奠定了基础。

[1] 肖强，王红艳，陈晴，等．油浸式电力变压器内部温度场与流场特性分析[J]．南京工程学院学报(自然科学版)，2016，14 (1)：60-64．

[2] 李伟力，孙佳慧，孙宏丽，等．汽轮发电机稳态与负序工况下转子涡流损耗计算和温度场分析[J]．电工技术学报，2012，27 (9)：59-63．

[3] 景崇友，王建民，陈志伟，等．换流变压器绕组瞬态漏磁场与谐波损耗的分析[J]．变压器，2007，44 (4)：1-4．

[4] 刘旸．大型换流变压器损耗分析与计算[D]．哈尔滨：哈尔滨理工大学， 2010．

[5] 刘赟，俞集辉，程鹏．基于电磁-热耦合场的架空输电线路载流量分析与计算[J]．电力系统保护与控制， 2015， 43 (9)：28-34．

[6] 陈浩．换流变压器铁芯饱和不稳定及温升问题研究[D]．北京：华北电力大学， 2012．

[7] 张宇娇，秦威南，刘东圆，等．面向电磁装置磁-热耦合分析的异型网格映射方法[J]．电工技术学报，2016， 31 (13)：141-148．

[8] 仲留寄，王金娥．基于Comsol的离相封闭母线短路电动力的计算[J]． 电力科学与工程，2016，32 (3)：22-25，48．

[9] 李宜伦，王泽济，杨仕友，等．热轧带钢厂边部加热涡流温度场仿真分析[J]． 电工技术学报，2013，28 (增刊)： 105-110．

[10] 石碧薇．变压器在谐波条件下的损耗及热问题分析[D]．保定：华北电力大学，2014．

[11] BARBER C B，DOBKIN D P，HUHDANPAA H T．The quick hull algorithm for convex hulls [J]．ACM Transactions on Mathematical Software， 1996，22 (4)：469-483．

[12] 孙学功．多物理场耦合界面数据传递的仿真研究[J]． 计算机仿真， 2015，32 (1)：23-28．

[13] 宋少云，李世其．耦合场协同仿真中节点载荷插值的混合法[J]．计算机仿真，2006， 23 (8)：73-75，125．

[14] 吴宇飞，王跃方，孙兴华．径向基函数插值在叶轮流固耦合分析中的应用[J]．风机技术，2012,(3)：34-39．

[15] 倪光正，杨仕友，钱秀英，等．工程电磁场数值计算[M]．北京：机械工业出版社，2004．

[16] YATSEVSKY V A．Hydrodynamics and heat transfer in cooling channels of oil-filled power transformers with multicoil windings[J]．Applied Thermal Engineering， 2014，63 (1)：347-353．

Research on Data Interpolation for 2D Heterogeneous Grid Based on Linear Interpolation Function

LIU Gang1, CHI Cheng1, SUN Lipeng1, MA Yongqiang1, LI Lin2

(1. Hebei Provincial Key Laboratory of Power Transmission Equipment Security Defense, North China Electric Power University, Baoding 071003， China; 2. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources， North China Electric Power University, Beijing 102206, China)

In the simulation of the multi-physics coupling, since there is a great discrepancy between the requirements of different physical fields on the mesh type and density of the grid, it is normal to use different meshes in different physical fields. In this paper, the method based on linear interpolation function is proposed to solve the problem of data transfer during the simulation of the two-dimensional multi-physics coupling. This paper also puts forward an inverse distance weighted algorithm which is used for the situation that the interpolated nodes are not in any triangle. What’s more, the influence of the mesh size on the interpolation accuracy is analyzed, and the linear interpolation function is validated while grid data is mapping in two-dimensional models. Finally, the temperature of the end winding on the valve side of a ±500kV converter transformer is mapped to the electric field simulation model by using the proposed algorithm, which lays the foundation for studying the two-dimensional hybrid electric field under the condition of non-uniform temperature distribution.

heterogeneous grid; triangular meshing; linear interpolation; multi-physics coupling

2017-04-06.

国家自然科学基金资助项目(51407075)；河北省自然科学基金项目(E2015502004);中央高校基本科研业务费专项资金资助项目(2015MS79).

10.3969/j.ISSN.1007-2691.2017.06.02

TM401

A

1007-2691(2017)06-0008-06

刘 刚(1985-)，男，讲师，硕士生导师，主要研究方向为电气设备多物理场建模及仿真;池骋(1992-)，女，硕士研究生，研究方向为电磁场理论及其应用，电气设备多物理场建模及仿真;孙立鹏(1993-)，男，硕士研究生，研究方向为电磁场理论及其应用，电气设备多物理场建模及仿真;马永强(1993-)，男，硕士研究生，研究方向为电磁场理论及其应用，电气设备多物理场建模及仿真;李琳(1962-)，男，教授，博士生导师，研究方向为电力系统电磁兼容、无线电能传输技术。