永磁同步电机新型转矩自适应控制

郑晓明， 米增强， 魏明磊， 李晓龙， 孙辰军

(1.华北电力大学 电气与电子工程学院，河北 保定 071003; 2. 国网河北省电力公司，河北 石家庄 050022)

永磁同步电机新型转矩自适应控制

郑晓明1， 米增强1， 魏明磊2， 李晓龙2， 孙辰军2

(1.华北电力大学 电气与电子工程学院，河北 保定 071003; 2. 国网河北省电力公司，河北 石家庄 050022)

在很多场合永磁同步电机的输出转矩需要精确控制，同时希望转速平稳，不受电机参数变化及负载扰动的影响。介绍了一种以转速、转矩和磁链为虚拟变量的反推控制算法，可以使永磁同步电机的输出转矩在全局范围内快速无差跟踪负载转矩，并结合自适应控制律，可以实时估计定子电阻和负载转矩，能有效减小内外部扰动对电机转速的影响。仿真结果表明：此控制方法可以有效提高系统的静态和动态性能，保证系统的全局收敛，且转矩跟踪迅速，电机参数变化和负载扰动对电机转速的影响很小，有良好的伺服性能和较强的抗干扰能力。

永磁同步电机； 反推控制； 虚拟变量； 自适应律

0 引 言

近年来永磁同步电动机(permanent magnet synchronous motors,PMSM)在越来越多的场合得到应用。与感应电机和直流电机相比，PMSM具有高转矩体积比、高转矩电流比、效率高、机械结构简单的优点[1-2]。但是由于PMSM参数间的非线性耦合，一般的线性控制方法难以实现控制性能的要求，而且在PMSM的运行过程中，定子电阻会随着PMSM的持续运行而温度升高，阻值会随之变大[3]，除此之外，负载转矩也可能会发生变化，这些内外部参数的变化会影响到电机转速的稳定性，转矩的精确性。考虑到一些场合要求PMSM输出转矩有精确快速的跟踪能力[4]，且转速平稳，达到这样的要求需要控制系统有很强的鲁棒性，一般的线性控制方法很难实现，当前的非线性控制方法主要有滑模控制[5]、神经网络控制[6]、模糊控制[7-8]等，但这些方法设计过程比较复杂，一般难以实现。

反推控制是一种非线性控制方法[9]，越来越多的应用于PMSM调速控制领域[10]，其通过选择虚拟控制变量和构建合适的李雅普诺夫函数把PMSM的控制模型分解成若干个子系统，在实现PMSM完全解耦的同时也使控制器设计更加简单。文献[11]将反推控制用于PMSM的速度跟踪控制中，文献[12]结合反推控制和模糊控制用于PMSM的位置跟踪控制中，文献[13-14]将反推控制用于永磁同步电机位置跟踪控制中，文献[15]引入了Luenberger观测器，设计了PMSM无速度传感器反推控制算法，文献[16]加入了转矩和定子电阻自适应控制律，使控制系统有更强的鲁棒性。但上述方法在设计控制器时均采用转角、转速、d-q轴电流为虚拟控制变量，对转矩是否能精确跟踪并未提及，设计李雅普诺夫函数的时候也没有考虑，虽然对于表面式永磁同步电机而言，q轴电流与输出转矩直接相关，但毕竟同时受到其它参数的影响，假如这些参数发生偏移，这无疑会影响PMSM输出转矩的精度。本文提出了一种新型PMSM反推自适应控制系统，以转速、转矩和磁链为虚拟控制变量，分别设计转速、转矩和磁链反推控制器，根据李雅普诺夫定理分析可得，控制系统能同时保证PMSM转速和转矩的全局收敛和准确跟踪，同时加入了定子电阻和负载转矩自适应控制器，能有效减小内外扰动对转速和转矩的影响，在负载转矩和转速同时需要精确跟踪的场合有一定的意义。

1 永磁同步电机模型

表面式PMSM(交直轴电感相等，即Ld=Lq=L)在同步旋转坐标系下的模型如下：

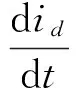
(1)

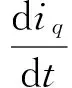
(2)

ψd=ψf+Lid

(3)

ψq=Liq

(4)

Te=1.5npψfiq

(5)

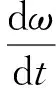
(6)

(7)

式中：ud，uq分别为定子d，q轴电压；id，iq分别为定子d，q轴电流；R为定子电阻；L为定子电感；np为极对数；ω为电动机旋转角速度；ψf为转子磁链；ψd，ψq分别为定子磁链在d，q轴的分量；TL为负载转矩；Te为电磁转矩；J为转子的转动惯量；B为粘性摩擦系数；定义ψs为ψd和ψq的平方和。

2 自适应控制器设计

反推控制是一种非线性递推算法，其设计过程是从控制系统的模型出发，利用虚拟控制变量使高阶非线性系统逐步简化，并通过设计李雅普诺夫函数在保证系统全局收敛的同时得到最终实际控制变量。

2.1 转速控制器设计

假定转速参考值ωref恒定，跟踪误差为

eω=ωref-ω

(8)

选择eω为虚拟控制变量，构成子系统，对eω求导可得：

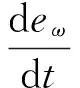
(9)

为了使转速误差在全局范围内快速收敛，选择Te为虚拟控制变量，构造李雅普诺夫函数函数：

(10)

对上式求导可得：

(11)

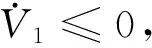
Teref=Bω+TL+k1Jeω

(12)

其中k1>0，带入式(11)可得：

(13)

可知转速能实现全局渐进跟踪。

在实际的PMSM控制系统中，定子电阻R会受到温度的影响，并在负载转矩TL也可能存在实时的扰动，偏离标称值，令：

(14)

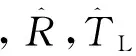
(15)

将式(15)带入式(11)可得：

(16)

2.2 转矩控制器设计

为了实现PMSM转矩能快速跟踪负载转矩，建立如下误差函数：

(17)

对其求导，并且把定子电阻R和负载转矩TL的标称值用实际值和误差值代替，可得：

(18)

(19)

求导可得：

(20)

uq为实际控制变量，为控制器的输入信号：

(21)

其中k2>0，将式(21)带入式(18)，并将其结果带入式(20)可得：

(22)

2.3 磁链控制器设计

定义磁链误差函数如下：

eψ=ψsref-ψs

(23)

对误差变量求导，并且把定子电阻R和负载转矩TL的标称值用实际值和误差值代替，可得：

(24)

设计李雅普诺夫函数如下：

1．对创新创业教育的认识有偏差。创新创业教育的核心和本质是面向全体学生的、为其终身可持续发展奠定基础的素质教育。［6］创新创业教育是“完人”教育、培养开创性的教育，而非提高就业率的“缓兵之计”，更非创收的”孵化器”，不能简单地计算学生参加了多少创新创业活动，从事了多少创业项目，获取了多少创业资金。［6］创新创业教育的实质是素质教育，不能仅限于技能教育、技术教育、就业能力教育。只有认识到创新创业教育的本质特点，才能从总体上把握全局，定好创新创业的主基调，注重开发学生的思维能力。

(25)

求导可得：

(26)

ud为实际控制变量，为控制器的输入信号：

(27)

其中k3>0，将式(21)、(27)带入式(24)，并将其结果带入式(26)可得：

(28)

2.4 自适应控制律设计

为了加强控制系统对定子电阻和负载转矩的抗扰动性能，设计李雅普诺夫函数如下，其中r1>0，r2>0：

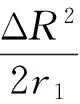
(29)

求导可得：

(30)

设计自适应控制律如下：

(31)

(32)

将式(31)、(32)代入式(30)可得：

(33)

由于V4有界，根据Barbalat推论，可得：

(34)

即控制系统误差变量eω、eT、eψ在全局范围内收于零，在系统存在内外部扰动的情况下，能同时保证转速，转矩和磁链的精确跟踪。

3 仿真结果分析

基于以上分析，控制系统框图如图1所示。在Matlab软件中编写了程序并进行了仿真分析。仿真中PMSM参数选取如下：永磁体磁通ψf=0.8 Wb，交直轴等效电感L=0.033 H，极对数np=10，定子电阻R=2.875 Ω，粘滞系数B=0.002，B=0.001 N/r/s，J=0.51 kg·m2。控制器参数选取如下：k1=0.1，k2=320.7，k3=1444.2，r1=4.529，r2=1 853.75，仿真步长设置为0.000 1 s，仿真时间为10 s。

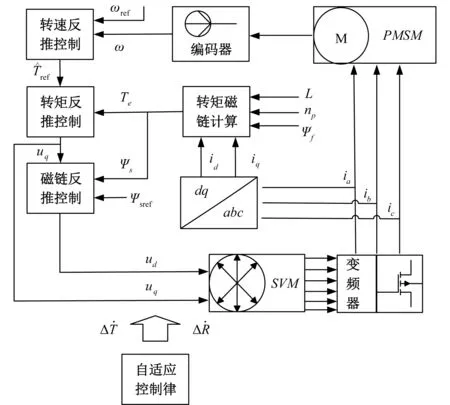
图1 控制系统框图Fig.1 Diagram of control system

本文根据是否加自适应环节进行了两组仿真，两组仿真的指令是一致的，PMSM转速指令为：在0～2 s为2r/s，在2～3 s为3r/s，在3～10 s为2r/s；负载转矩指令为：在0～4 s为100 N·m，在4～5 s为120 N·m，在5～10 s为100 N·m；定子电阻指令为：在0～7.5 s为2.875 Ω，在7.5～10 s增加20%。图2～3为不加自适应控制环节PMSM转速和输出转矩响应波形，图4～5为加自适应控制环节PMSM转速和输出转矩响应波形。

3.1 无自适应控制仿真分析

分析图2可得：PMSM转速在启动后约0.2 s到达指定转速，在2 s、3s处转速指令突变，PMSM转速能无差跟踪，但响应较慢，在4 s处负载转矩突增，PMSM转速有一个减速再恢复到指令值的过程，在5 s处负载转矩突减，PMSM转速有一个加速再恢复到指令值的过程，虽然最终均能回到指令值，但恢复时间较长，且动态尖峰较大，在7.5 s处定子电阻突增20%，PMSM转速跟踪误差加大。

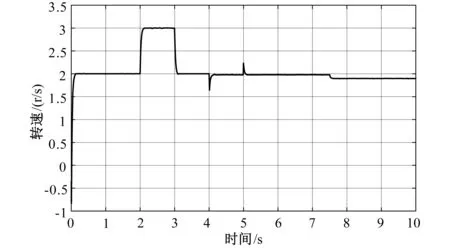
图2 转速响应曲线Fig.2 Speed response curve

图3 电机输出转矩响应曲线Fig.3 Torque response curve of PMSM

分析图3可得：PMSM转矩在启动后约0.2 s达到负载转矩，但有一定的超调，约为稳态值的50%，在2 s、3s处转速指令突变，PMSM转矩对应有一个向上和向下的尖峰，约为稳态值的20%，虽然最终能恢复到稳态值，但响应时间较长，在4 s、5s处负载转矩突变，PMSM输出转矩能有效跟踪，但有一定的超调，且存在一些抖震，在7.5 s处定子电阻突增20%，PMSM输出转矩有一个尖峰。

3.2 自适应控制仿真分析

分析图4可得：PMSM转速在启动后约0.1 s到达指定转速，在2 s、3s处转速指令突变，PMSM转速能无差跟踪，超调较小，且响应很快，在4 s处负载转矩突增，在5 s处负载转矩突减，PMSM转速有一个很小的抖动便迅速恢复到指定值，在7.5 s处定子电阻突增20%，PMSM转速能较快响应且无差跟踪。

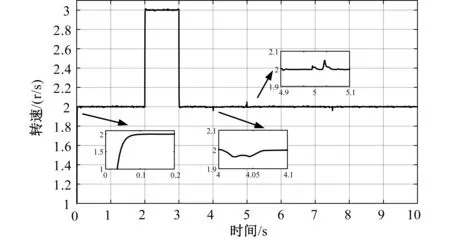
图4 转速响应曲线Fig.4 Speed response curve

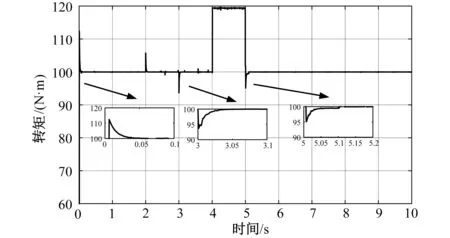
图5 电机输出转矩响应曲线Fig.5 Torque response curve of PMSM

分析图5可得：PMSM转矩在启动后约0.05 s达到负载转矩，超调约为15%，在2 s、3s处转速指令突变，PMSM转矩对应有一个向上和向下的尖峰，约为稳态值的5%，很快恢复到稳态值，在4 s、5s处负载转矩突变，PMSM输出转矩能有效跟踪，超调很小，在7.5 s处定子电阻突增20%，PMSM输出转矩基本看不到变化，转矩输出平稳精确。

4 结 论

本文介绍了一种以依次以转速、转矩、磁链为虚拟控制变量的PMSM反推控制方法，并且加入了定子电阻和负载转矩自适应控制器，通过对比两组Matlab仿真分析结果可知：本文所提的方法能同时保证PMSM转速和转矩的精确跟踪和快速响应，并且能有效抑制参数变化对PMSM转速和输出转矩的影响，系统有很强的鲁棒性和良好的伺服性能。

[1] GÜEMES J A, IRAOLAGOITIA A M, HOYO J I D, et al. Torque analysis in permanent-magnet synchronous motors: a comparative study[J]. IEEE Transactions on Energy Conversion, 2011, 26(1):55-63.

[2] MORAWIEC M. The adaptive backstepping control of permanent magnet synchronous motor supplied by current source inverter[J]. IEEE Transactions on Industrial Informatics, 2013, 9(2):1047-1055.

[3] 冯文轶, 陈剑, 张宇宁. 基于电阻辨识自传感技术的永磁同步电动机温度检测[J]. 微特电机, 2014, 42(8):55-58.

[4] 米增强, 余洋, 王璋奇,等. 永磁电机式机械弹性储能机组及其关键技术初探[J]. 电力系统自动化, 2013, 37(1):26-30.

[5] 米李政, 胡广大, 崔家瑞,等. 永磁同步电机调速系统的积分型滑模变结构控制[J]. 中国电机工程学报, 2014, 34(3):431-437.

[6] 谷鑫, 胡升, 史婷娜,等. 基于神经网络的永磁同步电机多参数解耦在线辨识[J]. 电工技术学报, 2015, 30(6):114-121.

[7] 梁新涛. 基于模糊控制的永磁同步电机控制研究[J]. 现代制造, 2014，(33):114-116.

[8] 邹权, 钱林方, 蒋清山. 永磁同步电机伺服系统的自适应模糊滑模控制[J]. 控制理论与应用, 2015, 32(6):817-822.

[9] YANG J H, WU J, HU Y M. Backstepping method and its applications to nonlinear robust control[J]. Control & Decision, 2002，(Suppl):641-647.

[10] KARABACAK M, ESKIKURT H I. Design, modelling and simulation of a new nonlinear and full adaptive backstepping speed tracking controller for uncertain PMSM[J]. Applied Mathematical Modelling, 2012, 36(11): 5199-5213.

[11] 王家军, 赵光宙, 齐冬莲. 反推式控制在永磁同步电动机速度跟踪控制中的应用[J]. 中国电机工程学报, 2004, 24(8):95-98.

[12] 于金鹏, 陈兵, 于海生,等. 基于自适应模糊反步法的永磁同步电机位置跟踪控制[J]. 控制与决策, 2010, 25(10):1547-1551.

[13] 王家军,赵光宙,齐冬莲，等.基于反推的永磁同步电动机伺服系统的位置跟踪控制[J].电路与系统学报,2004,9(6):19-21.

[14] 王家军. 速度指定位置跟踪双永磁同步电动机的反推控制[J]. 控制理论与应用, 2015, 32(2):202-209.

[15] 刘栋良, 郑谢辉, 崔丽丽. 无速度传感器永磁同步电机反推控制[J].电工技术学报, 2011, 26(9):67-72.

[16] 刘栋良, 王家军, 崔丽丽. 永磁同步电机参数自适应调速控制[J]. 电工技术学报, 2011，26(8):159-165.

A New Torque Adaptive Control of PMSM

ZHENG Xiaoming1, MI Zengqiang1,WEI Minglei2,LI Xiaolong2,SUN Chenjun2

(1. School of Electrical and Electronic Engineering,North China Electric Power University, Baoding 071003,China; 2. State Grid Hebei Electric Power Company, Shijiazhuang 050022, China)

The output torque of permanent magnet synchronous motors (PMSM) needs precise control and steady speed but without being affected by the variation of motor parameter and load disturbance on many occasions. This paper introduces a back-stepping control algorithm regarding speed, torque and flux linkage as virtual control variable to realize the rapid trace to the output torque on a global scope and to diminish the impact of disturbance on the speed by estimating the resistance and load torque with the combination of adaptive control law. The simulation result demonstrates that the control method can improve the static and dynamic performances and guarantee the global convergence of system. Besides, with the rapid torque tracking and negligible influence by the variation of motor parameter and load disturbance, the system possesses good servo performances and anti-disturbance performances.

PMSM; back-stepping control; dummy variable; adaptive law

2017-04-13.

中央高校基本科研业务费专项资金资助项目(2016XS96)；新能源电力系统国家重点实验室自主研究课题(LAPS2016-28)；国家电网公司2016年总部科技项目(5204BB16000F).

10.3969/j.ISSN.1007-2691.2017.06.06

TM351

A

1007-2691(2017)06-0036-05

郑晓明(1986-)，男，博士研究生，研究方向为机械弹性储能技术与永磁同步电机控制；米增强(1960-)，男，教授，博士生导师，主要研究方向为新能源电力系统与智能电网，机械弹性储能技术。