近几年中考数学(北京卷)几何综合题综述
王亮亮
(北京教育考试院 100083)
1 引言
北京中考数学几何综合题向来以创新和难度著称,一直引起广大师生的关注.一方面,试题对考生的几何基础、推理能力、抽象能力和论证能力等方面具有很高的要求;另一方面,试题背景新颖、内涵丰富思想深刻、方法质朴,对考生具有很好的区分功能.同时,也为初中数学教学指明了方向.但通过调研听课发现,由于试题的难度较大,很多教师在讲解时遇到了一些困难,如试题的内涵阐述不全面等.本文将以2012,2014,2015年几何综合题为例,对近六年的几何综合题做一次总结,与大家分享试题背后的思想和试题对教学的引导作用,希望能给一线教师提供一点经验.
2 2012,2014,2015年试题呈现
2012年在△ABC中,BA=BC,∠BAC=α,M是AC的中点,P是线段BM上的动点,将线段PA绕点P顺时针旋转2α得到线段PQ.
(1)若α=60°且点P与点M重合(如图1),线段CQ的延长线交射线BM于点D,请补全图形,并写出∠CDB的度数;
(2)在图2中,点P不与点B,M重合,线段CQ的延长线与射线BM交于点D,猜想∠CDB的大小(用含α的代数式表示),并加以证明;
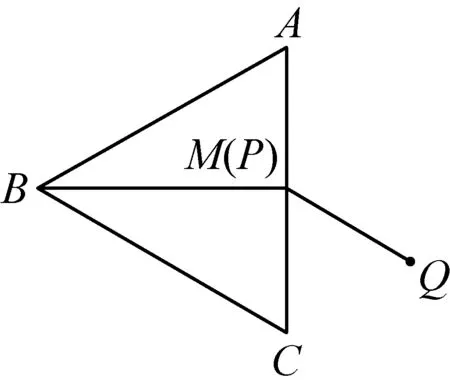
图1
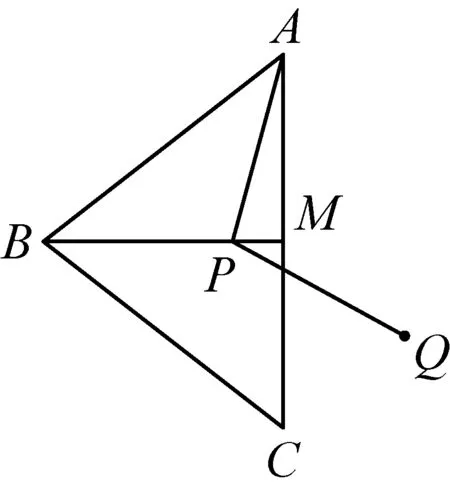
图2
(3)对于适当大小的α,当点P在线段BM上运动到某一位置(不与点B,M重合)时,能使得线段CQ的延长线与射线BM交于点D,且PQ=QD,请直接写出α的范围.
2014年在正方形ABCD外侧作直线AP,点B关于直线AP的对称点为E,连接BE,DE,其中DE交直线AP于点F.
(1)依题意补全图1;
(2)若∠PAB=20°,求∠ADF的度数;
(3)如图2, 若45°<∠PAB<90°,用等式表示线段AB,FE,FD之间的数量关系,并证明.
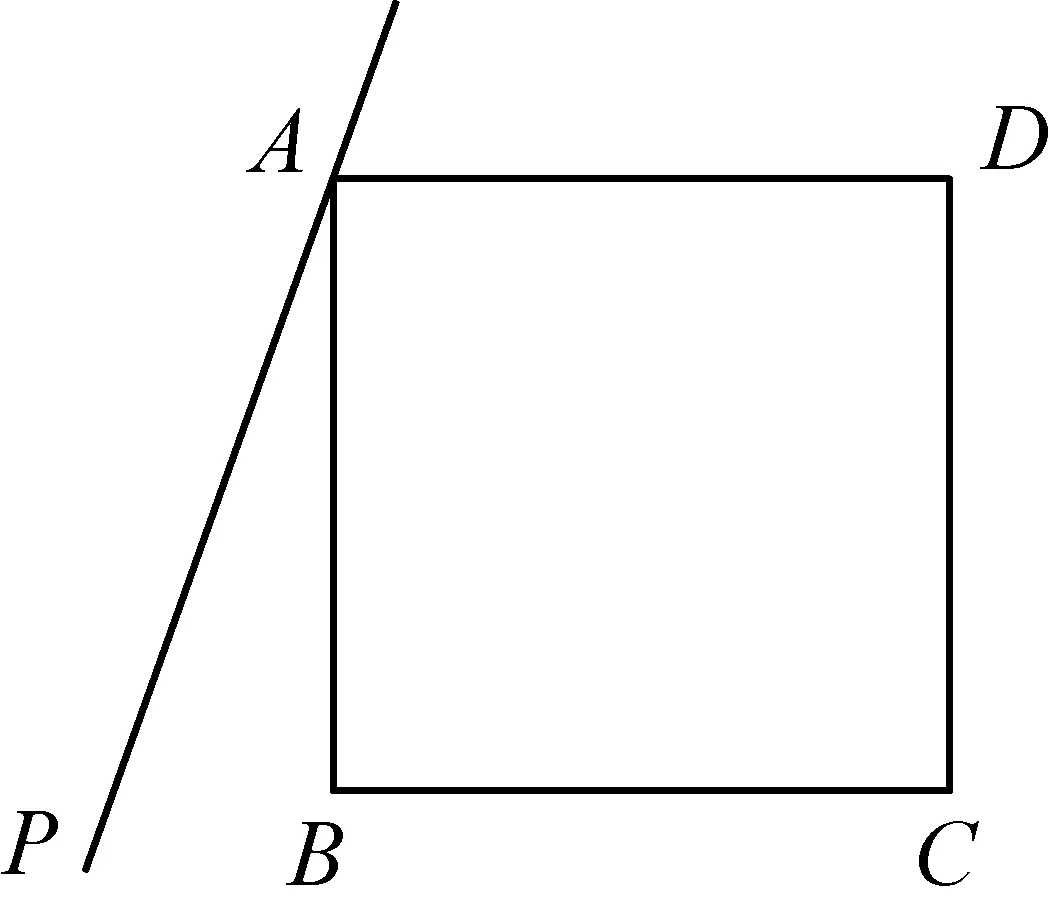
图1
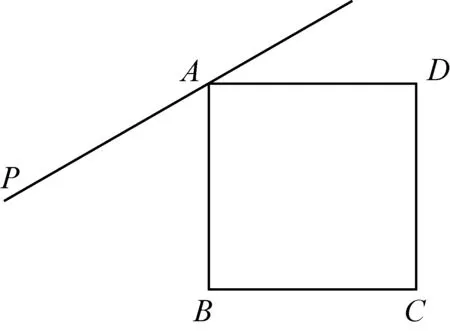
图2
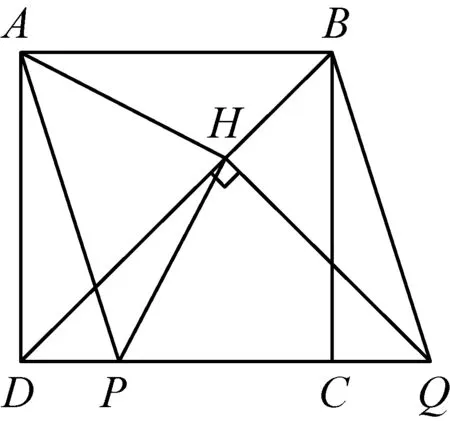
2015年在正方形ABCD中,BD是一条对角线.点P在射线CD上(与点C,D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于点H,连接AH,PH.
(1)若点P在线段CD上,如图1,
①依题意补全图1;
②判断AH与PH的数量关系与位置关系并加以证明;
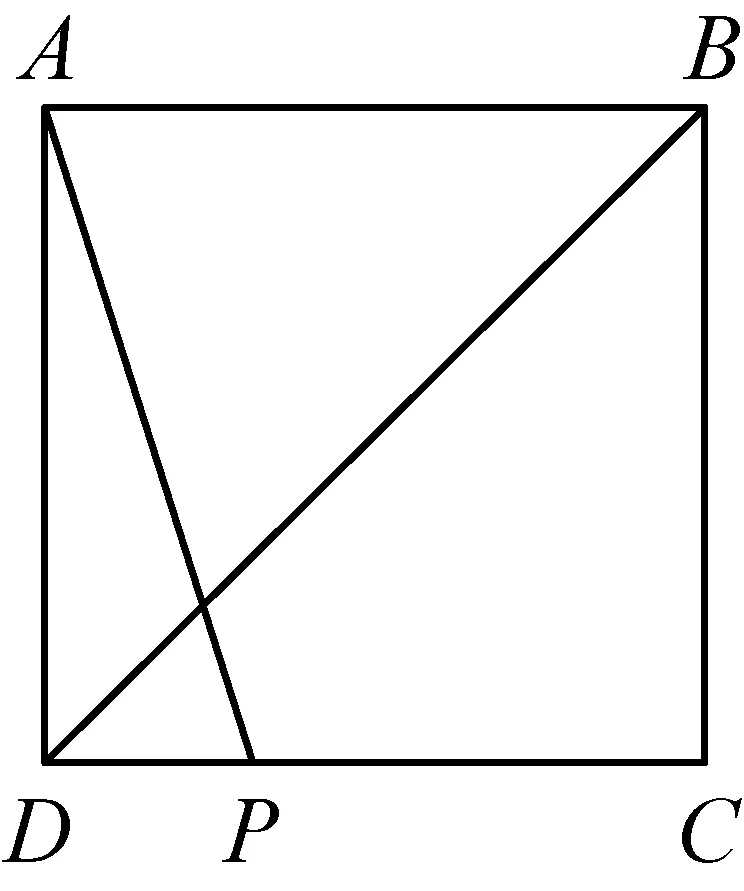
图1

图2
(2)若点P在线段CD的延长线上,且∠AHQ= 152°,正方形ABCD的边长为1,请写出求DP长的思路.(可以不写出计算结果)
3 试题综述
3.1 通过画图,抽象思维化为形象思维,发现解决问题思路
对于画图的要求,这是培养学生几何直观能力的基础.因为在画图的过程中,可以使学生体会到画图对于理解概念、寻求解题思路带来的益处.更重要的是,逻辑证明的过程、形式化的结论都是在形象思维的基础上产生的,这是画图作为几何直观能力基础的核心要义.
2012、2014、2015年试题的第(1)问都是要求学生补全图形.补全图形的过程,其实质就是将抽象的语言和研究对象“图形化”,把需要解决的问题、证明等数学过程变的更加直观,有助于进行具体的操作,并在此基础上有助于发现研究问题的思路.下面以2012(1)、2014(1)和2015(1)为例说明.

2012(1)
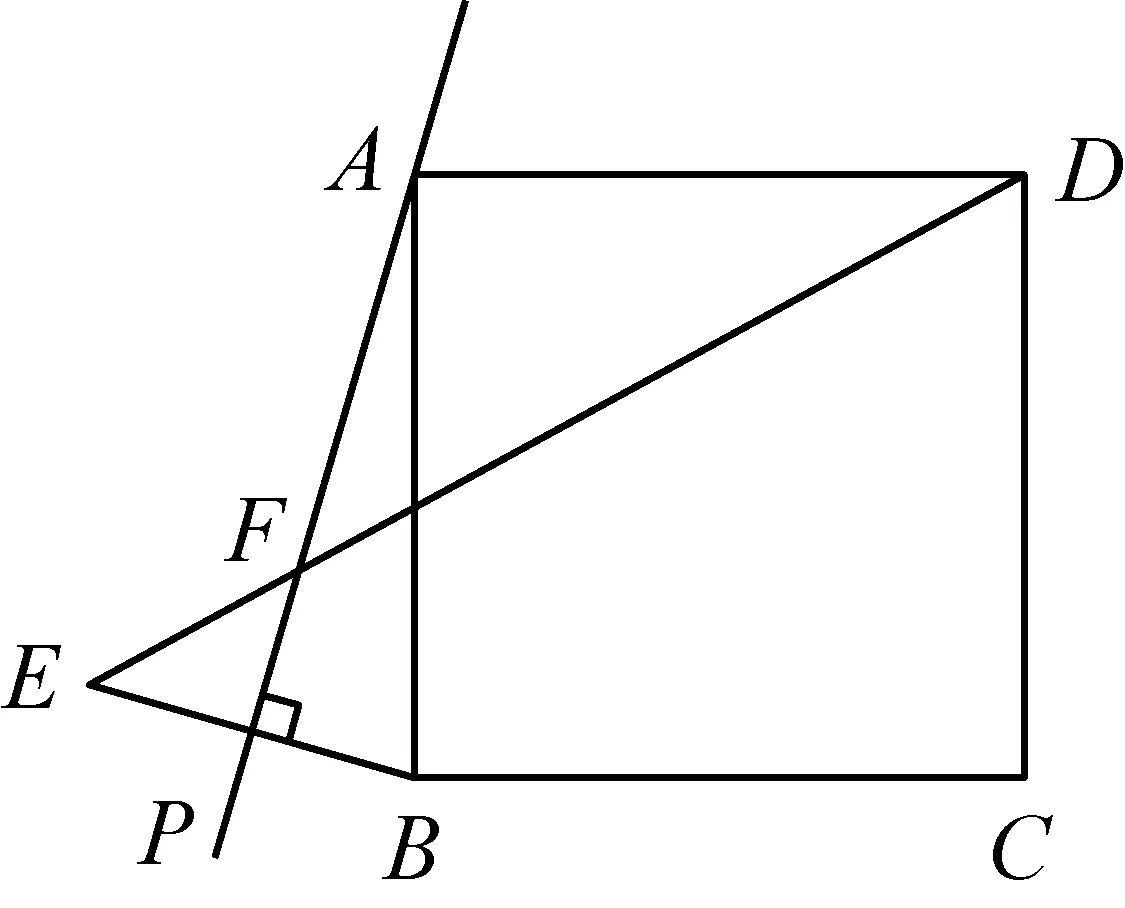
2014(1)
2015(1)
如2012(1),补全图形后发现,BD是△ABC的对称轴,△CQM是在旋转与轴对称变换基础上形成的等边三角形等,这就为问题的解决提供了明确的思路——利用轴对称和旋转变换的性质研究图形.又如2014(1),通过补全图形体会到AP是线段BE的垂直平分线,通过这一性质可以发现后面问题研究的角度——轴对称变换分析图形.再如2015(1),补全图形后发现△BCQ是由△ADP平移得来的,可以根据平移的性质探索研究问题的思路.
3.2 重视几何变换,将变换性质作为解决问题的桥梁
几何变换是几何体系的核心内容,几何变换可以看作是图形运动,它是认识图形的基本方法,也是认识数学思想和方法的基本途径.通过运动变化理解轴对称、旋转和平移变换的基本性质,可以抽象出图形运动变化过程中的不变量和不变关系,从而为运用图形运动的方法研究图形的性质奠定基础,使其成为研究图形的桥梁.2012(2)、2014(3)、2015(1)都以几何变换的性质为桥梁解决问题,下面以2012(2)和2014(3)为例说明.
2012(2)以轴对称和旋转变换为基础.在第(1)问补全图形的基础之上,根据BA=BC,M是AC的中点,可推导出BD是△ABC的对称轴.根据轴对称的性质,可以连接PC和AD,进一步推导出BD是四边形ABCD的对称轴,所要求的∠BDC就转化成了求∠ADC.再根据旋转的性质,可以推导出△PCQ是等腰三角形,进而问题可求.问题的解决是以轴对称和旋转变换的基本性质为基础的,让问题的解决更加直观、思考问题的方向更加明确.

2012(2)
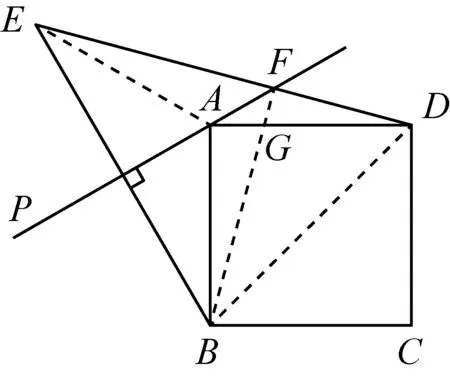
2014(4)
2014(3)以轴对称变换为基础解决线段AB,FE,FD之间的数量关系.在第(1)问补全图形的基础之上,可知对图形进行的是轴对称变换的操作.根据轴对称的性质,可以连接AE和FB,需要解决的线段AB,FE,FD之间的数量关系就转化成为了FB,FD,AB的数量关系.通过对图形的进一步分析可以发现,上述三条线段可以放到Rt△BFD中,即只需证明∠BFD=90°,而证明∠BFD=90°的核心思想也是利用轴对称的性质推导出∠ABF=∠DEA=∠ADE.问题的解决是在轴对称性质的基础之上,不断发现解决问题思路.
3.3 重视演绎推理,更加注重有条理表述思考过程
传统上对于推理能力的培养,往往被认为是加强逻辑证明的训练,主要的形式就是通过习题演练以掌握更多的证明技巧.这样的认识是有局限性的.让学生经历从特定对象的本质属性入手,抽象、概括形成概念的过程,引导学生有条理地表述概念定义,引导学生分清条件、结论,把握条件、结论间的逻辑关系,让学生遵循证明规则,通过数学推理、证明数学结论……,这些方面都是推理能力的表现形式.
2015年第(2)问设问的方式就是基于上述表现形式的思考进行了一定的突破.写思路的立足点是让学生有条理的表述自己的思考过程,它的前提条件是“会做”此题.在“会做”的基础上,学生能根据条件和结论间的逻辑关系,阐述所解决问题之间的联系与区别,表达解决问题的思路.
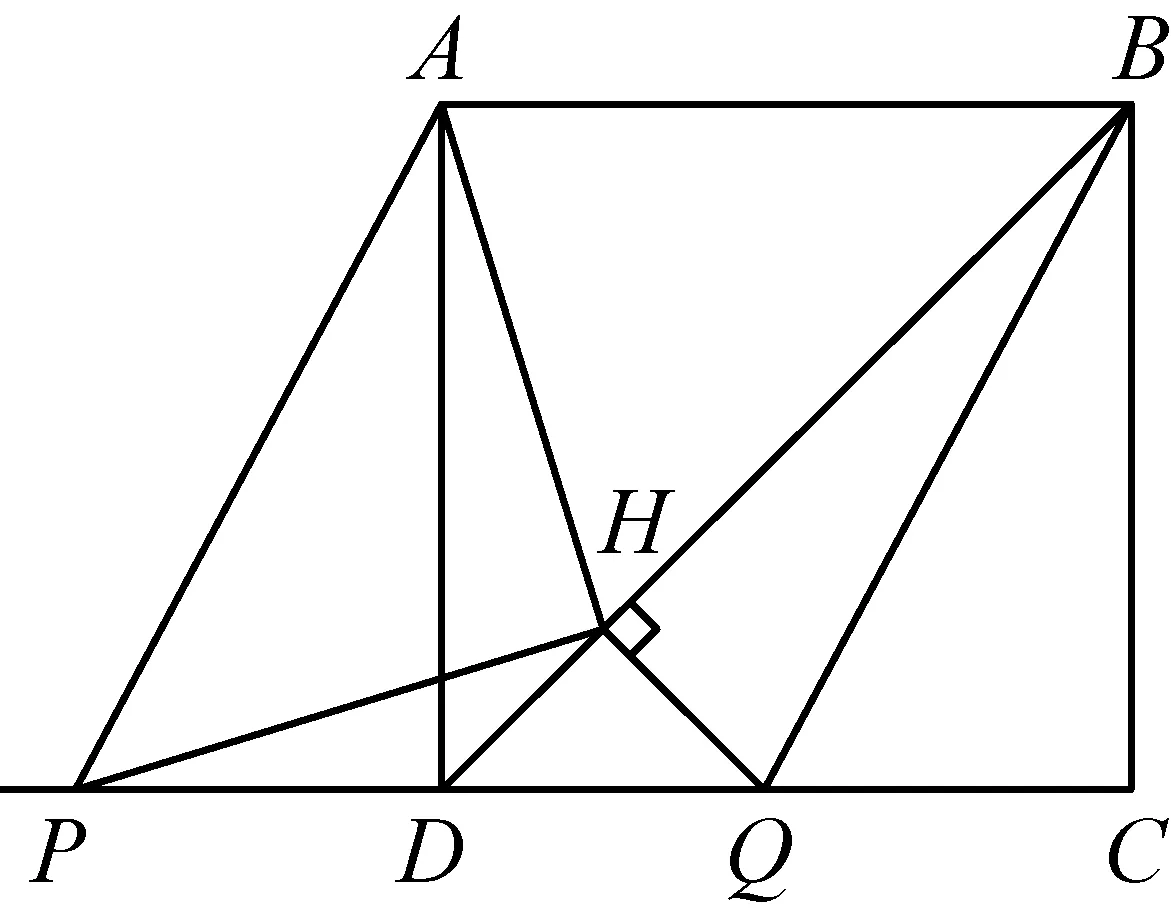
2015(2)
通过分析可以发现,问题解决的核心是证明出△APH是等腰直角三角形.对两问的条件与结论进一步对比分析可知,证明AH=PH的过程是一模一样的,所以对这一相同过程可以用“与②同理,可证△AHD≌ △PHQ,可得AH=PH”来阐述 .而对∠AHP=90°证明过程的分析发现,在(1)②中是∠AHD+∠PHD,(2)中是∠AHD-∠PHD,所以在阐述这一区别时应该明确指出其推导过程“由∠AHP= ∠AHD-∠PHD=∠PHQ-∠PHD= 90°,可得△AHP是等腰直角三角形”.
对上面写思路过程的分析发现,有条理的表述思考过程的要求是证明过程的一种思维升华,它不仅仅要求学生“会做”题目,还要求学生能把题目的逻辑结构想明白、阐述清楚.
4 思考
4.1 几何直观能力与逻辑推理能力应并重
几何教学中偏向于逻辑推理能力的培养,忽略了几何直观能力的培养.正如试题描述中的阐述,图形有助于发现、描述问题,有助于探索、发现解决问题的思路,也有助于理解结论.图形可以把复杂的数学问题变得简洁、明了,学会用图形思考数学问题,也是数学学习能力的体现.
4.2 逻辑推理能力要落在思考过程中,而不是证明技巧中
推理能力的培养不能片面的认为是通过习题演练掌握更多的技巧,而是在过程中去逻辑性思考问题,有机的把握条件、结论间的逻辑关系,对问题的结构能有效的进行阐述,在过程中感悟逻辑思考的思维方式.
4.3 几何变换为桥梁,让图形运动起来,感受直观,培养理性
几何直观与逻辑推理是密不可分的.几何直观常常是靠逻辑来支撑的,不仅是看到了什么,而是通过看到的图形思考到了什么,这是非常重要的数学思考方式.通过思考,可以想象出一些可能点的结果或思路.利用几何变换这一桥梁,通过几何变换的基本性质研究、推导出图形的性质,不仅能对图形的本质进行认识,同时也是对几何直观的一种提升.它们是相辅相成,密切联系在一起的.
5 总结
本文以2012,2014,2015中考数学(北京卷)几何综合题为例,阐述了近几年几何综合题的发展趋势、主要特点和几点思考,主要是想交流一下题目背后的思想和对教学的引导作用,如有不当之处请批评指正.

