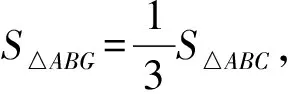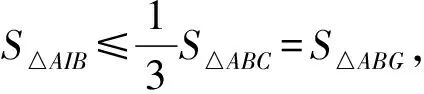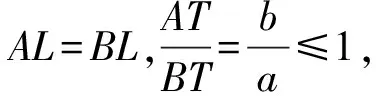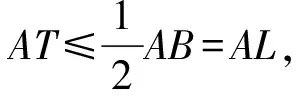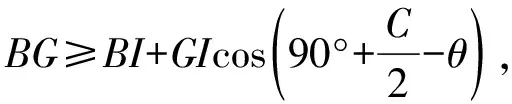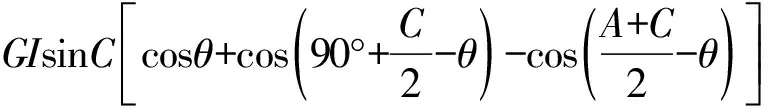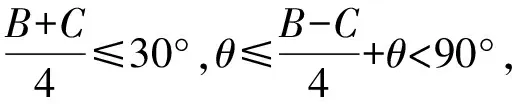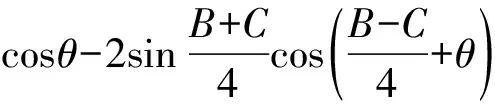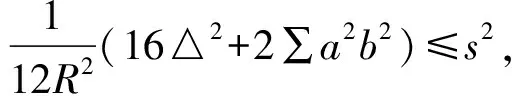锐角三角形四心垂足三角形的周长不等式链

胡文生

(江西省九江市德安磨溪中学)

文[1]给出了“四心垂足三角形面积的一条不等式链”，人们自然而然地会想到，四心垂足三角形是否存在一条周长不等式链呢？经笔者研究发现，答案是肯定的.

在锐角三角形ABC中,H,I,G,O分别为垂心，内心，重心，外心；分别过H,I,G,O作BC,CA,AB的垂线，垂足分别为A1,B1,C1,A2,B2,C2,A3,B3,C3,A4,B4,C4，则△A1B1C1，△A2B2C2，△A3B3C3，△A4B4C4分别为△ABC的垂心，内心，重心，外心的垂足三角形，设它们的周长分别为S1,S2,S3,S4，△ABC的面积，半周长，和外接圆、内切圆半径分别为△,s,R,r，对四心垂足三角形的周长间的关系同样有如下一个有趣的结论：

定理S1≤S2≤S3≤S4=s

(*)

证明如图1，H是△ABC的垂心，三角形三边三内角分别为a,b,c,A,B,C,AA1,BB1,CC1是三条高，△A1B1C1是垂心垂足三角形，记

B1C1=a1,C1A1=b1,A1B1=c1.

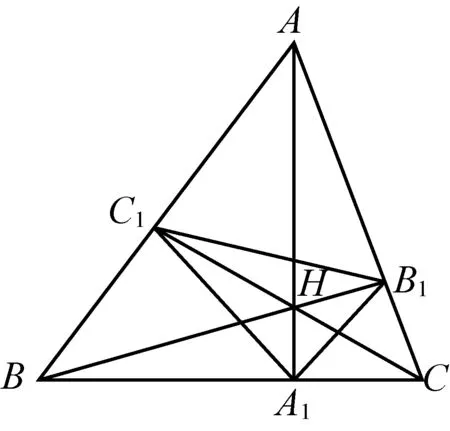
图1

因为Rt△AHB1∽Rt△ACA1,

由图1知A1C=bcosC，AB1=ccosA，

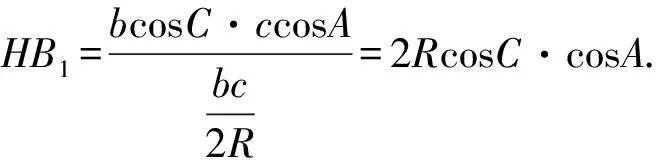
同理HC1=2RcosAcosB，

HA1=2RcosBcosC.

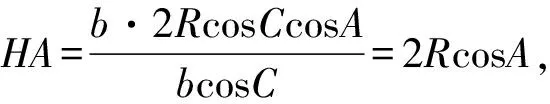
同理HB=2RcosB，HC=2RcosC.

因为HA是△HB1C1外接圆直径，设它的半径为R′，由正弦定理知

a1=B1C1=2R′·sin∠C1HB1=HA·sinA

=2RcosA·sinA=Rsin2A

同理b1=C1A1=Rsin2B，

c1=A1B1=Rsin2C.

所以△A1B1C1的周长为

S1=a1+b1+c1=R(sin2A+sin2B+sin2C)

=4RsinAsinBsinC

(1)

如图2，I是△ABC的内心，A2,B2,C2是切点，△A2B2C2是内心垂足三角形,

图2

且IA2=IB2=IC2=r，

记B2C2=a2,C2A2=b2,A2B2=c2，

因为IA是△IB2C2外接圆直径，设它的半径为R″，由正弦定理知

a2=B2C2=2R″sin∠C2IB2=IAsinA

所以△A2B2C2的周长为

(2)

或

S2=a2+b2+c2=IAsinA+IBsinB+ICsinC

(3)

如图3，G是△ABC的重心，GA3,GB3,GC3分别垂直三边，垂足分别为A3,B3,C3,△A3B3C3是重心垂足三角形，记B3C3=a3,C3A3=b3,A3B3=c3，ma,mb,mc是三条中线.

图3

因为GA是△GB3C3外接圆直径，设它的半径为R‴，由正弦定理知

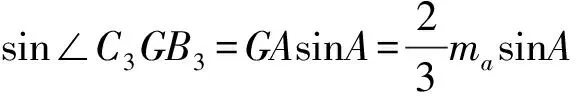
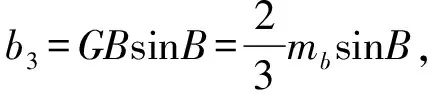
所以△A3B3C3的周长是

S3=a3+b3+c3

(4)

或

S3=a3+b3+c3

=GAsinA+GBsinB+GCsinC

(5)

按不等式链(*)从左到右的顺序，为证(*)式，先证第一个不等式S1≤S2.

由已知恒等式

acosA+bcosB+ccosC=4RsinAsinBsinC

和(1)式及

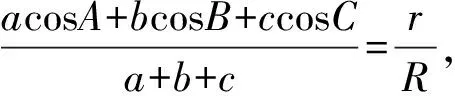
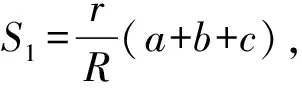
再由(2)式知，欲证S1≤S2，只需证

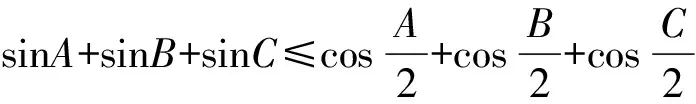
(6)

由恒等式

故(6)式得证，所以有S1≤S2.

下面再证S2≤S3，由(3)、(5)两式知只要证

GAsinA+GBsinB+GCsinC

≥IAsinA+IBsinB+ICsinC

(7)

本文借用书[2]第45页的例5的证明稍加调整和修改即可用来证明(7)式.

如图4，I、G分别是△ABC的内心和重心，设BC=a,AC=b,AB=c，不妨设a≥b≥c，则有sinA≥sinB≥sinC.(注意本文讨论的是锐角三角形)

下面证明G一定落在△BIC内或边界上.

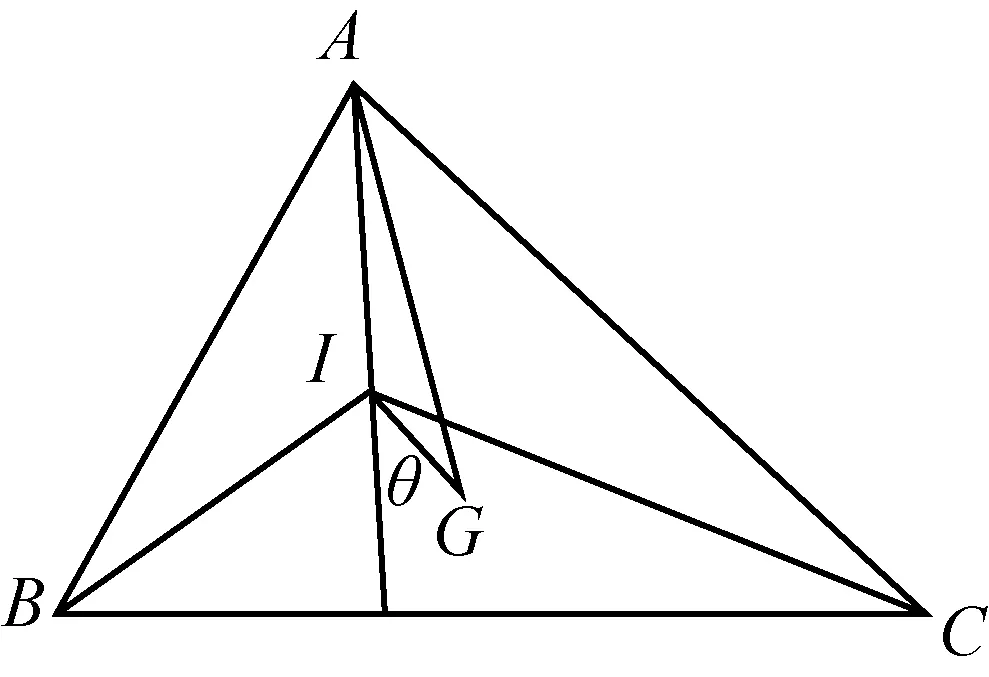
图4

先证G不落在△AIB内，若不然，假设G落在△AIB内，则有S△ABG

因此G落在△BIC内或边界上，且可证G在AI右侧;

由此可知AG≥AI+GIcosθ，

将以上三式两边分别乘以sinA、sinB、sinC得

AGsinA≥(AI+GIcosθ)sinA

①

②

③

由以上①，②，③可得

AGsinA+BGsinB+CGsinC-(AIsinA+

BIsinB+CIsinC)

故GAsinA+GBsinB+GCsinC

≥IAsinA+IBsinB+ICsinC,

即(7)式得证，所以S2≤S3成立.

最后证S3≤S4=s.

因为外心垂足三角形(图略)就是△ABC的三条中位线连结成的三角形，故S4=s，

下面只需证S3≤s

(8)

由(4)式和柯西不等式及三角形中线公式并注意到2∑a2b2-∑a4=16△2得

(9)

(10)

(11)

由书[3]，195页15(1)Goldstone不等式 ∑(ab)2≤4(pR)2(注：式中p即本文的s)知欲证(11)式只需证

即 2s2R2≥8△2=8s2r2⟺R≥2r.

最后一个不等式是著名的欧拉不等式，于是(8)式得证，也就是定理(*)式中右边最后一个不等式得证，从而一条优美而有趣的不等式链(*)式获证. 以上所有不等式当且仅当△ABC为正三角形时等号成立. 证毕.