基于Hellinger距离的判断矩阵排序方法

詹婉荣， 于 海

(洛阳师范学院数学科学学院, 河南洛阳 471934)

基于Hellinger距离的判断矩阵排序方法

詹婉荣， 于 海

(洛阳师范学院数学科学学院, 河南洛阳 471934)

本文基于Hellinger距离提出了一种判断矩阵排序方法， 并研究了该排序方法的保序性、 置换不变性、 相容性等性质.最后通过实例将基于Hellinger距离的排序方法与特征向量法、 和积法以及方根法进行比较， 理论分析和数值结果均表明该方法是有效的.

层次分析法；判断矩阵；Hellinger距离；排序方法

层次分析法(AHP)是系统分析与决策中的一种有效的综合评价方法[1-6].这种方法能够统一处理决策中的定性和定量因素,具有实用性、 系统性、 简洁性等优点,特别适合在社会经济系统的决策分析中使用.与此同时, 有关层次分析法中的判断矩阵排序理论和方法也在不断发展, 传统的、 单一的特征向量排序方法已不能满足理论的发展和应用的需要， 大量具有良好性能的最优化排序方法不断出现.这些方法大致可分为近似计算和最优化排序两大类.其中和积法和方根法是最常用的两种近似算法. 本文基于Hellinger距离， 提出了一种判断矩阵的排序方法,并从保序性及合理的排序方法应具有的性质等几个方面对该方法进行了讨论.理论分析和仿真结果表明， 它是用于判断矩阵排序的一种好方法.

1 预备知识

1.1 正互反矩阵和排序向量

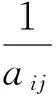
aik·akj=aij,i,k,j=1,2,…,n， 则称A为一致性正互反矩阵.

全体n阶正互反矩阵构成的集合记作Pn, 全体排序向量构成的集合记作Δn， 即

若A为一致性正互反矩阵， 将A归一化后， 列向量均是该判断矩阵的排序向量.然而在实际问题中， 给出的判断矩阵一般不满足一致性条件， 而只能近似满足.层次分析法所要解决的数学问题之一就是， 如何对这样的判断矩阵给出一种近似计算排序向量的方法.在层次分析法中， 用对应判断矩阵的最大特征根的特征向量作为排序向量， 然而计算矩阵的特征根和特征向量是相当困难的， 特别是矩阵的阶数较高的时候.所以计算排序向量可以采用近似算法.目前最常用的近似算法是和积法与方根法.

和积法的计算公式为

方根法的计算公式为

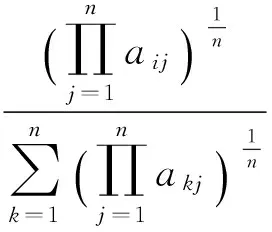
和积法实际上是将判断矩阵A的列向量归一化后取算术平均值， 作为A的排序向量.因为当A为一致阵时， 它的每一列向量都是排序向量. 所以若A的不一致性不严重， 则取A的列向量的算术平均值作为近似排序向量是合理的. 而方根法是对列向量取几何平均值， 再归一化得到的向量作为近似排序向量.

1.2 Hellinger距离定义

在概率论和统计理论中， Hellinger距离被用来度量两个概率分布的相似度[7].

对于连续概率分布， 设f(x)和g(x)分别为两个连续分布P和Q的概率密度函数， 则这两个分布之间的Hellinger距离定义为

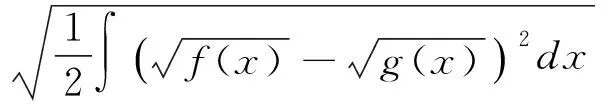
对于两个离散概率分布P=(p1,p2,…,pn)和

Q=(q1,q2,…,qn)， 它们的Hellinger距离定义为

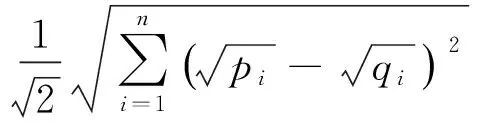
Hellinger距离具有如下性质：

(1) 0≤H(P,Q)≤1;

(2)H(P,Q)=H(Q,P);

(3)H(P,Q)=0当且仅当P=Q.

两个分布之间的Hellinger距离是非负和对称的.

2 判断矩阵排序方法

由Hellinger距离的性质可知， Hellinger距离可以作为两个离散分布相似程度的一个度量， 本节就以Hellinger距离作为优化问题的目标函数， 提出一种判断矩阵的排序方法.

设W=(w1,w2,…,wn)为判断矩阵A的排序向量， 由于W是归一化的， 因而可以视为一个离散分布.

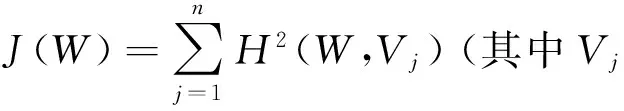
判断矩阵A的排序向量W为满足下面最优化模型的解.

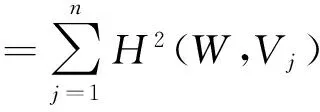
定理1 在上面的最优化模型中， 函数J(W)在Δn中可以确定W的一组最优解W=(w1,w2,…,wn),且W可以表示为下式

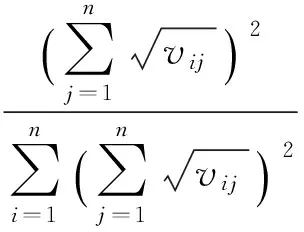
(1)

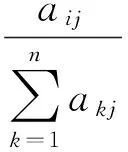
证明 用拉格朗日乘数法将条件极值转化为无条件极值. 构造拉格朗日函数

令

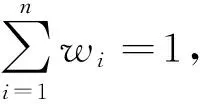
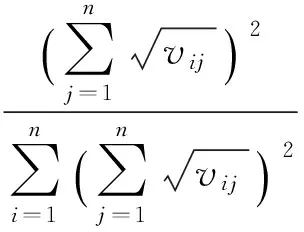
从(1)式可以看出， 基于Hellinger距离排序方法得到的排序向量实际上可以这样得到： 首先将判断矩阵A按列归一化， 对每一行的元素取根号， 然后将每一行求和， 再平方， 得到一个列向量， 最后将该向量归一化得到的向量就是排序向量.

3 排序方法的性质

一种排序方法， 可以看作由全体n阶正互反矩阵构成的集合Pn到全体排序向量构成的集合Δn的一个映射， 记作W=T(A)， 称W是判断矩阵A确定的排序向量.

定义2[8]一个排序方法称为强条件下保序的， 如果akj≥alj(∀j),能得到排序权值wk≥wl， 且当前者所有等式严格成立时， 有wk=wl.

定理2 基于Hellinger距离的排序方法是强条件下保序的.

证明 设W=(w1,w2,…,wn)是A=(aij)的基于Hellinger距离排序方法得到的排序向量， 则有

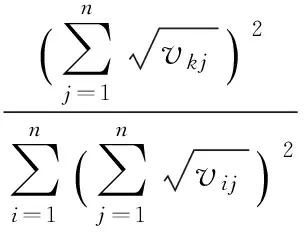
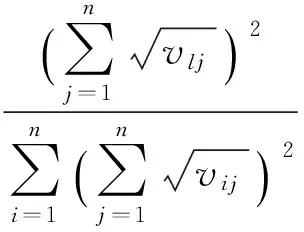
若akj≥alj(∀j)， 由wk，wl的表达式易见wk≥wl；若akj=alj时，wk=wl.因此， 基于Hellinger距离排序方法是强条件下保序的.

定义3[9]设T(·)是一种排序方法，A是任一个给定的判断矩阵，W=T(A).如果对于任一个置换矩阵P， 均有PW=T(PAPT)， 则称这种排序方法是置换不变的.

定理3 基于Hellinger距离排序方法具有置换不变性.

证明 设P是置换矩阵，B=(bij)=PAPT， 其中A为判断矩阵.设W=(w1,w2,…,wn)，X=(x1,x2,…,xn)分别是A,B的基于Hellinger距离排序向量， 经置换后A的第i行变为B的第k行，A的第i列变成了B的第k列. 于是

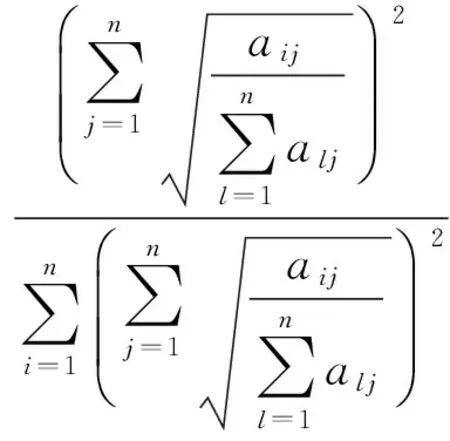
所以基于Hellinger距离的排序方法具有置换不变性.

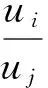
定义4[9]设T(·)是一种排序方法，W=T(A).如果A是一致的，W必是A的固有排序向量， 则称这种排序方法是相容的.

定理4 基于Hellinger距离排序方法具有相容性.

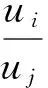
由于W=(w1,w2,…,wn)是A的基于Hellinger距离的排序向量， 故

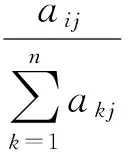
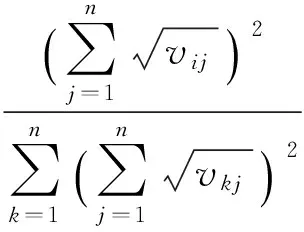
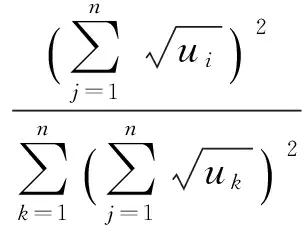
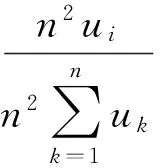
所以基于Hellinger距离的排序方法具有相容性.

4 实验验证

为了检验HDM排序方法的排序有效性, 我们取文献[10]中的判断矩阵A如下：

四种排序方法计算A的排序向量， 结果见表1.

对于矩阵A， 此时RI=1.12， 容易计算CR=0.0282<0.1， 一致性检验通过.

其中EM表示特征向量法；ANC表示和积法；HDM表示基于Hellinger距离排序方法；NGM表示方根法.

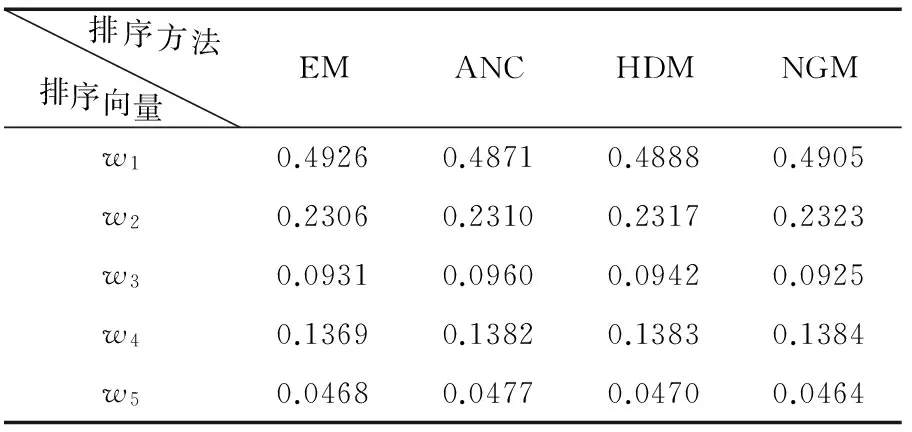
表1 矩阵A

从以上排序结果可以看出, 在判断矩阵满足一致性要求的情况下,基于Hellinger距离排序方法(HDM ) 取得了与特征向量排序方法完全一致的排序结果, 而且不同的方法所得排序权值很相近.由于HDM方法计算简单,是一种简易算法， 同另外两种简易算法ANC和NGM相比， 由HDM得到的结果总是介于由ANC和NGM得到的结果之间， 是这两种方法的折中.这些事实充分说明运用基于Hellinger距离排序方法对判断矩阵进行排序是可行且有效的.

5 结语

本文提出了一种基于Hellinger距离的判断矩阵排序方法,丰富和发展了层次分析法的排序理论.理论分析和数值结果均表明, 这种排序方法与特征向量排序方法的排序结果是完全一致的, 与和积法、 方根法所得排序权值很相近， 而且具有简洁、 可行、 且易于计算器或计算机上实施等优点.

[1] 袁杰,梁雪春.层次分析法中判断矩阵的一致性改进[J].统计与决策,2014(12):15-17.

[2] 吕跃进,程宏涛,覃菊莹.基于相对熵的互补判断矩阵排序方法[J].系统工程理论与实践,2011, 31(7):1328-1333.

[3] 雷功炎.关于将相对熵用于层次分析的简单注记[J].系统工程理论与实践,1995, 15(3):65-68.

[4] 章志敏,魏翠萍.层次分析若干理论与应用研究[J].曲阜师范大学学报,2013, 39(1):37-41.

[5] 王应明.判断矩阵排序方法综述[J].决策与决策支持系统,1995,5(3):104-114.

[6] 徐霄峰,上官金丽.层次分析法中一种新的保序方法[J].统计与决策,2011(6):35-37.

[7] 李伟湋,贾修一.基于Hellinger距离的特征选择算法[J].计算机应用,2010,30(6):1560-1532.

[8] 魏翠萍.关于层次分析法中和积法的最优化理论基础及性质[J].系统工程理论与实践,1999,19(9):113-115.

[9] 贾兰香,陈宝谦.层次分析决策方法排序问题的一般性质[J].南京大学学报,1991(2):19-28.

[10] 徐泽水.层次分析中判断矩阵排序的新方法——广义最小平方法[J].系统工程理论与实践,1998,18(9):38-43.

Judgment Matrix Sorting Based on Hellinger Distance

ZHAN Wan-rong, YU Hai

(College of Mathematics and Science, Luoyang Normal University, Luoyang 471934, China)

This paper provides a sorting method of judgment matrix, studies its isotonicity, consistency and compatibility. Lastly, Hellinger distance based sorting method is illustrated with examples and compared with eigenvector method, sum-product method and square root method. Theoretical analysis and calculation have proved the effectiveness of the title method.

analytic hierarchy process; judgment matrix; Hellinger distance; sorting method

N945.1

A

1009-4970(2017)11-0004-04

2016-11-17

国家自然科学基金资助项目(61272015)； 河南省高等学校重点科研项目(15A520087，16A520064)； 校青年科研基金项目(2013-QNJJ-002)

詹婉荣(1981—)，女，陕西西安人，硕士，讲师. 研究方向：模糊逻辑，粗糙集; 于海(1979—)，男，河南开封人，硕士，讲师. 研究方向：机器学习，粗糙集.

[责任编辑 胡廷锋]