不确定过程中增长性定理的一个证明
刘 乐, 贾耿华
(1.洛阳师范学院数学科学学院, 河南洛阳 471934; 2.洛阳理工学院数理部, 河南洛阳 471023 )
不确定过程中增长性定理的一个证明
刘 乐1, 贾耿华2
(1.洛阳师范学院数学科学学院, 河南洛阳 471934; 2.洛阳理工学院数理部, 河南洛阳 471023 )
不确定变量用来描述非确定性现象, 不确定过程就是一列随时间或空间变化的不确定变量.本文对不确定过程的增长性态进行研究, 并给出相关证明.
不确定变量; 不确定过程; 增长性态
刘宝碇教授[1]于2007创立了不确定理论, 用以研究人类的主观不确定性.作为处理主观判断或专家数据等不精确信息的新工具, 不确定性理论已引起了越来越多学者的关注, 已经成功应用于不确定规划[2]、 不确定金融[3-4]、 不确定微分方程[3-4]等等领域中.
1 基本概念
定理1.1[1]令(Γ,L)是可测集, L是Γ的σ-代数, 称Λ∈L为一个事件, 用M(Λ)来表示相信一个事件Λ会发生的信度. 如果M满足以下几条公理:
公理1.(正规性)M(Γ)=1;
公理2.(自对偶性)对任意事件Λ, 有
M(Λ)+M(Λc)=1;

定义1.1[1]不确定变量是从不确定空间(Γ, L, M)到实数集R的一个可测函数, 也就是说, 对任意R中的Borel集B, 集合{ξ∈B}={γ∈Γ|ξ(γ)∈B}是一个事件.
不确定积分是指不确定过程关于典范过程的积分.2009年, 刘宝碇教授[8]给出了一种重要的不确定过程典范过程的定义.
定义1.2[8]假设不确定过程Ct满足如下三个条件:
(1)C0=0, 几乎所有的轨道Lipschitz连续;
(2)Ct具有独立稳态增量;



定理1.2[1](MarkovInequality)设ξ为一个不确定变量, 任给t>0和p>0, 我们有

2 不确定过程增长性定理
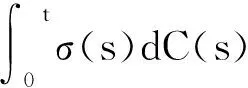
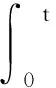
对于所有的t>0.






对所有的ε>0, 令
于是



又
等价于

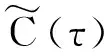

(3)由(1),(2)即可推得

再由t(τ)的定义得
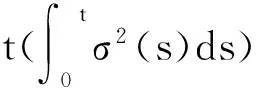

从而有
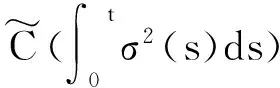

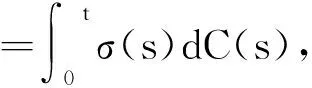
3 结论
本文对不确定过程的增长性态进行了研究, 给出了证明过程, 为以后的不确定微分系统性能分析奠定基础.
[1] Liu B. Uncertainty Theory[M]. 2nd ed. Berlin: Springer-Verlag, 2007.
[2] Zhu Y. Uncertain optimal control with application to a portfolio selection model[J]. Cyber-netics and Systems, 2010,41(7):535-547.
[3] Liu B. Uncertainty Theory: A branch of mathematics for modeling human uncertainty[M]. Springer-Verlag, Berlin, 2010.
[4] Peng J, Gao Y. A new option pricing model for stocks in uncertainty markets[J]. International Journal of Operations Research, 2011,8(2):18-26.
[5] Chen X., Liu B. Existence and uniqueness theorem for uncertain differential equations[J]. Fuzzy Optimization and Decision Making, 2010,9(1):69-81.
[6] Tao N, Zhu Y. Attractivity and stability analysis of uncertain di_erential systems[J]. InternationalJournal of Bifurcation and Chaos, 2015,25(2):1550022-1.
[7] Tao N, Zhu Y. Stability and attractivity in optimistic value for dynamical systems with uncertainty[J]. International Journal of General Systems, 2016,45(4):418-433.
[8] Liu B. Some research problems in uncertainty theory[J]. Journal of Uncertain Systems, 2009, 3(1):3-10.
The Proof of Growth Theorem of Uncertainty Process
LIU Le1, JIA Geng-hua2
(1. College of Mathematics and Science, Luoyang Normal University, Luoyang 471934, China; 2. Department of Mathematics and Science, Luoyang Institute of Science and Technology, Luoyang 471023, China)
Uncertain variable is used to represent quantities with uncertainty. An uncertain process is essentially a sequence of uncertain variables indexed by time. In this paper, we will study the growth state of the process, and give the corresponding proof.
uncertain variable; uncertain process; growth state; corresponding proof
O231
A
1009-4970(2017)11-0019-03
2017-03-29
洛阳师范学院教改项目(2016xjjg033)
刘乐(1979—), 女, 河南洛阳人, 硕士, 讲师. 研究方向: 运筹与控制论方面.
[责任编辑 胡廷锋]

