Ramanujan互反公式的一个注记
朱军明, 胡廷锋
(洛阳师范学院数学科学学院, 河南洛阳 471934)
Ramanujan互反公式的一个注记
朱军明, 胡廷锋
(洛阳师范学院数学科学学院, 河南洛阳 471934)
本文对Ramanujan互反公式的一个已有证明作了更正.
Ramanujan互反公式; 解析延拓; 基本超几何级数
1 假设
本文总是假设|q|<1,q阶乘使用如下通用的符号:


应用如下紧凑的记号:
(a,b, …,c;q)n=(a;q)n(b;q)n…(c;q)n; (a,b, …,c;q)∞=(a;q)∞(b;q)∞…(c;q)∞.
本文中, N 表示自然数集, 即N={0, 1, 2, ……}.
在Ramanujan“遗失”的笔记[1]中, 记载了如下的公式.
定理1 (Ramanujan) 对于a,b≠0且a,b≠-q-n(n∈ N), 我们有
(1)
其中
定理2 设函数f(z)与g(z)在区域D内解析,z0是D的内点. 如果在z0的任意空心邻域内都存在z∈D, 使得f(z)=g(z), 那么, 对任意z∈D, 都有f(z)=g(z).
把定理1中等式 (1)两端都看作b的函数, 观察容易发现, 在b=0时两端都不是b的解析函数, 因此, 定理2的条件并不满足, 即不满足定理2中要求f(z)与g(z)在b=0某邻域解析的条件, 因而文献 [3] 中的证明是有缺陷的. 我们很容易举出这样的反例.

本文借鉴了文献[3] 的思想, 但是克服了其证明中的错误.
2 定理1的证明
在以下的证明中, 我们将会用到Euler的q-指数函数[5]:
(2)
下面的Heine第二变换公式[5]也会被用到.
媳妇一跟我吵架,就哭着跑出去逛街购物,以发泄心中的不满。今天媳妇哭着对我说:“这日子没法过了,你已经一个星期没跟我吵架了。”
(3)
定理1的证明.我们先证明等式

(4)
此式即为
(5)
把 (5) 式两端都看作b的函数, 则它们都在b=0的邻域
内解析.在 (3) 中, 令α=q1-m,β=q,γ=aqm且δ→0, 我们得到
于是, 我们有

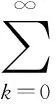



另一方面,


所以
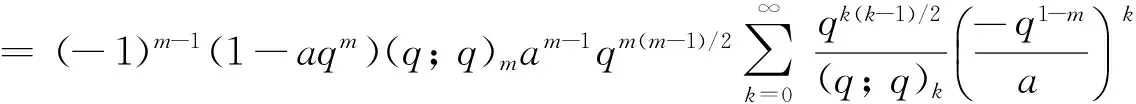
=(-1)m-1(1-aqm)(q;q)mam-1qm(m-1)/2(q1-m/a;q)∞


[1] Ramanujan S. The Lost Notebook and Other Unpublished Papers[M]. Narosa, New Delhi, 1988.
[2] Andrews G. Ramanujan’s “Lost” Notebook. I. Partialθ-functions[J]. Adv Math, 1981,41: 137-172.
[3] Adiga C, Anitha N. On a reciprocity theorem of Ramanujan[J]. Tamsui Oxf. J Math, 2006, 22: 5-15.
[4] Ismail M E H, A simple proof of Ramanujan’s1ψ1sum. Proc[J]. Amer Math Soc, 1977,63: 185-186.
[5] Gasper G, Rahman M. Basic Hypergeometric Series[M]. 2 ed. Cambridge: Cambridge University Press, 2004.
A Note on a Proof of Ramanujan’s Reciprocal Theorem
ZHU Jun-ming, HU Ting-feng
(College of Mathematics and Science, Luoyang Normal University, Luoyang 471934, China)
We revised a previous proof of Ramanujan’s reciprocal theorem by Adiga and Anitha.
Ramanujan’s reciprocal theorem; analytic continuation; basic hypergeometric series
O174.5
A
1009-4970(2017)11-0001-03
2017-07-31
国家自然科学基金资助项目(11371184)
朱军明(1973—), 男, 湖北应城人, 博士, 副教授. 研究方向: q-级数和theta函数.
[责任编辑 胡廷锋]

