三维喷动床内异径干湿颗粒混合特性数值模拟

李斌，于洋，马梦祥，张磊，陈翠玲

（华北电力大学能源动力与机械工程学院，河北 保定 071003）

三维喷动床内异径干湿颗粒混合特性数值模拟

李斌，于洋，马梦祥，张磊，陈翠玲

（华北电力大学能源动力与机械工程学院，河北 保定 071003）

基于计算流体力学-离散单元法，建立了三维喷动床内气固两相流数学模型，采用Fortran语言编制了并行数值模拟程序。对三维喷动床内两种不同直径的干颗粒及湿颗粒的混合特性进行了数值模拟，并从颗粒角度分析了双组分颗粒的运动机制。利用Lacey混合指数对床内整体以及特定区域的混合程度进行了定量分析，并研究了液桥体积、颗粒密度比以及表观气速对异径颗粒混合的影响。结果表明：在单孔射流喷动床内，干湿两种颗粒流动方式相似，湿颗粒无明显的聚团现象；液桥力对小直径的颗粒影响较大，使不同直径湿颗粒速度差减小；环隙区内颗粒的混合是影响整床颗粒混合的关键因素；液桥体积对颗粒混合的影响较大，对颗粒密度比以及表观气速的影响有限。

湿颗粒；两相流；混合；离散单元法；数值模拟

引 言

气固喷动床由于其优良的传热传质效果，广泛地应用于高效燃烧、制药涂层、颗粒造粒等工业生产中。目前对于喷动床内稠密气固两相流动中强烈的多尺度非线性的相间作用机理尚未完全了解，制约了喷动床等以气固流动特性为基础的设备的进一步发展。因此，对稠密气固流动的流动特性进行研究具有较大的实际意义。

许多学者通过实验手段对喷动床内气固流动特性进行了大量的基础研究[1-3]。但是由于实验条件以及测量方法的限制，仅有部分信息得以较为精确地测量及储存，颗粒受力、混合质量以及平均碰撞频率等颗粒层次的信息难以获得。而数值模拟作为弥补实验不足的手段，随着计算机能力和新数值模型的快速发展逐步成为研究气固两相流复杂行为的重要工具。目前，主要有两种主流的模拟稠密气固流动的方法：基于欧拉-欧拉框架的双流体模型[4](TFM)以及基于欧拉-拉格朗日框架下的离散单元法（DEM）。其中，离散单元法具有获取颗粒信息丰富、物理模型简单以及精确度较高的优点，得到了越来越广泛的应用[5-8]。

目前，已有学者对喷动床气固流动特性进行了大量研究[9-11]。其中对于喷动床内非均一颗粒的混合与分离特性是研究热点之一。Zhang等[12-14]对喷动床内不同直径以及密度的颗粒流动行为做了大量的实验，从实验角度详细地分析了气体喷动速度对床内颗粒流动的影响，并探讨了操作参数对混合速率的影响。Karimi等[15]对含有双组分颗粒的喷动床内不同喷动速度、初始颗粒堆积高度的影响进行了研究，并对最终的分离状态进行了预测。任冰等[16-17]对相同直径、不同密度以及相同密度、不同直径的颗粒在锥底喷动床内的混合过程进行了研究，得到了粒径比对流动结果的影响主要体现在喷泉区等有价值的结论。

而当喷动床用于干燥、食品加工等领域时，颗粒的表面将带有一定的液体。颗粒间的液桥力将会对颗粒的运动机制产生影响。徐慧斌等[18-19]对锥底喷动床内湿颗粒的流动特性进行了研究，讨论了液体含量与颗粒性质等对床内湿颗粒聚团的影响规律，并提出了湿颗粒条件下颗粒直径、初始床高以及喷口直径与最小流化速度的关系式。Nagahashi等[20]研究了半圆形喷动床内加入少量液体的影响，结果表明液体的注入会降低最小流化速度，增强流动过程。Sutkar等[21-22]提出了一种新型的非接触性测量技术，用于研究包含液体喷入的喷动床的流体动力学和传热性能，并进行了相应的数值模拟研究。Buijtenen等[23]通过考虑由于颗粒与液滴的相互作用对恢复系数的影响，进而研究了含水环境对床内动力学的影响。因为Sutkar等与Buijtenen等的研究对象为包含液体喷入的喷动床，因此其侧重于考虑颗粒与液滴的碰撞以及对颗粒的质量、恢复系数等因素的影响，而忽略液膜间液桥力的作用。而Zhu等[24]采用离散单元法，假设颗粒已携带均匀的液膜，着重考虑液膜间液桥力的作用，分析了不同液膜体积对喷动床内湿颗粒流动特性的影响，并对其混合行为进行了模拟研究。He等[25]采用类似的方法，对平底喷动床进行了模拟，并讨论了不同曳力模型的影响。但目前研究对象主要为均一颗粒，对喷动床内非均一湿颗粒的流动研究不足。

本文将计算流体力学以及离散单元法相结合（CFD-DEM），建立了三维平底矩形截面喷动床内稠密气固流动的四相耦合数学模型，采用 Fortran语言编制并行模拟程序，并进行了实验验证。对床内双组分的干、湿颗粒的流动过程进行模拟，以研究颗粒的混合特性以及影响因素。采用Lacey混合指数对喷动床内颗粒的混合程度进行定量分析，以揭示干、湿环境下颗粒的混合过程及机理。

1 数学模型

1.1 颗粒运动控制方程

颗粒主要受到周围气体的曳力、颗粒自身重力、颗粒之间以及颗粒壁面之间的碰撞力、液桥力的影响。颗粒相的运动过程可分解为平动和转动，根据牛顿第二定律，其平动方程为

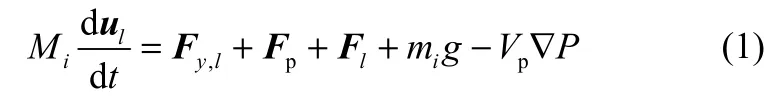
式中，Fy,l为流体对颗粒的曳力；Fl为颗粒间的液桥力；Fp为颗粒间的碰撞力，本文选择软球模型对其进行模拟，具体求解过程见文献[26]；Vp∇P为压力梯度力，考虑到其较重力以及碰撞力等力较小，本文模拟时忽略其影响。

转动方程

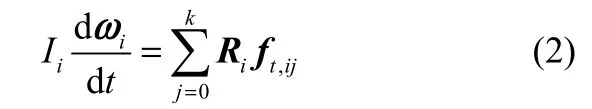
式中，ωi为颗粒旋转角速度；为球形颗粒转动惯量；k为与颗粒i发生碰撞的颗粒个数；Ri为颗粒质心到接触点的矢量；ft,ij为颗粒碰撞产生的切向力。

液桥力包括动态液桥力和静态液桥力两部分，两者的比值可以通过式（3）计算得到

式中，γ为填隙液体的表面张力，μl为填隙液体的黏性系数。在本文模拟的条件下，干颗粒的最大相对速度Δvp约为 2.2 m·s-1。计算可以得到动态液桥力与静态液桥力的比值约为0.03。因此为了简化计算，本文忽略动态液桥力的影响。为了模拟不同粒径间颗粒的液桥力，本文选取文献[27]中提出的液桥力模型

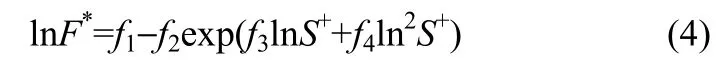
式中，液桥颈部的平均曲率半径R和其他量纲1参数定义为

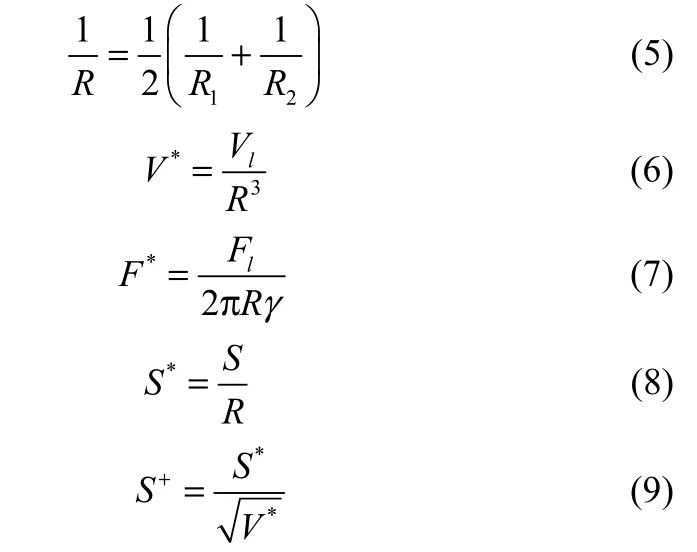
式中，R1,R2为液桥连接的两个颗粒的半径；Vl为液桥体积；V*为量纲1液桥体积；S为颗粒间距离。f1～f4的求解过程见文献[27]。

1.2 气相运动控制方程

气相运动控制方程考虑了气相与颗粒相间的相互作用力，并且采用k-ε两方程湍流模型建立了气固两相耦合的N-S方程组，最后采用SIMPLER算法进行求解。k-ε方程相关参数及具体求解过程见文献[26]。

1.3 气固两相之间的耦合作用

颗粒与气相的耦合主要由曳力来体现，本文选取经典的 Gidaspow曳力模型[28]，气体对颗粒的曳力如下。

当εg＞0.8时，利用Wen ＆ Yu方程得

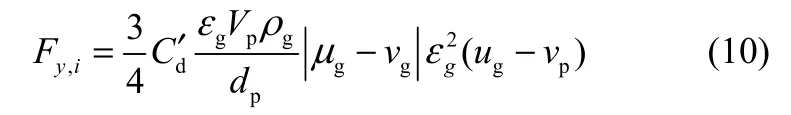
当εg≤0.8时，采用Ergun等式得

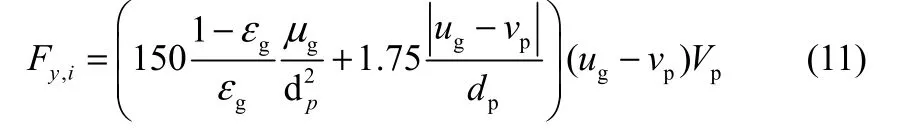
式中，μg为气体速度；vp为颗粒速度；ρg为气体密度；Vp为颗粒体积；dp为颗粒直径；C′d为有效曳力系数。

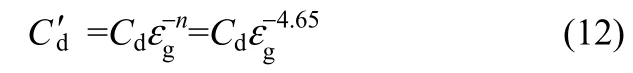
式中，n为空隙率修正因子，一般n的取值为-4.65；Cd为单颗粒的曳力系数。

当Rep≤1000时

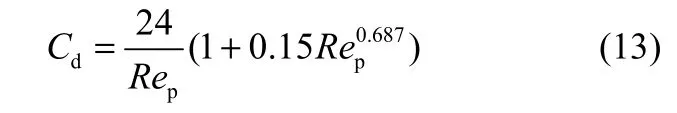
当Rep＞1000 时

颗粒Reynolds数的计算公式为

颗粒对气体的反作用力计算公式为

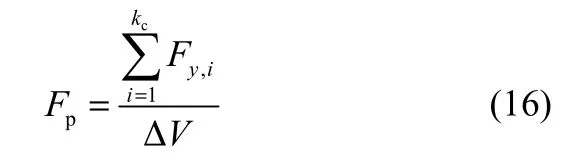
式中，Fy,i为气体对i颗粒的作用力。

2 模拟对象及参数

本文模拟对象为三维矩形截面喷动床，床体宽度×厚度×高度尺寸为150 mm×20 mm×900 mm。如图1所示空气入口布置在床底中心处，进气口尺寸为10 mm×20 mm。

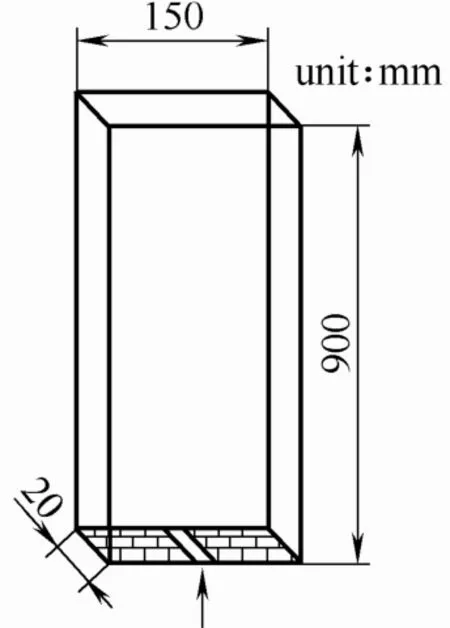
图1 模拟对象尺寸Fig.1 Geometry description of simulation object

气相在壁面处采用无滑移的边界条件，在出口处进行局部单向化处理，颗粒相则采用滑移边界条件。颗粒密度比k为大颗粒密度与小颗粒密度的比值。本文已进行网格无关性验证，模拟所用的具体参数见表1。

本文所模拟过程为二元颗粒在喷动床内混合过程，因此需要获得颗粒完全分离的初始状态。颗粒的初始位置由颗粒自由堆积获得。其具体过程为：颗粒位置在计算区域内无重叠随机生成，颗粒仅在重力作用下自由下落，经过一段时间后，颗粒速度趋近于零，即获得了颗粒的初始位置。计算得到的初始位置如图2所示。

表1 数值模拟参数Table 1 Parameters in numerical simulation

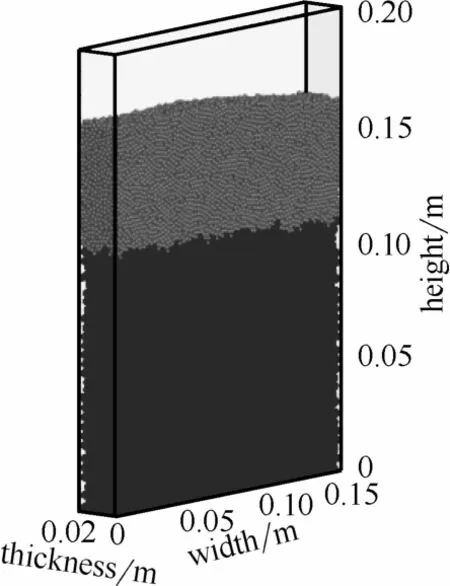
图2 颗粒初始位置Fig.2 Initial position of particles

3 结果分析及讨论

3.1 算例验证

为了验证程序的正确性，本文首先模拟了表观气速为2.33 m·s-1时，12000个4 mm直径的球形颗粒的流动状态，并拍摄了相同条件下喷动床内颗粒流场的瞬时图片。图3为模拟结果和实验结果的对比。通过对比可知，模拟与实验结果在颗粒位置与运动趋势上均吻合较好。

图4为床高0.3 m处的实验与模拟的颗粒时均速度分布，从图中可知，模拟结果与实验结果有较高的吻合度。由此表明程序的可靠性与数值方法的正确性。

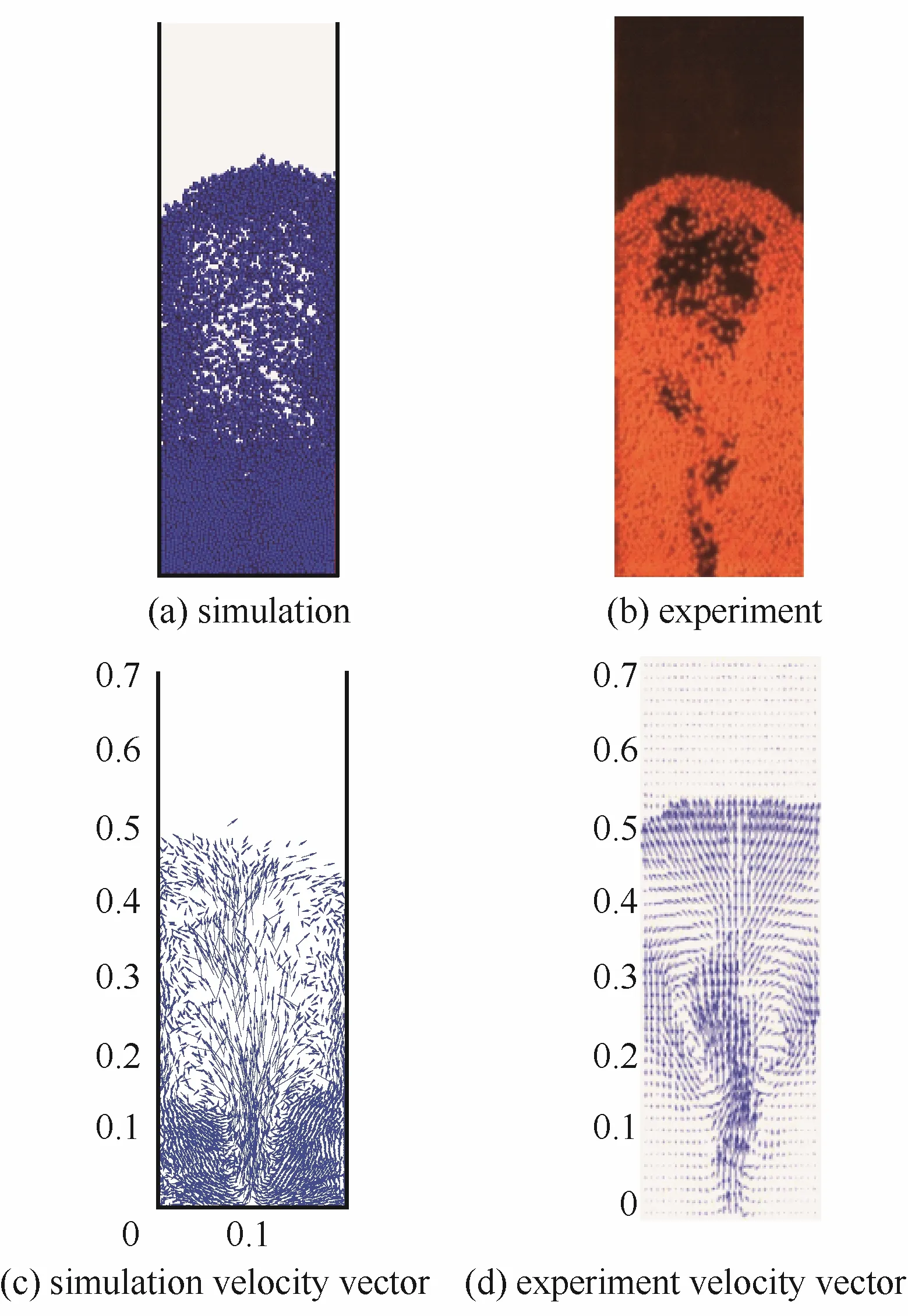
图3 模拟结果和实验的对比Fig.3 Comparison of simulated result with experimental result

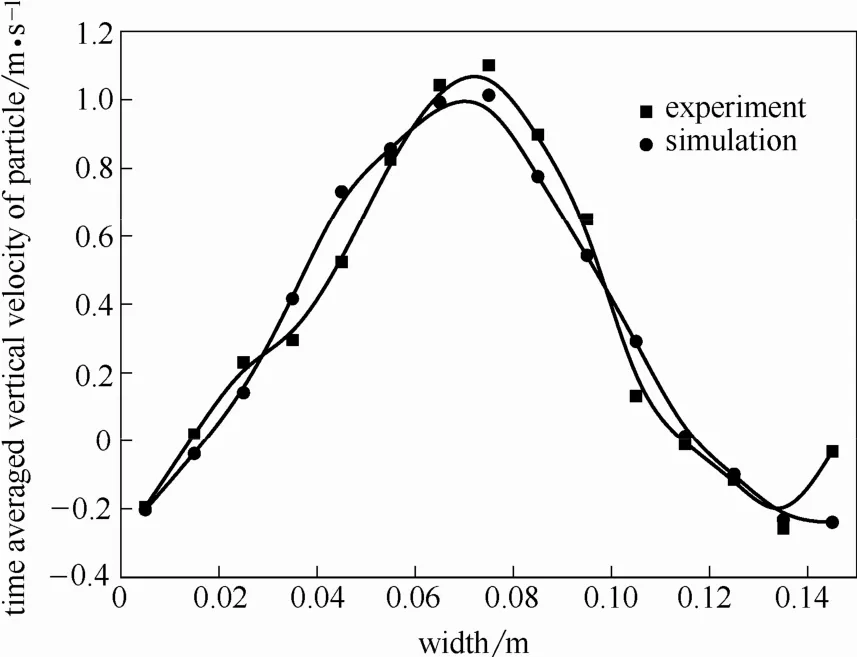
图4 床高为0.3 m处颗粒竖直时均速度分布Fig.4 Time averaged vertical velocity of particles where height was 0.3 m

3.2 喷动床内颗粒的混合序列图

图5为表观气速v=1.6 m·s-1，颗粒密度比k=1时，干、湿两种颗粒混合过程0～2 s的流化过程。图6为t=2 s局部颗粒速度矢量图。结合两图，从定性的角度看，两种颗粒在床内的流动相似。在喷口上方，颗粒受喷射气流夹带向上运动，由于气体的扩散作用，曳力不断减小，颗粒垂直方向呈先加速后减速的趋势，最终到达床体上部颗粒较为密集的区域。在此过程中颗粒由于碰撞力的作用逐步由喷口附近向靠近壁面的两侧扩散。在靠近壁面的区域由于曳力较小，颗粒运动由重力主导并开始下行回到床体下部密集区域。在该区域，颗粒由于气体的卷吸以及颗粒间碰撞的作用逐步由靠近壁面的区域斜下方向流动移动至喷口上方，进入下一循环。

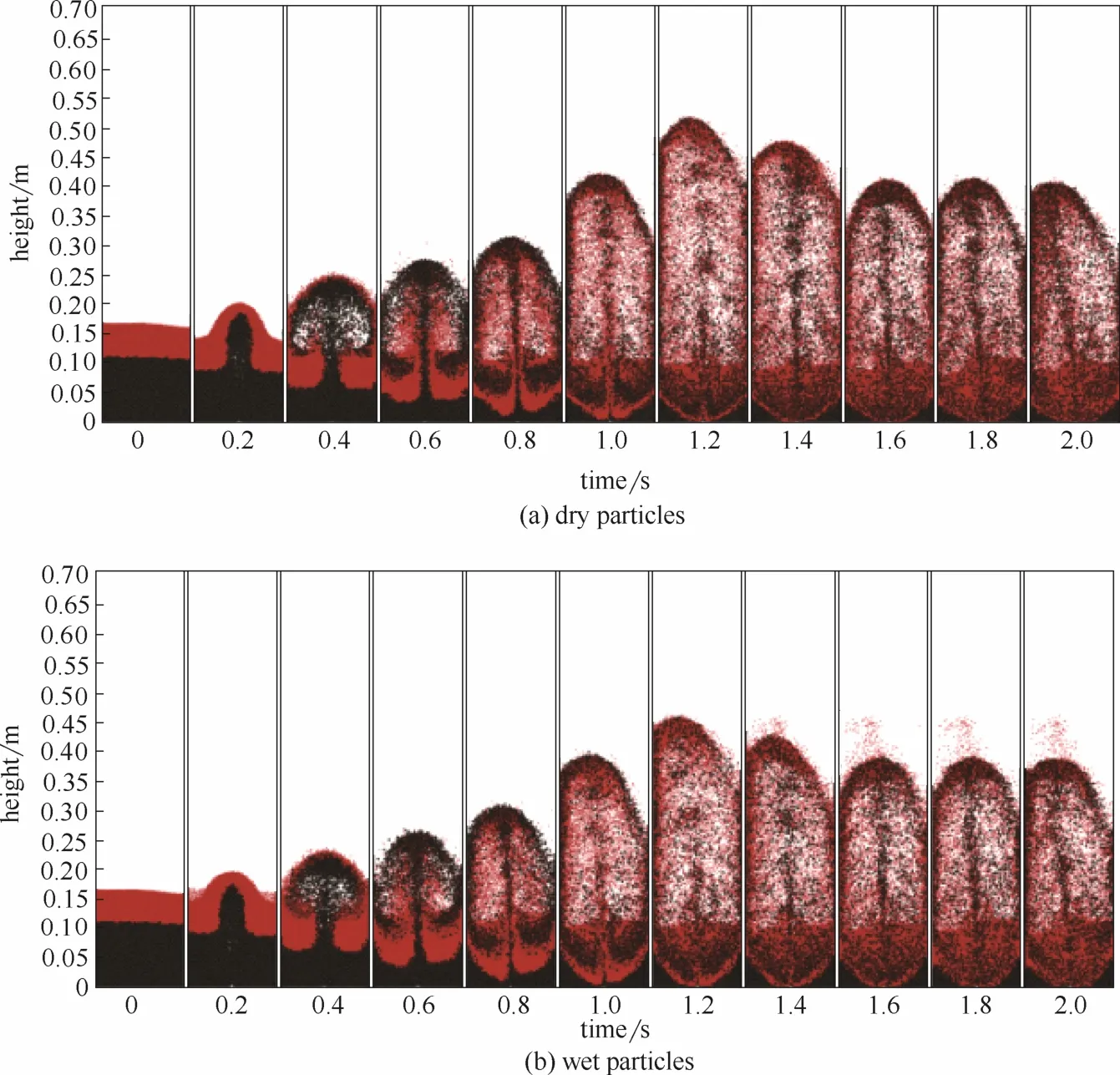
图5 干、湿颗粒混合序列Fig.5 Mixing sequence diagram of dry and wet particles

值得指出的是，在混合过程中床层膨胀高度存在明显的波动现象，而混合达到稳定状态后，膨胀高度较为稳定。这是由于模拟的初始状态为完全分离状态，下方颗粒均为大颗粒，颗粒对气体的反作用力较强，气体对颗粒的夹带效果有限。而后，随着喷动时间的增加，一方面小颗粒逐步进入喷动区，减弱了对气体的反作用；另一方面，床层顶部的大颗粒逐步回落，床层顶部密集区域的大颗粒减少，对下部颗粒的阻碍作用降低。两者共同作用使得床层高度增加。随着混合程度的不断加深，床层膨胀高度趋于稳定。从中可以看出，喷动床内大颗粒的流动形态决定了整体颗粒的流动形态。

干、湿两种颗粒的主要区别体现在喷泉区的上方以及死区。在图5(b)中，可以清晰地看出，在喷泉区上方，一些小的颗粒可以黏附在床体的前后壁面上，而干颗粒则无该现象。通过对比可以发现，在相同时刻，湿颗粒的死区较干颗粒的死区略大。这是因为在死区气体流动速度较低，曳力难以破坏颗粒初始的结构，液桥力使得颗粒间的受力更为紧密，最终使得湿颗粒死区的范围增大。

3.3 颗粒的受力分析

为了更好地阐释颗粒上述流动状态的成因，本文定量地分析了颗粒在床内不同位置的受力。图 7为不同区域颗粒所受作用力随时间的变化，其中喷动区采取床宽为0.07～0.08 m、床高为0～0.01 m的区域表征，喷泉区采取床宽为0.07～0.08 m、床高为0.36～0.37 m的区域表征，环隙区采取床宽为0～0.01 m、床高为0.15～0.16 m的区域表征。

从图7(a)中可以看出，由于靠近喷口，在喷动区颗粒受到曳力较大，在4×10-3N左右波动，与碰撞力数量级相同，两者远远大于液桥力。一方面由于喷口上方气体竖直方向速度远大于其他方向，因此气体曳力的竖直分量较大，而颗粒间的碰撞力方向由两个颗粒的位置决定，其竖直方向分量较小。另一方面，由于颗粒碰撞时间较短，而颗粒受曳力作用是持续的。因此，虽然在喷动区曳力略小于碰撞力，但是在竖直方向上颗粒运动由曳力主导，向上加速运动，而在水平方向上，颗粒主要由碰撞力主导，自床体中心向两侧移动。

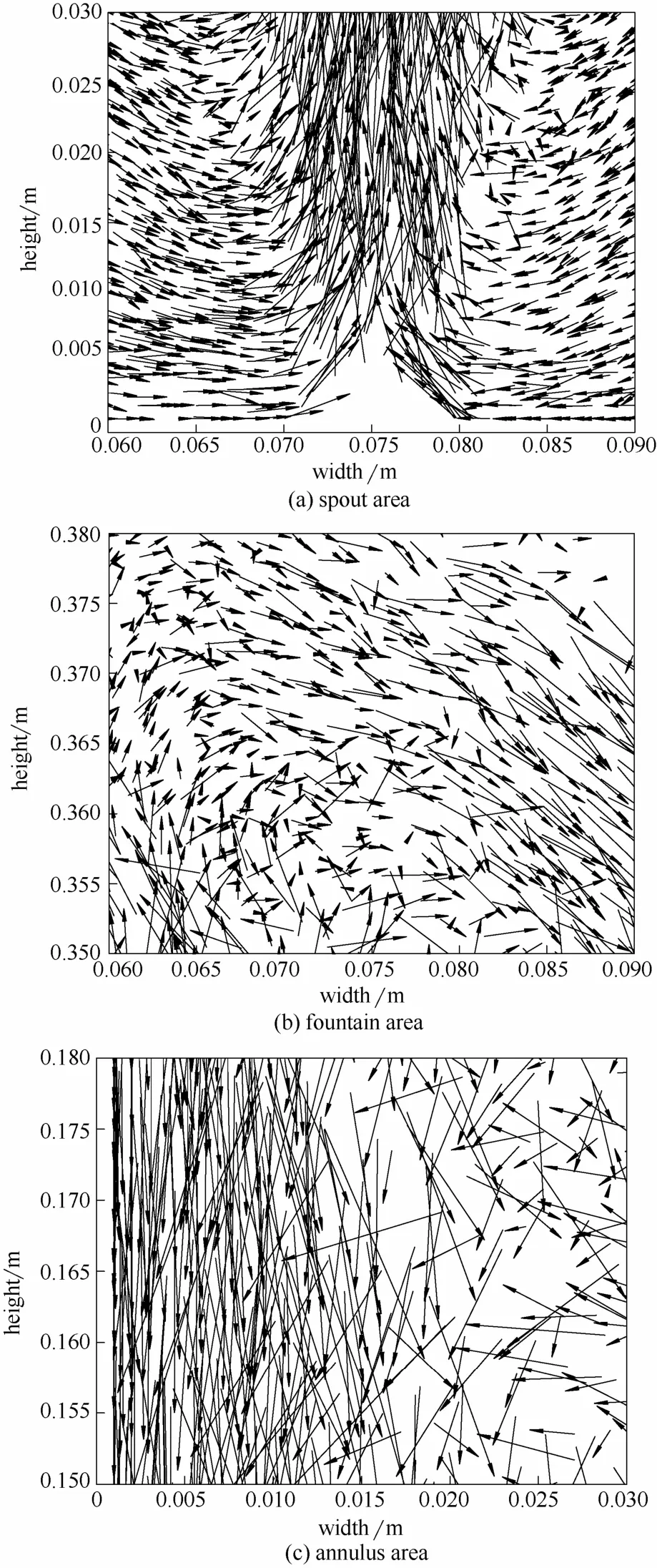
图6 颗粒速度矢量图Fig.6 Velocity vector diagram of particles

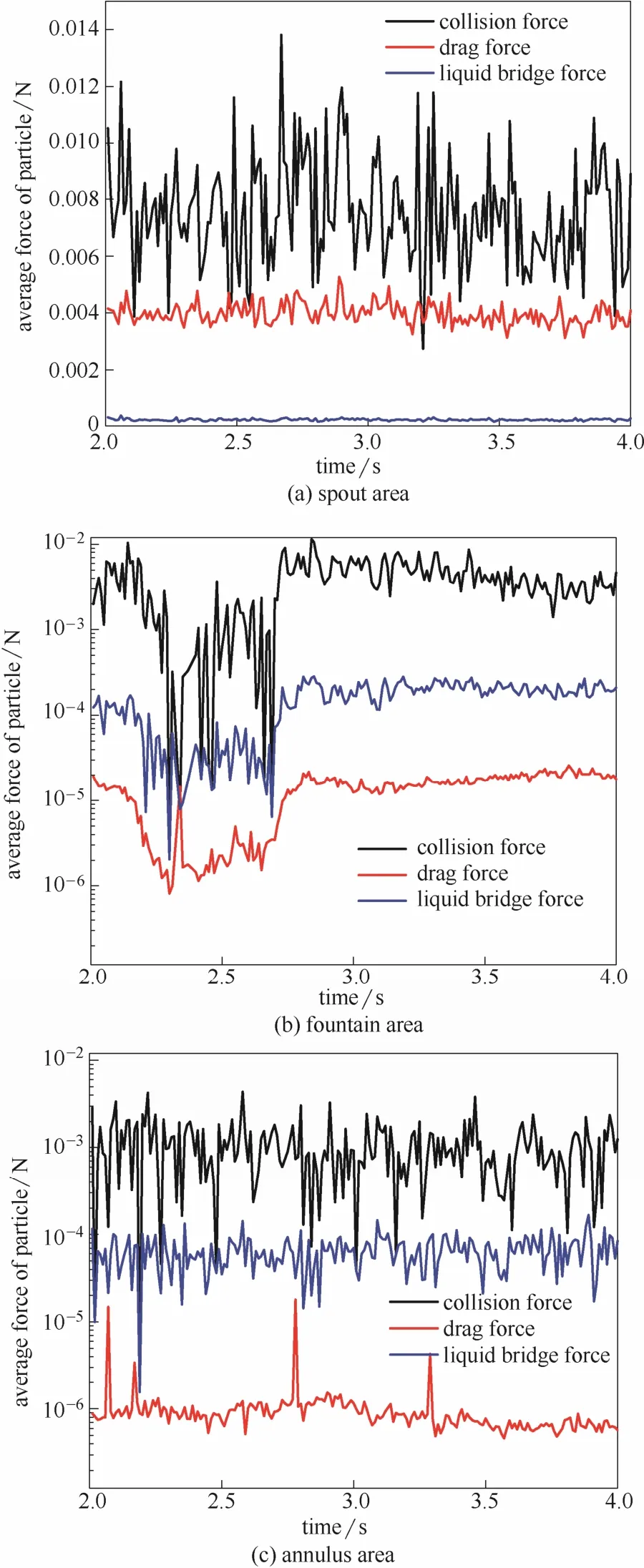
图7 颗粒受力随时间的变化Fig.7 Variation of force of particle with time

从图7(b)、(c)中可以看出，在喷泉与环隙区颗粒间的碰撞力在1×10-3N左右波动，较液桥力大一个数量级左右。结合图6(b)、(c)可以看出，喷泉区与环隙区不断受到来自喷动区的高速颗粒的冲击，与高速颗粒碰撞的颗粒受的冲量较大，因此具有较大的碰撞力，并且通过力链传递到其他颗粒，使得区域内整体所受碰撞力较大。而曳力由于气体速度较低，因此作用力较小。从图7（b）中可以看出，从2.2 s到2.6 s，颗粒所受碰撞力明显下降。此时，床层高度下降，统计区域位于喷泉区顶端，颗粒较为稀疏，使得颗粒的碰撞减少。

综合图7可知，在整床范围内碰撞力均大于液桥力，因此，颗粒受碰撞力的主导趋于分散。液桥力会延缓颗粒的分散过程，但无法形成稳定较大聚团。因此，干湿颗粒的流动状态较为相似。

3.4 颗粒的速度分布

为了更清晰地分析液桥力对颗粒流动的影响，本文分析了干湿颗粒速度的异同。图8为表观气速v=1.6 m·s-1，颗粒密度比k=1时，干、湿两种颗粒混合过程2～4 s颗粒不同床高处的时均速度分布。

从图8中可知，不同直径的颗粒速度分布均相似。在竖直方向上仅有远离壁面环隙区小颗粒速度略高于大颗粒。这是因为在底部床层与喷泉区颗粒相对稠密，颗粒间碰撞较为频繁，使得不同直径颗粒的速度趋于一致。而在远离壁面的环隙区，颗粒相对稀疏，颗粒的流动受到气体曳力的影响更为明显，且环隙区有足够的空间使颗粒分离，因此小颗粒的速度会大于大颗粒的速度。值得指出的是，由于初始位置的影响，颗粒流动略向左侧倾斜，喷泉区右侧颗粒同样较为稀疏。但是，由于喷泉区位置较高，颗粒处于受重力下行的初始阶段，颗粒速度很小，因此不同直径颗粒速度差异不明显。

与竖直方向运动相似，在水平方向上颗粒在稠密的底部床层与喷泉区部分速度相似；在颗粒相对稀疏的区域，小颗粒速度较为明显地大于大颗粒的速度。这可以从图8(b)、(d)中看出。由于颗粒流动的这一特性，使得颗粒达到稳定流动状态时，颗粒的混合程度较高。

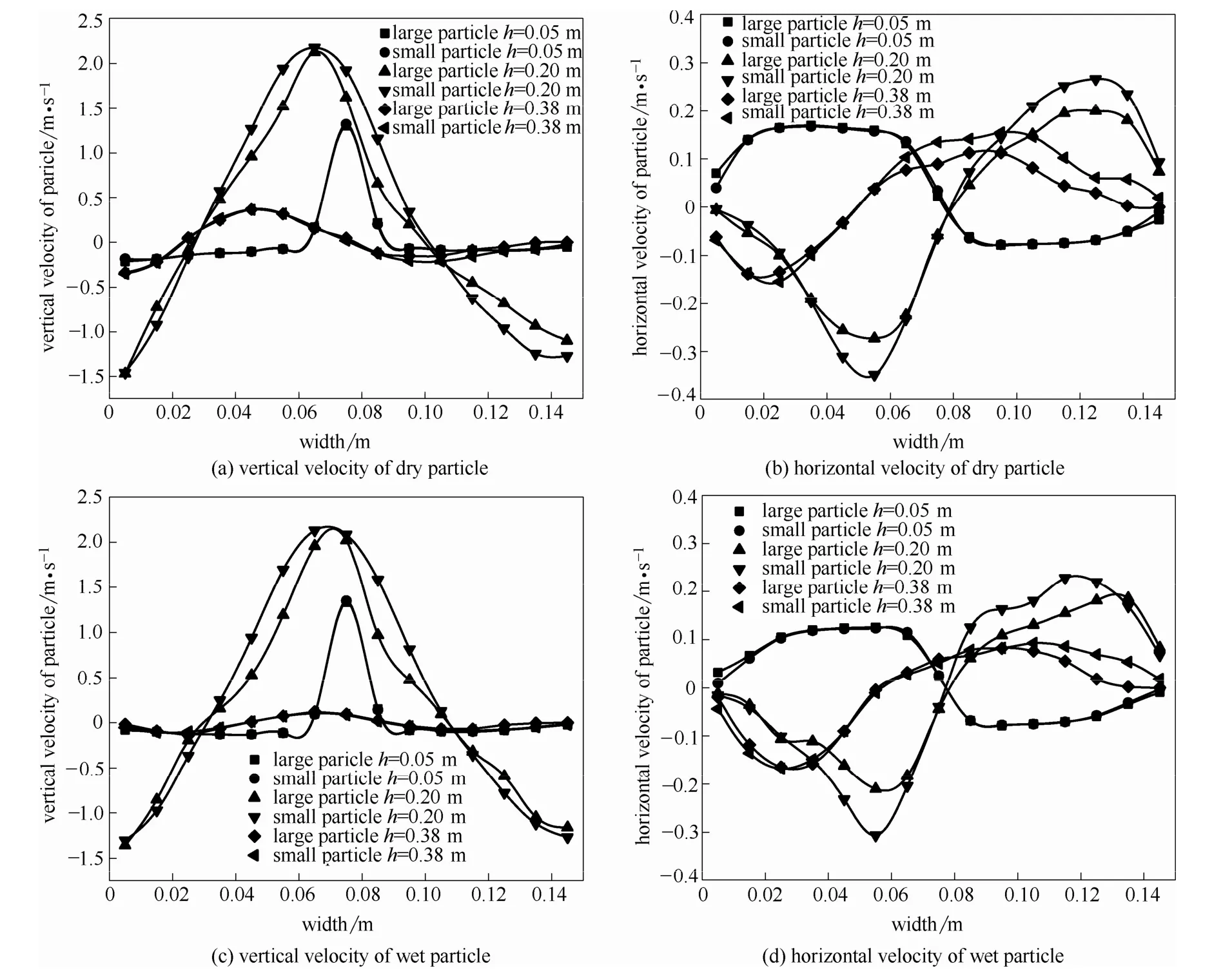
图8 颗粒分离和混合过程中不同高度时均速度分布Fig.8 Time averaged velocity of particles in different heights during separation and mixing process

而对比干、湿两种环境下颗粒的速度分布可以看出，两者的分布趋势相近，但速度大小不同。在竖直方向上，喷泉区的速度变化较为明显，干颗粒在床宽0.45 m左右存在高速运动区，湿颗粒速度分布则较为平滑，且速度远小于同位置的干颗粒。在底部床层以及靠近壁面的区域，湿颗粒速度均小于干颗粒的速度，尤其在床宽为 0～0.01 m、床高为0.045～0.055 m的区域内，大小颗粒的速度分别由-0.182 m·s-1及-0.211 m·s-1下降到-0.030 m·s-1及-0.079 m·s-1，液桥力对该区域内速度有显著的影响。造成上述现象的原因是这些区域颗粒较为稠密，颗粒间产生的液桥数目多，颗粒间液桥力较大，颗粒在加速过程中需要克服液桥力的影响，使得速度变小。

而在水平方向上，湿颗粒在整体床层内均较为明显地小于相应位置的干颗粒。这是由于气体的水平速度较低，因此曳力较小，颗粒主要受到碰撞力与液桥力的影响，液桥力对加速度的减弱效果更为明显。

同时，通过对比可以发现，湿颗粒不同直径的颗粒速度差比相同位置的干颗粒的速度差小。这是由于在大小两种颗粒间存在液桥时，液桥力大小相同，但是由于大颗粒质量较大，因液桥力引起的速度下降较小。最终使得不同直径颗粒的速度差降低。

3.5 混合与分离程度评价

为了定量分析喷动床内颗粒分离与混合特性，本文采用了Lacey随机混合指数[29]来描述颗粒的混合程度。取直径为4 mm的颗粒为示踪颗粒。为了量化系统中Lacey混合指数，床体被分为若干个取样单元，每个取样单元体积为10 mm×20 mm×10 mm，数据结果输出步长为0.1 s。统计标记颗粒在每个单元格的浓度，由此得出示踪颗粒在这些试样中含量的百分率的标准偏差。

Lacey混合指数

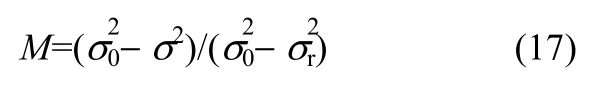
式中，σ为实际过程中示踪颗粒瞬时标准偏差；为完全分离时的示踪颗粒标准偏差；为完全混合时示踪颗粒标准偏差，l为取样单元中平均颗粒数目为全部取样单元内示踪颗粒平均浓度，ci为取样单元i内示踪颗粒浓度，N为取样单元数。

Lacey混合指数M反映了床内颗粒混合程度的量化，其值范围为0＜M＜1。M值越大，说明床内颗粒混合程度越高。反之则说明数据差别较大，混合程度相对较低。

图9给出了表观气速v=1.6 m·s-1时，颗粒整床及三区混合指数随时间的变化。从中可以看出，颗粒混合过程主要分为3个阶段：在0～1.2 s，整床颗粒混合指数可以快速地由0.015提升至0.701，这主要是因为大颗粒逐步完成了第1次循环的过程，随着时间的增加，不同直径的颗粒在喷泉区、环隙区与喷动区依次发生混合过程，由于颗粒初始状态为完全分离，因此该阶段颗粒的偏析作用较弱，颗粒混合较快。而后，在1.2～1.6 s，颗粒混合指数增速明显减缓，这是由于颗粒混合程度较高，偏析作用逐步增强。最终在1.6 s左右之后，达到混合与偏析作用的动态平衡，颗粒混合指数在0.85左右小幅波动。

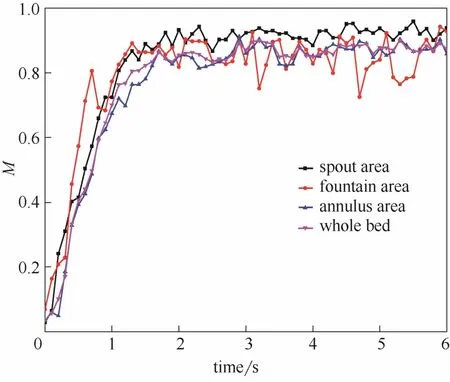
图9 整床及三区混合指数M随时间的变化Fig.9 Mixing index M in whole bed and different regions with time

对比整床混合指数与三区混合指数的曲线可以发现，整床颗粒混合达到稳定状态所需的时间与环隙区颗粒达到稳定状态的时间相近，相对于其他两个区域迟缓0.4 s左右，即环隙区内颗粒的混合是决定整床颗粒混合的关键因素，这与文献[30]中研究结果相同。

从混合指数的大小来看，喷动区的混合指数最高，在0.92左右波动，喷泉区与环隙区的混合指数相近，在0.88左右波动。这是因为环隙区与喷泉区的上方空间较大，颗粒较为稀疏，不同直径的颗粒运动存在较大的差异，加强了颗粒的偏析作用。从图中还可看出，喷泉区混合指数的波动最大，而喷动区与环隙区内颗粒混合指数相对稳定。这是由于喷床内存在颗粒的周期性喷动现象，使床层膨胀高度与颗粒上升的倾斜角度产生波动，对喷泉区的大小以及位置产生较大的影响。

3.6 颗粒混合特性的影响因素

图10展示了表观气速v=1.6 m·s-1，量纲1液桥体积不同时，颗粒混合指数随时间的变化。从图中可以看出，量纲1液桥体积对颗粒的混合速度影响较小。从图8中可以看出，在考虑液桥力后，喷动区内颗粒的竖直方向速度变化幅度较小，颗粒循环的时间相近，因此，对颗粒的混合速度影响有限。从图中还可看出，液桥体积对颗粒的混合程度有明显的影响。在0.6～1 s时，颗粒混合指数随量纲1液桥体积的增加而增大，结合图5可以看出，该时间段内小颗粒逐步进入喷动区，进而被喷动到床层上方。当量纲1液桥体积增加，液桥力随之增大，大颗粒对小颗粒的碰撞排挤作用减弱，更多的小颗粒伴随着大颗粒进入床层上部，促进了混合。而在1.6 s之后，颗粒流动趋于稳定，颗粒的混合指数随量纲1液桥体积的增大而减小。分析可知当液桥力增大时，黏附在壁面上的小颗粒数目随之增多；位于床体角落的死区由于液桥力的增大聚集得更为紧密，使得未参加流化的大颗粒数目增多，减弱了颗粒混合。

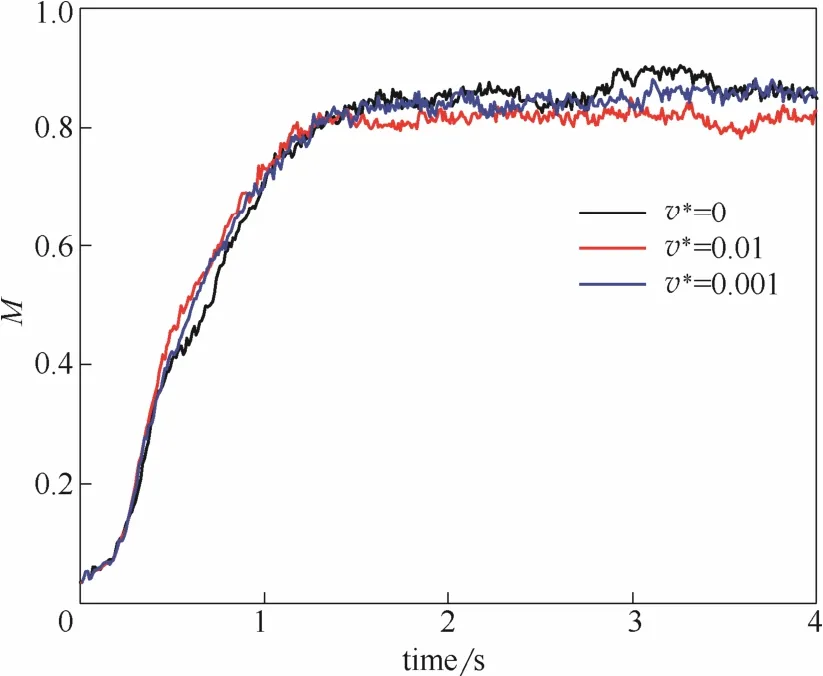
图10 不同量纲1液桥体积下混合指数M随时间的变化Fig.10 Variation of mixing index M with time at different dimensionless volumes of liquid bridge

图11(a)展示了表观气速v=1.6 m·s-1时，颗粒密度比不同时，颗粒混合指数随时间的变化。图11(b)展示了颗粒密度比k=1，不同表观气速下干颗粒混合指数随时间的变化。

从图11(a)中可知，颗粒密度比不同时，颗粒混合过程相似，在0.5～1.2 s，颗粒混合指数随密度的增大而略有增加；在达到稳定状态后混合指数的波动程度均随着密度比的增大而增大，但平均混合指数较为接近，均为0.783。在快速混合的初始阶段，即0～0.5 s，混合的主要形式为大颗粒受曳力影响进入上层小颗粒密集的区域，大颗粒的流动是影响混合的关键因素。在密度比不同时，大颗粒密度不变，因此在0～0.5 s，大颗粒流动相似，使得混合曲线几乎相同。在0.5～1.2 s，大颗粒在床层上部，小颗粒进入喷动区。小颗粒的质量随着密度比的增大而减小，因此更快地被气流喷动到较高的区域，促进了颗粒的混合。在颗粒混合达到稳定时，虽然小颗粒的速度与加速度会随着密度比的增大而增大，但一方面由于喷动区十分狭窄，小颗粒上行过程中易与慢速的大颗粒碰撞，使自身减速；另一方面由于喷泉区较为稠密，小颗粒难以穿过该区域达到更高的床层。因此，流动达到稳定状态时颗粒密度比不同时床内整体流动形式变化较小，混合指数较为接近。

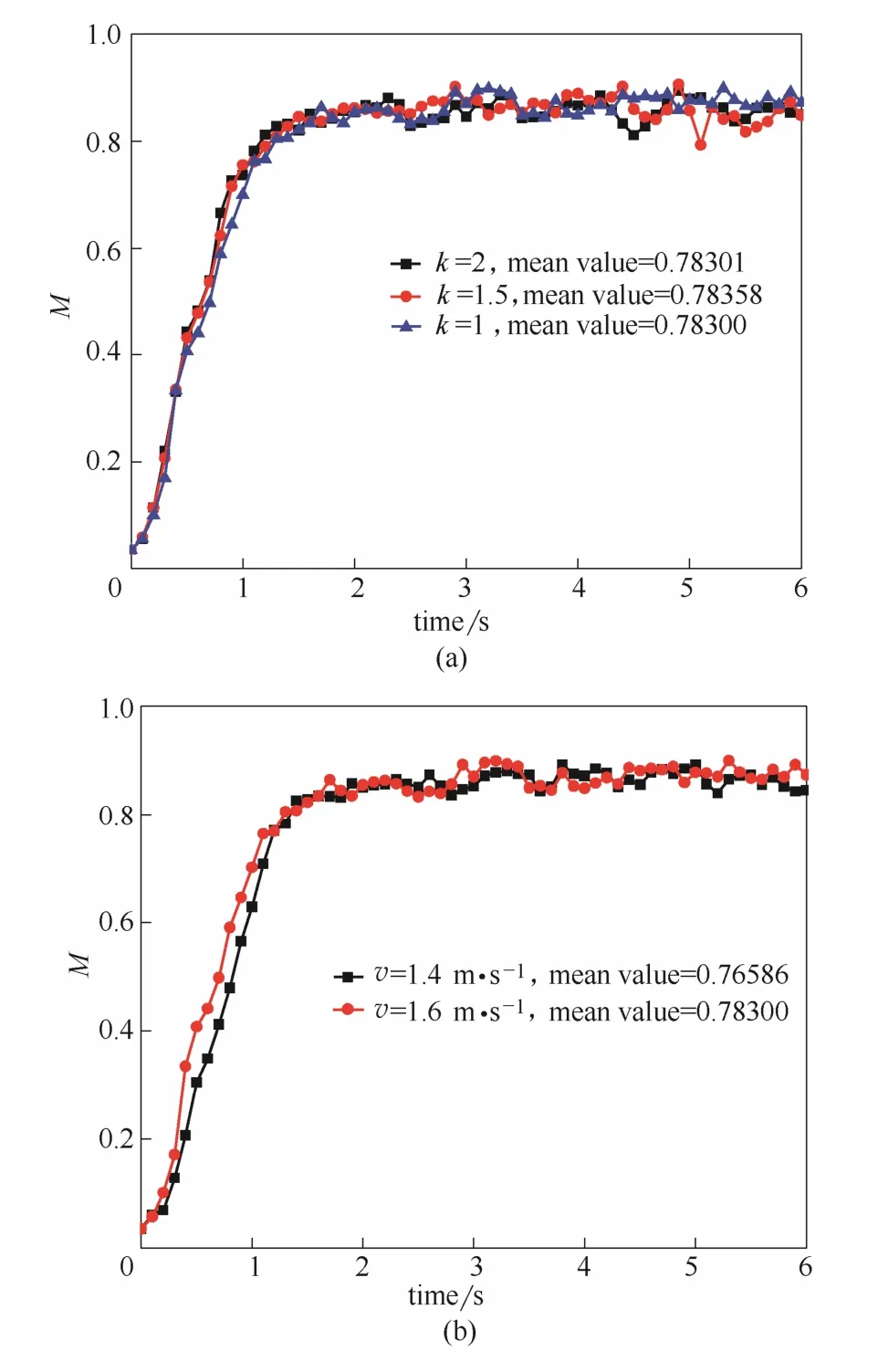
图11 不同密度比及表观气速下混合指数M随时间的变化Fig.11 Variation of mixing index M with time at different density ratios of particles and superficial gas velocities

从图11(b)中可知，在混合过程中，表观气速的影响较主要体现在初始的快速混合阶段。在0～1.2 s，较大表观气速的工况混合指数一直较高，在 0.4～0.9 s混合指数的差值在0.1左右波动。在1.2 s以后，不同表观气速下颗粒的混合指数相近，在0.85左右波动。这主要是因为在表观气速大的工况下，颗粒循环过程加快，使得在初始流化过程中，颗粒得以较早地进行混合，颗粒的混合指数增高。在稳定状态时，不同表观气速下的混合指数相近，因此，表观气速较大的工况颗粒混合指数的平均值略高。

4 结 论

本文基于CFD-DEM方法，运用Fortran语言编制了并行数值模拟程序，较好地模拟了实验室尺度不同直径干湿颗粒的流动过程，并进行了定量的分析，为工业尺度大规模的计算提供了基础。主要的结论如下。

（1）在单孔射流喷动床内，干湿两种颗粒流动方式相似。颗粒无法形成聚团的主要原因是由于颗粒间碰撞力远大于液桥力。

（2）液桥力减弱了碰撞力与曳力的作用。导致湿颗粒的速度低于干颗粒的速度，床体内死区范围大，对喷动床内整体流动产生一定的影响。

（3）颗粒在环隙区的混合对整床颗粒混合有较大的影响，整床颗粒的混合速度由环隙区内颗粒混合速度决定。由于环隙区内颗粒较为稀疏，不同直径颗粒流动差异较大，有利于不同直径的颗粒的偏析作用，该区域内颗粒混合程度与速度显著低于喷动区与喷泉区。

（4）液桥体积对颗粒的混合程度有较大的影响；表观气速对颗粒快速混合阶段影响较大；而密度比对颗粒的混合程度影响有限。三者对于颗粒混合达到稳定的时间无明显影响。

[1]SALIKOV V,HEINRICH S,ANTONYUK S,et al.Investigations on the spouting stability in a prismatic spouted bed and apparatus optimization[J].Advanced Powder Technology,2015,26(3)：718-733.

[2]LINK J M,DEEN N G,KUIPERS J A M,et al.PEPT and discrete particle simulation study of spout-fluid bed regimes[J].AIChE Journal,2010,54(5)：1189-1202.

[3]张勇,金保升,钟文琪.喷动气固流化床颗粒混合规律的实验研究[J].中国电机工程学报,2008,28(20)：8-14.ZHANG Y,JIN B S,ZHONG W Q.Experimental investigation on particle mixing in spout-fluid bed[J].Proceedings of the CSEE,2008,28(20)：8-14.

[4]VERMA V,DEEN N G,PADDING J T,et al.Two-fluid modeling of three-dimensional cylindrical gas-solid fluidized beds using the kinetic theory of granular flow[J].Chemical Engineering Science,2013,102(15)：227-245.

[5]YANG S,LUO K,FANG M,et al.Parallel CFD-DEM modeling of the hydrodynamics in a lab-scale double slot-rectangular spouted bed with a partition plate[J].Chemical Engineering Journal,2014,236(2)：158-170.

[6]YANG S,SUN Y,WANG J,et al.Influence of operating parameters and flow regime on solid dispersion behavior in a gas-solid spout-fluid bed[J].Chemical Engineering Science,2016,142：112-125.

[7]SALIKOV V,ANTONYUK S,HEINRICH S,et al.Characterization and CFD-DEM modelling of a prismatic spouted bed[J].Powder Technology,2014,270：622-636.

[8]彭丽,吴迎亚,李佳瑶,等.基于 DEM 模拟气固鼓泡床中颗粒碰撞参数对流场间歇性的影响[J].化工学报,2015,66(6)：2041-2048.PENG L,WU Y Y,LI J Y,et al.Effect of granular collision parameters on DEM simulation of flow field intermittency in gas-solids bubbling fluidized bed[J].CIESC Journal,2015,66(6)：2041-2048.

[9]张俊强,纪律,李斌,等.单孔射流流化床内颗粒混合特性的数值模拟[J].化工学报,2017,68(3)：879-888.ZHANG J Q,JI L,LI B,et al.Numerical simulation of particle mixing in single jet fluidized bed[J].CIESC Journal,2017,68(3)：879-888

[10]任立波,韩吉田.基于 CFD-DEM 耦合并行算法的锥形喷动床内离散颗粒数值模拟[J].东南大学学报(自然科学版),2014,44(5)：993-998.REN L B,HAN J T.Numerical simulation of discrete particles in conical-base spouted bed based on parallel coupled CFD-DEM mode[J].Journal of Southeast University (Natural Science Edition),2014,44(5)：993-998.

[11]GONIVA C,KLOSS C,DEEN N G,et al.Influence of rolling friction on single spout fluidized bed simulation[J].Particuology,2012,10(5)：582-591.

[12]ZHANG Y,ZHONG W Q,JIN B S,et al.mixing and segregation behavior in a spout-fluid bed：effect of the particle density[J].Industrial & Engineering Chemistry Research,2013,52(15)：5489-5497.

[13]ZHANG Y,ZHONG W Q,JIN B S,et al.Mixing and segregation behavior in a spout-fluid bed：effect of particle size[J].Industrial &Engineering Chemistry Research,2012,51(43)：14247-14257.

[14]ZHANG Y,ZHONG W Q,RUI X,et al.Evaluation of mixing and mixing rate in a multiple spouted bed by image processing technique[J].International Journal of Chemical Reactor Engineering,2016,15(1)：103-115.

[15]KARIMI H,MOLAEI D A.Prediction of equilibrium mixing state in binary particle spouted beds：effects of solids density and diameter differences,gas velocity,and bed aspect ratio[J].Advanced Powder Technology,2015,26(5)：1371-1382.

[16]REN B,SHAO Y,ZHONG W Q,et al.Investigation of mixing behaviors in a spouted bed with different density particles using discrete element method[J].Powder Technology,2012,222(5)：85-94.

[17]任冰,钟文琪,金保升,等.喷动床异径颗粒混合的离散元气固耦合模拟[J].工程热物理学报,2013,34(8)：1475-1478.REN B,ZHONG W Q,JIN B S,et al.DEM simulation of mixing behaviors of binary particles with different sizes in spouted beds[J].Journal of Engineering Thermophysics,2013,34(8)：1475-1478.

[18]XU H B,ZHONG W Q,YUAN Z L,et al.CFD-DEM study on cohesive particles in a spouted bed[J].Powder Technology,2017,314：377-386.

[19]徐惠斌,钟文琪,Yu Aibing.湿颗粒喷动床颗粒聚团特征的实验研究[J].工程热物理学报,2017,38(1)：124-128.XU H B,ZHONG W Q,YU A B,et al.Experimental study on the agglomerate characteristics of particles in the wet spouted bed[J].Journal of Engineering Thermophysics,2017,38(1)：124-128.

[20]NAGAHASHI Y,EPSTEIN N,GRACE J R,et al.Spouting enhancement by addition of small quantities of liquid to gas-spouted beds[J].Canadian Journal of Chemical Engineering,2010,84(5)：527-531.

[21]SUTKAR V S,DEEN N G,PATIL A V,et al.Experimental study of hydrodynamics and thermal behavior of a pseudo-2D spout-fluidized bed with liquid injection[J].AIChE Journal,2015,61(4)：1146-1159.

[22]SUTKAR V S,DEEN N G,PATIL A V,et al.CFD-DEM model for coupled heat and mass transfer in a spout fluidized bed with liquid injection[J].Chemical Engineering Journal,2016,288：185-197.

[23]BUIJTENEN M S,DEEN N G,HEINRICH S,et al.A discrete element study of wet particle-particle interaction during granulation in a spout fluidized bed[J].Canadian Journal of Chemical Engineering,2010,87(2)：308-317.

[24]ZHU R R,ZHU W B,XING L C,et al.DEM simulation on particle mixing in dry and wet particles spouted bed[J].Powder Technology,2011,210(1)：73-81.

[25]HE Y,PENG W,TANG T,et al.DEM numerical simulation of wet cohesive particles in a spout fluid bed[J].Advanced Powder Technology,2016,27(1)：93-104.

[26]李斌,纪律.流化床炉内颗粒混合的离散单元法数值模拟[J].中国电机工程学报,2012,32(20)：42-48.LI B,JI L.Numerical simulation of particle mixing in circulating fluidized bed with discrete element method[J].Proceedings of the CSEE,2012,32(20)：42-48.

[27]孙其诚,王光谦.颗粒物质力学导论[M].北京：科学出版社,2009.SUN Q C,WANG G Q.Introduction to the Granular Matter Mechanics [M].Beijing：Science Press,2009.

[28]LI T,ZHANG Y,HERNÁNDEZ-JIMÉNEZ F.Investigation of particle-wall interaction in a pseudo-2D fluidized bed using CFD-DEM simulations[J].Particuology,2016,25：10-22.

[29]LACEY P M C.Developments in the theory of particle mixing[J].Journal of Chemical Technology & Biotechnology,1954,4(5)：257-268.

[30]朱润孺,朱卫兵,邢力超,等.矩形喷动床混合特性的三维数值研究[J].中国电机工程学报,2010,30(17)：12-16.ZHU R R,ZHU W B,XING L C,et al.A three-dimensional numerical investigation on particle mixing characteristics in rectangular spouted beds[J].Proceedings of the CSEE,2010,30(17)：12-16.

date:2017-05-31.

YU Yang,15831516592@163.com

supported by the National Natural Science Foundation of China(11602085) and the Natural Science Foundation of Hebei Province(E2016502098).

Numerical simulation of mixing different sized wet and dry particles in three-dimensional spouted bed

LI Bin,YU Yang,MA Mengxiang,ZHANG Lei,CHEN Cuiling
(School of Energy Power and Mechanical Engineering,North China Electric Power University,Baoding071003,Hebei,China)

Based on framework combined discrete element method and computational fluid dynamics,a gas-solid flow model in three-dimensional spouted bed was established and Fortran numerical simulation program was further developed.The mixing characteristics of two different diameter-sized wet or dry particles in three-dimensional spouted bed were simulated and the mixing mechanism of binary particles in the spouted bed was analyzed.Lacey mixing index was introduced to quantitatively analyze degree of mixing in whole bed and specific regions of the bed.The influences on mixing different sized particles were studied by volume of liquid bridge,ratio of particle densities and superficial gas velocity.The results show that both wet and dry particles flow similarly in single jet spouted bed without obvious agglomeration of wet particles.Liquid bridge had a greater influence on small particles than large ones,which reduced difference of velocity between wet particles with different diameters.Particle mixing in circular groove was critical to mixing across whole bed.Liquid bridge volume had a more significant influence on particle mixing,compared to ratio of particle densities and superficial gas velocity.

wet particle; two-phase flow; mixing; discrete element method; numerical simulation

TQ 051.1

A

0438—1157（2017）12—4545—11

10.11949/j.issn.0438-1157.20170700

2017-05-31收到初稿，2017-07-28收到修改稿。

联系人：于洋。

李斌(1969—)，男，博士，副教授。

国家自然科学基金项目(11602085）；河北省自然科学基金项目(E2016502098)。