一种基于多无人机的中继节点布置问题建模与优化方法

吴高峰，高晓光，符小卫

西北工业大学 电子信息学院，西安 710072

一种基于多无人机的中继节点布置问题建模与优化方法

吴高峰，高晓光*，符小卫

西北工业大学 电子信息学院，西安 710072

针对战场环境下急需在无法通信的节点间构建有效通信链路的情形，使用多无人机作为中继节点，建立了中继节点布置(RNP)问题模型。模型以中继链路有效和无人机安全为约束，以中继布置点位置及相应的无人机为输出，不但考虑了使用的中继无人机数量，还考虑了构建中继链路花费的时间。考虑到该问题是难以求解的混合整数多目标优化问题，同时在紧急应用情形下，要求求解算法快速有效，建立了一种多项式时间中继节点布置算法(PTRPA)。仿真实验验证了所提模型确实能够在更短的时间内完成有效中继链路构建；通过Monte-Carlo方法对比和分析不同因素对PTRPA算法、随机抽样算法、遗传算法求解该问题的结果性能和时间性能的影响，验证了PTRPA算法不但能够给出接近最优的解，且快速有效，满足战场决策需求。

无人机；中继；无线通信；节点布置；多项式时间算法；多目标优化

现代作战具有高度信息化、网络化的特点，实现与保持作战节点间的信息交互十分重要。在信息交互的诸多实现方法中，无线通信是作战环境下最为重要的通信方式之一。然而，随着无线信号传输距离的增加，接收信号功率不断下降，并且易受到地形等因素的阻碍，导致节点与节点间无法通信[1]，解决该问题的一种有效方法是在合理的位置布置新的节点作为通信中继来转发节点间消息。因此，如何选择中继节点数量和位置成为其中的关键问题，即中继节点布置(Relay Node Placement, RNP)问题。

中继节点布置问题研究中，由于中继节点(Relay Node, RN)类型和应用背景不同，中继布置的目标也存在差异，现有的研究中主要包括：使用最少数量的中继节点实现网络的连通(Connectivity)或容错(Fault-Tolerance)[2-4]、尽可能地降低能耗(Energy Consumption)以最大化网络寿命[5-7](Lifetime)、提升网络的通信服务质量[8](Quality of Service, QoS)、平均覆盖率[9-10](Average Coverage)、容量[11-12](Capacity)和安全性[13](Safety)。

本文以布置多无人机作为中继在急需通信的两节点间构建通信链路为背景，研究RNP问题，这在一些作战情形下具有较大意义，如远处执行战场态势收集任务的节点与指控中心通信突发中断。此外，无人机作为空中移动平台，具有以下优点：① 相对于地面中继平台，部署周期短、灵活性高且通信质量好；② 相对于有人机平台，战场生存能力强、效费低；③ 相对于卫星中继平台，抗干扰能力强、延迟低[14-17]。因此，使用无人机作为中继具有重要应用价值。

从无人机研究角度看，无人机RNP问题也是无人机中继任务规划问题，考虑的因素包括使用的无人机数量[13]、中继质量[14,18]、连通性[19]、无人机安全性指标[13]。无论是RNP问题研究领域[2-13]，还是无人机中继任务规划研究领域[13-14,18-19]，尚未有研究考虑如何缩短构建中继链路花费的时间，而在急需构建中继链路的情形下，缩短构建中继链路花费的时间往往比追求更高的通信质量更有意义。因此，本文RNP建模与优化重点考虑的是在能够通信的前提下，如何通过确定中继布置点位置及对应的无人机来使使用的无人机数量尽可能少和构建中继链路花费的时间尽可能短。本文研究属于无人机中继任务规划决策层[20]。

基于无人机的RNP问题研究中，考虑的因素除通信距离约束、视线(Line of Sight, LoS)通信约束外，还包括节点安全约束。文献[13]考虑了环境中存在的地形因素对无人机的安全威胁，战场环境下往往还存在敌方防空覆盖区域，因此也要避免将中继无人机布置在这些区域，值得注意的是，无线信号往往可以穿越这些区域。

综上所述，针对以无人机作为RN在两节点间紧急构建中继链路情形，需要同时考虑到无人机数量最少和构建中继链路时间最短，且需要考虑通信距离、地形障碍和敌方防空威胁约束。该问题是一个混合整数多目标优化问题，且求解难度NP-hard[21]。求解此类问题的传统优化方法包括遍历求解空间以获得均衡解，以及将多目标函数转化为单目标函数。前者决策时间过长，不符合紧急情形下的实时决策要求，后者又带来加权、约束等新的复杂问题。另一类是以遗传算法、粒子群算法等为代表的智能优化算法[22]，但是该类算法仍然需要花费较长时间，同样难以满足要求。文献[23-24]针对多无人机多目标优化问题，给出了一种两阶段算法，通过排序和删减的方式得到无人机联盟成员，然而该类文献中各无人机目标位置点相同，而本文中各无人机的中继布置点不同，且相邻无人机间存通信距离约束，使得上述方法难以适用于本文的RNP问题。本文建立了一种满足多项式时间中继节点布置算法(Polynomial Time Relay Placement Algorithm,PTRPA)，该方法先通过广度优先搜索的方法求取最少中继无人机数量并缩小求解空间，再通过贪婪策略优化构建中继链路花费的时间。一旦无人机到达各自中继布置点并实现构建中继链路，需要继续控制中继无人机运动以保证中继效果，Dixon和Frew在文献[25]中对此做了一定程度的研究。

本文针对紧急情况下的中继无人机布置问题，建立了相应的优化模型，不但考虑了使用的中继无人机数量，而且考虑了构建中继链路花费的时间。针对该问题求解难度NP-hard，本文给出了一种多项式时间求解算法，并分析了算法的计算复杂度。本文的组织结构如下：第1节建立了基于多无人机的中继节点布置问题数学模型；第2节通过对问题空间进行离散处理，使得此问题由连续的混合整数规划问题变为可解的离散整数规划问题；第3节详述了本文提出的两阶段多项式时间中继节点布置算法PTRPA；第4节通过仿真检验了算法的可行性和有效性并研究了不同因素对算法性能的影响；第5节是对全文的总结。

1 基于多无人机的中继布置问题建模

为了研究问题的方便，假设所有的节点处于同样的海拔高度，战场区域为D⊂R2,待中继的目标节点为s和t,考虑到中继无人机多为中小型无人机，最大飞行高度有限，无人机以一定高度在该区域内执行中继任务，区域内可能存在敌方防空威胁和地形障碍威胁，并分别记其覆盖区域为Y={y1,y2,…,yb}和Z={z1,z2,…,za},有m架无人机U={u1,u2,…,um}可用作中继节点。

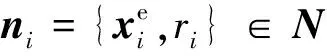
(1)

式中：

f1(N)=k

(2)

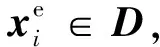
(3)

需要指出的是，s和t之间的RNP研究与s到t的航路规划研究存在本质区别：① 飞行航路需要考虑无人机飞行特性，航路曲线是平滑的，而中继链路是由多条直线段组成的折线；② 研究目的不同，前者是给出中继布置点位置和对应的无人机，后者是生成两点间的可飞航路。

接下来，中继节点布置过程中，还需要考虑到中继无人机的安全性、通信链路有效性以及一个无人机只能被布置到一个中继布置点，具体来说：

1) 中继无人机安全性约束：为了保证无人机安全，同时也是为了保证中继链路持续可靠工作，首先要求中继布置点避开地形障碍和敌方防空威胁覆盖区域，即

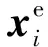
(4)

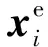
(5)

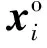
∀pi∩Z=∅i=1,2,…,k

(6)

∀pi∩Y=∅i=1,2,…,k

(7)

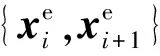
考虑到地形障碍容易阻隔无线信号传播，而敌方防空武器却难以阻隔无线信号传播，于是要求:

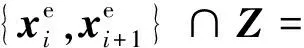
(8)

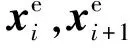
(9)

3) 中继无人机唯一性约束：中继节点布置中，任意无人机只能被布置在唯一的布置点，即

∀ri≠∀rji=1,2,…;k,j=1,2,…,k

(10)

本文基于多无人机的中继节点布置问题式(1)～式(10)是一个难以求解混合整数多目标优化问题，不仅是因为该问题中存在整数变量，还因为区域内可能存在多组可行的中继布置点、中继布置点与中继无人机组合方式不同带来不同的f2(N)、以及存在的地形障碍和敌方防空威胁覆盖区域可能会产生多极值。

本文接下来工作的目标是给出一种针对上述RNP问题的快速有效求解算法，以满足战场决策要求。考虑到该问题属于连续空间优化问题，为便于问题求解，首先对问题空间进行离散化处理。

2 空间离散化

为求解中继节点布置问题式(1)～式(10)，将中继节点布置范围限制在等间距的离散点D′⊂D,如图1所示，γ为布置点间距，浅色区域为地形障碍覆盖区域，深色区域为敌方防空威胁覆盖区域，黑色点为不可行布置点，白色点为可行布置点。令Z′=Z∩D′及Y′=Y∩D′,于是可以得到可行布置点位置集合X=D′-Z′∪Y′。

令矩阵C=[cij]|X|×|X|表示可行布置点间通信连接关系，|X|表示X中可行布置点数目，cij=1表示可行布置点xi∈X和可行布置点xj∈X之间存在视线路径且距离小于无人机最大通信距离dmax,即

(11)

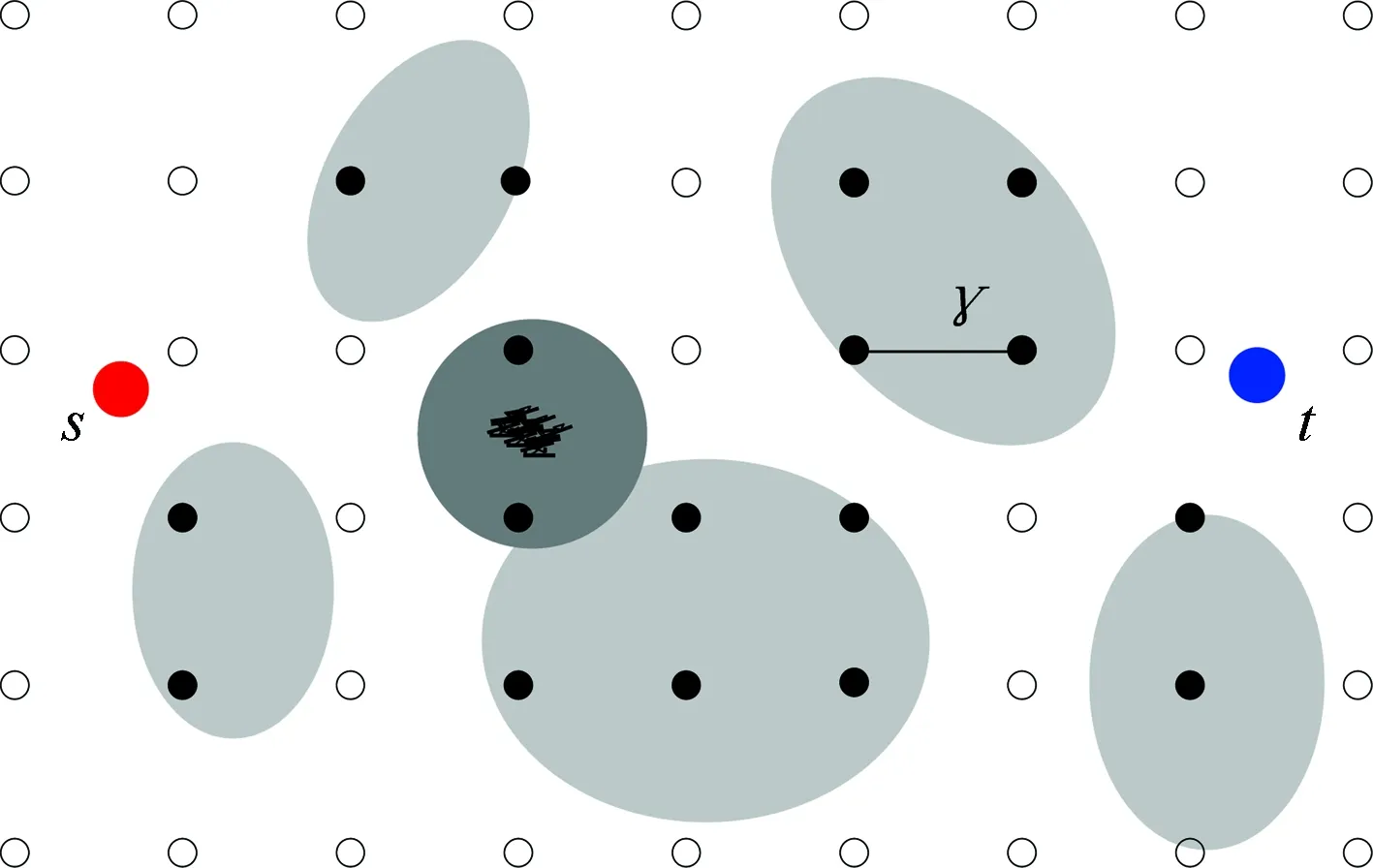
图1 空间离散化示意图Fig.1 Sketch map of spatial discretization

类似地，令T=[tij]|X|×|X|,其中tij为从xi飞行到xj的最短到达时间。为了降低求解的难度和不失研究重点，本文在假设无人机飞行速度v相同且不考虑无人机动力学特性基础上，采用如下方法估计tij值：从xi到xj的最短飞行路径包括两种情形：① 从xi到xj不穿越任何类型障碍和威胁覆盖区域的视线路径；② 由于从xi到xj的视线路径上存在地形障碍或敌方防空威胁而经过其他点xw∈X的折线路径。对任意xi,xj∈X,令tij=∞,通过下述两个步骤计算tij。

步骤1估计存在视线路径的所有xi、xj间的最短到达时间:

(12)

式中：‖xi,xj‖为从xi到xj的欧式距离。

步骤2基于步骤1的结果，通过Floyd算法[28]计算任意从xi到xj的估计最短到达时间。

空间离散化可事先利用已获取的环境信息和无人机最大通信距离信息完成，一旦给出s和t位置、可用作中继的无人机及初始位置信息，即可快速求解出中继节点布置结果N*。

3 多项式时间中继节点布置算法

空间离散化完成后，本文RNP问题求解复杂度仍然NP-hard。考虑到战场环境下快速决策需求，本节建立了一种能够满足多项式时间的中继节点布置算法,在满足此要求前提下，能够给出本文RNP问题接近最优的解。算法具体可分为两个阶段;第1阶段决策出需要使用的中继无人机的最少数量和中继链路各跳(hop)所能包含的可行布置点集合;第2阶段通过贪婪策略优先满足最难以到达的跳来减小构建中继链路花费的时间。

3.1 PTRPA算法第1阶段(PTRPA-Stage 1)

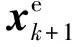
算法伪代码见表1。

定理1PTRPA-Stage 1保证了中继链路跳数最少(即使用的无人机数量最少)。

证明令G=(X,C),则G为无向无权图，文献[29]中已证明，通过BFS搜索到的G中从节点s到t的路径一定为最短路径，即对应本文中的中继跳数。定理1得证。

定理2经过PTRPA-Stage 1，不存在经过其他可行布置点xw∈X且xw∉L使跳数最少的链路。

证明假设存在这样一条链路w,根据定理1，易知该链路跳数为|L|-1。不妨假设xw为w中从s到t的第i跳，即图G中通过BFS从s经过i跳必然能搜索到xw,因此经过表1中步骤4～步骤13，xw必然在L中。接下来只要证明步骤14～步骤20没有将xw从L中删除，即可说明经过PTRPA-Stage 1，必有xw∈L,与假设矛盾。链路w中跳数为|L|-1,xw是从s到t的第i跳，那么从xw通过BFS经过|L|-1-i跳必然能够搜索到节点t,由于G为无向图，那么从t通过BFS经过|L|-1-i跳也必然能够搜索到节点，因此xw不会从L中被删除。定理2得证。

本阶段算法基于BFS方法，从所有可行布置点中，选择出在最少中继无人机数量要求下的每跳所有可能的布置点。考虑到每跳中可能包括多个可能布置点，以及对应不同的中继无人机可能带来不同的到达时间，因此还需进一步明确每跳布置点及对应的中继无人机。

表1 PTRPA算法第1阶段伪代码Table 1 Pseudo code of PTRPA-Stage 1

3.2 PTRPA算法第2阶段(PTRPA-Stage 2)

在PTRPA第1阶段结果基础上，确定每跳的唯一布置点及对应的无人机。令δ={0}k×1表示li(i=1,2,…,k)尚未确定唯一中继布置点，η={0}m×1表示无人机ui(i=1,2,…,m)未被选为中继节点，重复执行以下步骤，直到δi=1(i=1,2,…,k):

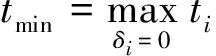
该阶段算法的伪代码见表2。

本阶段算法通过优先满足最难到达的跳的策略确定了各跳中的唯一布置点及对应的中继无人机，这是一种按步寻求局部最优的贪婪策略，最终结果可能无法全局最优，因为每次决策没有能够从全局考虑所有可能“布置点-无人机”对应方案。仿真实验表明，PTRPA最终给出的结果接近全局最优，而花费的计算却远小于全局寻优算法。

PTRPA算法第1阶段在找到t点并去除无效布置点后或搜索完X中所有布置点即终止，算法第2阶段在执行|L|-2次后即终止，PTRPA算法最终只给出唯一中继布置求解结果“N*”或“无法构建有效链路”。

一旦无人机获得中继布置点位置，即可采用A*、人工势场等方法[30]规划安全且满足自身动力学特性的可飞航迹，并控制自身飞向中继布置点。

表2 PTRPA算法第2阶段伪代码Table 2 Pseudo code of PTRPA-Stage 2

3.3 计算复杂度分析

PTRPA第1阶段基于BFS算法，算法复杂度为O(|X|2)[29]，其中X为所有可行布置点集合。PTRPA第2阶段步骤5～步骤8找局部最难到达的跳的复杂度不超过O(‖L‖m+|L|),此处令‖L‖表示L中包含的所有可行布置点数目，步骤10的复杂度不超过O(‖L‖2),步骤4～步骤11最多重复m次，因此PTRPA第2阶段复杂度不超过O(m(‖L‖m+|L|+‖L‖2))。PTRPA算法总时间复杂度为

O(|X|2)+O(m(‖L‖m+|L|+‖L‖2)≈

O(|X|2+m‖L‖2+m2‖L‖)

(13)

容易得出，本文PTRPA是一种多项式时间算法，考虑到一般情况下，无人机的使用数量远远少于战场区域中可行布置点的数量，因此整体上PTRPA算法的复杂度约为O(|X|2)。据此推测算法花费的计算时间受可用中继无人机数量影响很小，而受可行布置点数量的影响较大，第4节将通过仿真来验证推测的正确性。

4 仿真与分析

本节中，通过仿真实验验证算法的可行性、研究不同因素对算法性能的影响，并与其他算法进行对比分析。仿真平台的CPU为酷睿i7-3770，3.4 GHz，仿真软件为MATLAB R2015b。

4.1 算法可行性验证

检验PTRPA算法是否能够给出中继节点布置问题(11)的可行解。设置仿真区域长宽均为30 km，可行布置点间距为1 km，无人机最大通信距离为8 km，无人机飞行速度为50 m/s，待中继的节点位置坐标见表3，区域存在的地形障碍和敌方防空威胁见表4，可用作中继节点的无人机集合见表5。

表3 待中继作战节点位置Table 3 Position of combat node to be relayed

仿真结果如图2所示，其中，浅灰色区域表示地形障碍覆盖区域，深灰色区域表示敌方防空威胁覆盖区域，绿色‘×’表示可用中继无人机初始位置，红色‘+’表示PTRPA算法给出的中继布置位置点，蓝色实线表示用于估计最短到达时间的简化航路，青色实线表示构建的中继通信链路。各中继布置点位置及对应的无人机见表6。

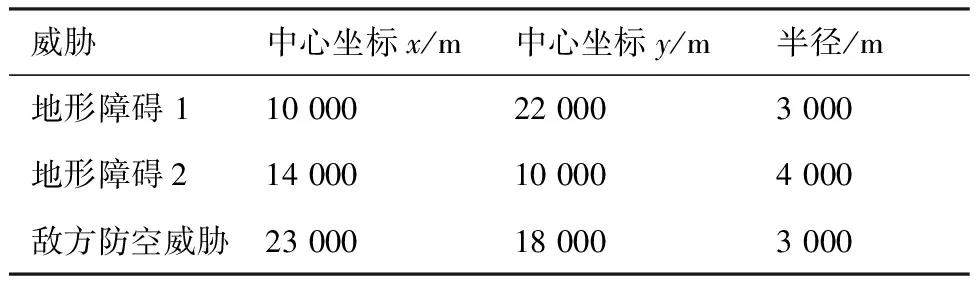
表4 地形障碍及敌方防空威胁参数

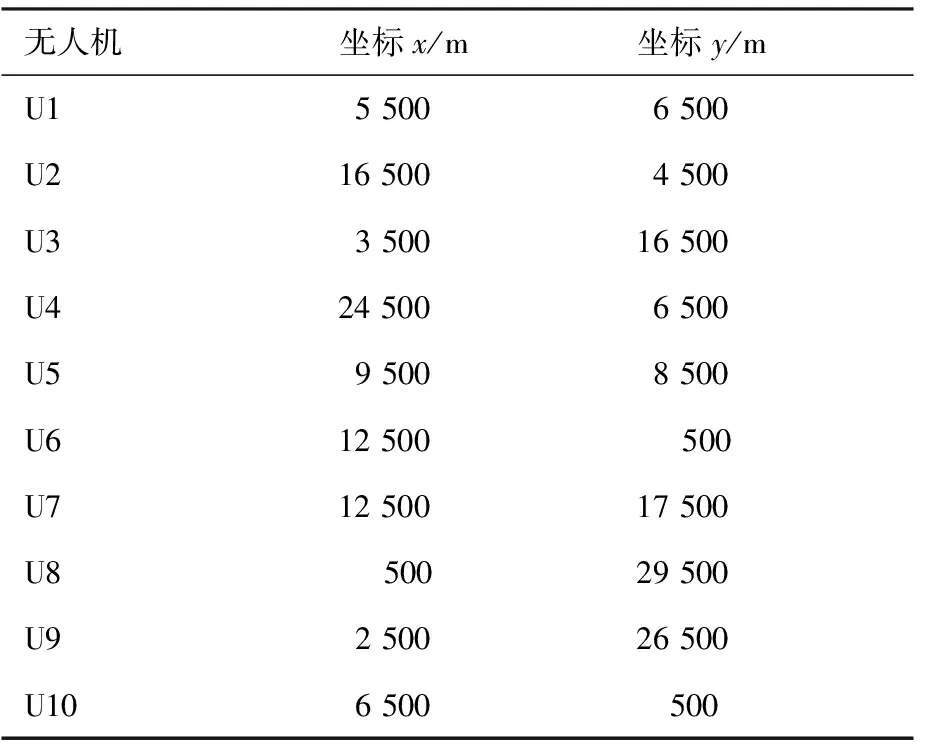
表5 中继无人机初始位置Table 5 Initial position of relay UAVs

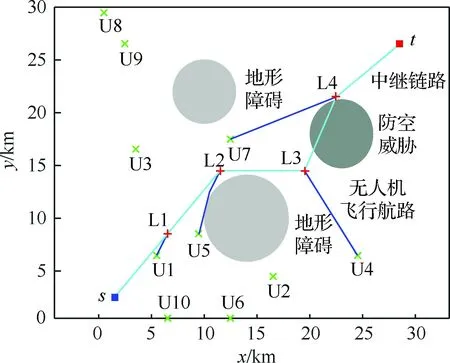
图2 中继无人机布置结果示意图Fig.2 Sketch map of result of relay UAV placement

表6 中继无人机布置结果Table 6 Results of relay UAV placement

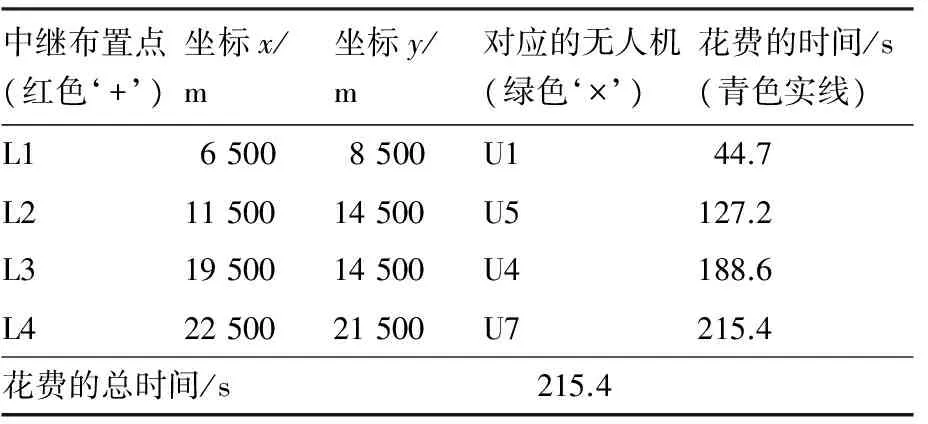
中继布置点(红色‘+’)坐标x/m坐标y/m对应的无人机(绿色‘×’)花费的时间/s(青色实线)L165008500U144．7L21150014500U5127．2L31950014500U4188．6L42250021500U7215．4花费的总时间/s215．4

为实现点s和t间的有效通信，至少需要布置4架无人机作为中继。图2中：① 距离中继布置点L2最近的无人机为U7，然而实际是由无人机U5飞往L2，而U7飞往L4，这是因为只有当所有中继无人机均到达对应的中继布置点时，中继链路才能发挥功能；② 中继链路s-L1-L2-L3-L4-t中任意相邻节点间视线通信路径均避开了地形障碍，而L3-L4却穿越了敌方防空威胁覆盖区域； ③ RNP问题给出的中继链路s-L1-L2-L3-L4-t显然不是从s到t最短可飞航路。

通过该仿真实验，验证了本文建立的RNP问题模型和给出的PTRPA算法能够在无法直接通信的两点间通过布置多架无人机作为中继来实现有效中继链路的构建。

4.2 考虑构建中继链路花费时间必要性验证

为了进一步验证本文考虑构建中继链路花费最短时间的必要性，与以链路质量(通过链路容量[25](Link Capacity)来评价)和最小无人机数量为目标函数的中继布置结果(图3)比较，其中，参数设定同4.1节，结果见表7。

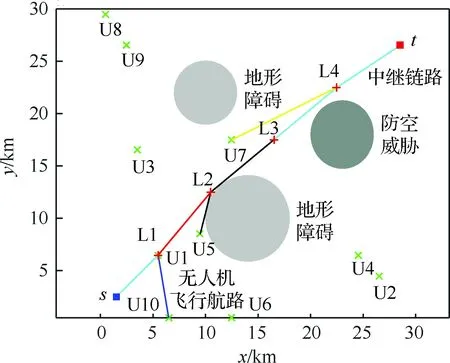
图3 最大链路容量下的中继布置结果示意图Fig.3 Sketch map of result of relay UAV placement by optimizing link capacity

表7 最大链路容量下中继无人机布置结果

Table 7 Results of relay UAV placement byoptimizing link capacity

中继布置点(红色‘+’)坐标x/m坐标y/m对应的无人机花费的时间/sL155006500U10121．66L21050012500U1156．22L31650017500U5238．70L42250022500U7223．62花费的总时间/s238．70

与表6数值对比发现，最优链路质量指标下中继布置点位置和对应的中继无人机均发生了变化，且最短需要花费238.7 s才能完成链路构建，而在本文模型和算法下，最短只需要215.4 s即可完成链路组建，少花费23.3 s(约10%)时间，而这在战场应急情形下，可能非常重要。验证了RNP建模时有必要考虑构建中继链路花费的时间。

4.3 中继布置结果对比与分析

本文建立的RNP问题(11)是难以求解的整数多目标优化问题(离散化处理后)，且目标函数难以同时最优，本节在最小化无人机数量条件下，从中继布置结果和算法时间性能两个方面对比分析PTRPA算法与以下两种算法的性能：

1) 随机抽样方法[31](Stochastic Sample, SS)。该方法在求解空间内随机的选取可行解，求取这些解中构建中继链路花费时间最少的解。

2) 遗传算法[32](Genetic Algorithm, GA)。遗传算法是一种随机进化算法，通过模拟生物遗传的方式，将问题的可行解通过编码的方式表示为遗传的载体，即染色体，每条染色体表示一个个体，即问题的一个解，多个个体组成种群，基于适者生存、优胜劣汰的原则，使用选择、交叉、变异算子不断生成新的种群，使得种群不断趋向获取问题的最优解。算法借助于gatbx工具箱，采用排序选择、单点交叉和单点变异算子。

基于Monte-Carlo方法重复100组实验对比与分析不同因素对PTRPA、SS和GA算法构建中继布置平均花费的最短时间的影响，实验中每次随机给出无人机的初始位置及待中继点s和t的位置，仿真区域、无人机飞行速度和防空威胁、地形障碍设置同前，SS算法初始解规模为500。具体包括：

1) 无人机数量对构建中继链路花费的最短时间的影响，设置布置点间距为1 km、无人机最大通信距离为8 km，结果如图4(a)所示。

从图4(a)中可以看出，随着无人机数量的增长，构建中继链路花费的最短时间不断减小，这是由于随着无人机的增多，无人机更有可能分布在最优中继布置点附近。另外，在无人机数量较少的情况下，GA和PTRPA算法给出的结果性能接近，GA结果稍优于PTRPA；而当无人机数量增多时，由于GA遗传代数的限制，PTRPA往往能够更稳定地给出性能更优的解，而SS算法性能明显不足，不宜采用。

2) 无人机最大通信距离对构建中继链路花费的最短时间的影响，设置无人机数量为10、布置点间距为1 km，结果如图4(b)所示。

从图4(b)可以看出，随着无人机通信能力的增强，构建中继链路花费的最短时间不断减小，这是由于无人机可以飞至相对较近的位置点即可完成有效中继链路构建，且本文的PTRPA算法能够给出与GA算法性能相近的结果。

3) 布置点间距对完成中继布置花费的最短时间的影响，设置无人机数量为10、最大通信距离为8 km，结果如图4(c)所示。

从图4(c)可以看出，随着空间离散过程中布置点间距缩小，构建中继链路花费的最短时间减少，这是由于随着离散布置点间距的减小，离散域内最优中继布置点位置更趋近于连续域内最优中继布置点位置。

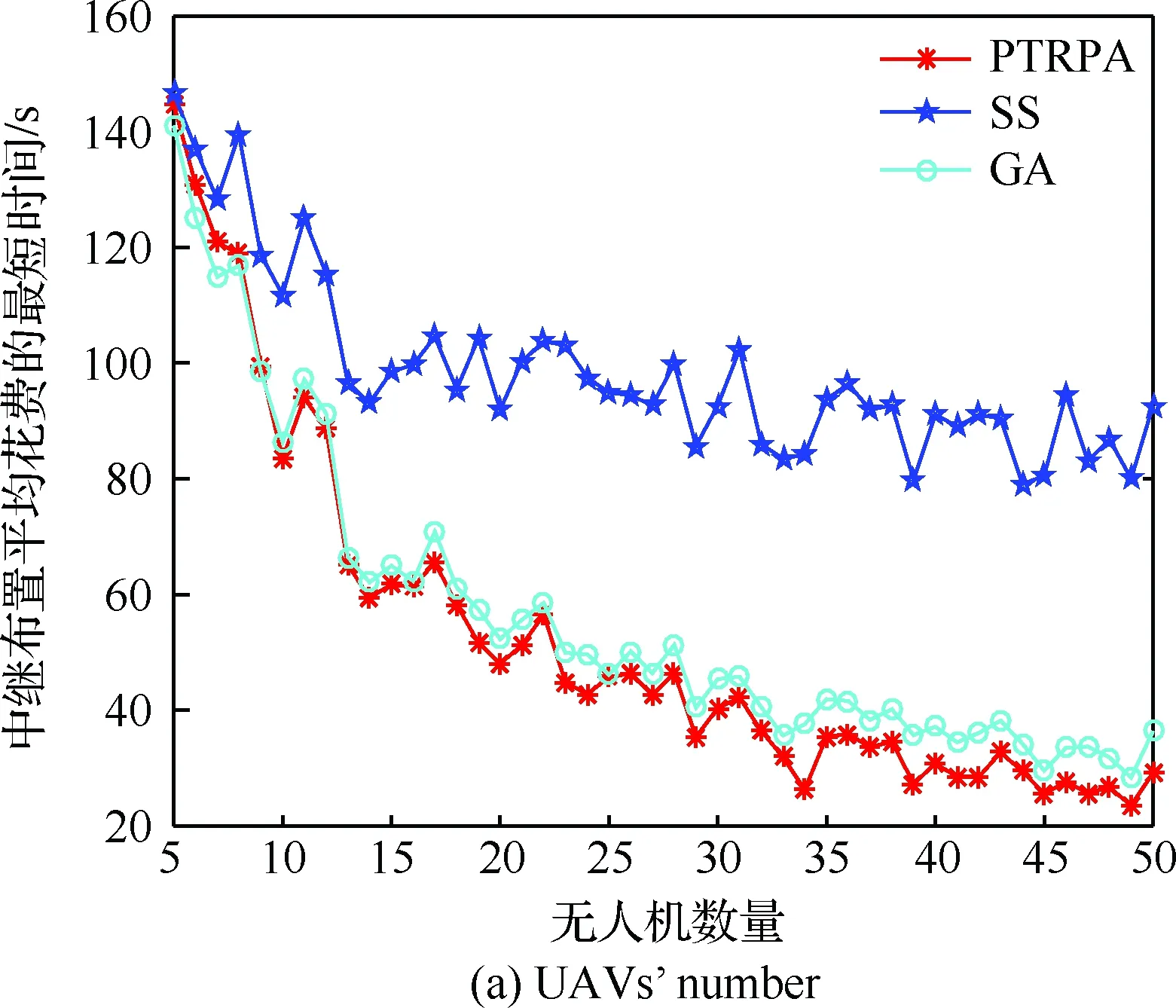
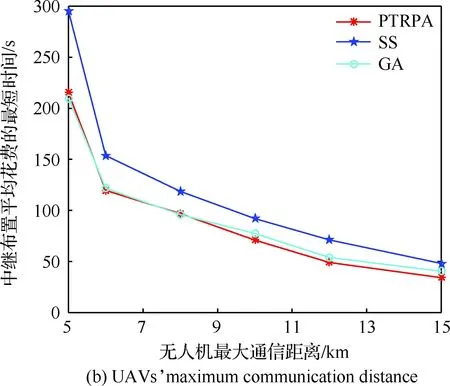
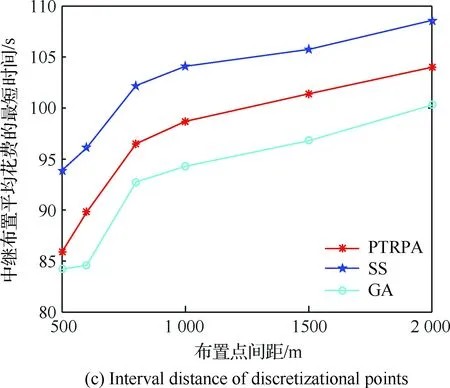
图4 无人机数量、无人机最大通信距离以及布置点间距对构建中继链路花费的最短时间的影响Fig.4 Influence of UAVs’ number,UAVs’ maximum communication distance and interval distance of discretizational points on average relay placement time

综合本节仿真结果来看，PTRPA算法给出的中继布置结果性能与最优结果性能接近，可满足使用要求，接下来继续讨论算法时间性能是否满足战场快速决策要求。

4.4 算法时间性能对比与分析

从算法复杂度来看，使用SS和GA算法求解本文基于多无人机的中继布置问题的时间复杂度分别为O(|X|2+mS‖L‖)和O(|X|2+g(S2+mS‖L‖)),其中g为遗传代数，S为初始规模。通常‖L‖≥m,种群规模不少于20，遗传代数不少于50，于是‖L‖通常小于gS,因此通常GA算法花费的计算时间比PTRPA算法花费的计算时间多；当S>‖L‖时，SS算法的花费的计算时间较多，而为了保证解的质量，通常会取较大S值。综上，通常情况下，PTRPA算法时间性能要优于GA和SS算法时间性能。

接下来基于Monte-Carlo方法重复进行100组实验对比并分析不同因素对PTRPA，SS和GA算法花费的平均时间的影响，以检验算法的时间性能。实验中每次随机给出无人机的初始位置及待中继点s和t的位置，仿真区域、无人机飞行速度、地形障碍和敌方防空威胁设置同前。设置GA初始种群规模为100，遗传代数为200；设置SS初始解规模为500。具体包括：

1) 无人机数量对算法花费的时间的影响，设置布置点间距为1 km、无人机最大通信距离为8 km，结果如图5所示。

从图5可以看出，无人机数量对算法花费的时间的影响几乎可以忽略，PTRPA算法的时间性能要明显强于GA算法，略优于SS算法，且PTRPA算法花费的时间始终控制在毫秒级，满足战场决策实时性要求。

然而根据算法分析，PTRPA算法第2阶段时间复杂性为O(m(‖L‖m+|L|+‖L‖2)),无人机数量的增加会导致求解空间增大，算法花费的时间应该呈现增长的趋势。单独讨论无人机数量增长对PTRPA算法第2阶段花费的时间的影响结果如图6所示，与理论分析符合。

2) 无人机最大通信距离对算法花费的时间的影响，设置无人机数量为10、布置点间距为1 km，结果如图7所示。

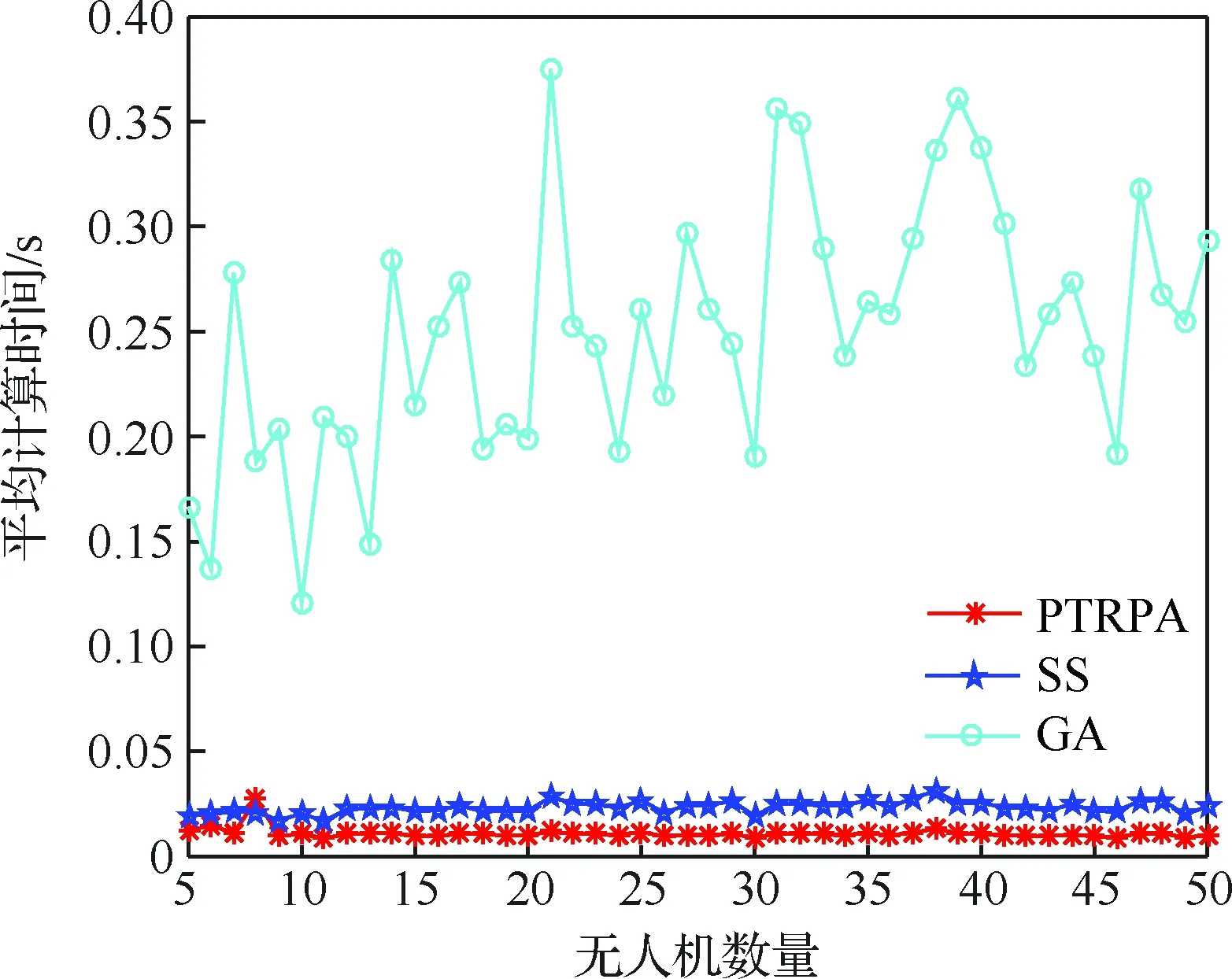
图5 无人机数量对算法花费的计算时间的影响Fig.5 Influence of UAVs’ number on average computation time cost of algorithm

图6 无人机数量对PTRPA第2阶段花费的平均 计算时间的影响Fig.6 Influence of UAVs’ number on average computation time cost of PTRPA-Stage 2

图7 无人机最大通信距离对算法花费的计算时间 的影响Fig.7 Influence of UAVs’ maximum communication distance on average computation time cost of algorithm

从图7可以看出，无人机通信能力对算法花费的计算时间影响几乎可以忽略，这是因为随着无人机通信能力增强，需要使用的中继跳数变少，即|L|变小，而PTRPA算法时间复杂度为O(|X|2+m(‖L‖m+|L|+‖L‖2)),|L|对其影响几乎可以忽略。

3) 布置点间距对算法花费的时间的影响，设置无人机数量为10、最大通信距离为8 km，结果如图8所示。

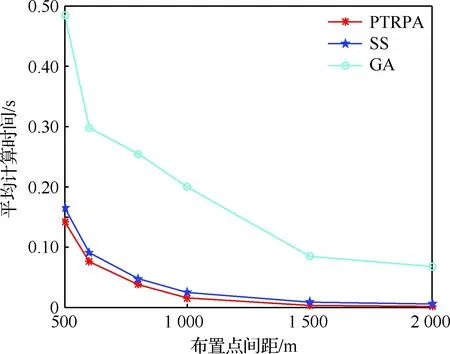
图8 布置点间距对算法花费的平均计算时间的影响Fig.8 Influence of interval distance of discretizational points on average computation time cost of algorithm

从图8可以看出，离散过程中增加离散布置点的间距，可以显著地提升算法的时间性能，这是因为布置点间距的增加，使得可行布置点数量减小，即|X|减小，同时PTRPA算法时间复杂度接近O(|X|2),|X|减小会导致花费的计算时间快速减小。另外，PTRPA算法的时间性能依然高效可靠。然而，考虑到布置点间距对算法性能的影响相对来说要大于其他因素，因此在空间离散化过程中，应当在满足需求的情况下，适当的增加布置点间距。

另外，综合图5和图7来看，无人机数量和无人机最大通信距离对算法的计算时间影响很小，这是因为|X|同时远大于|L|和m,因此在|X|不变情况下，|L|和m的对算法花费的总时间影响几乎可以忽略，仿真结果验证了3.3节预测“PTRPA算法花费的计算时间受可用中继无人机数量影响很小，而受可行布置点数量的影响较大”。同时本节仿真结果也验证了前文结论，PTRPA算法在时间性能上优于GA算法。另外，SS算法无论是时间性能，还是结果性能，都不如这二者，一般不可取。

4.5 中继布置成功率影响因素分析

前文讨论了不同因素对算法结果和时间性能的影响，然而中继布置的最基本要求是能够构建有效地通信链路，能否构建有效中继链路通信链路与无人机数量、无人机最大通信距离存在直接关系，而与问题的求解算法无关。本节旨在通过仿真实验给出实际应用中提升构建有效中继链路成功率的方法和建议，其中，中继布置能否成功的判断方法可参考PTRPA-stage的步骤21～步骤24，本文定义中继布置成功率为

中继布置成功率=

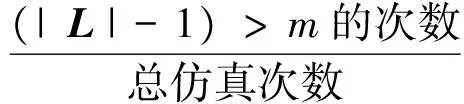
(14)

实验中，通信距离分别设置为2、5、8、11和14 km，每组进行1 000次仿真实验，其他参数设定同前，结果如图9所示。

分析图9给出的结果可以得出，使用尽可能多数量的无人机、尽可能大的提升无人机的通信能力，能够提升中继节点布置的成功率。尤其是在节点通信能力较差的情况下，必须要有足够的无人机可被用作中继节点。

图9 无人机数量和最大通信距离对中继节点 布置成功率的影响Fig.9 Influence of UAVs’ number and maximum communication distance on success ratio of relay node placement

5 结 论

1) 针对战场可能出现的紧急通信需求，建立了基于多无人机的中继节点布置问题模型，不但考虑了使用最少数量的中继无人机，同时考虑了在尽可能短的时间内完成中继链路构建。

2) 针对本文RNP问题是难以求解的NP-hard问题，给出了一种多项式时间中继节点布置算法(PTRPA)，并理论分析了算法的时间复杂度。

3) 通过与不考虑构建中继链路花费时间的方法的对比仿真表明，本文建立的RNP模型确实能够在更短的时间内完成有效中继链路构建。且通过仿真对比不同因素对PTRPA、遗传算法和随机抽样算法的结果性能和时间性能影响，验证了PTRPA算法不但能够给出接近最优的解，且更加快速，可以满足战场决策需求。

[1] GOLDSMITH A. Wireless communication[M]. New York: Cambridge University Press, 2005: 24-53.

[2] RANGA V, DAVE M, VERMA A K. Relay node placement to heal partitioned wire less sensor networks[J]. Computers and Electrical Engineering, 2015, 48: 371-388.

[3] CALINESCU G. Relay placement for two-connectivity[J]. Discrete Optimization, 2014, 14(14): 17-33.

[4] CHANDRASHEKAR K, DEKHORDI M R, BARAS J S. Providing full connectivity in large ad hoc networks by dynamic placement of aerial platforms[C]∥Proceedings of IEEE Military Communication Conference.Piscataway,NJ: IEEE Press, 2004: 1429-1436.

[5] LANZA-GUTIERREZ J M, GOMEZ-PULIDO J A, VEGA-RODRIGUEZ M A. A trajectory algorithm to solve the relay node placement problem in wireless sensor net-works[C]∥2nd International Conference on the Theory and Practice of Natural Computing. Berlin: Springer-Verlag Berlin Heidelberg，2013: 145-156.

[6] 陆克中, 刘刚, 陶耀东, 等. 无线传感器网络中继节点的最小功耗布置算法[J]. 小型微型计算机系统, 2011, 32(6): 1035-1040.

LU K Z, LIU G, TAO Y D, et al. Algorithm of minimum power relay node placement in wireless sensor networks[J]. Journal of Chinese Computer Systems, 2011, 32(6): 1035-1040 (in Chinese).

[7] YANG P, YANG L, XUE Y, et al. On the optimum placement and number selection of relay nodes in multi-hop routing for minimizing communication power con-sumption[M]∥WANG R, XIAO F. Advances in Wireless Sensor Networks. Berlin: Springer, 2012: 598-612.

[8] BHATTACHARYA A, RAO A, NAVEEN K P, et al. QoS constrained optimal sink and relay placement in planned wireless sensor networks[C]∥International Conference on Signal Processing and Communications (SPCOM).Berlin: Springer, 2014.

[9] LANZA-GUTIERREZ J M, GOMEZ-PULIDO J A, VEGA-RODRIGUEZ M A, et al. A parallel evolutionary approach to solve the relay node palcement problem in wireless sensor networks[C]∥Proceedings of the 15th Annual Conference on Genetic and Evolutionary Computation. New York: ACM, 2013: 1157-1164.

[10] CHEN G, CUI S. Relay node placement in two-tiered wireless sensor networks with base stations[J]. Journal of Combinatorial Optimization, 2013, 26(3): 499-508.

[11] HAN B, LI J, SU J. Optimal relay node placement for multi-pair cooperative communication in wireless networks[C]∥Proceedings of IEEE Wireless Communications and Networking Conference.Piscataway,NJ: IEEE Press, 2013: 4724-4729.

[12] ISLAM M, DZIONG Z, SOHRABY K, et al. Capacity-optimal relay and base station placement in wireless networks[C]∥The International Conference on Information Networking.Piscataway,NJ: IEEE Press, 2012: 358-363.

[13] BURDAKOV O, DOHERTY P, HOLMBERG K, et al. Optimal placement of UV-based communication relay nodes[J]. Journal of Global Optimization, 2010, 48(4): 511-531.

[14] RUBIN I, ZHANG R H. Placement of UAVs as communication relays aiding mobile Ad Hoc wireless networks[C]∥Proceedings of IEEE Military Communications Conference MILCOM. Piscataway, NJ: IEEE Press, 2007.

[15] 郑锴, 童利标, 陆文骏. 应用无人机实现地面无线传感器网络通信中继的探讨[J]. 现代电子技术, 2007, 23: 40-50.

ZHENG K, TONG L B, LU W J. Discussion on the communication relay of the wireless ground sensor network by using UAV[J]. Modern Electronics Technique, 2007, 23: 40-50 (in Chinese).

[16] 朱秋明, 周生奎, 霍帅珂, 等. 无人机中继平台区域覆盖统计模型[J]. 航空学报, 2014, 35(1): 223-229.

ZHU Q M, ZHOU S K, HUO S K, et al. A statistical area coverage model for unmanned aerial vehicles as relay platforms[J]. Acta Aeranautica et Astronautica Sinica, 2014, 35(1): 223-229 (in Chinese).

[17] 欧阳键, 庄毅, 薛羽. 非对称衰落信道下无人机中继传输方案及性能分析[J]. 航空学报, 2013, 34(1): 130-140.

OUYANG J, ZHUANG Y, XUE Y. UAV relay transmission scheme and its performance analysis over asymmetric fading channels[J]. Acta Aeranautica et Astronautica Sinica, 2013, 34(1): 130-140 (in Chinese).

[18] BURDAKOV O, DOHERTY P, HOMBERG K, et al. Relay positioning for unmanned aerial vehicle surveillance[J]. International Journal of Robotics Research, 2010, 29(8): 1069-1087.

[19] HAN Z, SWINDLEHURST A L, LIU K J R. Optimization of MANET connectivity via smart deployment & movement of unmanned aerial vehicles[J]. IEEE Transactions on Vehicular Technology, 2009, 58(7): 3533-3546.

[20] BOSKOVIC J D, PRASANTH R, MEHRA R K. A multi-player autonomous intelligent control architecture for unmanned aerial vehicles[J]. Journal of Aerospace Computing, Information, and Communication, 2014, 1(12): 605-629.

[21] LAWLER E L. Combinatorial optimization: networks and matroids[M]. New York: Library of Congress Catalging in Publication Data, 1976: 182-214.

[22] 雷德明, 严新平. 多目标智能优化算法及其应用[M]. 北京: 科学出版社, 2009.

LEI D M, YAN X P. Multi-objective intelligent optimization algorithms and its application[M]. Beijing: Science Publication, 2009 (in Chinese).

[23] MANATHARA J G, SUJIT P B, BEARD R W. Multiple UAV coalition formation for a search and prosecute mission[J]. Journal of Intelligent and Robotic Systems, 2011, 62(1): 125-158.

[24] GEORGE J M, SUJIT P B, SOUSA J B. Coalition formation with communication delays and maneuvering targets[C]∥AIAA Guidance, Navigation, and Control Conference. Reston, VA: AIAA, 2010.

[25] DIXON C, FREW E W. Optimizing cascaded chains of unmanned aircraft acting as communication relays[J]. IEEE Journal on Selected Areas in Communication, 2012, 30(5): 883-898.

[26] KOPEIKIN A, PONDA S, HOW J P. Control of communication networks for teams of UAVs[M]∥VALAVA-NIS K P, VACHTSEVANOS G J. Handbook of Unmanned Aerial Vehicles. Berlin: Springer, 2015: 1619-1654.

[27] YAN Y, MOSTOFI Y. Robotic router formation in realistic communication environments[J]. IEEE Transactions on Robotics, 2012, 28(4): 810-827.

[28] 王桂平, 王衍, 任嘉层. 图论算法理论、实现及应用[M]. 北京: 北京大学出版社, 2011: 131-192.

WANG G P, WANG Y, REN J C. Graph theory, implementation and application[M]. Beijing: Peking University Press, 2011: 131-192 (in Chinese).

[29] CORMEN T H, LEISERSON C E, RIVEST R L, et al. Introduction to algorithm[M]. 3rd ed. Cambridge: MIT Press, 2009: 589-64.

[30] 姚远, 周兴社, 张凯龙, 等. 基于稀疏A*搜索和改进人工势场的无人机动态航迹规划[J]. 控制理论与应用, 2010, 27(7): 953-959.

YAO Y, ZHOU X S, ZHANG K L, et al. Dynamic trajectory planning for unmanned aerial vehicle based on sparse A* search and improved artificial potential field[J]. Control Theory and Applications, 2010, 27(7): 953-959 (in Chinese).

[31] 金畅. 蒙特卡洛方法中随机数发生器和随机抽样方法的研究[D]. 大连: 大连理工大学, 2006.

JIN C. Study on random number generator and random sampling in Monte Carlo method[D]. Dalian: Dalian University of Technology, 2006 (in Chinese).

[32] 雷英杰, 张善文. MATLAB遗传算法工具箱及应用[M]. 2版. 西安: 西安电子科技大学出版社, 2014: 62-105.

LEI Y J, ZHANG S W. MATLAB genetic algorithm toolbox and its application[M]. 2nd ed. Xi’an: Xidian University Press, 2014: 62-105 (in Chinese).

Modelingandoptimizationmethodofrelaynodeplacement>usingmulti-UAV

WUGaofeng,GAOXiaoguang*,FUXiaowei

SchoolofElectronicsandInformation,NorthwesternPolytechnicalUniversity,Xi’an710072,China

Inthebattlefieldenvironment,arelaycommunicationchainisurgentlyneededtobeformedbetweentwonodeswhichareunabletocommunicate.Inthispaper,UnmannedAerialVehicles(UAVs)areusedasrelaynodes,andamodelforrelaynodeplacementisgiven.TheobjectivefunctionsaretheminimumnumberofrequiredrelayUAVsandtheminimumtimecostforformingtherelaychain,andtheconstraintsarethesafetyofUAVsandtheeffectivenessoftherelaychain.Sincetheproblemismixedintegermulti-objectiveoptimizationwhichisknownhardtobesolved,andtherequirementforquickandeffectivedecisionisurgentlyneeded,aPolynomialTimeRelayPlacementAlgorithm(PTRPA)isgiventosolvetheproblemfastandprovideasub-optimalsolution.Thefeasibilityandeffectivenessofthealgorithmisvalidatedwithsimulation,andtheimpactsofdifferentfactorsonthealgorithmisstudiedwiththeMonte-Carlomethod.Theresearchfiguresoutanewrelaynodeplacementscenariointhecomingnetworkedwarfare,andprovidesareferablemodelingandsolvingmethod.

UnmannedAerialVehicle(UAV);relay;wirelesscommunication;nodeplacement;polynomialtimealgorithm;multi-objectiveoptimization

2017-02-27；Revised2017-06-14；Accepted2017-07-17；Publishedonline2017-07-311048

URL：http://hkxb.buaa.edu.cn/CN/html/20171123.html

NationalNaturalScienceFoundationofChina(61573285)

.E-mailcxg2012@nwpu.edu.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.321195

V279；TP2

A

1000-6893(2017)11-321195-13

2017-02-27；退修日期2017-06-14；录用日期2017-07-17；< class="emphasis_bold">网络出版时间

时间：2017-07-311048

http://hkxb.buaa.edu.cn/CN/html/20171123.html

国家自然科学基金(61573285)

.E-mailcxg2012@nwpu.edu.cn

吴高峰，高晓光，符小卫.一种基于多无人机的中继节点布置问题建模与优化方法J． 航空学报,2017,38(11):321195.WUGF,GAOXG,FUXW.Modelingandoptimizationmethodofrelaynodeplacementusingmulti-UAVJ.ActaAeronauticaetAstronauticaSinica,2017,38(11):321195.

(责任编辑：苏磊)