嵌套阵列最大似然估计测向算法
陈璐,毕大平,崔瑞,韩佳辉
1.电子工程学院,合肥 230037 2.安徽省电子制约技术重点实验室,合肥 230037
嵌套阵列最大似然估计测向算法
陈璐1,*,毕大平1, 2,崔瑞1,韩佳辉1
1.电子工程学院,合肥 230037 2.安徽省电子制约技术重点实验室,合肥 230037
针对在辐射源个数未知的条件下嵌套阵列难以估计多个辐射源角度的问题,提出了基于最大似然估计(MLE)的嵌套阵列角度估计算法。算法在嵌套阵列模型的基础上,首先通过推导阵列截获多辐射源信号的最大似然函数及其梯度,利用最速下降法估计出空域中所有潜在辐射源的角度;然后,通过多元假设检验,利用最大似然比与门限进行比较,确定出空域中所有潜在辐射源中某一时刻发射信号的活跃辐射源角度,排除其余噪声形成的虚假辐射源角度,解决了在辐射源个数未知条件下嵌套阵列对多个辐射源角度估计问题。仿真结果表明:与传统多重信号分类(MUSIC)算法相比,该算法在辐射源数目未知、存在相干信号、低信噪比(SNR)、低快拍数条件下,均具有较好的角度估计精度,并且算法形成的虚拟阵列自由度是空间平滑MUSIC算法的2倍;多元假设检验法比传统信源数目估计算法在低信噪比条件下和处理相干信号方面具有明显优势。
嵌套阵列;最大似然估计;角度估计;多元假设检验;信源数目
多辐射源角度估计一直是电子对抗领域研究的重难点问题,传统的角度估计方法主要基于均匀线性阵列提出的,均匀线阵(Uniform Linear Array,ULA)具有结构简单、测向误差小、分辨率高等优点[1],但由于空间采样Nyquist定理的限制,均匀线阵阵列间隔必需小于接收信号半波长,使得均匀阵列阵元间距较小,存在通道间串扰的问题,并且均匀线阵的测向自由度受阵元个数的限制[2],导致均匀线阵很难同时对空域中数目多于阵元数量的辐射源角度进行估计,为解决这一问题Moffet提出了最小冗余阵列理论[3],通过研究发现,在阵元个数相同时,利用非均匀阵列的布局形式能够有效提高自由度和测向分辨率。不同的非均匀阵列布局的形式能够适用不同的性能要求,提高了测向设备的灵活性[4-6]。
为进一步提高非均匀阵列的自由度,文献[7-8]在最小冗余阵的基础上,通过构造增广协方差矩阵,能够使原有的最小冗余阵自由度进一步提高。但是有限采样的增广协方差矩阵不是半正定的,因此不满足协方差矩阵的要求。文献[9-10]通过设计算法将增广协方差矩阵转化为正定的Toeplitz矩阵,然而算法的复杂度较高,影响了其在具体问题中的应用。文献[11]通过引入Khatri-Rao积运算对接收信号进行处理,将N个阵元的均匀阵列的自由度提高到了2N-1,但是这种方法要求信号为伪平稳信号,不能应用于平稳信号。在此基础上,文献[12]提出差分共阵的概念,通过对多级嵌套阵接收的信号进行Khatri-Rao积变换,构成自由度极高的虚拟阵列,在阵元数相同的前提下,差分共阵显著提高了传统均匀线阵的测向能力。然而文章中采用的测向算法为空间平滑多重信号分类(MUSIC)算法,空间平滑MUSIC算法使虚拟阵列的自由度损失了一半,同时对相干信号角度估计的效果较差[13-14]。
在文献[12]的基础上,为进一步提高阵列自由度,本文尝试通过最大似然算法进行多辐射源角度估计。无论是MUSIC算法还是最大似然估计算法,使用的前提条件是已知辐射源数目[15-16],在实际对非合作辐射源的处理中很难满足这一条件。文献[17]利用Manikas提出的自适应信号参数估计和分类(Adaptive Signals Parameter Estimation and Classification, ASPECT)算法[18],通过消除Pisarenko算法谐波分解过程中产生的伪峰,估计出信号角度信息的同时,判断出辐射源数目。该方法能够在辐射源数目未知的前提下估计角度信息,但是算法要求信噪比(Signal-to-Noise Ratio, SNR)较高且无法对相干信号进行处理。文献[19]在新的Capon波束形成优化框架下,提出了MUSIC-like算法,该算法能够在信源数目未知的前提下对角度信息进行估计,但算法要求在每个方向上进行扫描都要计算广义特征值,导致算法计算量较大,并且无法处理相干信号。本文在嵌套阵列框架下,研究信源个数未知并存在相干信号条件下的多辐射源角度估计问题。传统的最大似然估计算法多数采用交替投影进行求解,交替投影的前提是已知辐射源数目,因此,无法利用交替投影法求解。本文通过对嵌套阵列的最大似然函数进行求解,推导出了最大似然函数梯度的封闭表达式,利用最速下降法对空域中所有潜在辐射源角度信息进行估计,然后利用多元假设检验的方法找出所有潜在辐射源中某一时刻的活跃辐射源,排除噪声形成的虚假辐射源,从而实现在辐射源数目未知条件下利用嵌套阵列对空域中多个活跃辐射源进行同时测向,并且形成的虚拟阵列是文献[12]的虚拟阵列自由度的2倍。仿真表明本文提出的方法能够在低信噪比条件下实现对相干信号多辐射源测向,且性能优于传统测向算法。
1 嵌套阵列模型

(1)
式中:Sin为第i级第n个阵元位置。其阵列自由度为可表示为
(2)
表明嵌套阵列能够有效提高阵列识别信号源的数量。

图1 嵌套阵列结构图Fig.1 Structure of nested array
2 多辐射源信号模型
假设空域中存在K个相互独立的潜在辐射源从θ=[θ1,θ2,…,θK]个方向(θ为入射信号与阵列法线的夹角,如图1),某一时刻t,有K0(K0≤K)个辐射源向M级嵌套阵元发射信号,这K0个辐射源被称为这一时刻的活跃辐射源,且数目未知,其他K-K0个辐射源被称为这一时刻的非活跃辐射源。
由于t时刻活跃辐射源数目未知,将K个潜在辐射源均视为活跃辐射源,则阵列输出为[23]
x(t)=A(θ)s(t)+n(t)
(3)

由于信号源之间相互独立,信号源s(t)的协方差矩阵为Rss=diag{ρ1,ρ2,…,ρK},其中ρk为第k个信号源的功率。则接收信号x(t)的协方差矩阵为
Rxx=E{x(t)xH(t)}=
A(θ)E{s(t)sH(t)}AH(θ)+E{n(t)nH(t)}=
(4)
向量化Rxx可得
(5)

(6)

(7)
新的虚拟阵列能够有效地扩展原有阵列的孔径,提高阵列自由度。p=[ρ1,ρ2,…,ρK]T,是由辐射源信号功率组成的矢量,将其作为虚拟阵列的输入信号矢量,可以视为K个全相干信号。对全相参信号进行角度估计,经典MUSIC算法无法实现,空间平滑MUSIC算法会使虚拟阵列自由损失一半[12],最大似然估计算法是解决这一问题的常用方法。交替投影法常被用来求解最大似然函数角度估计问题,但隐含条件为已知辐射源个数,在辐射源个数未知条件下,该方法无法求解最大似然函数角度估计(Maximum Likelihood Estimation, MLE)问题。
3 最速下降法最大似然函数角度估计
将空域中所有潜在K个辐射源作为测向目标,推导虚拟阵列的最大似然函数和梯度。
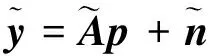
(8)
则由虚拟阵元组成的新阵列接收的数据矢量满足概率密度函数
(9)

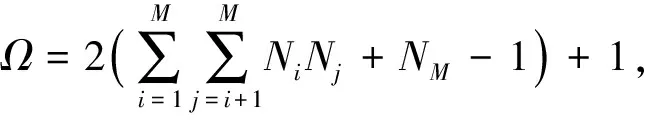
(10)
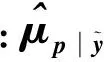
(11)
对式(11)取对数得
(12)
(13)
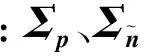
(14)
式中:均值和方差满足(详细推导见附录A)
(15)
(16)
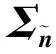
(17)
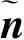
(18)
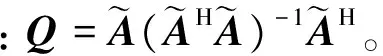
(19)
将均值和方差代入式(12),可以变为
(20)
根据Sylvester恒等行列式,可得
(21)
根据Woodbury定理,可得
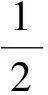
(22)
将式(21)和式(22)代入式(20),可化简为
(23)
忽略常量因子可得
(24)
因此,对多个辐射源角度估计值为

(25)
利用最速下降法对式(25)进行求解可得
(26)
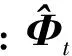
(27)
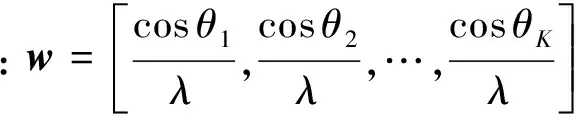
文献[12]中采用前向空间平滑MUSIC算法,要求平滑的子阵列阵元数要大于信号数目,文章中的平滑子阵列阵元数为Ω/2,因此最多估计Ω/2个信号源方向,导致仅利用了虚拟阵列自由度的一半。通过式(26)可以得到K个辐射源角度,最大似然估计方法能够估计Ω个方向辐射源角度。根据最速下降法在K个方向上求得K个角度,其中仅包含K0个活跃辐射源,其他K-K0个角度为噪声形成的虚假角度,下面通过多元假设检验的方法找出K0个活跃辐射源角度。
4 信源数目估计
传统的最大似然估计测向方法需要首先通过信息论、盖氏圆、矩阵分解等方法确定信号源数目,然后利用交替投影等方法估计信号源角度,本文提出的多元假设检验算法可以有效避免信号源数目估计这一繁琐运算,通过下面的方法直接估计出活跃信号源角度。
假设空域中存在K个信号源,K值的大小由先验信息获得,为空域中所有可能辐射源数目之和,嵌套阵列在某一时刻接收到K0(K0≤K)个信号源辐射的信号,这K0个信号源被称为这一时刻的活跃信号源,K0的数目未知,嵌套阵列接收的数据构成的最大似然估计函数的值由这K0个活跃信号源决定,与其他K-K0个缄默信号源无关。文献[24]推导了传统最大似然函数的上界满足:
(28)
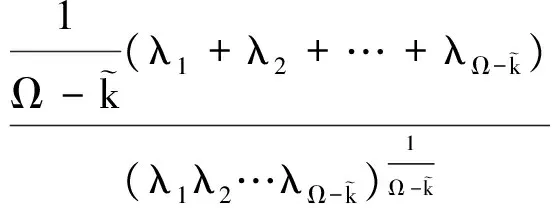
(29)
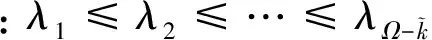
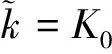
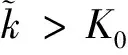
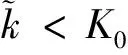
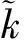
利用上文提出的嵌套阵列最大似然角度估计算法,估计出K个信号源的角度。这K个信号源的角度中只有K0个真实角度,其他均为虚假角度。根据最大似然估计的性质,真实角度对最大似然函数的值存在影响,虚假角度不影响最大似然函数的值,通过计算K个信号源角度分别对最大似然估计函数的影响度,影响度低的角度为虚假角度,这样能够找出K-K0个虚假角度。

(30)
空域中K个信号源信号都被嵌套阵列接收时,记为H0,除了θi之外,空域中其他K-1个信号源信号都被嵌套阵列接收时,记为Hi,利用对数似然比检验的方法进行判决:
(31)
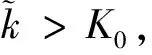
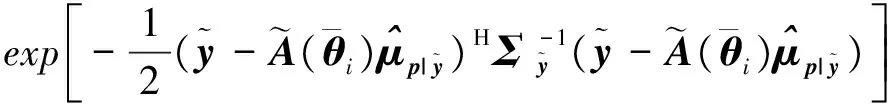
(32)
(33)
对数似然比R为
(34)
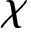
利用似然比与门限之间的关系,确定检测的角度是否为真实角度。通过多元假设检验的方法可以在前期最速下降法估计的K个角度中确定K0个活跃辐射源的真实角度。
5 仿真分析
假设存在由6个阵元组成的均匀线阵,阵元间距为d,分别用MUSIC算法和MLE算法对5个窄带辐射源方位进行估计,辐射源角度分别为:10°、30°、40°、60°和80°,在信噪比为0 dB,已知信源个数条件下,得到图2(a)和图2(b)。
假设存在6个阵元组成二级嵌套阵列,阵元间距分别为d、d、d、3d和3d,直接利用接收数据通过MUSIC算法和MLE算法对5个窄带辐射源方位进行估计,辐射源角度分别为:10°、30°、40°、60°和80°,在信噪比为0 dB,已知信源个数条件下,得到图2(c)和图2(d)。
从图2(a)和图2(b)中可以看出,当辐射源数目达到均匀线阵测向自由度时, MUSIC和MLE两种测向算法存在目标角度丢失、测向误差大的缺点。从图2(c)和图2(d)中可以看出,直接利用接收数据进行测向,MUSIC算法测向精度较高,但存在虚假角度;MLE算法无虚假角度出现,但是算法测向精度不高。通过前后的对比实验可知,嵌套阵列的布局方式增大了阵列孔径,但是常规的测向方法不能得到较好的测向结果。
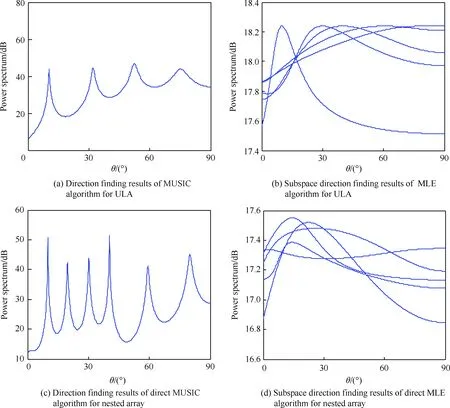
图2 两种阵列常规MUSIC和MLE算法测向结果Fig.2 Direction finding results of conventional MUSIC and MLE algorithms based on two arrays
已知信源个数条件下,利用第2部分的嵌套阵列信号处理模型,对二级嵌套阵列接收数据进行预处理之后,利用空间平滑MUSIC(Spatial Smoothing-MUSIC, SS-MUSIC)和MLE算法对10个辐射源进行测向,辐射源角度分别为-70°、-60°、-40°、-30°、-10°、10°、30°、40°、60°和70°。实验初始值采用等间隔初值,在-90°~90°等间隔取10个值。信噪比相同,仿真得到图3(a)和图3(b)。在存在4个相干辐射源条件下,其他条件不变,仿真得到图3(c)和图3(d)。
从图3(a)和图3(b)可以看出,通过本文第2节的信号模型处理之后,嵌套阵列具有扩大阵列孔径的效果,并且SS-MUSIC和MLE算法都有较高的测向精度和准确度。由于SS-MUSIC计算协方差时仅用到虚拟阵列一半的阵元,所以导致算法自由度损失了一半,而MLE算法利用的是全部虚拟阵元,因此自由度是前者的2倍。从图3(c)和图3(d)可以看出,和均匀阵列一样,在嵌套阵列测向中,MUSIC算法难以处理相干信号,而相干信号对MLE算法测向结果无影响。
在已知信源个数条件下,当不存在相干信号时,以6阵元二级嵌套阵为阵列模型,分别用SS-MUSIC和MLE算法在不同信噪比SNR和不同快拍数条件下,对K=10个信号,进行N=500次蒙特卡罗实验,利用式(35)计算均方误差,得到图4。
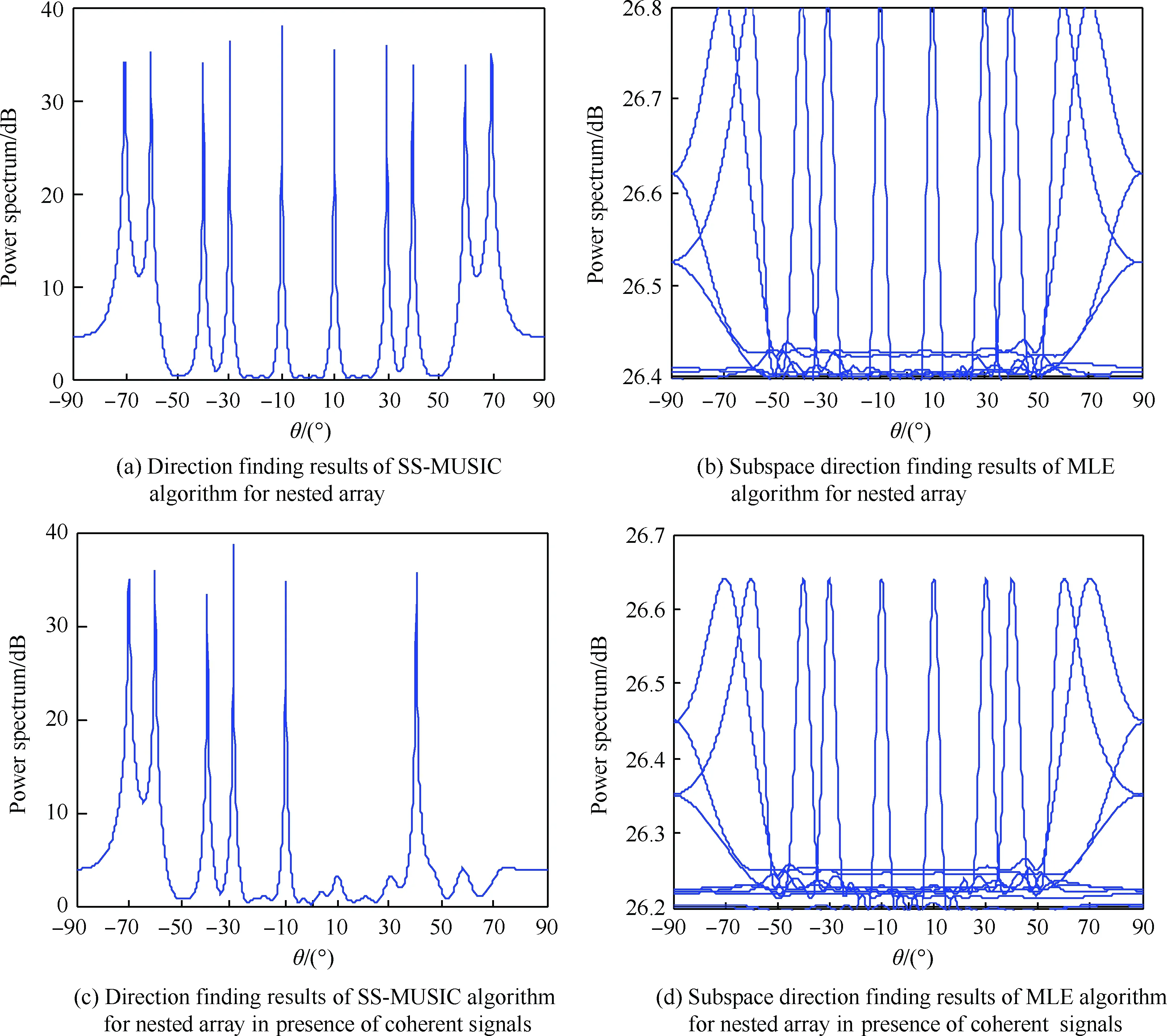
图3 数据预处理后嵌套阵列两种算法测向结果Fig.3 Direction finding results of two algorithms based on nested arrays after data preprocessing
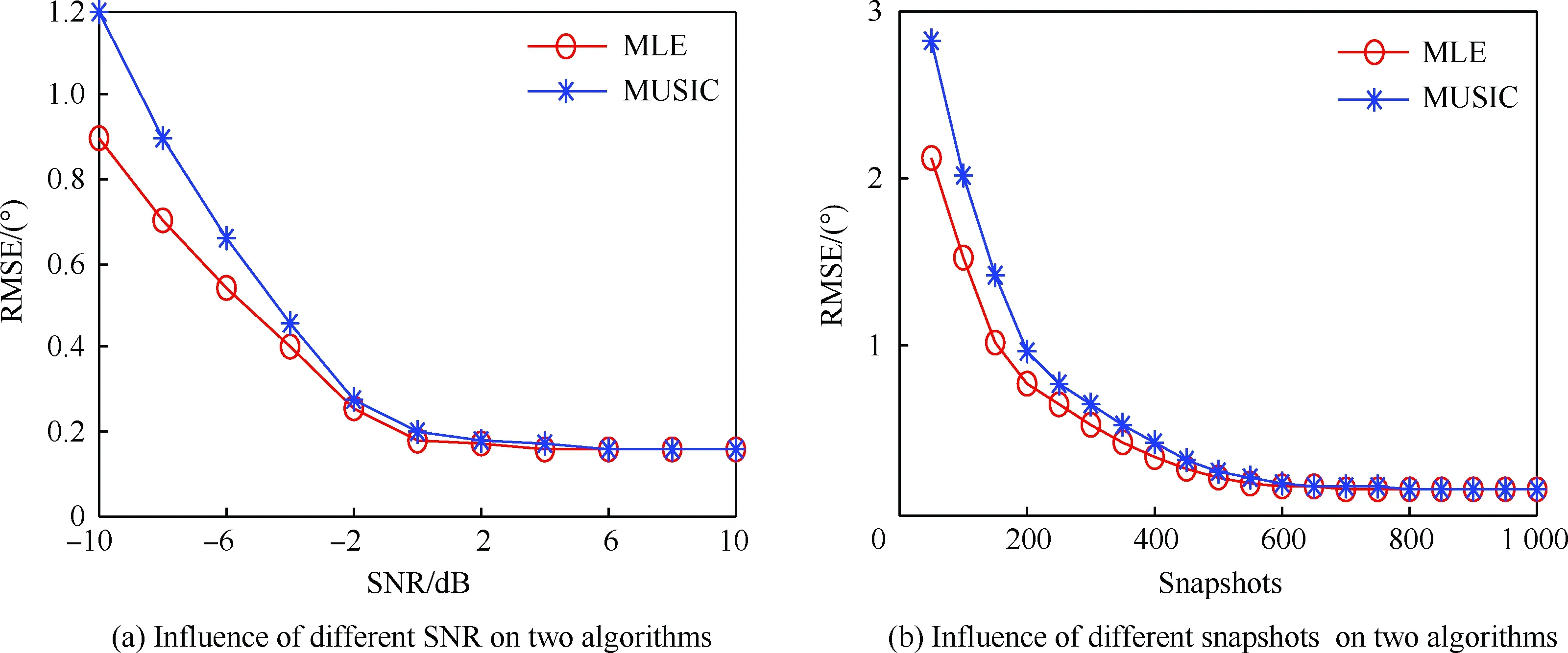
图4 两种算法测向性能比较Fig.4 Comparison of two algorithms for direction finding
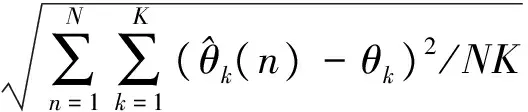
(35)
从图4(a)可以看出,当信噪比SNR>0 dB时,SS-MUSIC和MLE两种算法的测向精度基本相同,误差均小于0.2°,说明嵌套阵列下两种测向算法均具有较高的测向精度。当信噪比SNR<0 dB时,两种测向算法的角度估计精度有明显下降,但是MLE算法的测向精度要高于MUSIC算法,因为,MUSIC算法在信噪比较低时,会有部分噪声子空间泄漏到信号子空间,导致测向精度下降,所以MUSIC算法对噪声的敏感度要比MLE算法高。从图4(b)可以看出,当快拍数大于300时,MLE算法和MUSIC算法测向精度均较高,当快拍数小于300时,MLE算法的测向精度略高于MUSIC算法。
在辐射源个数未知的前提下,利用本文中的多元假设检验进行目标个数的估计。假设空域中共有10个潜在辐射源,角度分别为-70°、-60°、-40°、-30°、-10°、10°、30°、40°、60°和70°,在某一时刻发射信号的活跃辐射源为-10°、10°、40°和70°,利用本文中的多元假设检验的方法进行仿真,得到图5(a)和图5(b)。
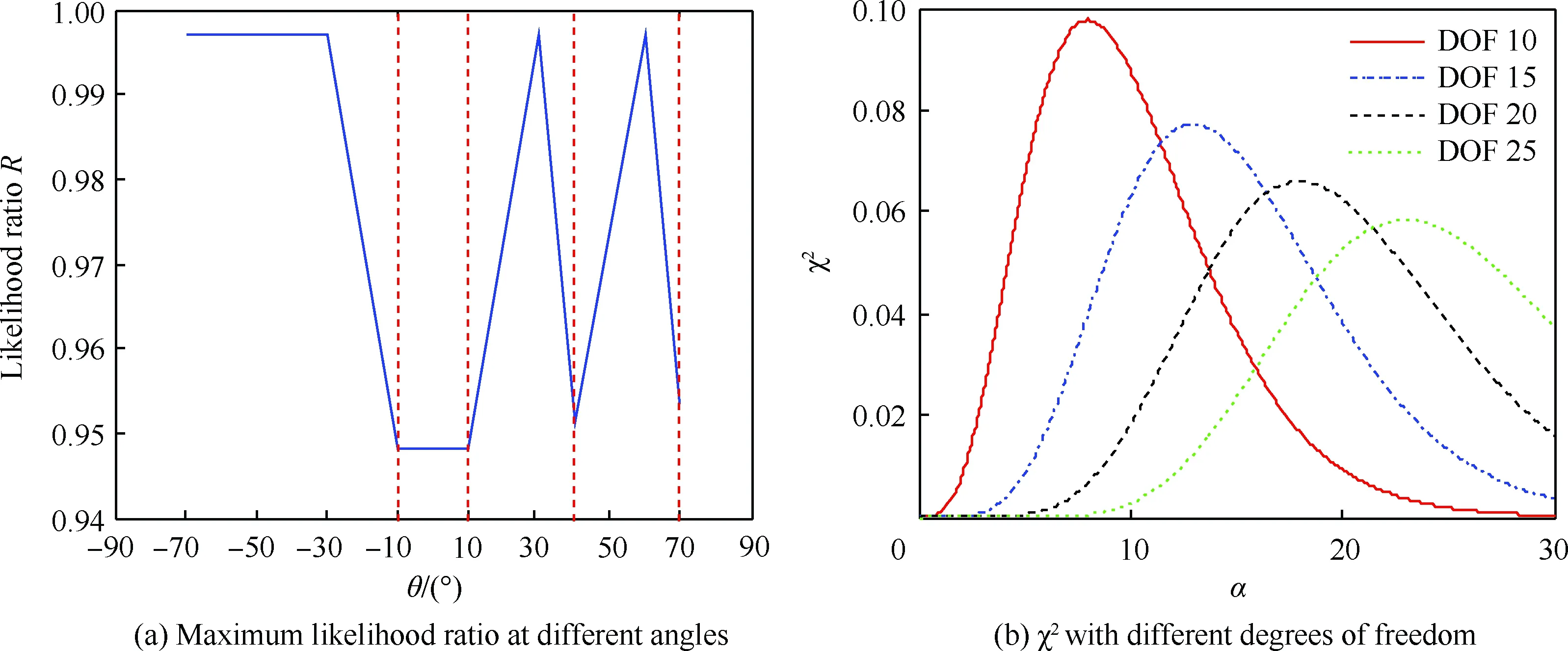
图5 多元假设检验Fig.5 Multiple hypothesis testing
对不同信源数目估计方法进行仿真分析。在不同信噪比条件下,存在5个角度分别为10°、30°、40°、60°和80°的信源,假设信源数目未知,分别采用本文提出的多元假设检验(Multiple Hypothesis Test, MUL TEST)、盖氏圆估计(Gerschgorin Disk Estimation, GDE)、最小描述长度(Minimum Description Length, MDL)准则和基于Akaike信息论准则(Akaike Information Criteria, AIC) 4种算法对信源数目进行估计,当不存在相干信号源时,得到图6(a),当存在相干信号源时,得到图6(b)。
图6(a)可以看出,在信噪比SNR<-15 dB条件下,前述的4种信源估计算法的估计正确概率均小于0.3,但是,多元假设检验估计方法正确率略高于其他3种算法。当信噪比-15 dB≤SNR≤-9 dB时,随着信噪比的增加,多元假设检验估计方法和MDL算法信源估计正确率均迅速提高,并且多元假设检验估计方法正确率高于后者,其他两种方法的正确率仍然小于0.3。当信噪比SNR>-9 dB时,随着信噪比的增加,多元假设检验估计方法和MDL算法信源估计正确率分别达到0.93和0.97,GDE算法和AIC算法迅速提高到0.97左右,并且随着信噪比不断增加,正确率不再继续提高。通过分析可知,在信噪比较低时,多元假设检验方法明显优于其他3种信源估计算法,在信噪比较高时,多元假设检验方法略逊于其他3种算法,但正确率仍达到了0.93以上。
图6(b)可以看出,在存在相干信源的条件下,GDE、MDL和AIC算法随着信噪比的增加,信源估计正确率均无提高,均小于0.2。由于多元假设检验采用最大似然估计的思想,因此信源估计正确率没有受到相干信源的影响,在信噪比SNR>-9 dB时,正确率仍然达到了0.93左右,说明在存在相干信源时,多元假设检验明显优于其他3种信源估计算法。

图6 4种信源数目估计算法比较Fig.6 Comparison of four algorithms for source number estimation
6 结 论
1) 本文提出了在辐射源个数未知的条件下嵌套阵列多辐射源角度估计算法,在嵌套阵列接收信号模型的基础上,推导了嵌套阵列多辐射源信号的最大似然函数及其梯度,利用最速下降法同时估计多个辐射源方位。
2) 针对辐射个数未知的问题,本文提出了基于最大似然比的多元假设检验信源数目估计算法,仿真实验表明,多元假设检验信源估计方法在低信噪比、相干信号处理算法方面均优于传统的3种信源估计算法。
3) 嵌套阵列极大提高了相同阵元数目条件下均匀阵列的测向自由度,嵌套阵列最大似然估计算法在低信噪比、低快拍数、相干信号处理方面均优于嵌套阵列MUSIC算法。
本文仅涉及窄带信号测向方面的问题,如何将算法推广到宽带信号测向方面是下一步研究的重点。
[1] LIU H Q, ZHAO L M, LI Y, et al. A sparse-based approach for DOA estimation and array calibration in uniform linear array[J]. IEEE Sensors Journal, 2016, 16(15): 6018-6027.
[2] LIAO B, WEN J, HUANG L, et al. Direction finding with partly calibrated uniform linear arrays in nonuniform noise[J]. IEEE Sensors Journal, 2016, 16(12):4882-4890.
[3] MOFFET A. Minimum-redundancy linear arrays[J]. IEEE Transactions on Antennas and Propagation, 1968,16(2): 172-175.
[4] ELIE B D, AHMAD F, MOENESS G A. Sparsity-based direction finding of coherent and uncorrelated targets using active nonuniform arrays[J]. IEEE Signal Processing Letters, 2015, 22(10): 1628-1632.
[5] BHARGAV A, GUPTA N. Multiobjective genetic optimization of nonuniform linear array with low sidelobes and beamwidth[J]. IEEE Antennas and Wireless Propagation Letters, 2013, 12(2): 1547-1549.
[6] MIKAEL S, LIEVEN D L. Multiple invariance ESPRIT for nonuniform linear arrays: A coupled canonical polyadic decomposition approach[J]. IEEE Transactions on Signal Processing, 2016, 64(14): 3693-3704.
[7] PILLAI S U, BARNESS Y, HABER F. A new approach to array geometry for improved spatial spectrum estimation[J]. Proceedings of the IEEE,1985, 73(10): 1522-1524.
[8] PILLAI S, HABER F. Statistical analysis of a high resolution spatial spectrum estimator utilizing an augmented covariance matrix[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1987, 35(11): 1517-1523.
[9] HBRAMOVICH Y I, GRAY D A, GOROKHOV A Y, et al. Positive-definite Toeplitz completion in DOA estimation for nonuniform linear antenna arrays. Ⅰ. Fully augmentable arrays[J]. IEEE Transactions on Signal Processing, 1998, 46(9): 2458-2471.
[10] HBRAMOVICH Y I, SPENCER N K, GOROKHOV A Y. Positive-definite Toeplitz completion in DOA estimation for nonuniform linear antenna arrays. Ⅱ. Partially augmentable arrays[J]. IEEE Transactions on Signal Processing, 1999, 47(6): 1502-1521.
[11] MA W K, HSIEH T H, CHI C Y. DOA estimation of quasi-stationary signals via Khatri-Rao subspace[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing. Piscataway, NJ: IEEE Computer Society, 2009: 2165-2168.
[12] PAL P, VAIDYANATHAN P P. Nested arrays: A novel approach to array processing with enhanced degrees of freedom [J]. IEEE Transactions on Signal Processing, 2010, 58(8): 4167-4181.
[13] MA X R, DONG X H, XIE Y F. An improved spatial differencing method for DOA estimation with the coexistence of uncorrelated and coherent signals[J]. IEEE Sensors Journal, 2016,16(10): 3719-3723.
[14] FANG W H, LEE Y C, CHEN Y T. Maximum likelihood 2-D DOA estimation via signal separation and importance sampling[J].IEEE Antennas and Wireless Propagation Letters, 2016, 15(2): 746-749.
[15] YANG X P, LI S, HU X N, et al. Improved MDL method for estimation of source number at subarray level[J]. Electronics Letters, 2016, 52(1): 85-86.
[16] HAN K Y, NEHORAI A. Improved source number detection and direction estimation with nested arrays and ULAs using jackknifing[J]. IEEE Transactions on Signal Processing, 2013, 61(23): 6118-6128.
[17] 齐崇英, 张永顺, 陈西宏, 等. 一种未知信源数的高分辨DOA估计算法[J].通信学报, 2006, 26(3): 58-63.
QI C Y, ZHANG Y S, CHEN X H, et al. Algorithm on high resolution DOA estimation under condition of unknown number of signal sources[J]. Journal on Communications,2006, 26(3): 58-63 (in Chinese).
[18] MANIKAS A N, TURNOR L F. Adaptive signal parameter estimation and classification technique[J].IEE Proceedings F-Radar and Signal Processing, 1991, 138(3):267-277.
[19] ZHANG Y, NG B P. MUSIC-Like DOA estimation without estimating the number of sources[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1668-1676.
[20] LIU C L, VAIDYANATHAN P P. Super nested arrays: Linear sparse arrays with reduced mutual coupling—Part Ⅰ: Fundamentals [J]. IEEE Transactions on Signal Processing, 2016, 64(15): 3997-4012.
[21] LIU C L, VAIDYANATHAN P P. Super nested arrays: Linear sparse arrays with reduced mutual coupling—Part Ⅱ: High-order extensions [J]. IEEE Transactions on Signal Processing, 2016, 65(16): 4203-4217.
[22] NIU C, ZHANG Y S, GUO J R. Interlaced double-precision 2-D angle estimation algorithm using L-shaped nested arrays[J]. IEEE Signal Processing Letters, 2016, 23(4): 522-526.
[23] HAN K Y, NEHORAI A. Wideband Gaussian source processing using a linear nested array[J]. IEEE Signal Processing Letters, 2013,20(11): 1110-1113.
[24] CHUNG P J. A max-search approach for DOA estimation with unknown number of signals[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(3): 612-619.
DOAestimationalgorithmbasedonmaximumlikelihoodestimationfornestedarray
CHENLu1,*,BIDaping1,2,CUIRui1,HANJiahui1
1.ElectronicEngineeringInstitute,Hefei230037,China2.KeyLaboratoryofElectronicRestriction,Hefei230037,China
Toestimatetheanglesofmultipleradiationsourceswithunknownnumbersofsignals,thispaperpresentsanalgorithmforangleestimationofthenestedarraybasedonMaximumLikelihoodEstimation(MLE).Basedonthenestedarraymodel,themaximumlikelihoodfunctionanditsgradientofthemultiplesignalsinterceptedbythenestedarrayarederived.Theanglesofallradiationsourcesintheairspaceareestimatedbythesteepestdescentmethod.Usingthemethodofmultiplehypothesistesting,themaximumlikelihoodratioandthethresholdarecomparedtodeterminetheactiveradiationsourceangleofthetransmittedsignalatacertaintimeandexcludefalsesourceangles.TheproblemofDOAestimationofmultipleradiationsourceswithunknownnumberofsignalsbythenestedarrayisthussolved.Thesimulationresultsshowthatundertheconditionsofunknownnumberoftheradiationsource,existingcoherentsignal,lowSignaltoNoiseRatio(SNR),andlowsamplingnumber,theproposedalgorithmhasbetterperformanceinangleestimationthantraditionalMUltipleSIgnalClassification(MUSIC)algorithm.ThemethodofmultiplehypothesistestinghasmoreadvantagesthantraditionalsourcenumberestimationalgorithmsundertheconditionoflowSNRandintheprocessingofcoherentsignals.
nestedarray;MaximumLikelihoodEstimation(MLE);angleestimation;multiplehypothesistesting;numberofsignals
2017-03-02;Revised2017-05-15;Accepted2017-06-22;Publishedonline2017-06-291322
URL:http://hkxb.buaa.edu.cn/CN/html/20171125.html
s:NationalNaturalScienceFoundationofChina(61671453);NaturalScienceFoundationofAnhuiProvince(1608085MF123)
.E-mailchenluzhanjing@126.com
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2017.321212
V219;TN971.1
A
1000-6893(2017)11-321212-12
2017-03-02;退修日期2017-05-15;录用日期2017-06-22;< class="emphasis_bold">网络出版时间
时间:2017-06-291322
http: //hkxb.buaa.edu.cn/CN/html/20171125.html
国家自然科学基金(61671453);安徽省自然科学基金 (1608085MF123)
.E-mailchenluzhanjing@126.com
陈璐,毕大平,崔瑞,等.嵌套阵列最大似然估计测向算法J. 航空学报,2017,38(11):321212.CHENL,BIDP,CUIR,etal.DOAestimationalgorithmbasedonmaximumlikelihoodestimationfornestedarrayJ.ActaAeronauticaetAstronauticaSinica,2017,38(11):321212.
(责任编辑:苏磊)
附录A
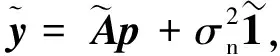


(A1)
忽略常数项得
(A2)
展开去掉常数项可得
(A3)
其中:
(A4)
(A5)
附录B
(B1)

(B2)
(B3)
(B4)
求P(1)关于θ的导数时,将g视为常数。则
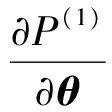
(B5)
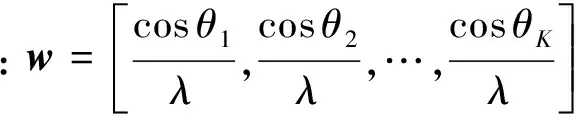

(B6)
求P(2)关于θ的导数时,将z视为常数。则

(B7)
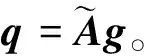
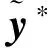
(B8)
进一步合并可得
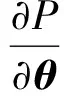

(B9)
则
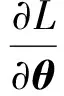
(B10)

