高超声速进气道低马赫数不起动和再起动试验

王晨曦，谭慧俊，*，张启帆，孙姝

1.南京航空航天大学 能源与动力学院 江苏省航空动力系统重点实验室，南京 210016 2.南京航空航天大学 民航学院，南京 210016

高超声速进气道低马赫数不起动和再起动试验

王晨曦1，谭慧俊1，*，张启帆1，孙姝2

1.南京航空航天大学 能源与动力学院 江苏省航空动力系统重点实验室，南京 210016 2.南京航空航天大学 民航学院，南京 210016

为拓展对高超声速进气道不起动机理的认识，对一截短的二元高超声速进气道的低马赫数不起动现象和再起动现象进行了风洞试验研究。试验中分别通过改变进气道攻角和在通道下游设置堵锥形成流动壅塞的方法来模拟进气道来流马赫数的改变和燃烧室内释热导致的流动壅塞。试验中采用高速纹影技术和动态压力测量技术对上述动态过程中的瞬态流动结构和壁面动态压力信号特征进行了记录。研究发现，当进气道处于低马赫数不起动时，其口部分离包诱导激波受分离包自身振荡特性的影响，在唇口附近连续的小幅振荡，进而给整个进气道通道内引入了一类无基频的小幅压力扰动。而该扰动随着马赫数的增加，进气道恢复起动后逐渐消失。此外，还捕捉到了进气道再起动过程中分离包吞入的迟滞现象，进气道从“小喘”阶段恢复至起动状态时，由于下游高压的存在使得分离包未能完全吞回，并出现了类似低马赫数不起动时的无基频小幅振荡。该振荡直至通道下游完全敞开、口部分离包被吞入才逐渐消失，至此进气道也顺利地恢复到了起动状态。

高超声速进气道；低马赫数;不起动；再起动；迟滞

作为吸气式高超声速推进系统的关键气动部件以及机体/推进系统一体化的重要因素，高超声速进气道(简称高超进气道，下同)的设计形式和工作特性直接影响着推进系统整体效能的发挥，为此一直以来有大量的研究工作致力于各类高超进气道的设计方法与性能改善。

一般，当进气道的捕获特性未因内部流态的变化而受到影响时，称进气道处于起动状态，否则为不起动状态[1]。可见不起动作为高超声速进气道中的一种典型非正常工作状态，一旦进气道进入到该状态，其流场品质急剧恶化，并伴随着总压恢复系数和流量系数的骤降。随之带来的剧烈的波系运动和壁面压强振荡，不仅会使发动机的推力特性严重恶化甚至熄火，还加大了对飞行器的控制难度[2]。纵观近年来国际上一系列高超声速飞行计划，如1998年美国航空航天局与俄罗斯中央航空发动机研究院联合进行的超燃冲压发动机试验[3]、2007年美国DARPA(Defense Advanced Research Projects Agency)与澳大利亚Queensland大学联合进行的飞行试验[4]以及2011年6月美国空军进行的X-51A高超声速飞行器第二次飞行试验[5]中,均是由于出现了进气道不起动现象，进而直接导致了飞行试验的失败或者未达到预期的目标。为此，有必要对其开展针对性的研究工作。

自Oswatitsch[6]于1944年首次观测到超声速进气道的振荡流态(即喘振)以来，已有大量关于进气道不起动流态方面的研究[7-15]。近年来，得益于高速纹影摄像和瞬态压强测试技术的发展，Tan[16-17]、Wagner[18-19]和Li[20]等针对广义的高超进气道模型对其下游堵塞导致的不起动动态过程进行了细致的刻画。研究结果表明，高超声速进气道的不起动流态极易表现为振荡流态，且可分为相对温和的“小喘”和剧烈的“大喘”2种。除上述2种典型的振荡类型之外，Chang等[21]还在其高超进气道不起动试验中观察到了两种新奇的振荡类型：一种是混合了“小喘”和“大喘”的振荡形式，另一种是间歇振荡形式。此外Zhang等[22]还发现在典型的“大喘”振荡形式中还耦合着高频低振幅的二次谐振，且该谐振的产生和声学振荡息息相关。之后，Jiao[23]和Zhang[24]等在对工作在超额定工况下高超进气道的不起动流场研究中，发现了一种表现为进口前脱体弓形波小幅振荡的“局部不起动”现象。

可以看到目前关于高超声速进气道不起动的研究工作仍主要是集中在流场振荡相对剧烈的下游流动壅塞导致的不起动现象，然而对于流场振荡相对温和的喉道发生流动壅塞的不起动现象以及进气道再起动过程中的非定常特性却鲜有相关的试验研究。鉴于上述两种现象的流场结构变化相对较小，因此近年来的研究还是停留在仿真[25-27]和定常的测量手段[28-29]上，而这显然不能够完全揭示其中的现象和流动机理。对此，本文结合一截短的高超声速进气道模型，针对其在低马赫不起动和再起动过程中出现的非定常流动现象开展了风洞试验研究，并对其中的流动机理进行了分析。

1 研究对象

为配合现有的风洞条件(最大风洞马赫数为3.8)，并尽可能真实地模拟高超声速进气道中的流动，在设计相应的进气道模型时，假设该进气道的上游还存在一级压缩面为10°折转角的虚拟压缩面，经过该压缩面后，可使高超声速来流减速至风洞马赫数范围内，因此该实验模型实际上为将一级压缩面截短后的高超声速进气道(图1)。该进气道设计在风洞来流马赫数3.8状态下封口，二级压缩面和唇罩处的气流折转角分别为10°和8°，进气道的内收缩比为1.53。喉道口后紧接的等截面隔离段通道高为15 mm、宽为40 mm，且和风洞自由流方向的夹角为10°，以匹配虚拟一级压缩面的气流偏折。在模型内流道的两侧安装有两块光学玻璃以进行流场显示，其可视区域为110 mm×15 mm，在高度方向覆盖了整个内通道。此外，为了获得瞬态的壁面压强信息，在进气道模型的前体压缩面(测点R1-R9)和内通道上下壁面(测点C1-C13和测点D1-D7)上共布置了29个动态压力传感器，具体如图1所示。然而若干个传感器在试验过程中出现了损坏，损坏的测点在图中使用空心黑框进行了标注，并在随后的压力数据处理中被剔除。

另外，在流道的出口设置了二元楔形堵块来模拟燃烧可能导致的流动堵塞。楔形堵块的全顶角为40°，其尖点位于燃烧室流道的半高处，可在步进电机的控制下沿流向移动，以在流道出口附近形成可控的流动壅塞。出口堵塞度TR定义为

TR=(1-Ath,plug/Acombustor)×100%

(1)

式中：Ath,plug为堵块附近形成的喉道面积;Acombustor为燃烧室横面积。

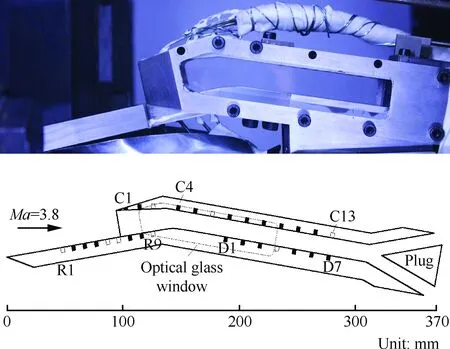
图1 风洞试验模型Fig.1 Wind tunnel test model

2 试验条件及测试手段

本文中的风洞验证试验在南京航空航天大学的超声速流动机理试验台进行。该试验台为一自由射流式超声速风洞，其主要由过渡段、稳定段、喷管段、试验舱以及下游真空罐组成。风洞采用真空抽吸式运行，上游为环境大气，下游与真空罐相连通，运行过程中，试验台将环境空气直接吸入，并通过喷管加速至超声速，在经过试验段后通过扩压器收集，最后进入真空罐内。通过下游真空罐的抽吸，可以保证风洞连续运行的时间t>20 s。风洞通过其上游较大口径的过渡段直接从大气中收集气体，不仅避免了下吹式风洞所需的复杂供气系统，而且使来流的均匀性更好，提高了风洞流场的品质。风洞喷管出口尺寸为200 mm×200 mm，试验舱的两侧壁安装有厚度20 mm的光学玻璃作为光学观察窗，尺寸为280 mm×205 mm，以便对试验舱内试验模型的流场进行光学观测。由于单个喷管只能满足特定马赫数的试验需求，为此风洞喷管设计为可更换部件，并设计和加工了多个典型马赫数(最高为Ma=3.8)的喷管。依据本文的研究目标，对应的研究工作主要在相对较低的马赫数Ma=3.0下开展，表1给出了此时风洞相应的来流参数。

试验中通过在模型上安置动态压力传感器对压力进行实时记录。传感器固有频率为50 kHz，压力传感器感转换出来的电信号采用NI公司的6255采集卡进行采集，其采样时间覆盖了风洞的整个工作过程，单通道采样率为20 kB/s。另外，采用瑞士IDT公司的MotionPro Y5高速摄影仪对模型的进口段及内流道流态进行了观察，本试验中的拍摄频率设置为1 500帧/s。为了满足高速拍摄时摄影仪对进光量的需求，试验中专门定制了高亮度的LED灯作为光源，并配备了400 mm f/5.6镜头 (Nikon Nikkor)进行拍摄。在试验过程中，当风洞流场完全建立后，利用外部脉冲信号触发高速摄影仪，该触发信号同时还被数据采集系统记录，以实现压力测量与纹影摄像间的同步。

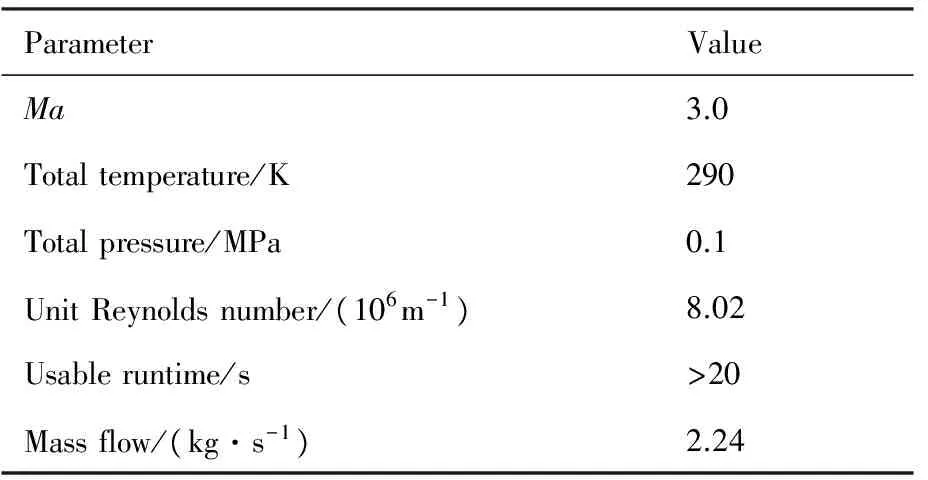
表1 超声速风洞试验的试验条件Table 1 Test conditions of supersonic wind tunnel test

3 不起动过程

为了探究该进气道在低来流马赫数下的进气道不起动特性，本文拟通过调节模型的攻角α达到改变进气道进口马赫数的目的，从而模拟实际情况下来流马赫数的变化。对此本文在来流马赫数Ma=3.0状态下选择了3个攻角，其具体的攻角状态和进气道进口马赫数如表2所示。试验中为了排除来自通道下游的影响，试验过程中下游堵锥将一直被设定在完全放开的状态(TR=0%)。

依照表2中进口前马赫数由低到高的排布规律，本文首先选取了0°攻角下对应进口马赫数Ma=2.5的状态进行分析。图2给出了该状态下进气道随风洞起动时的流场纹影照片，可以看到此刻即使进气道下游堵锥已完全放开，进口前仍存在一较大的分离包。与此同时，该分离包的诱导激波已完全跨过进气道唇罩，产生了一定程度的溢流，也就是说此时的进气道处于不起动状态。鉴于下游已完全放开，且口部存在巨大的分离包堵塞了通道，因此可将此时的不起动现象归为喉道壅塞导致的不起动。结合试验测得的纹影数据来看，该状态下的低马赫数不起动流场并非稳态定常的，其内部充斥着一定强度的非定常性。为此，在图3中分别给出了试验中口部分离包分别处于最大和最小状态的流场结构，可以看到分离包诱导激波在进气道唇口附近不停地摆动。

针对上述振荡流场，接下来继续结合瞬态压力数据对其进行进一步的分析。鉴于其不起动流场结构的非定常性，本文选取了一段长1 s的压力样本区间，旨在排除瞬态效应的影响，并从中计算得到了进气道壁面静压p的时均值paver(图3(a))和脉动均方根值prms(图3(b))沿程分布曲线。压力数据均采用来流静压p0进行无量纲化处理。可以看到， 由于进口部分离包在不断地涨大和缩小， 而越靠近进口的测点受分离区内高压的影响越大，因此前体压缩面测点的压力脉动值

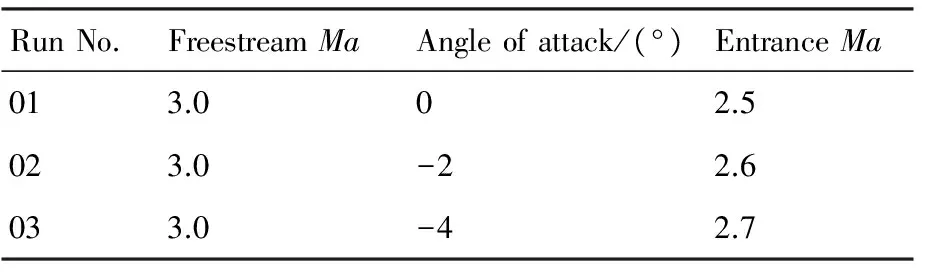
表2 低马赫不起动研究车次状态Table 2 Run list in low Mach number unstart process

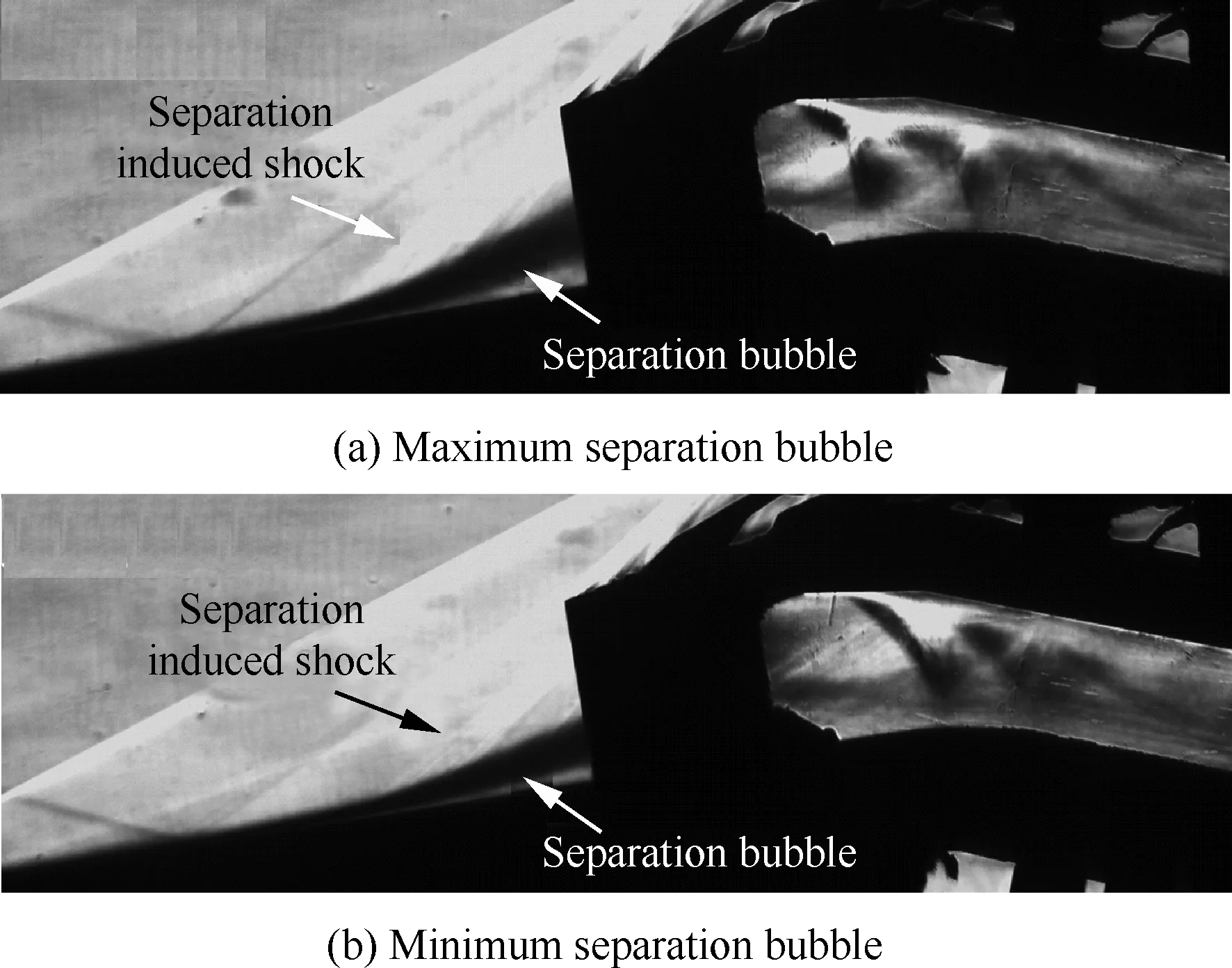
图2 0°攻角下进气道通流不起动流场结构Fig.2 Unstart flow pattern of inlet flow passage at α=0°

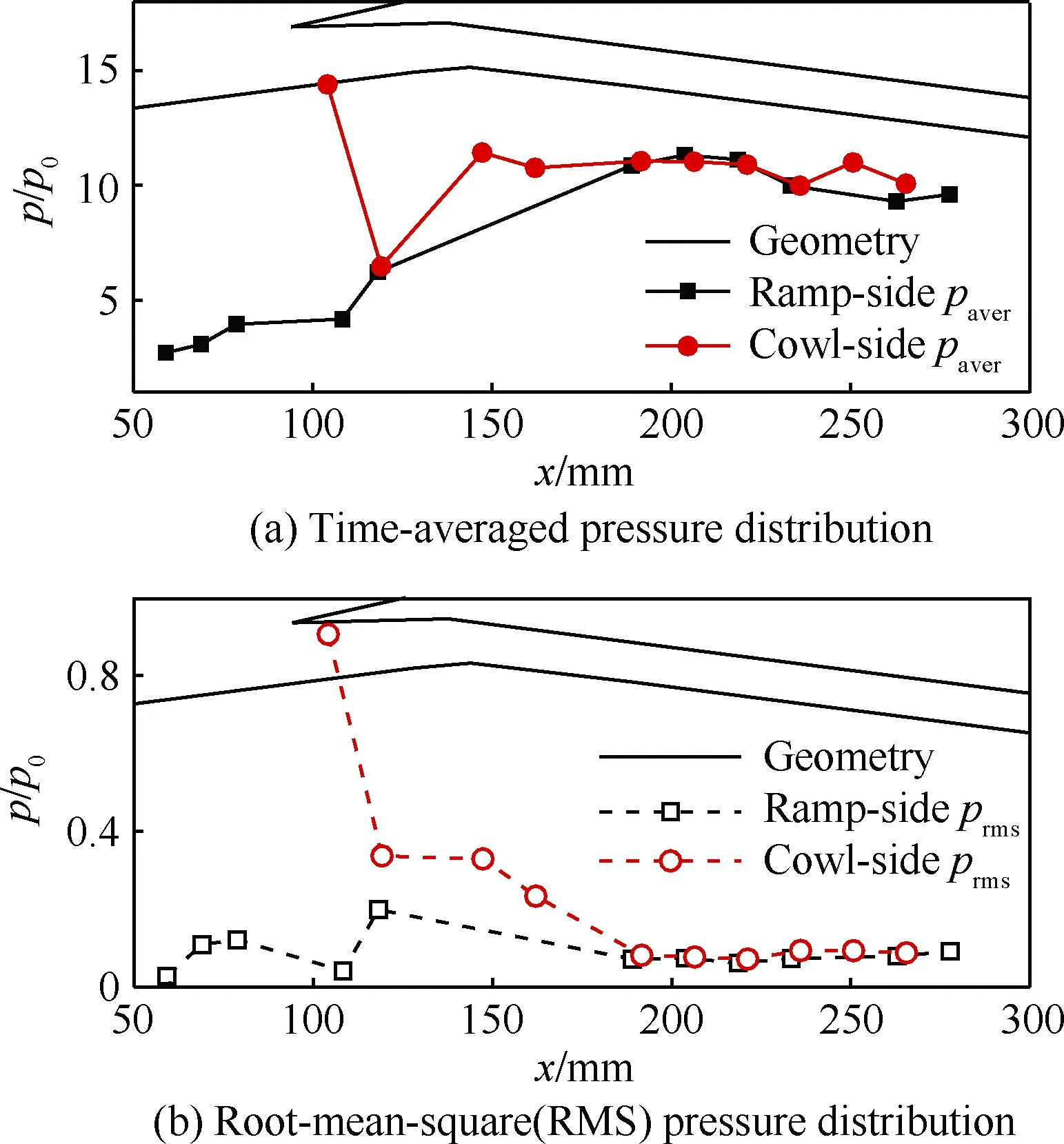
图3 0°攻角下进气道通流不起动阶段沿程静压分布Fig.3 Distribution of static pressure of unstarted inlet flow passage at α=0°

不断增大，同样也伴随着时均压力的增大。而到了进气道进口段，在通道内唇罩激波、反射激波的作用下，压缩面侧的压力时均值依旧持续上升，而其压力脉动值受激波入射位置影响较大，因此呈现出小幅的波浪式起伏。于此同时，在另一侧的唇罩，最上游的C1测点由于受到分离诱导激波的连续扫掠，其时均值(14.2p0)和脉动值(0.9p0)均为极大值，而紧接其后的C2测点则是在分离包后膨胀扇的作用下压力大幅下降。在此之后的通道内时均压力依旧不断升高，最后稳定在10p0左右，并且通道内上下壁面的压力非常接近，这也就是说此时通道后半段内的流速已相对较低，通道内无明显的波系结构。而另一方面，通道内下游测点由于远离了作为扰动源的分离包，且下游并无堵锥的干扰，其压力脉动均方根值也将不断减小，最后趋于稳定在0.09p0附近。

由上文的分析可知，该进气道在0°攻角下未能起动，且表现出了一定幅度的振荡。为了获得该流场的振荡特性，图4给出了整个流程中压力脉动最大的C1测点压力功率谱密度(Power Spectral Density,PSD) 分布，以表征整个流场的振荡特性,f为频率。可以看到C1测点压力信号中并未出现稳定的周期性振荡和振荡基频，其振荡能量主要集中在400 Hz以下。而该振荡频率较接近无穷远下游反馈影响下的分离流振荡频率[30]，即该扰动主要是来自于分离包自身的非定常性。且通道下游敞开，缺乏形成稳定振荡反馈的声速截面，因此该分离包的压力扰动并未在下游得到放大和反馈，进而也未出现稳定的振荡基频。

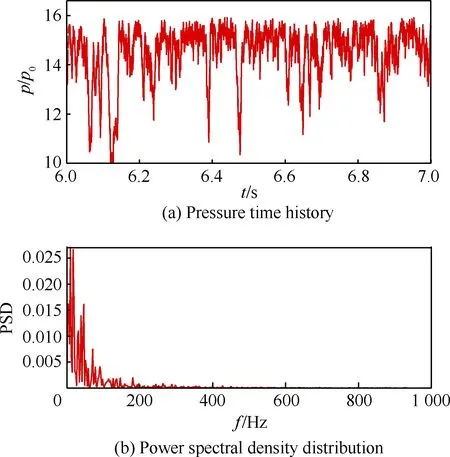
图4 0°攻角下进气道通流不起动阶段 C1测点压力信号Fig.4 Pressure signals of C1 point in unstarted inlet flow passage at α=0°

图5 -2°攻角下进气道通流不起动流场结构Fig.5 Unstart flow pattern of inlet flow passage at α=-2°

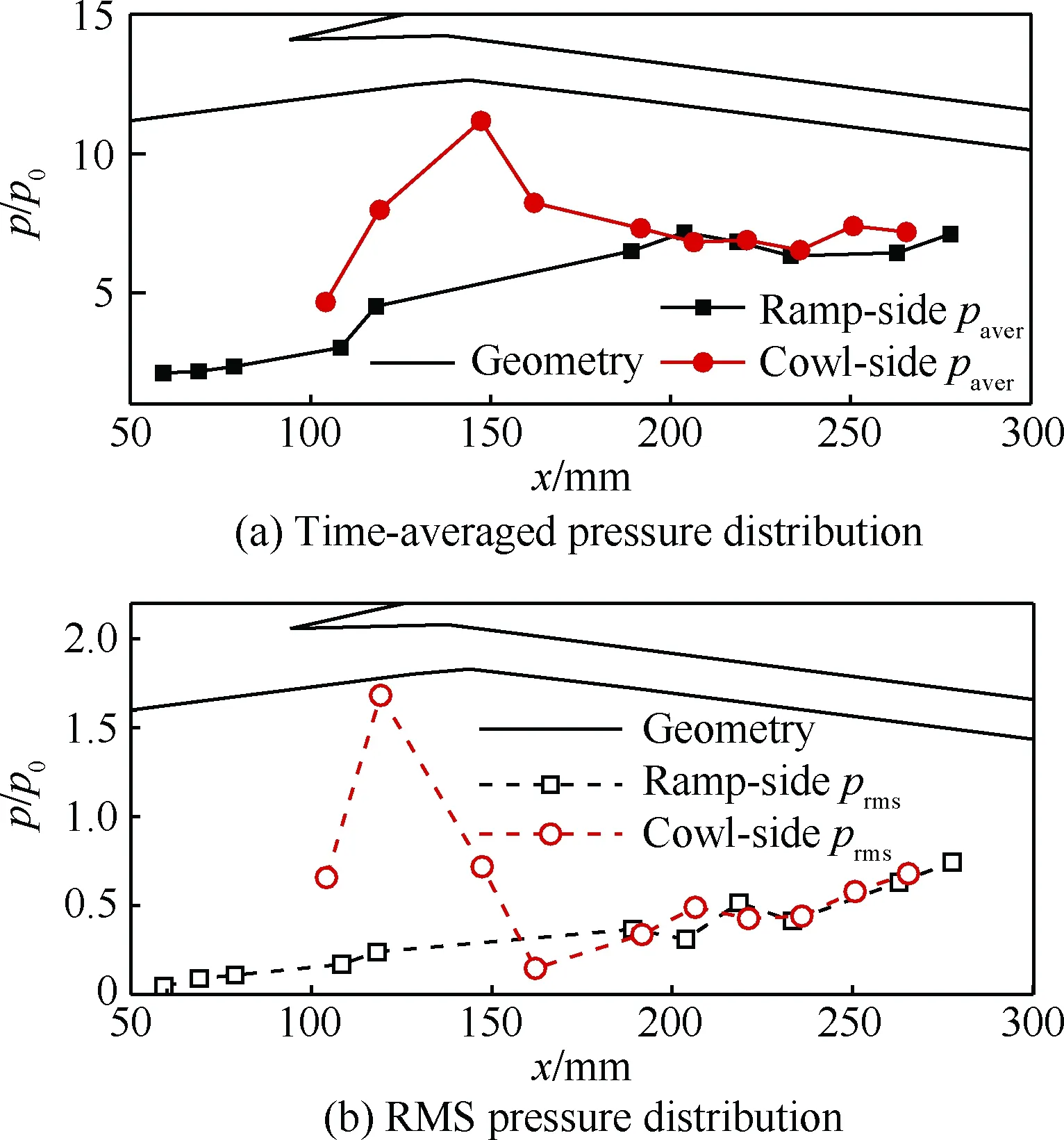
图6 -2°攻角下进气道通流不起动阶段静压分布Fig.6 Distribution of static pressure of unstarted inlet flow passage at α=-2°

接下来通过减小进气道攻角，以获得进口马赫数的增大对进气道流场结构的影响规律。图5首先给出的是-2°攻角下进气道随风洞起动的流场结构，虽然口部分离包依旧存在较大幅度的振荡，但是其在形态上较0°攻角状态已大幅减小。并且当分离包处于最大状态时，其分离诱导激波才刚跨过唇罩。而当分离包处于最小状态时，其已完全退回到进口段内，对应的分离诱导激波强度也大大减弱。也就是说在该状态的大部分时间内，该进气道仍是处于起动状态的。同样的，在图6中给出了此时进气道的沿程压力的时均值和脉动均方根值的分布。时均值分布上，压缩面侧测点的压力变化趋势和0°攻角的非常相似，均呈现出一种连续上升的趋势。唇罩侧的压力由于受分离包诱导斜激波后移的影响，唇罩压力的极大值点也逐渐向下游移动，在这之后的通道下游，上下壁面压力的时均值逐渐靠近，并趋于稳定。另一方面，在脉动均方根值分布上，和前文的试验结果也非常相似，由于受到分离包诱导激波不停扫掠的影响，其进口段唇罩侧测点压力的均方根值要远大于压缩面的和通道内的。除此之外，其极大值点也由之前的C1测点后移至C2测点。图7给出了脉动最剧烈的C2测点压力功率谱密度分布，类似于图4，并未出现明显的振荡基频。

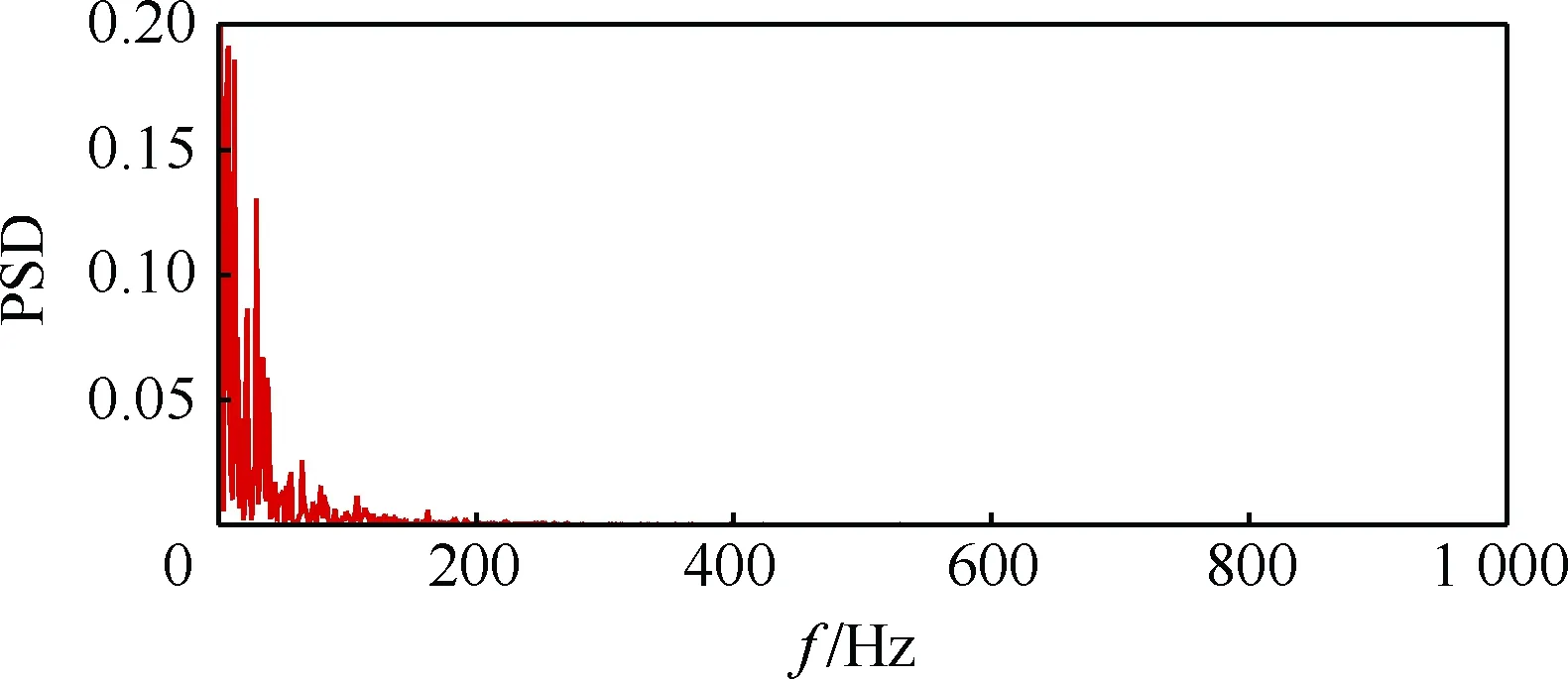
图7 -2°攻角下进气道通流不起动阶段C2测点 压力功率谱密度分布Fig.7 Distribution of power spectral density of C2 point in unstarted inlet flow passage at α=-2°

图8 -4°攻角下进气道通流起动流场结构Fig.8 Start flow pattern of inlet flow passage at α=-4°

在上文攻角状态的基础上，继续减小攻角至-4°，进口马赫数增加至Ma=2.7。在进气道流场建立之初，在进口段依旧存在一个分离包(图8)，占据了通道约1/3的高度。但是该分离包并未出现类似上文的大幅振荡，且其分离包诱导激波并未跨过唇罩，也就是说此时进气道处于起动状态。另一方面，通道的沿程压力在时均值(图9)和脉动均方根值(图10)分布规律上和前述2个状态相类似，但是其通道后半段上下壁面的时均压力开始交替出现波动，这表明通道内开始出现较强的激波反射现象了。此外，由于分离包振荡幅度的大幅减小，因此通道内的压力脉动均方根值相较上文2个状态也整体大幅降低。

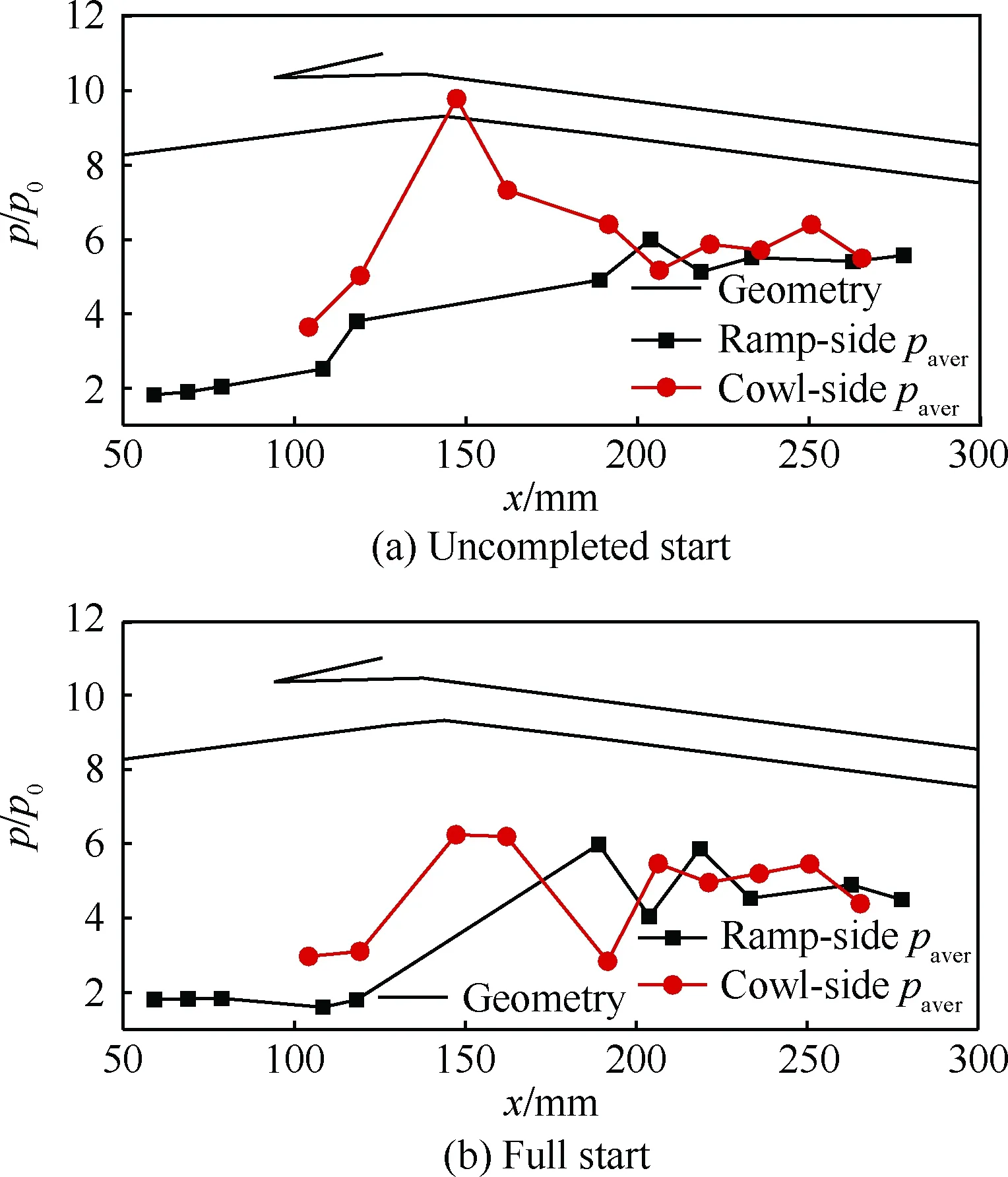
图9 -4°攻角下进气道通流起动阶段静压时均值分布Fig.9 Distribution of time-averaged static pressure of started inlet flow passage at α=-4°

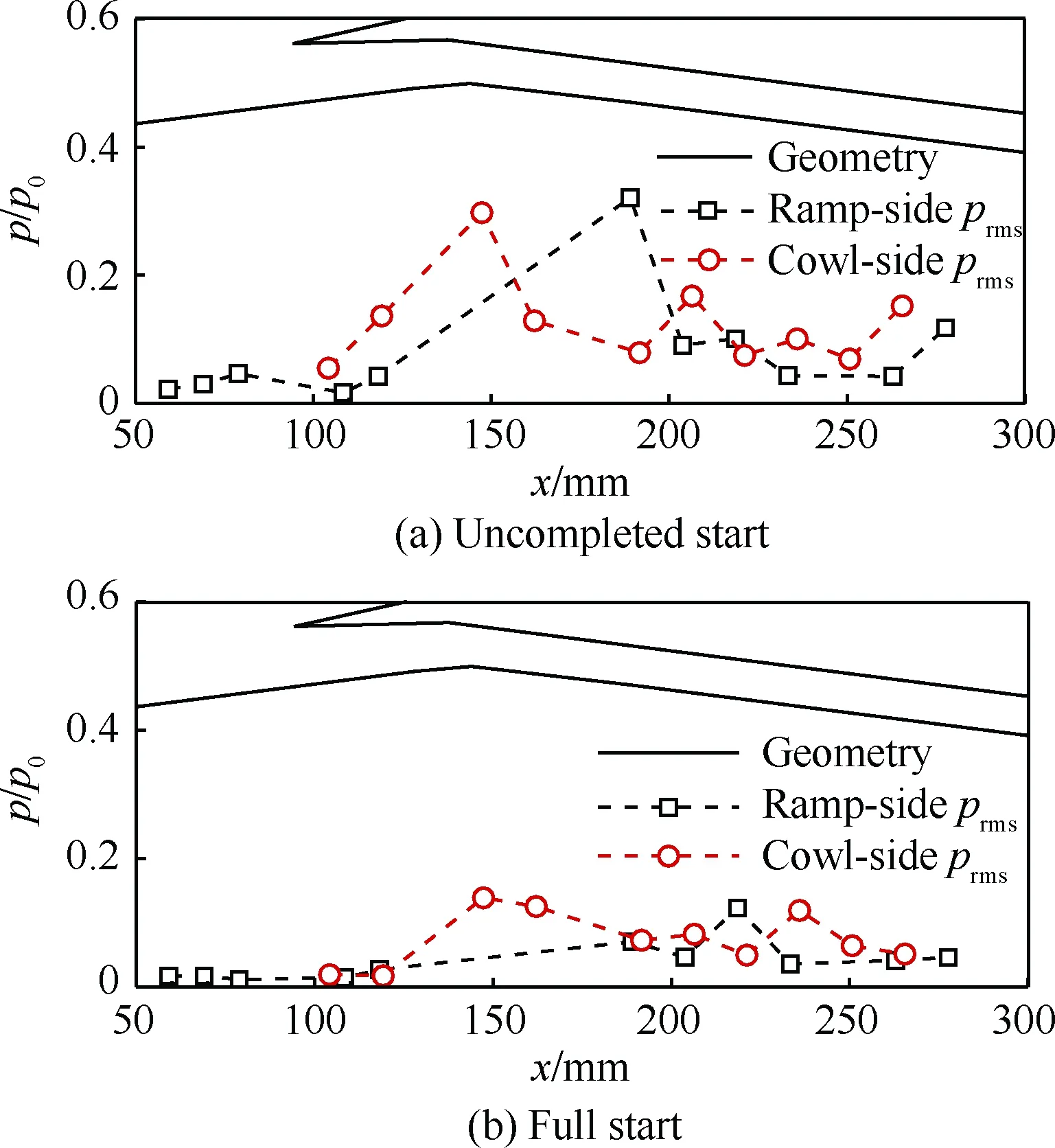
图10 -4°攻角下进气道通流起动阶段静压脉动 均方根值分布Fig.10 RMS static pressure distribution of started inlet flow passage at α=-4°

然而在试验中发现，图8(a)所示的口部分离包状态并不是稳定的状态，在随后的稳定吹风过程中，分离包将突然被完全吞入通道内(图8(b))。为了区分2个状态，本文称留有分离包的状态为未完全起动状态，分离包被吞入为完全起动状态。由于没有了分离包及其诱导激波的影响，其上唇罩侧的压力时均值大幅降低，而上进口段测点的压力脉动均方根值也是随之同步降低。对于该现象，本文认为此时的进气道恰好处于非常敏感的临界起动状态，因此初始进气道随风洞起动时在进口处产生了较大的分离包。但是该流场并不是稳定的，在受到扰动后，该分离包将被完全吞入通道内，至此进气道就实现了完全起动。

4 再起动过程

由上文的分析可知，该进气道在-4°攻角下就已实现了起动，但是其流场结构并不稳定。对此，本文接下来将继续减小攻角至-6°(进口马赫数Ma=2.8)，在保证进气道能正常起动的同时，通过对尾锥电机的控制获得了进气道从起动到不起动再起动的全过程，并检验了该进气道在此状态下的再起动能力。首先给出的是进气道通流流场结构(图11)，此刻进气道捕获波系正常建立，进气道处于起动状态，且在进口段未再出现大范围的分离，进口处产生的激波和膨胀扇交替反射并向下游传去。

试验中，通过控制电机台阶式进锥+退锥组合的控制方式获得了该进气道从起动到不起动，最后再起动的全动态过程。这其中进锥和退锥的次数均为10次(锥位01-10为进锥，锥位10-19为退锥)，为了增强进/退锥的可对比性，进锥和退锥的行程为一一对应的，表3中列出了进退锥过程中各锥位所对应的堵塞度TR值。

图11 -6°攻角下进气道通流起动流场结构Fig.11 Start flow pattern of inlet flow passage at α=-6°

接下来将进一步地对该再起动过程进行深入的分析，为了获得对整个动态过程最直观的认识，图12中给出了整个进锥和退锥过程中的最下游D7测点的压力时间曲线。可以看到整个压力历程大体上以锥位10为对称轴，呈对称分布。但是在进气道刚进入不起动状态(02-03锥位)和回到起动状态前的(17-18锥位)压力信号特性存在较大差异，存在一定的迟滞。对此，接下来将逐步展开详细的对比和分析。

由图12可以看到在锥位02下游压力仍未传至D7测点，在随后的锥位03(TR=20.2%)出现了明显的压力振荡，但是其振荡幅值却远低于后续锥位的压力振荡幅值，该种类型的振荡往往被称为“小喘”状态。图13中详细给出了该锥位平台下的最下游测点压力信号时间历程和其功率谱密度分布。可以看到，虽然该状态下的压力振荡幅度并不稳定，但是其压力信号的功率谱密度分布中已出现了明显的能量集中，即振荡基频。

结合纹影结果，图14中给出了在该“小喘”阶段口部分离包依次处于最大和最小状态时刻的流场结构。可以看到，即使是在口部分离包处于最小的状态时，其分离诱导激波依然位于进口前，并未被吞入通道内。整个“小喘”过程表现为口部分离诱导激波在进气道口外的小幅振荡。而通道内的流场结构较第3节中的流场结构显得更加复杂，且振荡幅度也更大。对此，图15中也同样给出了压力时均值和脉动均方根值的沿程分布曲线。对比上文的低马赫数不起动状态的结果(图3)发现，两者的压力时均值分布规律非常相似，但是脉动值在通道内的变化规律却存在较大的差别。低马赫数不起动状态下的通道压力脉动值沿程基本保持不变，但是在“小喘”状态下却呈现出沿流向不断增大的趋势。这是由于下游堵锥的前移在通道下游形成了流动壅塞，因此由上游分离包产生的扰动在往下游传播的过程中得到了放大。

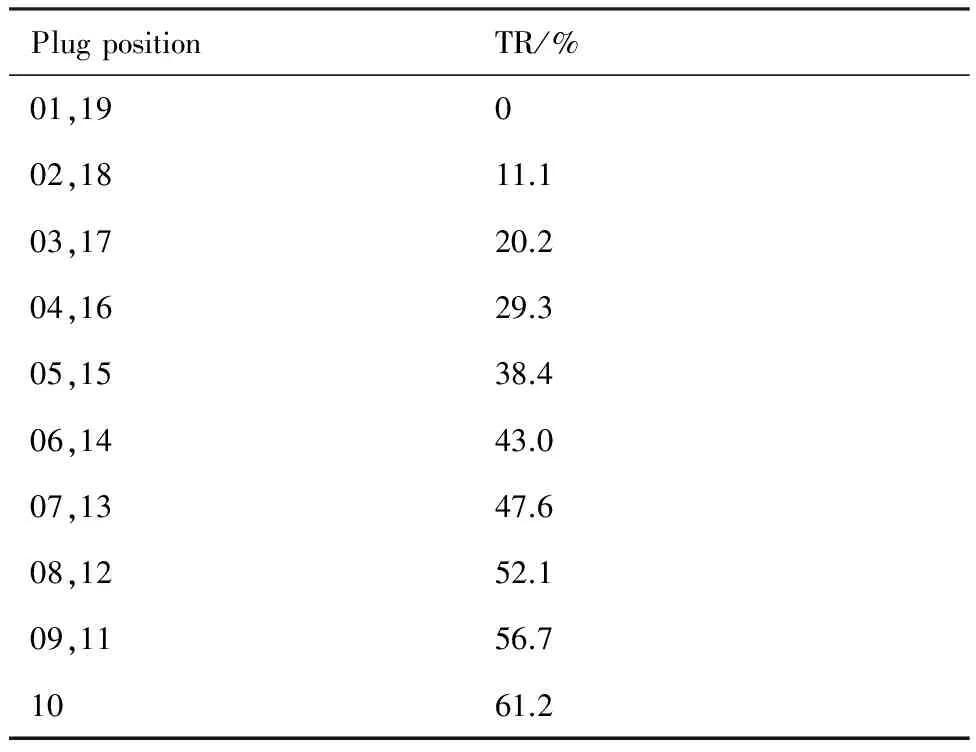
表3 锥位和对应的堵塞度

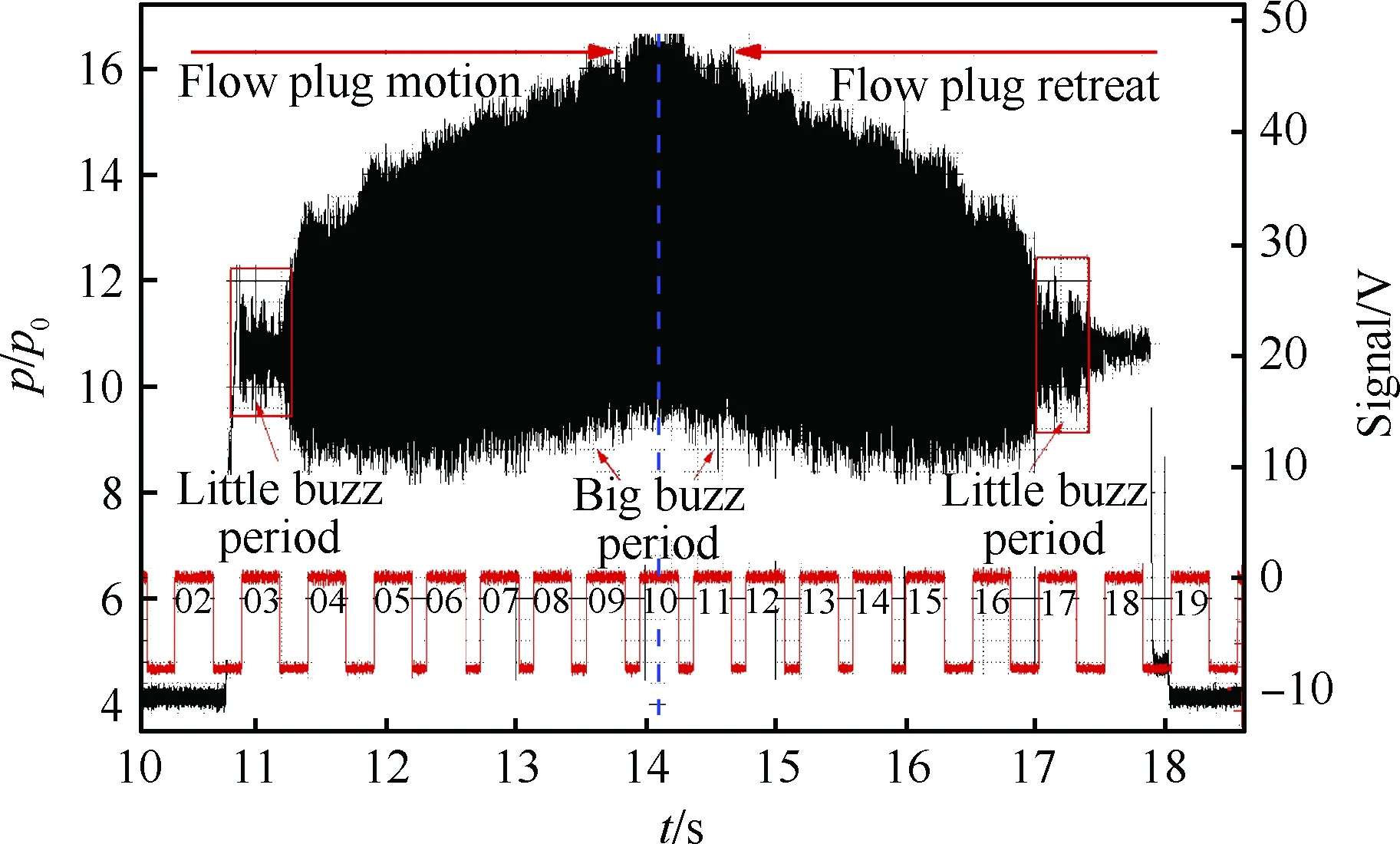
图12 -6°攻角下再起动过程D7测点压强信号和 电机控制信号的时间历程Fig.12 Pressure time histories of D7 point and motor control signals of restart process at α=-6°

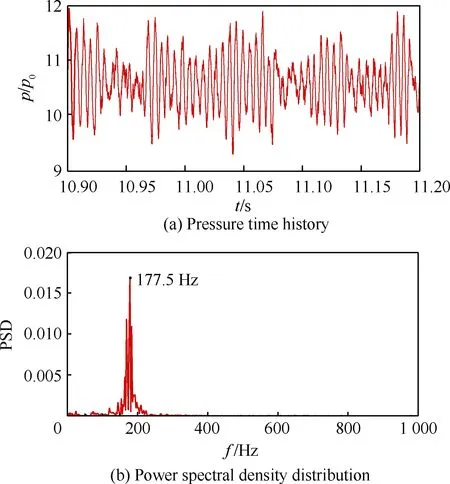
图13 -6°攻角下进气道“小喘”阶段D7测点压力 信号(TR=20.2%)Fig.13 Pressure signals of D7 point for inlet at α=-6° during little buzz period (TR=20.2%)

图14 -6°攻角下进气道“小喘”不起动流场 结构(TR=20.2%)Fig.14 Unstart flow pattern of inlet at α=-6° during little buzz period (TR=20.2%)

随着堵塞度的增大，进气道出口流动壅塞程度加剧，进气道进入到“大喘”振荡阶段。无论是其通道内的压力脉动量(图12)还是口外不起动波系运动幅度均将得到大幅增长(图16)。由上文可知，近年来国内外的学者对“大喘”振荡现象和机理的研究已开展了大量的研究工作，并取得了一定的共识。其中，Tan[16]提出了一种以进口溢流量为扰动源，对流、激波串运动和声波3种扰动传播方式相互接力构成的扰动信号闭环模式。然而由于该部分并不是本文的研究重点，因此本文在这就不再进行过多的赘述。

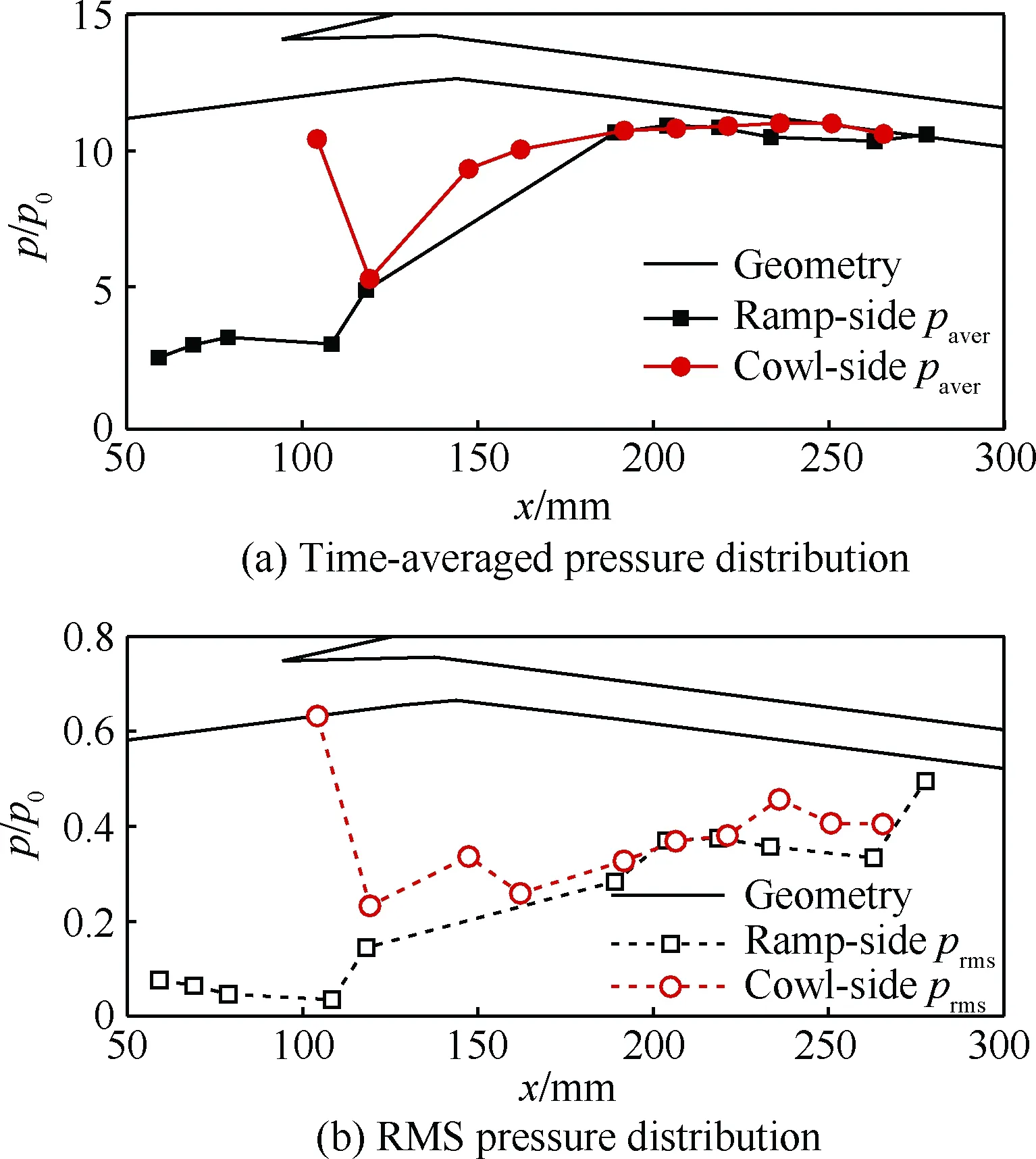
图15 -6°攻角下进气道“小喘”不起动阶段 静压分布(TR=20.2%)Fig.15 Distribution of static pressure of unstart inlet at α=-6° during little buzz period (TR=20.2%)

依照表3中的锥位和堵塞度对应关系可见，当堵锥前进至第10个锥位(TR=61.2%)后，堵锥开始回退，也即导致进气道不起动的因素将被逐渐移除，进气道进入到再起动阶段。为了对比在喘振阶段中流场的历史效应和进锥时序的影响，表4中列出了典型喘振锥位下的D7测点喘振特性参数。可以看到在出现“大喘”的堵塞度下，D7测点的压力脉动特性无论是振荡基频、时均值还是脉动均方根值均只决定于此刻的堵塞度，与其历史锥位无关。然而在“小喘”堵塞度(TR=20.2%)下，进锥时(锥位03)和退锥时(锥位17)的压力脉动特性却出现了偏差，虽然此时两者均保持着稳定的振荡，但是退锥时的压力脉动量和频率要明显大于进锥时的。

然而存在于上述两个“小喘”锥位中振荡特性的偏差，在其各自的下一个对称锥位02和锥位18中得到了放大。结合图13可以看到，进锥锥位02通道最下游测点仍未受到下游高压的干扰，其流场结构和沿程压力特性和通流流场相同。然而在同样堵塞度下的退锥锥位18却出现了明显的压力振荡。可见在进气道从之前的“小喘”喘振状态恢复至起动流场前，流场出现了迟滞现象。对此，接下来将进一步对比分析“小喘”锥位17和迟滞锥位18的流场结构和振荡特性，以增进对该类现象的理解和认识。

图16 -6°攻角下进气道“大喘”不起动流场 结构(TR=61.2%)Fig.16 Unstart flow pattern of inlet at α=-6° during big buzz period (TR=61.2%)

表4 典型喘振锥位下的D7测点喘振特性参数Table 4 Characteristic parameters of typical plug positions under buzz state

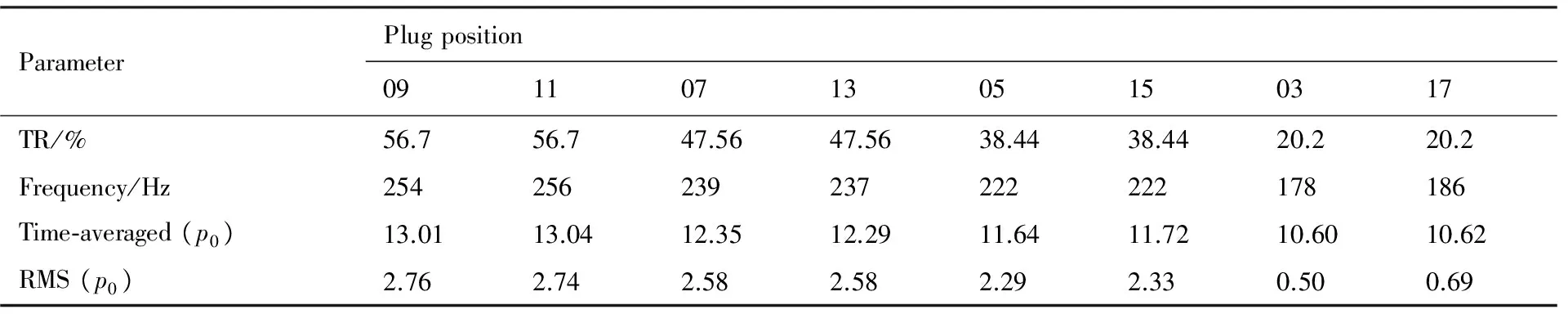
ParameterPlugposition0911071305150317TR/%56．756．747．5647．5638．4438．4420．220．2Frequency/Hz254256239237222222178186Time⁃averaged(p0)13．0113．0412．3512．2911．6411．7210．6010．62RMS(p0)2．762．742．582．582．292．330．500．69

图17 -6°攻角进气道锥位18下流场结构 (TR=11.1%)Fig.17 Flow pattern of inlet at α=-6°,plug 18 (TR=11.1%)

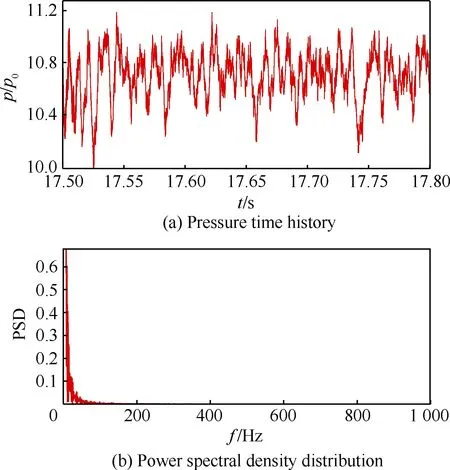
图18 -6°攻角进气道锥位18下D7测点压力信号 (TR=11.1%)Fig.18 Pressure signals of D7 point of inlet at α=-6°,plug 18(TR=11.1%)

首先，图17中给出了锥位18下对应的振荡流场结构，对比之前的“小喘”振荡流场(图14)可见，两者均表现为口部分离诱导激波在进口处的小幅振荡，但是其激波振荡幅度较“小喘”阶段有所减弱。而在压力信号方面，图18给出了锥位18下D7测点的压力时间曲线及其功率谱密度分布，可见锥位18下的压力信号并未出现如之前“小喘”时的周期性压力振荡，反而呈现出一种类似上文所描述的低马赫数不起动中出现的无规律振荡。更进一步的，图19对比给出了锥位17和锥位18下的沿程压力时均值和脉动值分布曲线，可以看到在时均值分布上，2个锥位基本重合，只是在进口段分离包位置，由于其分离包振荡幅度的减小，锥位18的压力时均值要略低于锥位17。然而两者在压力脉动值分布规律上却相差较大(图19(b))，尤其在进气道通道内，锥位17呈现为沿程递增的变化趋势，而锥位18则整体维持在一个较低值(0.13p0)。可见在锥位18时，进气道通道下游并未形成类似锥位17的流动壅塞，因此无法对上游分离包产生的扰动进行放大和反馈，进而无法建立周期性振荡。并且锥位18的沿程压力脉动值分布和低马赫不起动状态的分布(图3)非常相似，其沿程压力脉动峰值均出现在喉道附近，且通道内压力脉动值也维持在一个较低值附近(0.1p0)。

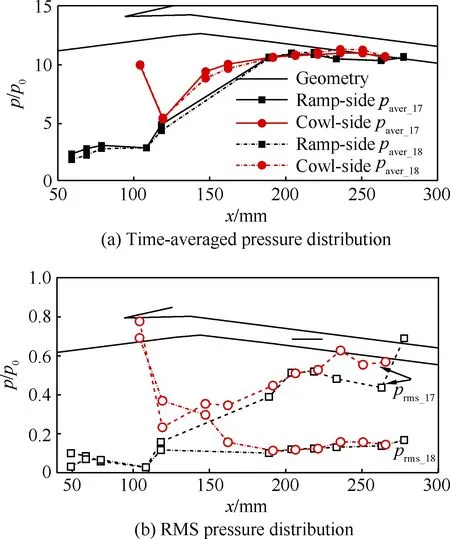
图19 锥位17及锥位18下压力分布对比Fig.19 Comparison of pressure distribution under plug 17 and plug 18

综上可知，随着堵锥不断回退，在进气道从“小喘”状态向起动状态过渡的过程中，将先跳出“小喘”振荡阶段进入到类似低马赫不起动的口部分离包自激振荡阶段，同时在该过程中捕捉到了口部分离包吞入的迟滞现象。之后伴随着堵锥的继续回退，口部分离包被吞入通道内，进气道才恢复到初始的完全起动状态。并且可以看到此时和初始通流状态的沿程压力分布基本完全重合(图20)，也就是说该进气道在此状态下能够顺利的再起动。

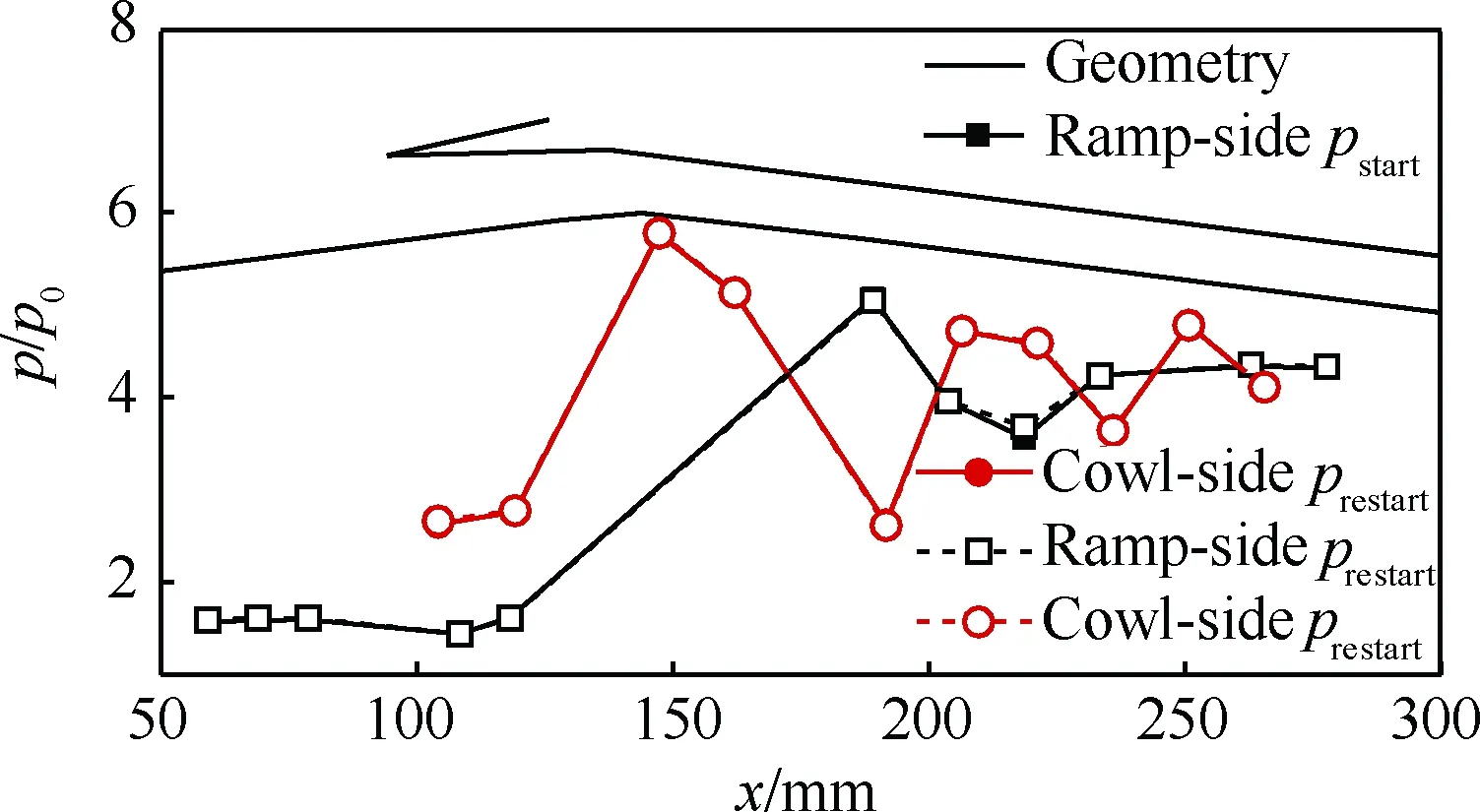
图20 -6°攻角下进气道起动和再起动时刻压力时 均值分布Fig.20 Time-averaged pressure distribution during inlet start and restart at α=-6°

5 结 论

1) 试验结果表明，当进气道处于低马赫数不起动时，在进气道口部形成了一个巨大的分离包，该分离包的诱导激波受分离包自身振荡特性的影响，在唇口附近连续的小幅振荡，进而给整个进气道通道内引入了一类无基频的小幅压力扰动。

2) 随着进气道进口马赫数的增大，进气道口部分离包逐渐缩小并回退至通道内，进气道从不起动状态过渡至起动状态。并在临界状态下，还捕捉到了进气道口部分离包被完全吞入实现完全起动的动态过程。

3) 当进气道处于“小喘”状态时，虽然其小幅的振荡流场结构和低马赫数不起动流场结构相似，但是由于通道下游形成的壅塞构成了扰动反馈回路，因此其通道内的压力振荡表现出了明显的振荡频率特性。

4) 在进气道再起动过程中的分离包吞入阶段捕捉到了迟滞现象，进气道从“小喘”阶段恢复至起动状态时，由于下游高压的存在使得分离包未能完全吞回，流场出现了类似低马赫不起动时的无基频小幅振荡。最后该振荡随着通道下游完全敞开、口部分离包的吞入而逐渐消失，进气道也顺利地恢复到了起动状态。

[1] CURRAN E T, MURTHY S N B. Scramjet propulsion[M]. Reston, VA: AIAA Education Series, 2001: 447-511.

[2] MCCLINTON C R, HUNT J L. Airbreathing hypersonic technology vision vehicles and development dreams[C]∥9th International Space Planes and Hypersonic Systems and Technologies Conference. Reston, VA: AIAA, 1999.

[3] VOLAND R T, AUSLENDER A H,SMART M K.CIAM/NASA Mach 6.5 scramjet flight and ground test[C]∥9th International Space Planes and Hypersonic Systems and Technologies Conference. Reston, VA: AIAA, 1999.

[4] WALKER S, RODGERS F, PAULL A, et al. HyCAUSE flight test program[C]∥15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference. Reston, VA: AIAA, 2008.

[5] MUSIELAK D. High speed air breathing propulsion 2010, moving faster towards the future[C]∥AIAA HSABP TC Communications. Reston, VA: AIAA, 2010.

[6] OSWATITSCH K. Pressure recovery for missiles with reaction propulsion at high supersonic speeds:TM 1140[R]. Washington,D.C.: NACA, 1944.

[7] NEWSOME R W. Numerical simulation of near-critical and unsteady, subcritical inlet flow[J]. AIAA Journal, 1984, 22(10): 1375-1379.

[8] LU P J, JAIN L T. Numerical investigation of inlet buzz flow[J]. Journal of Propulsion and Power, 1998, 14(1): 90-100.

[9] TRAPIER S, DUVEAU P, DECK S. Experimental study of supersonic inlet buzz[J]. AIAA Journal, 2006, 44(10): 2354-2365.

[10] TRAPIER S, DECK S, DUVEAU P. Time frequency analysis and detection of supersonic inlet buzz[J]. AIAA Journal, 2007, 45(9): 2273-2284.

[11] TRAPIER S, DECK S, DUVEAU P. Delayed detached-eddy simulation and analysis of supersonic inlet buzz[J]. AIAA Journal, 2008, 46(1): 118-131.

[12] LEE H J, LEE B J, KIM S D, et al. Flow characteristics of small-sized supersonic inlets[J]. Journal of Propulsion and Power, 2011, 27(2): 306-318.

[13] SOLTANI M R, FARAHANI M. Effects of angle of attack on the inlet buzz[J]. Journal of Propulsion and Power, 2012, 28(4): 747-757.

[14] HERRMANN D, SIEBE F, GÜLHAN A. pressure fluctuations (buzzing) and inlet performance of an airbreathing missile[J]. Journal of Propulsion and Power, 2013, 29(4): 839-848.

[15] SCOTT D H. Wind-tunnel blockage and actuation systems test of a two-dimensional scramjet inlet unstart model at Mach 6: TM-1994-109152[R]. Washington,D.C.: NASA, 1994.

[16] TAN H J, SUN S, YIN Z L. Oscillatory flows of rectangular hypersonic inlet unstart caused by downstream mass-flow choking[J]. Journal of Propulsion and Power, 2009, 25(1): 138-147.

[17] TAN H J, LI L G, WEN Y F, et al. Experimental investigation of the unstart process of a generic hypersonic inlet[J]. AIAA Journal, 2011, 49(2): 279-288.

[18] WAGNER J L, VALDIVIA A, CLEMENS N T, et al. Experimental investigation of unstart in an inlet/isolator model in Mach 5 flow[J]. AIAA Journal, 2009, 47(6): 1528-1542.

[19] WAGNER J L, YUCEIL K B, CLEMENS N T. Velocimetry measurements of unstart in an inlet-isolator model in mach 5 flow[J]. AIAA Journal, 2010, 48(9): 1875-1888.

[20] LI Z F, GAO W Z, JIANG H L, el al. Unsteady behaviors of a hypersonic inlet caused by throttling in shock tunnel[J]. AIAA Journal, 2013, 51(10): 2485-2492.

[21] CHANG J T, WANG L, BAO W, et al. Novel oscillatory patterns of hypersonic inlet buzz[J]. Journal of Propulsion and Power, 2012, 28(6): 1214-1221.

[22] ZHANG Q F, TAN H J, SUN S, et al. Unstart of a hypersonic inlet with side compression caused by downstream choking[J]. AIAA Journal, 2016, 54(1): 28-38.

[23] JIAO X L, CHANG J T, WANG Z Q, et al. Mechanism study on local unstart of hypersonic inlet at high Mach number[J]. AIAA Journal, 2015, 53(10): 3102-3112.

[24] ZHANG Q F, TAN H J, CHEN H, et al. Unstart process of a rectangular hypersonic inlet at different speeds[J]. AIAA Journal, 2016, 54(12): 3681-3691.

[25] 袁化成, 梁德旺. 高超声速进气道再起动特性分析[J]. 推进技术, 2006, 27(5): 390-393.

YUAN H C, LIANG D W. Analysis of characteristics of restart performance for a hypersonic inlet[J]. Journal of Propulsion Technology, 2006, 27(5): 390-393 (in Chinese).

[26] 王卫星, 郭荣伟. 高超声速进气道自起动过程中流动非定常特性[J]. 航空学报, 2015, 36(10):3263-3274.

WANG W X, GUO R W. Unsteady flow characteristics of hypersonic inlet during self-starting[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(10): 3263-3274 (in Chinese).

[27] 常军涛, 于达仁, 鲍文. 迎角引起的高超声速进气道不起动/再起动特性分析[J]. 航空动力学报, 2008, 23(5): 816-821.

CHANG J T, YU D R,BAO W. Characteristic analysis of unstart/restart of hypersonic inlets caused by variations of attack angle of freestream[J]. Journal of Aerospace Power, 2008, 23(5): 816-821 (in Chinese).

[28] 谢旅荣, 郭荣伟. 一种定几何混压式二元进气道的再起动特性研究[J]. 航空动力学报, 2008, 23(2): 389-395.

XIE L R, GUO R W. Investigation of the restart performance of a mixed-compression two-dimensional supersonic inlet with fixed-geometry[J]. Journal of Aerospace Power, 2008, 23(2): 389-395 (in Chinese).

[29] 刘凯礼. 高超声速进气道动/稳态迎角特性研究[D]. 南京：南京航空航天大学, 2011.

LIU K L. Research of aerodynamic characteristics of hypersonic inlets with dynamic/steady angle-of-attack[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2011 (in Chinese).

[30] PIPONNIAU S, DUSSAUGE J P, DEBIEVE J F, et al. Simple model for low frequency unsteadiness in shock induced separation[J]. Journal of Fluid Mechanics, 2009, 629: 87-108.

TestoflowMachnumberunstartandrestartprocessesofhypersonicinlet

WANGChenxi1，TANHuijun1，*，ZHANGQifan1，SUNShu2

1.JiangsuProvinceKeyLaboratoryofAerospacePowerSystem,CollegeofEnergyandPowerEngineering，NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China2.CollegeofCivilAviation,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China

Toenrichtheunderstandingofthemechanismforhypersonicinletunstart,awindtunneltestisconductedtoinvestigatethelowMachnumberunstartandrestartofatruncatedtwo-dimensionalhypersonicinlet.Byvaryingtheinletangleofattackandthedownstreamchokingdegree,thevariationoftheinletflowMachnumberandheatreleaseofcombustioninrealflightconditionsaresimulatedinthistest.Thehigh-speedSchlierenimagingtechnologyandtime-resolvedpressuremeasurementsareusedtorecordtheinstantaneousflowpatternandsurfacepressuresignals.TheresultsshowthatduringtheunstartprocessatlowMachnumber,theseparationbubbleinducedobliqueshockisinfluencedbytheoscillationcharacteristicoftheseparationbubble,andoscillatesslightlyaroundthecowlliptointroduceatypeofsmall-amplitudedisturbancewithoutbasefrequency.ThisdisturbancegraduallydisappearswiththeincreaseoftheMachnumberandrestartoftheinlet.Hysteresisofswallowofseparationbubbleisalsoobservedinthetest.Whentheinletrecoveriesfromthelittlebuzzlestatetothestartstate,theseparationbubblecannotbefullyswallowedduetothepresenceofhighpressuredownstreamduringtherestartprocess,andexhibitsasasmall-amplitudeoscillationsimilartotheoneinlowMachnumberunstartprocess.Theoscillationdoesnotdisappearuntiltheinletexitisfullyopenandtheseparationbubbleintheentranceisswallowedsimultaneously,andthentheinletreturnstostartsuccessfully.

hypersonicinlet;lowMachnumber;unstart;restart;hysteresis

2017-01-18；Revised2017-02-09；Accepted2017-03-20；Publishedonline2017-04-111021

URL：http://hkxb.buaa.edu.cn/CN/html/20171104.html

NationalNaturalScienceFoundationofChina(11532007)

.E-mailtanhuijun@nuaa.edu.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6983.2017.121146

V211.3

A

1000-6893(2017)11-121146-12

2017-01-18；退修日期2017-02-09；录用日期2017-03-20；< class="emphasis_bold">网络出版时间

时间：2017-04-111021

http://hkxb.buaa.edu.cn/CN/html/20171104.html

国家自然科学基金(11532007)

.E-mailtanhuijun@nuaa.edu.cn

王晨曦，谭慧俊，张启帆,等.高超声速进气道低马赫数不起动和再起动试验J. 航空学报，2017,38(11):121146.WANGCX,TANHJ,ZHANGQF,etal.TestoflowMachnumberunstartandrestartprocessofhypersonicinletJ.ActaAeronauticaetAstronauticaSinica,2017,38(11):121146.

(责任编辑：张晗)