基于高精度模态气动力的跨声速静弹高效分析方法

何飞，洪冠新，刘海，但聃，王明

1.北京航空航天大学 航空科学与工程学院，北京 100083 2.中航工业成都飞机设计研究所，成都 610000

基于高精度模态气动力的跨声速静弹高效分析方法

何飞1, 2,*，洪冠新1，刘海2，但聃2，王明2

1.北京航空航天大学 航空科学与工程学院，北京 100083 2.中航工业成都飞机设计研究所，成都 610000

跨声速静弹分析一直是工程设计中的难点问题，以模态坐标系下的线性静弹方程为基础，提出了基于高精度模态气动力的跨声速静弹高效分析方法，该方法仍需求解线性静弹方程，但对于其中关键的模态变形引起的弹性气动力增量，采用由结构变形到气动力的单向计算流体动力学(Computational Fluid Dynamics, CFD)/计算结构动力学(Computational Structural Dynamics, CSD)耦合方法获得，实现了高效线性方法与高精度CFD/CSD耦合方法的有效融合。以某小展弦比机翼基本状态、舵偏状态以及某型战斗机跨声速副翼效率的静弹分析为例，对比分析了本文方法、经典线性方法、CFD/CSD耦合方法的计算结果以及某型机的试飞辨识结果。分析结果表明，所提出的方法在计算效率、精度和鲁棒性方面具备综合优势，具有较高的工程应用价值。

气动弹性；跨声速；结构模态；CFD/CSD耦合；副翼效率；试飞辨识

静气动弹性(简称静弹)是现代飞机设计中的重要研究内容，其分析结果对飞行控制及飞行载荷设计均有重要影响。目前，静弹分析的主要方法包括基于面元气动力的线性方法以及基于计算流体动力学(Computational Fluid Dynamics, CFD)/计算结构动力学(Computational Structural Dynamics, CSD)的耦合迭代方法[1-2]。

线性方法的主要特点是将结构变形引起的弹性气动力增量通过气动力影响系数(Aerodynamic Influence Coefficients，AIC)矩阵求得，该矩阵一般通过低阶或高阶面元法获得，因此，弹性气动力增量和结构变形之间呈线性关系，两者可通过求解静弹方程同时获得，计算过程无需迭代，求解效率高，主要适用于以线性气动力为主导的亚声速和超声速的静弹分析，对于跨声速等以非线性气动力为主导的静弹问题，其分析精度往往难以令人满意[3]。

CFD/CSD耦合方法对于结构变形引起的弹性气动力增量采用求解Euler或Navier-Stokes方程获得，气动力计算精度高，适用于包括跨声速在内的各速度域下的静弹分析，但由于弹性气动力增量和结构变形之间为非线性关系，因此，需要在CFD和CSD之间耦合迭代求解，这使得计算过程较为复杂、效率较低，不适用于工程上的大规模计算，且由于计算过程中要对CFD计算用到的网格进行大量的变形操作，也容易出现网格变形失败等鲁棒性差的问题。

基于上述特点，虽然CFD/CSD耦合方法精度更高且已经发展得较为成熟，但考虑到计算效率、鲁棒性等问题，目前工程设计中仍然主要采用基于线性理论的方法进行跨声速静弹分析。

为解决上述工程问题，提高线性方法在跨声速下的静弹分析精度，国内外开展了很多研究。在国内，杨超等[4]将高阶面元法用于静弹分析，提高了气动力计算的精确性，但由于采用的仍然是线性气动力，因此，该方法主要用于初步设计阶段的静弹分析;万志强等[5-7]将非线性试验气动力引入线性静弹方程并采用了经匹配性插值后的AIC矩阵，在工程上取得了相对较好的应用效果。在国外，主要研究方向集中在提高线性方法中影响气动力计算精度的核心因素——AIC矩阵的精度上，采用的主要方法为通过匹配基于AIC的理论气动力和外部刚体气动力(试验/CFD计算气动力)反求出一个修正矩阵，由此进一步获得弹性变形引起的气动力增量。该修正矩阵一般有2种形式：①对角阵，该矩阵为通过匹配某单一状态(如迎角状态)的气动力获得，不适用于其他状态的分析[8-9]；②非对角阵,该矩阵为通过同时匹配多种状态(如迎角状态、舵偏状态等)气动力获得，相比于对角矩阵，该方法适应范围大大增加，但所求得的矩阵依赖于对所匹配气动力状态的选择[10]。

本文基于模态坐标系下的线性静弹方程提出一种新方法，其主要思路为：弹性模态变形下的跨声速弹性气动力增量不再通过线性面元法或基于外部刚体气动力修正AIC矩阵来获得，而是基于从结构变形到气动力的单向CFD/CSD耦合方法直接求解得到，由此实现了线性方法与CFD/CSD耦合方法的有效融合，从而达到高效、具有鲁棒性与高精度的效果,适用于小变形下的跨声速静弹分析。进一步地,本文以某小展弦比机翼基本状态、舵偏状态以及某型战斗机跨声速副翼效率的静弹分析为例，对比分析了线性方法、CFD/CSD耦合方法、本文方法的计算结果以及某型机的试飞辨识结果，分析结果表明本文方法在计算效率、精度和鲁棒性方面具备综合优势，具有较高的工程应用价值。

1 基于高精度模态气动力的静弹分析

模态坐标系下基于线性气动力的静气动弹性分析方程一般可写为[11]

(φTKφ-QSφTAICφ′)q=φTF

(1)

式中：K为结构刚度矩阵；AIC为气动力影响系数矩阵；F为外部刚体气动力；φ、φT、φ′分别为结构弹性模态向量矩阵及其转置、导数矩阵；Q为来流动压；S为气动面元的面积矩阵；q为广义坐标向量。

式(1)中QSφTAICφ′q即为由于结构弹性变形引起的气动力增量，该增量的准确求解是跨声速静弹分析的核心难点，也是跨声速静弹分析误差的主要来源。

为提高分析精度，考虑到Q、S、φ是仅依赖于来流条件、几何外形及结构特性的已知量，因此，如引言中所述，目前的方法主要是通过采用各种措施提高AIC的计算精度，本文从另一个角度出发，提出了一种新的解决思路，即把气动力增量项QSφTAICφ′q中的AICφ′作为一个整体项来考虑，该项实质上就是各阶结构弹性模态引起的气动力增量，将其表示为

ΔCpmod=AICφ′

(2)

式中：ΔCpmod即为模态气动力增量矩阵，此项可以采用更高精度的方法来获得。本文即通过CFD/CSD耦合方法来获得高精度的模态气动力增量，且由于仅需要计算刚性外形和基于模态变形的弹性外形下的刚体气动力，将两者相减即可获得模态气动力增量矩阵，无需迭代，因此，这里的CFD/CSD耦合仅是一次根据结构弹性变形计算弹性气动力的单向耦合，其精度取决于CFD的计算精度。将获得的高精度弹性气动力增量代入式(1)后将显著提高静弹计算精度，由此式(1)可写为

(φTKφ-QSφTΔCpmod)q=φTF

(3)

对比式(1)和式(3)，可知，式(3)仍然求解线性静弹方程，但关键的弹性气动力增量由CFD/CSD单向耦合计算得到，这显著提高了模态变形对气动力影响的计算精度，尤其是跨声速时，可以计及气动力非线性以及变形对局部激波强度、位置的影响，这对跨声速静弹分析尤为关键，从而实现了高效具有鲁棒性的线性方法与高精度非线性方法的有效融合。

需要注意的是，由于求解的仍然是线性方程，因此，该方法中实质上作了局部线化的假设，即弹性气动力增量对弹性变形量的导数为常值，这在小变形情况下是适用的，用于柔性大变形情况时，由于弹性变形引起的局部迎角变化较大，这一导数不再为常值，会引起较大的误差。

2 高精度模态气动力的计算

本文采用CFD/CSD单向耦合方法求解非线性模态气动力，具体流程如图1所示。根据图1中的流程，主要操作步骤如下：

步骤1根据确定的分析状态，生成CFD计算网格，获得刚性外形下的气动力分布。

步骤2将弹性模态变形通过曲面插值方法[12]插值到CFD表面气动网格，根据变形后的表面网格,基于径向基函数插值方法[13-15]并采用贪婪算法等高效处理方法[16-19]获得弹性CFD计算网格，进而获得各阶模态变形下的弹性气动力分布。

步骤3将刚性和弹性分布气动力的差量通过无限平板插值(IPS)方法[20]插值到面元网格上，由此获得式(3)中的高精度弹性气动力增量矩阵ΔCpmod。

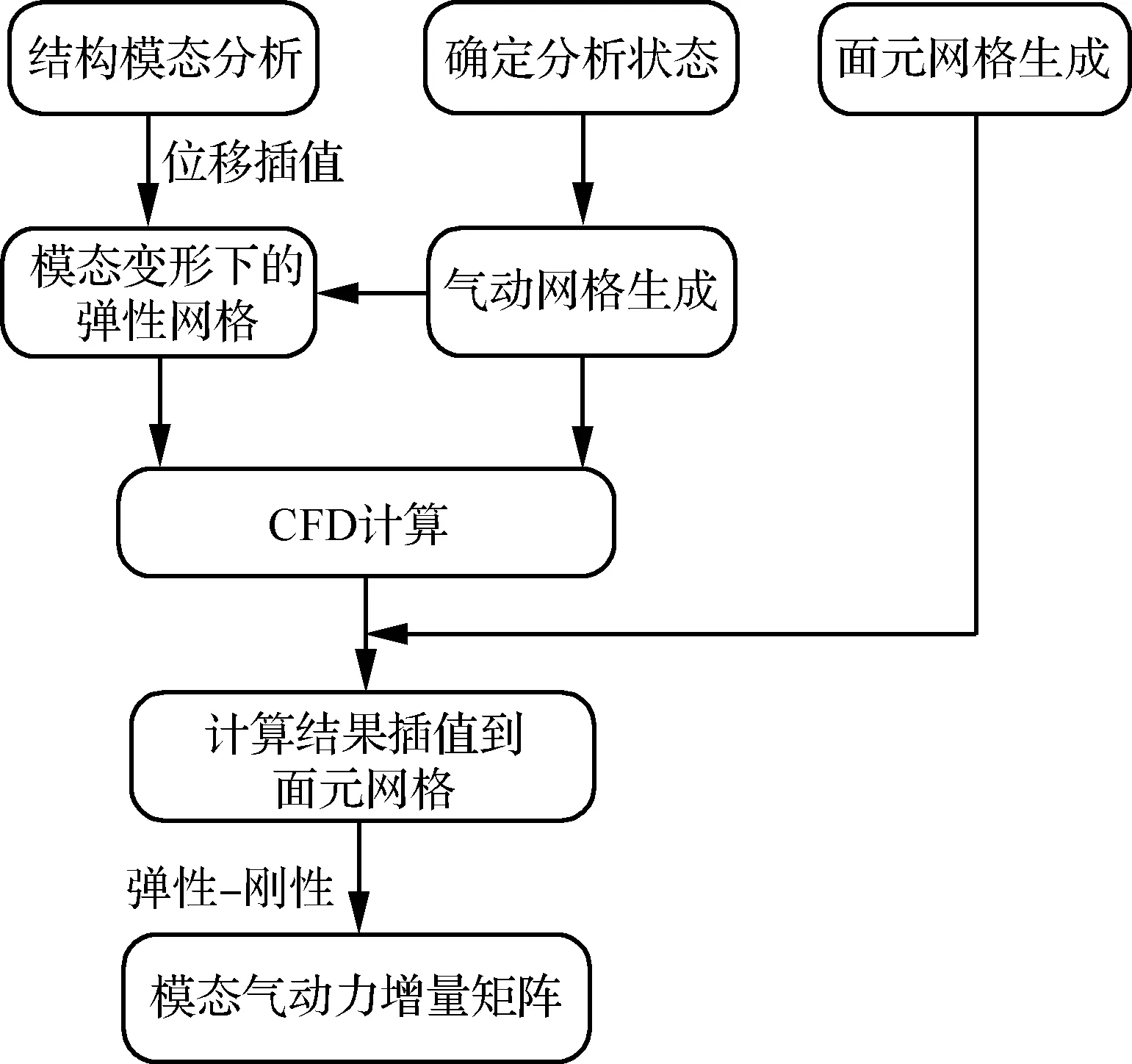
图1 非线性模态气动力计算流程图Fig.1 Computation flow chart of nonlinear modal aerodynamics

2.1 模态及变形量的确定

在图1所示的计算流程中，需要多阶模态以及相应模态具体的变形量，以和基本状态外形叠加得到计算外形。

关于模态数目，根据经典模态法静弹分析的经验，取30～50阶弹性模态即可获得足够精度。

关于模态的具体变形量，分析式(3)可知，该方法实质上是将各阶模态变形对气动力的影响作为小扰动项，最终弹性变形的影响量需要由各小扰动项线性叠加得到，因此，这里的模态变形不宜过大。本文采用MSC.Nastran中基于Lanczos方法并以质量归一化后输出的模态数据。

2.2 基本状态的确定

基本状态的确定对模态气动力的计算有重要影响，其内容包括:①计算外形的确定，即舵偏状态；②基本计算参数的确定，即迎角和侧滑角。

从理论上分析，上述外形以及参数应该根据式(3)中外部刚体气动力F的状态参数来确定，这样得到的模态气动力最为合适，用于静弹计算的精度也最高，如果状态参数不一致，将导致静弹计算精度下降，误差随状态参数差异的增加而增大。

由上述分析可知，对于气动导数或某一特定状态的静弹分析，由于外部刚体气动力F的状态参数是单一的，因此，完全可以根据F的状态参数来确定基本状态。但用于工程设计时，由于F的状态众多，完全根据F的状态来确定基本状态将导致模态气动力的计算量过大，此时，可以采用一组较为稀疏的迎角、侧滑角、舵偏参数向量计算出模态气动力数据库，在静弹分析时，根据外部刚体气动力F的状态参数从该数据库中插值得到相应的模态气动力。

3 算例及验证

为充分验证本文方法的计算效果，分别对一小展弦比机翼的基本状态、舵面偏转状态以及某型战斗机副翼效率进行了静弹分析，并和经典线性方法、CFD/CSD耦合方法以及试飞辨识结果进行了比较。

3.1 机翼基本状态的静弹分析

小展弦比机翼外形如图2所示，机翼后缘外侧布置了一个舵面。采用3种方法进行静弹分析，分别为:①式(1)给出的线性方法；②CFD/CSD耦合迭代方法[21]；③式(3)给出的基于模态气动力的方法。

为便于比较，上述3种方法在分析中采用一致的结构约束条件，方法①及方法③采用统一的面元网格以及外部刚体气动力，该外部刚体气动力以及方法③中的模态气动力均采用CFD/CSD耦合中的基于Navier-Stokes方程的气动力计算方法得到。

模态气动力计算取30阶弹性模态，以舵偏角δ=0°、迎角α=4°为基本状态，模态变形在此状态下叠加，典型弯曲、扭转模态下的网格变形如图3所示(为便于显示，图中模态变形量作了放大处理)。

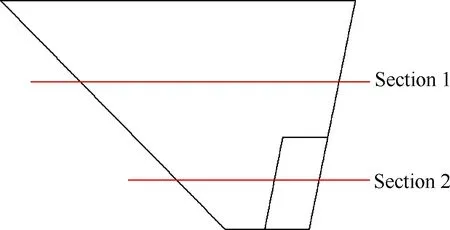
图2 带舵面的机翼外形Fig.2 Layout of wing with control surface

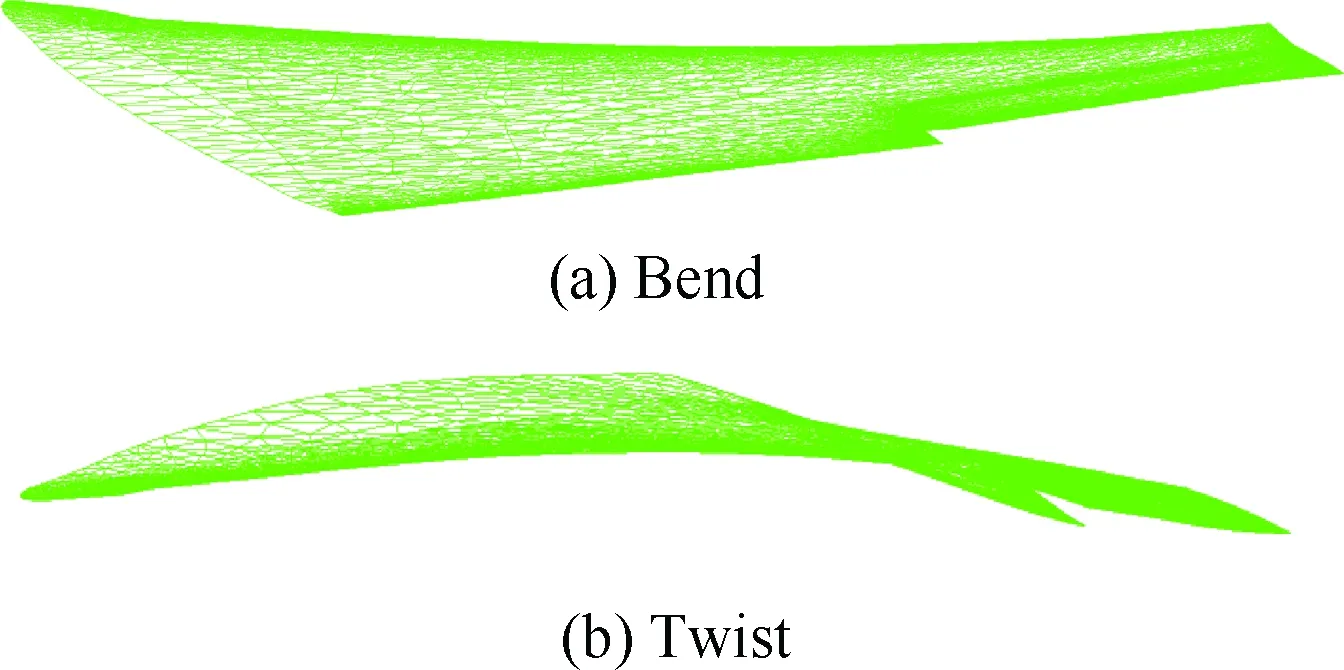
图3 典型模态下的网格变形Fig.3 Mesh deformation of typical structure modes

图4 Ma=0.60、α=4°、H=0 km时压力分布比较Fig.4 Comparison of pressure distributions for Ma=0.60,α=4°, and H=0 km

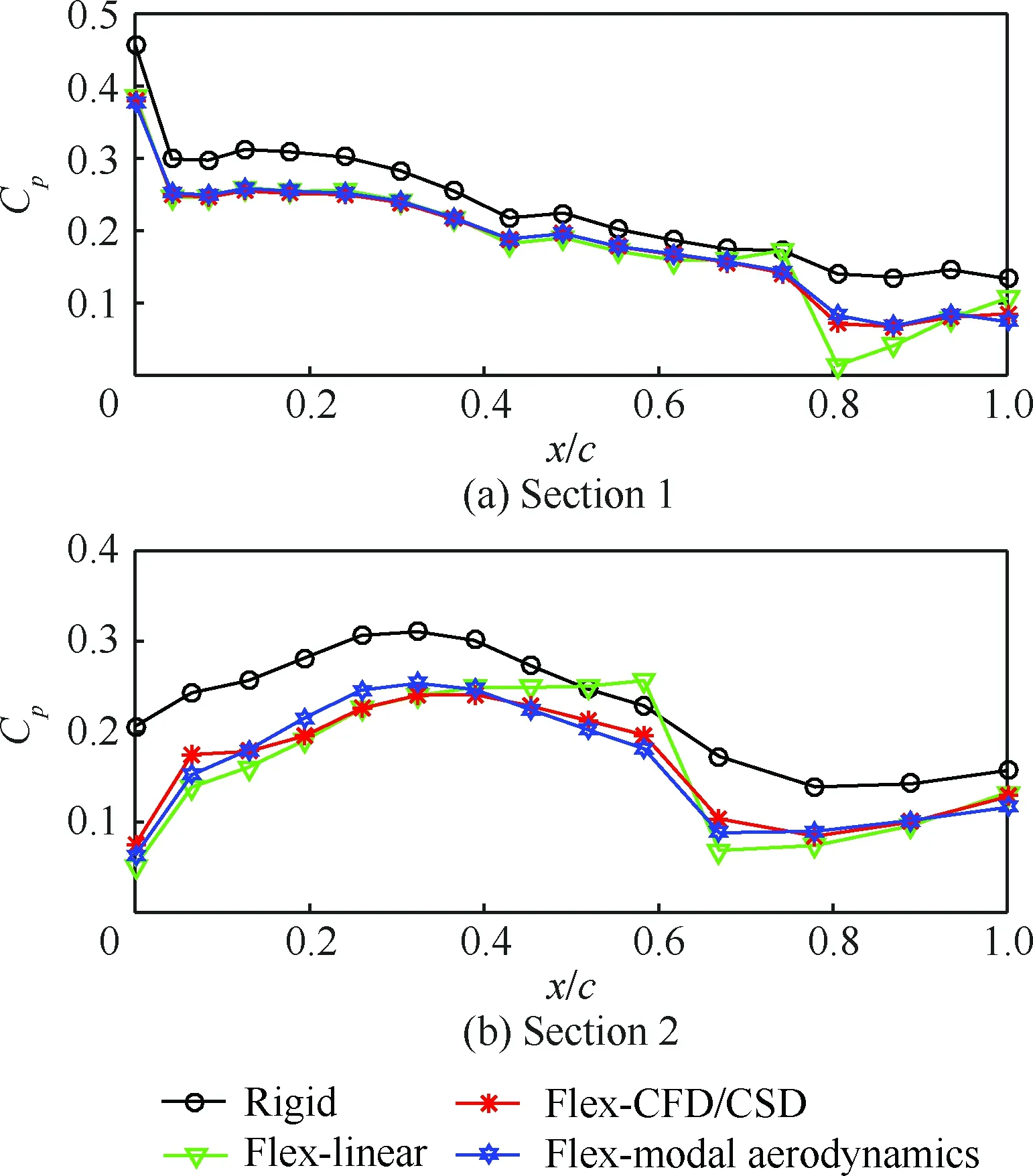
图5 Ma=1.05、α=4°、H=0 km时压力分布比较Fig.5 Comparison of pressure distributions for Ma=1.05, α=4°, and H=0 km

图6 Ma=1.50、α=4°、H=0 km时压力分布比较Fig.6 Comparison of pressure distributions for Ma=1.50, α=4°, and H=0 km

图4～图6分别给出了亚、跨、超声速下(来流马赫数Ma=0.60、1.05、1.50)α=4°、高度H=0 km时典型剖面处的刚性以及分别基于方法①～方法③得到的弹性气动力分布比较,图4～图6中上图和下图分别对应图2中Section 1、Section 2剖面,Cp为压力系数，x/c为无量纲弦长，“Flex”表示弹性，可见：

1) 在亚、超声速下，3种方法得到的弹性气动力结果基本一致。

2) 在跨声速Ma=1.05的情况下，本文方法计算结果和CFD/CSD耦合方法计算结果一致性良好，线性方法则表现出明显的差异。

上述结果符合理论预期，在跨声速区域，基于线性气动力的计算方法精度下降，而本文方法由于采用了高精度的模态气动力，因此，仍可保持和CFD/CSD耦合方法相当的计算精度。

3.2 机翼舵偏状态的静弹分析

图7～图8分别给出了Ma=1.05、α=4°，δ=5°和δ=15°时的压力分布比较，计算机翼及3种计算方法同3.1节,考虑到工程设计中计算状态繁多，难以针对每个状态都建立模态气动力矩阵，因此，有必要考察模态气动力的适用范围，本节中仍然采用δ=0°作为基本状态。由图7和图8可见：

1) 在δ=5°时，基于模态气动力的计算结果和CFD/CSD耦合计算结果基本吻合，但吻合度要弱于图 5中的δ=0°状态，特别是在Section 1剖面处。

2)δ=15°时，基于模态气动力的计算结果和CFD/CSD耦合计算结果出现显著差别，可见，当舵偏角逐渐增大、分析状态逐渐偏离模态气动力计算状态时，局部线化假设不再成立，计算精度出现显著下降。

图7 Ma=1.05、α=4°、δ=5°、H=0 km时 压力分布比较Fig.7 Comparison of pressure distributions for Ma=1.05, α=4, δ=5, and H=0 km

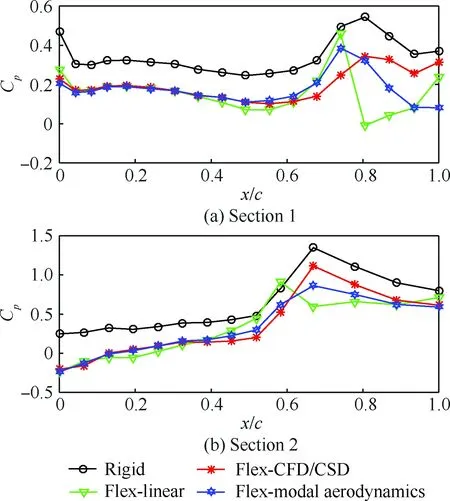
图8 Ma=1.05、α=4°、δ=15°、H=0 km时 压力分布比较Fig.8 Comparison of pressure distributions for Ma=1.05,α =4°, δ=15°, and H=0 km

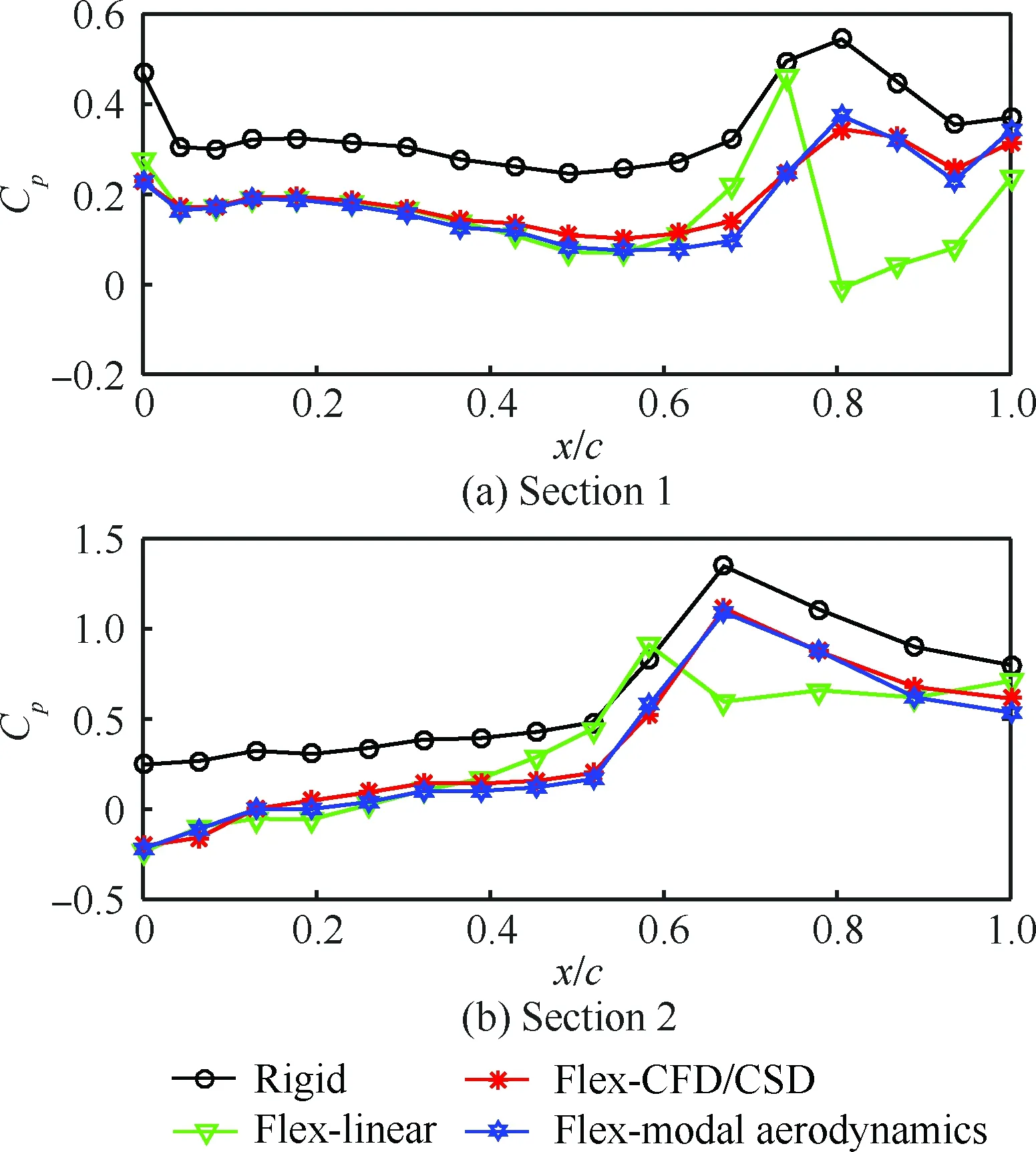
图9 改进后Ma=1.05、α=4°、δ=15°、H=0 km时 压力分布比较 Fig.9 Comparison of pressure distributions for Ma=1.05,α=4°,δ=15°, and H=0 km after modification

上述分析表明，工程上在满足一定精度的条件下，模态气动力的应用范围可以适当扩大，但如果模态气动力计算的基本状态和刚性气动力状态差别较大，将导致分析精度大幅下降，为此，在δ=15°时，模态气动力可以将此状态作为基本状态，将模态变形在此状态下叠加。图9给出了改进后的计算压力分布比较，可见，基于模态气动力的计算精度大幅提高，计算结果和CFD/CSD耦合计算结果吻合良好。

由上述分析可知，基于模态气动力方法的静弹计算精度和刚性气动力、模态气动力计算两者之间的状态差异相关，通过缩小其差异，甚至在跨声速大舵偏状态，本文方法仍可取得和CFD/CSD耦合方法相当的计算精度。

3.3 某型机副翼效率的静弹分析

为进一步验证本文方法在实际工程上的应用效果，应用3.1节中3种方法对某型战斗机跨声速(Ma=0.95)副翼效率进行了分析，其中CFD/CSD耦合方法的具体计算过程见文献[21]，基于模态气动力方法计算时采用30阶模态，模态计算的基本状态为副翼偏度δ=0°，图10给出了不同方法计算得到的副翼滚转效率静弹修正系数K与试飞辨识结果的比较，其中K的定义为

(4)

1) 线性方法给出的修正系数明显偏大，计算精度较低。

2) CFD/CSD耦合方法、基于模态气动力方法的计算结果与试飞辨识结果总体吻合良好，但基于模态气动力方法的计算精度略低于CFD/ CSD耦合方法，这和模态气动力计算以δ=0°作为基本状态相关。

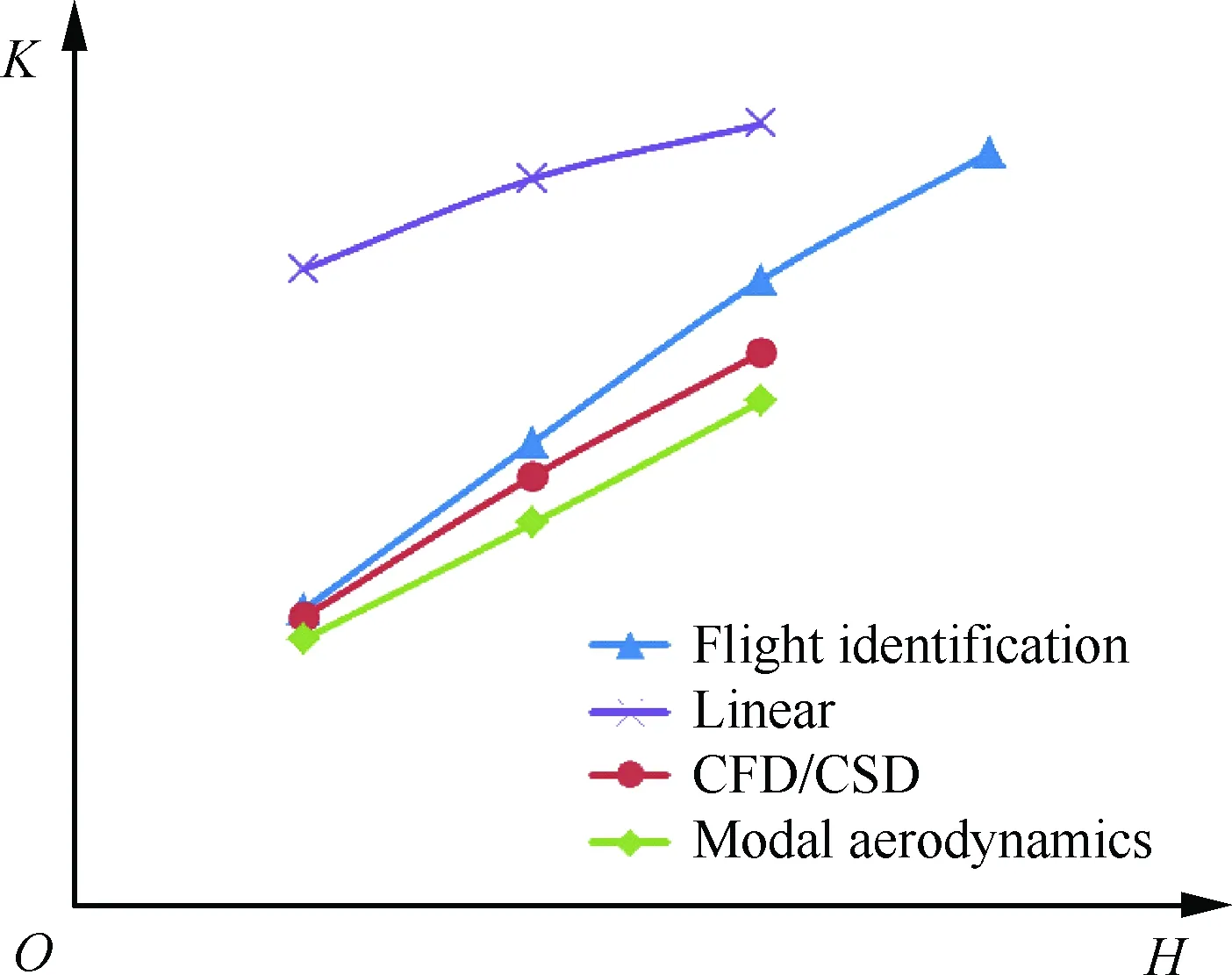
图10 副翼效率静弹修正系数比较(Ma=0.95)Fig.10 Comparison of aileron efficiency static aeroelastic correction coeffcients (Ma=0.95)

3) CFD/CSD耦合方法在处理复杂舵偏状态的网格变形时需采用特殊方法进行(如虚拟网格及虚拟位移等)[21]，以避免计算陷入崩溃，而在模态气动力方法中由于变形量小，网格变形无需特殊处理，具有明显的鲁棒性优势。

4 结 论

本文提出的基于模态气动力的静弹分析方法融合了经典线性方法和CFD/CSD耦合方法的优点，适用于小变形下的跨声速静弹分析，在计算精度、效率、鲁棒性方面具备综合优势，具有较高的工程应用价值：

1) 计算精度。本文方法的计算精度和刚性气动力、模态气动力计算两者之间的状态差异相关，在状态相同或差别不大的情况下，本文方法可取得和CFD/CSD耦合方法相当的计算精度，尤其在跨声速区，计算精度显著大于线性方法。

2) 计算效率。本文方法的计算量主要来源于模态气动力的计算，在获得模态气动力矩阵后，计算效率和线性方法完全相同。由于模态气动力的计算和高度无关，计算过程中无需迭代，而且计算过程独立于静弹计算过程，便于提前准备，综合来看，在工程中大规模计算时，其计算效率低于线性方法，但远高于CFD/CSD耦合方法。

3) 计算鲁棒性。CFD/CSD耦合方法用于工程设计的一个重要问题就是网格变形的鲁棒性问题，本文方法的鲁棒性风险主要来源于各阶模态变形下的网格变形，相比于CFD/CSD耦合方法，本文方法中变形量非常小，且由于无需迭代，无需对网格进行反复变形，显著提高了计算的鲁棒性，可以说基本不存在鲁棒性风险。

[1] PRANANTA B B, MEIJER J J. Transonic static aeroelastic simulations of fighter aircraft: NLR-TP-2003-187[R]. Amsterdam: NLR, 2003.

[2] 张书俊，王运涛，孟德虹. 大展弦比联接翼静气动弹性研究[J].空气动力学学报，2013，31(2): 170-174.

ZHANG S J,WANG Y T,MENG D H.Study on static aeroelasticity for high aspect ratio joinedwings[J]. Acta Aerodynamica Sinica, 2013,31(2): 170-174 (in Chinese).

[3] HEEG J, SPAIN C V, FLORANCE J R,et al. Experimental results from the active aeroelastic wing wind tunnel test program:AIAA-2005-2234[R].Reston, VA: AIAA, 2005.

[4] YANG C, ZHANG B C, WAN Z Q, et al. A method of static aeroelastic analysis based on the high-order panel method and modal method[J]. Science China Technological Sciences, 2011, 54(3): 741-748.

[5] WAN Z Q, ZHANG B C, YANG C, et al. Static aeroelastic analysis of a high-aspect-ratio wing based on wind-tunnel experimental aerodynamic forces[J]. Science China Technological Sciences, 2011, 54(10): 2716-2722.

[6] 万志强, 邓立东, 杨超, 等. 基于非线性试验气动力的飞机静气动弹性响应分析[J]. 航空学报, 2005, 26(4): 439-445.

WAN Z Q, DENG L D, YANG C, et al. Aircraft static aeroelastic response analysis based on nonlinear experimental aerodynamic data[J]. Acta Aeronautica et Astronautica Sinica, 2005, 26(4): 439-445 (in Chinese).

[7] 邵珂, 万志强, 杨超. 基于试验气动力的弹性飞机舵面效率分析[J]. 航空学报, 2009, 30(9): 1612-1617.

SHAO K, WANG Z Q, YANG C. Control surfaces efficiency analysis of flexible aircraft based on experimental aerodynamic forces[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(9): 1612-1617 (in Chinese).

[8] GIESING J P, KALMAN T P, RODDEN W P. Correction factory techniques for improving aerodynamic prediction methods: NASA-CR-144967[R]. Washington, D.C.: NASA, 1976.

[9] JADIC I, HARTLEY D, GIRI J. Improving the aerodynamic approximation in linear aeroelasticity: AIAA-2000-1450[R]. Reston, VA: AIAA, 2000.

[10] MORENO R, NARISETTI R, VON KNOBLAUCH F, et al. A modification to the enhanced correction factor technique to correlate with experimental data: AIAA-2015-1421[R]. Reston, VA: AIAA, 2015.

[11] ZONA Technology Inc. ZAERO theoretical manual V9.2[M]. Scottsdale, AZ：ZONA Technology Inc., 2008：15-25.

[12] XIE C C, YANG C. Surface splines generation and large deflection interpolation[J]. Journal of Aircraft, 2015, 44(3): 1024-1026.

[13] FRANKE R. Scattered data interpolation: Tests of some methods[J]. Mathematics of Computation, 1982,38: 181-200.

[14] ALLEN C B, RENDALL T C S. Unified approach to CFD-CSD interpolation and mesh motion using radial basis functions: AIAA-2007-3804[R]. Reston, VA: AIAA, 2007.

[15] 林言中， 陈兵， 徐旭. 基于径向基函数插值的气动弹性计算方法[J]. 北京航空航天大学学报， 2014， 40(7)： 953-958.

LIN Y Z, CHEN B, XU X. Numerical method of aeroelasticity based on radial basis function interpolation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(7): 953-958 (in Chinese).

[16] SHENG C H, ALLEN C B. Efficient mesh deformation using radial basis functions on meshes[J]. AIAA Journal, 2013, 51(3): 707-720.

[17] RENDALL T C S, ALLEN C B. An efficient fluid-structure interpolation and mesh motion scheme for large aeroelastic simulations: AIAA-2008-6235[R]. Reston, VA: AIAA, 2008.

[18] 王刚， 雷博琪， 叶正寅. 一种基于径向基函数的非结构混合网格变形技术[J]. 西北工业大学学报, 2011, 29(5):784-788.

WANG G, LEI B Q, YE Z Y. An efficient deformation technique for hybrid unstructured grid using radial basis functions[J]. Journal of Northwestern Polytechnical University, 2011, 29(5): 784-788 (in Chinese).

[19] 谢亮, 徐敏, 张斌，等. 基于径向基函数的高效网格变形算法研究[J]. 振动与冲击, 2013, 32(10): 141-145.

XIE L, XU M, ZHANG B, et al. Space points reduction in grid deforming method based on radial basis functions[J]. Journal of Vibration and Shock, 2013, 32(10): 141-145 (in Chinese).

[20] 赵永辉. 气动弹性力学与控制[M]. 北京： 科学出版社, 2007: 45-60.

ZHAO Y H. Aeroelasticity and control[M]. Beijing: Science Press, 2007: 45-60 (in Chinese).

[21] 何飞， 杨超， 但聃， 等. 跨声速副翼效率高精度静弹分析及试飞验证[J]. 北京航空航天大学学报， 2017, 43(3): 457-463.

HE F, YANG C, DAN D, et al. Transonic static aeroelastic analysis of fighter’s aileron efficiecy and test flight verification[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(3): 457-463 (in Chinese).

Efficienttransonicstaticaeroelasticanalysismethodbasedonhighaccuracymodalaerodynamics

HEFei1,2,*,HONGGuanxin1,LIUHai2,DANDan2,WANGMing2

1.SchoolofAeronauticScienceandEngineering,BeihangUniversity,Beijing100083,China2.AVICChengduAircraftDesign&ResearchInstitute,Chengdu610000,China

Transonicstaticaeroelasticanalysishasalwaysbeenadifficultprobleminengineeringdesign.Inthispaper,basedonthelinearstaticaeroelasticequationinthemodalcoordinatesystem,anewefficienttransonicstaticaeroelasticanalysismethodbasedonhighprecisionmodalaerodynamicsisdeveloped.Themethodstillsolvesthelinearequation,butforthekeyaerodynamicincrementscausedbythemodaldeformation,whichcanbeobtainedbytheone-wayCFD(ComputationalFluidDynamics)/CSD(ComputationalStructuralDynamics)interaction.Withthemethod,effectivefusionofhighefficiencylinearmethodandhighaccuracyCFD/CSDinteractionmethodisrealized.Tovalidatetheeffectsofthemethod,staticaeroelasticproblemsofasmallaspectratiowingwith/withoutcontrolsurfaceandtheaileronefficiencyofafighteraircraftareanalyzed,andtheresultsoftheclassicallinearmethod,CFD/CSDinteractionmethodandtestflightidentificationarecompared,whichshowthatthemethoddevelopedhasacomprehensiveadvantageintermsofefficiency,accuracyandrobustness,andhashighengineeringapplicationvalue.

aeroelasticity;transonic;structuremodes;CFD/CSDinteraction;aileronefficiency;testflightidentification

2017-01-22；Revised2017-02-28；Accepted2017-04-03;Publishedonline2017-05-031644

URL：http://hkxb.buaa.edu.cn/CN/html/20171105.html

.E-mailhefei1073@163.com

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.121157

V211.47

A

1000-6893(2017)11-121157-08

2017-01-22；退修日期2017-02-28；录用日期2017-04-03；< class="emphasis_bold">网络出版时间

时间：2017-05-031644

http://hkxb.buaa.edu.cn/CN/html/20171105.html

.E-mailhefei1073@163.com

何飞，洪冠新，刘海，等．基于高精度模态气动力的跨声速静弹高效分析方法J．航空学报,2017,38(11):121157.HEF,HONGGX,LIUH,etal.EfficienttransonicstaticaeroelasticanalysismethodbasedonhighaccuracymodalaerodynamicsJ.ActaAeronauticaetAstronauticaSinica,2017,38(11):121157.

(责任编辑：鲍亚平,王娇)