基于随机有限集的空间碎片群运动状态估计

卢哲俊，胡卫东

国防科学技术大学 电子科学与工程学院 ATR国家重点实验室，长沙 410073

基于随机有限集的空间碎片群运动状态估计

卢哲俊，胡卫东*

国防科学技术大学 电子科学与工程学院 ATR国家重点实验室，长沙 410073

传统的空间目标监测是建立在单目标状态估计基础之上，在面对突发产生的大量空间碎片时，由于碎片尺寸小，且密集分布以“群”的方式出现，传统单目标处理方法很难奏效。以“群”整体作为处理对象，基于随机有限集(RFS)技术，对“群”的状态特征进行估计。为了解决漏检目标密度分配问题和轨迹关联问题，提出一种面向量测的改进集势概率假设密度(CPHD)滤波器，并结合滤波后的信息处理过程，完成了对低轨空间碎片群的目标密度分布、群内目标数以及群内显著目标的状态估计。在仿真实验中，提出的滤波器表现明显优于传统滤波器和标准CPHD滤波器，且在某些传统滤波器和标准CPHD滤波器已失效的情况下，所提技术仍能有效工作。

空间碎片；群目标；状态估计；随机有限集；改进CPHD滤波器

随着空间碎片数量的不断增加，对空间活动安全造成严重威胁，对空间碎片的监测就显得尤为重要。但是空间碎片数量大、尺寸小导致监测困难，尤其是由于解体或碰撞产生的高密度空间碎片集群成为空间监测和编目的难点[1-2]。例如2007年1月风云1C卫星产生之后6个月已编目的碎片数量达到了1 967个[3]，2009年2月俄罗斯废弃卫星Cosmos2251和美国商业卫星Iridium33碰撞10个月后产生的已编目空间碎片数量达到1 632个[4]。空间碎片在刚产生之后的短时间里相距很近，形成了高密度的空间碎片“云”，且这些碎片中的绝大部分尺寸较小，观测困难。这时候，地基雷达系统由于检测概率低，目标密集无法分辨，以及目标数量大且未知等因素导致无法对空间碎片进行有效监测和编目。

面对这种集群目标，传统方式是先试图估计每个目标的状态，然后才对目标群的状态有个认识。因为传统的多目标滤波算法是先对量测和目标进行关联，然后使用单目标滤波器对每个目标的状态进行估计。最常用的两种方法是多假设跟踪(Multiple Hypothesis Tracking，MHT)滤波器[5]和联合概率数据关联(Joint Probabilistic Data Association，JPDA)滤波器[6]。它们在面对大量密集目标且目标数未知的情况时，滤波表现会大大下降，因为目标关联过程会变得复杂且不稳定，尤其当检测概率较低时。而且这两种传统滤波器无法对区域中的目标数进行估计，只有通过航迹起始和航迹终止过程，依据维持的航迹数来判断目标数，但是航迹起始和终止过程由于检测概率低变得不稳定。因此，在面对这种密集空间碎片群的时候，相比对各目标单独处理，一种有效的策略就是对目标“群”进行整体处理[7]。先对整个空间碎片群的状态进行估计，在信息积累足够或是目标逐渐分开之后再对单个目标的运动状态进行估计，这样即避免了单个目标处理的困难，又能够有效维持对空间碎片的监测。“群监测”的过程中，群特征可以用来对群进行标识和区分，群特征包括群几何(群大小、结构等)、群内目标数量等。如果无法对群中所有目标状态进行估计，可以选择群中检测概率较高目标(本文称之为显著目标)的状态进行估计，用显著目标运动状态来描述群的运动状态。因为群内目标运动状态具有相似性，以群内显著目标运动状态代表群运动状态是合理的。

面对这种需求，在传统方法失效的情况下，随机有限集(Random Finite Set，RFS)理论提供了一个解决集群目标滤波的有效工具。基于RFS理论的多目标贝叶斯滤波器(Multi-target Bayes Filter)是一种将数据关联、目标数估计和状态估计统一在一个概率框架下的多目标滤波算法[8]。在很多近期的研究成果中，多目标贝叶斯滤波器已被应用到了空间目标滤波之中[9-10]。因为最佳多目标贝叶斯滤波器的计算复杂度太高，且很多情况下无法实现，因此有很多基于特定随机过程假设的近似多目标贝叶斯滤波器被提出[11]。其中，基于矩近似的概率假设密度(Probability Hypothesis Density，PHD)滤波器[12]和集势概率假设密度(Cardinalized PHD，CPHD)滤波器[13]具有简洁的公式和低的计算复杂度，可以满足对密集空间碎片实时处理需求。不同于MHT和JPDA滤波器，PHD和CPHD滤波器不是直接估计目标状态，而是对目标密度分布进行估计，密度高的地方认为目标出现概率大，密度低的地方则出现概率小。通过对目标密度分布的估计可以获得群结构特征，即群内目标分布情况和群的范围大小[14]。而目标密度的积分即目标数估计，因此通过对群区域内的PHD进行积分可获得群目标数的估计。但是基于一阶矩近似的PHD滤波器的目标数估计十分不稳定，且无法正确计算漏检目标的PHD[15]，因此传递部分二阶矩的CPHD滤波器被提出。CPHD滤波器在滤波过程中传递目标密度分布的同时还传递目标数的估计函数，因此可以获得稳定的目标数估计。但是CPHD滤波器仍存在一些问题，比如CPHD滤波器虽然可以正确计算漏检目标的PHD，但是无法将其分配到正确航迹上[16]，且CPHD滤波器不继承目标标记，在提取群内显著目标状态上出现困难。已经提出了一些方法使CPHD滤波器具有航迹关联能力[17-18]。本文选择CPHD滤波器对空间碎片群进行滤波，并提出一种新的改进CPHD滤波器，新滤波器中的PHD以量测进行聚合并以此完成数据关联过程，不引入其他关联算法，同时解决了漏检目标的PHD分配问题。完成数据关联后，通过对提取出的空间目标轨迹的检测概率进行估计，取检测概率最大的目标作为群显著目标，从而完成对群显著目标的运动状态估计。

在仿真实验中，改进的CPHD滤波器在不同的观测条件下与JPDA滤波器进行比较，展现了改进CPHD滤波器的在目标状态和目标数估计上的优良性能。在检测概率很低的情况下，JPDA滤波器已经失效，而改进CPHD滤波器仍能有效工作。本文提出的方法为空间碎片群的监测和编目提供了一种新的有效方法。

本文结构如下：第1节对低轨空间碎片群进行描述；第2节介绍了空间碎片群的随机有限集描述；第3节提出改进的CPHD滤波器;第4节对滤波结果进行数据处理过程；第5节通过仿真实验验证方法的有效性；第6节给出本文结论。

1 空间碎片群描述

1.1 空间碎片运动模型

xk=Fk(xk-1)+Qk

(1)

式中：Fk(·)为非线性的动态模型；Qk为模型噪声。

由于空间目标在太空中的受力非常复杂，因此空间碎片的动态模型是非常复杂的非线性模型[19]。本文的动态模型考虑低轨空间碎片的受力包括：①n体运动,将碎片目标、地球、太阳和月亮作为质点处理，空间目标与各质点之间由于万有引力构成一个n体受力系统。② 地球非球形摄动,由于地球的密度分布不均匀，其形状也不是标准球形，而是相当不规则的，其形状和密度分布的非球形部分产生了对空间目标的摄动源。这里考虑10×10阶的非球形摄动位函数。③ 大气阻力,在大气层中飞行的空间目标受到大气阻力的影响。大气阻力主要影响低轨目标，对于高轨目标的大气阻力可以忽略，影响大气阻力的因素有大气密度，碎片与大气的相对运动速度，目标的阻力系数和面质比。④ 太阳光压,太阳光线照在碎片目标上会产生辐射压，太阳光压与碎片目标材料的反射系数以及碎片目标面向太阳的面质比有关。

1.2 典型空间碎片群特征

本文关注的空间碎片群指的是低轨空间突发产生的大量密集空间碎片组成的集群。这里以风云1C空间碎片群为例，对空间碎片群的特征进行描述。取6个密集分布的风云1C碎片目标组成的集群为研究目标，研究数据采用北美空间防空司令部(NORAD)公布的双行根数(Two-Line Element，TLE)，这6个目标的卫星NORAD编号为29727～29732。双行根数是公开数据，这6个碎片最早公布的TLE数据时间是2007年1月18日，而碎片产生的时间是2007年1月11日。为了获得碎片产生之后不久的数据，使用NORAD 专门针对TLE数据开发的轨道传播模型——SGP4模型进行回溯[20]，回溯至2007年1月11日中午，产生一段碎片群运动弧段如图1所示。此弧段具体运动时间从2007年1月11日12:05:46到12:08:38。这6个碎片的平均轨道根数数据如表1所示。使用轨道模型回溯的结果近似真实情况，通过这个近似结果对碎片群进行研究，考虑采用下述特征对空间碎片群进行描述。

图1 风云1C碎片群的一段短弧段Fig.1 A short arc of FENGYUN 1C debris group

表1 风云1C碎片群参数Table 1 Parameters of FENGYUN 1C debris group

NORADIDSemi⁃majoraxis/kmEccentricityInclination/(°)297277022．560．03098．83297287023．720．03199．18297297024．550．02998．93297307025．640．03098．88297317025．930．03098．93297327025．660．03198．89

1.2.1 群几何结构

由图1可以看出，空间碎片群中目标分布密集，相互之间可能由于间距很近而产生遮挡或是无法分辨。但是在运动的这段时间里，6个空间碎片在运动过程中保持了一个相对稳定的位置关系。这是因为密集分布的空间碎片群的轨道模型具有相似性，在短时间内碎片群内目标的运动状态相似，空间碎片群的整体结构较为稳定。

1.2.2 群内目标数

群中目标的数量也是群的一个重要特征。由于群中目标的检测概率并不相同，尺寸大的目标可能比尺寸小的目标检测概率高，且检测概率与目标材质、目标翻滚、目标姿态等因素有关。当群内目标检测概率普遍较低时，要获得准确的群目标数估计比较困难。

1.2.3 群内显著目标

上面已经提到群内目标的检测概率有区别，而空间碎片大多尺寸较小，群内可能大部分目标的检测概率都较低，想要估计各个目标的状态比较困难。为了对群运动状态进行描述，可以通过群内检测概率较高的目标运动状态进行描述，这里将其称为群内显著目标。通过群内显著目标的状态来对群进行标识。从表1中可以看到，群内目标的轨道根数十分相近，即群内目标运动状态相似，通过一个容易估计的显著目标的运动状态来代表一个群的状态是合理的。

1.3 空间碎片群状态估计方法

在前面叙述中已经提到一种可行的解决方案是先尝试对群整体进行滤波，然后在信息足够的情况下再对单个目标进行处理。

群几何可以通过群内目标的分布进行描述。基于RFS理论的CPHD滤波器在滤波过程中传递整个场景的目标密度分布，通过目标密度可以方便地显示群的结构特征。由于检测概率低等因素可能导致估计不准确，但是空间碎片群运动具有稳定性，通过一段时间的信息积累可以获得群几何特征。

在对群内目标数的估计上面，传统方法没有集成目标数估计功能，只有认为存在的轨迹数即目标数，由于不稳定的轨迹起始和轨迹终止过程，目标数的估计结果不稳定。CPHD滤波器在滤波过程中传递的目标数分布，可以容易地对目标数进行估计。

最后是对群内显著目标的运动状态进行估计。CPHD滤波器没有显式集成数据关联过程，因此无法提取显著目标的轨迹。但是由于显著目标检测概率最大，因此其所在位置的目标密度会相对持续地维持较高状态，可以以此从整个群的目标密度分布中提取显著目标状态，但需要对滤波器进行改进。通过对各量测更新的目标密度进行标记，然后关注检测概率高的部分，最后取检测概率最高的目标状态作为群显著目标状态。

空间碎片群状态估计过程框图如图2所示，包含了滤波和数据处理两个流程，其中的详细过程将在后面介绍。

图2 碎片群状态估计过程框图Fig.2 Block diagram of debris group state estimation

2 空间碎片群的随机有限集表示

2.1 空间碎片群的多目标贝叶斯滤波

在低轨空间碎片群的滤波过程中，因为群内目标数未知，观测到的量测数也是未知的，因此将空间碎片群内目标状态和量测建模成随机集形式。在时刻k,碎片群目标状态集合和量测集合分别建模成随机有限集Xk={x1,x2,…,xnk}和Zk={z1,z2,…,zmk},xi和zi分别为单目标状态和单个量测状态。空间碎片群多目标贝叶斯滤波的预测和更新过程[8]为

(2)

(3)

式中：fk|k-1(Xk)和fk(Xk)分别为多目标先验和后验密度；fk|k-1(Xk|·)为多目标状态转移函数；g(Zk|·)为多目标似然函数。积分过程是集积分，定义为

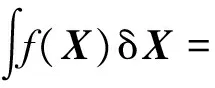
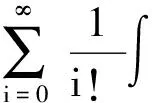
(4)

式中：f({x1,x2,…,xi})为多目标分布函数。其中其遍历分布fn(x1,x2,…,xn)的n!全排列fn(x1,x2,…,xn)的表达式为

f({x1,x2,…,xi})=

(5)

式中：ρ(n)为势(即目标数)分布函数；θ表示一个排列，θ的和即遍历函数的n!个全排列。

2.2 CPHD滤波器

由于集积分在很多条件下无法实现，可以通过对后验多目标分布进行假设，使得集积分形式简化。CPHD滤波器基于独立同分布群过程假设，在滤波过程中传递PHD和势分布函数，可以获得稳定的势估计结果。但是CPHD滤波器仍存在一些缺陷，且碎片群状态估计有其特定要求，因此需要对CPHD滤波器进行改进。下面给出CPHD滤波过程。存活概率和检测概率分别用pS(·)和pD(·)表示，泊松杂波密度函数为κ(·)。详细的CPHD滤波器推导过程见文献[13，21]。

预测假设时刻k-1多目标后验的PHD为vk-1(x)。预测的多目标PHDvk|k-1(x)由存活多目标PHDvS,k|k-1(x)和新生多目标PHDvB,k(x)组成：

vk|k-1(x)=vS,k|k-1(x)+vB,k(x)

(6)

vS,k|k-1(x)=〈pS(·)f(x|·),vk-1(·)〉

(7)

预测的势分布ρk|k-1(n)为

ρk|k-1(n)=

(8)

更新如果多目标先验PHD形式为vk|k-1(x),则多目标后验PHDvk(x|Z)和更新势分布分别为

(9)

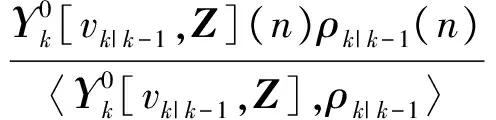
(10)

式中：

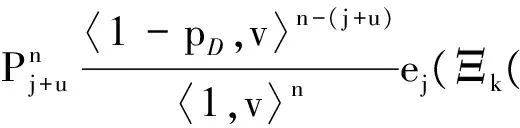
(11)

Ξk(φ,Z)={〈φz(·),1〉:z∈Z}

(12)

(13)

(14)

并规定e0(Z)=1。

遗留PHD，即漏检目标的PHD为

vL,k(x)=

(15)

可以看出，CPHD滤波过程不需要显式的数据关联过程，将整个空间碎片群作为整体处理，假设空间碎片群满足独立同分布过程。正是因为这种不加区分的处理，在CPHD滤波器计算出漏检目标PHD后直接将其分配到整个场景。如式(15)所示，式(15)中计算的漏检目标PHD直接分配到整个场景的预测PHDvk|k-1(x)上。因此，漏检的PHD减少，导致当连续漏检时，可能出现目标丢失。由于空间碎片尺寸小，检测概率低，漏检在空间碎片群滤波时将会十分常见，这个问题必须解决。同时，由于不区分各个目标，无法提取目标轨迹。但是为了估计群显著目标状态，需要提取显著目标轨迹。根据这些实际需求，本文提出改进的CPHD滤波器。

3 面向量测的改进CPHD滤波器

3.1 按量测聚合的目标密度分布

在CPHD滤波器中，每个量测是通过所有轨迹进行联合更新[8]，滤波过程可以认为是面向轨迹的滤波过程。将滤波过程中的PHD成分按量测进行聚合，并用一个二元组进行标记。二元组标识设为c=(k,m),k为量测出现的时间,m为此量测区别于该时刻其他量测的序号。在滤波器更新之后，按同一个量测标记的PHD成分，即标记相同c的PHD成分被认为属于同一个轨迹，通过这样的方式使得PHD成分被区分开来。PHD也由原来的v(x)扩展为v(x,c)。

3.2 面向量测的关联过程

对某一区域PHD的积分是对该区域目标数的估计，这里使用权重w来表述对某PHD成分的积分，即w=〈v(·),1〉。令wi,j表示从轨迹ci到量测zi∈Zk的权重贡献，通过式(16)计算:

wi,jw(ci;zj)=〈v(·,ci;zj),1〉

(16)

量测更新权重由式(17)计算:

(17)

轨迹更新权重则由式(18)计算:

(18)

在获得了权重贡献矩阵之后，大部分的权重可能会集中在矩阵中的部分位置，而有许多位置的权重值可能小到可以忽略。因此，通过下面的过程可以对矩阵进行简化，通过这种简化也可减少后面的数据关联过程产生的关联结果。

上一时刻的轨迹通过权重贡献和该时刻观测到的量测进行关联。权重贡献越大，说明量测与轨迹之间关联的可能性越大，反之亦然。当权重贡献大于一个预先设定的阈值T1时，认为该量测来自该轨迹，其他关联就不再考虑；反之，当权重贡献小于一个预先设定的阈值T2时，认为该量测必定不是来自该轨迹，权重贡献设置为0。然后，所有的关联结果都保留下来，形成多条可能轨迹。但是其中关联到同一个量测的轨迹是互斥轨迹，即这两条轨迹不可能同时存在，互斥轨迹在最后的结果中只能保留一条。

3.3 漏检目标的PHD处理

在CPHD滤波器中，遗留PHD的分配结果不正确。在通过上述对PHD成分进行标记之后，可以通过标记对遗留PHD进行正确分配。

先考虑一个单独轨迹。一条轨迹的消失权重wD(c)加上漏检权重wL(c),再加上存活权重(即检测更新权重)wU(c),等于1，即wD(c)+wL(c)+wU(c)=1。设该轨迹的预测权重为wk|k-1(c),则预测的消失权重为1-wk|k-1(τ)。设一个常数的检测概率为pD,则该目标漏检的权重为存活权重wk|k-1(c)与漏检概率1-pD的乘积，即(1-pD)wk|k-1(c)。

因此，在该目标未检测到的情况下，目标消失和目标漏检权重的比值满足：

(19)

则漏检权重可以表示为

(20)

而轨迹的概率分布可以通过式(21)计算:

(21)

整个场景中遗留PHD的积分就是漏检目标数估计NL,k=〈vL,k(·),1〉。则最终通过将NL,k按各轨迹漏检权重进行按比例分配，得到修正后的各轨迹的遗留PHD，计算公式为

(22)

3.4 新出现碎片模型

通过这样的模型，来自两个时刻的所有量测都可以建模为新生目标状态，但是其中只有少量相距较近的两个量测建立的新生目标状态是合理的。这里通过轨道能量模型进行约束，剔除不合理的新生目标状态。

先假设碎片轨道是圆轨道，因为一般碎片运动的轨道偏心率都很小。则速度大小可以通过式(23)计算:

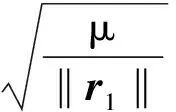
(23)

式中：μ为引力常数和地球质量的乘积。在考虑了量测误差的情况下，如果初始的速度大小‖v1‖大于两倍的‖v*‖,就认为此速度是不合理的，这个新生目标状态被剔除。

同时，一个量测如果来自已存在目标，则不是新目标。因此量测来自新目标的概率与其更新权重w(z)成反比，此概率写为1-w(z)。还可以设定一个阈值，如果小于阈值则该量测不进行新目标起始。

3.5 状态估计过程

4 群状态估计数据处理过程

在完成了实时的空间碎片群滤波之后，需要对滤波后的数据进行处理，从中获取所需要的群状态信息。

4.1 轨迹提取

在改进的CPHD滤波过程中，面向量测的聚合PHD过程使得各个时刻的量测可以关联起来。在滤波结束之后，可以尝试从各时刻滤波结果中提取各空间碎片的轨迹。当检测概率很低时，可能只有部分目标能提取轨迹，比如显著目标，通过提取的显著目标轨迹可以对其进行状态估计和定轨，用来描述整个碎片群状态。

在碎片目标分布十分密集的情况下，关联结果会出现多种可能，最后产生多条轨迹。这里将每条可能轨迹的所有权重贡献的乘积作为轨迹的权重，如出现漏检则乘以漏检权重wL(c)。最后，取某碎片的多条轨迹中权重最大的轨迹作为碎片轨迹。其中如果存在互斥轨迹，则互斥轨迹中选择权重最大的轨迹，其他轨迹舍弃。轨迹长度须满足一定的连续时间步长，而轨迹数可能小于目标数估计。

4.2 显著目标状态估计

由于检测概率低等因素导致提取的轨迹数可能小于目标数估计，在这种情况下，对检测概率较高的目标进行状态估计的结果会相对稳定。因此，提取检测概率较高目标的状态估计结果作为群显著目标状态。

在进行了面向量测的关联过程之后，可以从滤波结果中提取轨迹。提取的航迹长度不能太短，太短没有实际意义。可以根据实际情况设定长度阈值，大于阈值的航迹才有参考价值。航迹检测概率可以通过式(24)进行计算:

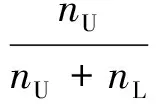
(24)

式中：nU为检测更新次数；nL为漏检次数。

然后取其中检测概率最高的目标作为群的显著目标，通过其轨迹可以对其进行状态估计和定轨，结果作为群的一个特征。在对空间碎片群进行识别的过程中，显著目标的状态(如轨道根数)就可以作为一个识别群的依据。

5 仿真实验

本文提出的改进CPHD滤波器使用高斯混合(Gaussian Mixture，GM)实现[22]，由于目标运动模型是复杂的非线性模型，使用不敏卡尔曼滤波器(Unscented Kalman Filter，UKF)进行滤波[23]。同时使用经典CPHD滤波器和JPDA滤波器作为比较。在仿真实验中，考虑一个包含4个碎片的低轨空间碎片群目标，设这4个目标是在2007年1月11日07:00:00产生。刚产生时的轨道根数数据见表2，其中显著目标是目标1。碎片的运动模型已经在1.1节中介绍，而量测模型为

zk=Hk(x)+Rk

(25)

式中：Rk为量测误差；Hk(·)为非线性的量测方程。雷达可观测到目标相对雷达站址的方位角、俯仰角和距离。雷达的站址设为

rR=[-1 787.37 5 500.97 2 679.10] km

雷达的观测区域为方位角75°～105°、俯仰角0°～90°范围。在一天时间里，空间碎片群两次经过雷达观测区域，此过程示意见图3。图3表示雷达在先观测到一次碎片群后，随地球自转再次观测到碎片群的过程。第1次碎片群通过雷达观测区域的时间为8:43:04到8:44:05，第2次通过雷达观测区域的时间为20:36:47到 20:39:32。

采样间隔设置为1 s。雷达的量测误差考虑[0.1° 0.1° 50 m]和[0.2° 0.2° 100 m]两种情况，而每次量测的平均杂波数取nC=10或nC=50。杂波平均分布区域为

V=[0.4π 0.6π]rad×[0.05π 0.25π]rad×[300 2 300] km

因此平均杂波密度为λC=1.37×10-2(rad2·km)-1或λC=6.85×10-2(rad2·km)-1。检测概率考虑3种情况，除显著目标外的其他目标的检测概率取pD=0.3，0.6，0.9,显著目标检测概率则分别取pD=0.5,0.8，0.95。目标的存活概率为pS=0.99。CPHD和改进CPHD滤波需要通过修剪和合并过程减少高斯混合分量数，修剪的阈值为Tp=10-4,合并的阈值为Tm=4,且规定高斯分量数不能超过100个。新生目标权重取0.05。另外，改进CPHD滤波过程中的两个阈值分别取T1=0.9和T2=10-4。由于目标检测概率不同，而滤波器只能设置固定的检测概率，改进CPHD对目标数估计可能出现不稳定，这里对每个更新量测权重设置必须满足w(z)>0.3才进行状态估计。

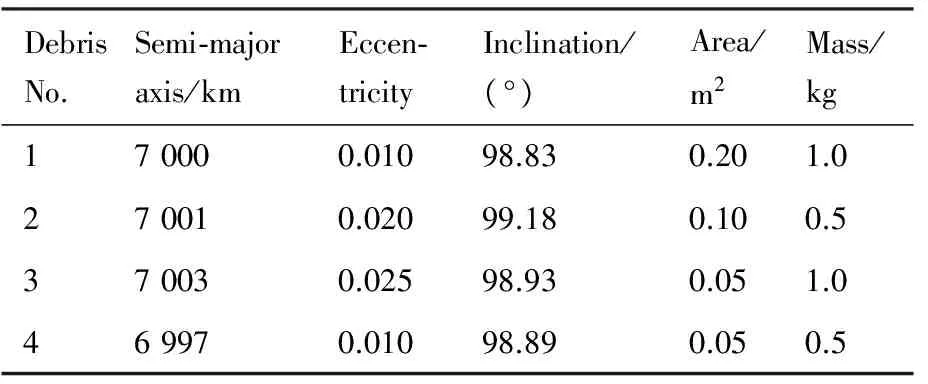
表2 仿真实验碎片群参数Table 2 Parameters of simulated debris group

图3 碎片群的两段观测弧段(红色)和两次观测的 雷达位置(黑点)示意图 Fig.3 Sketch of two observed arcs of debris group (red line) and two observing position of radar (black dot)

此外，在JPDA滤波器中使用与CPHD和改进CPHD滤波器相似的面向量测的轨迹起始过程，连续关联两次就起始一条轨迹；如果一条轨迹连续3次在确认门限中没有量测关联则终止此轨迹。JPDA的目标数估计就是存活的轨迹数。

在改变观测条件进行仿真时，通过200次蒙特卡罗仿真实验的平均结果来检验改进的CPHD滤波器的性能，每次蒙特卡罗实验中碎片的轨道不变，随机产生空间碎片的量测数据。图4～图9分别显示了改进CPHD滤波器对群几何、群内目标数和群内显著目标状态估计的结果。随着检测概率降低，量测误差增大，以及杂波密度上升，改进的CPHD滤波器表现有所下降，但是都能有效估计出群内目标分布、目标数，并提取出显著目标状态。证实了在观测条件比较恶劣的情况下，所提方法对空间碎片群运动状态估计取得较好的效果。而且，在相同条件下，CPHD滤波器和JPDA滤波器也进行了仿真，通过比较来观察改进CPHD的效果。下面详细介绍各仿真实验结果。

在对群几何结构的估计中， 使用最优子模式分配(Optimal Sub-Pattern Assignment，OSPA)[24]距离来评估其估计结果。OSPA距离是用来评价估计结果的，它在考虑目标分布准确性的同时，也考虑了目标数估计的准确性，是合理的误差距离准则。200次蒙特卡罗实验的平均OSPA距离如图4和图5所示。

图4 弧段1的200次蒙特卡罗平均OSPA距离Fig.4 Mean OSPA distance over 200 Monte Carlo runs of the first arc

图5 弧段2的200次蒙特卡罗平均OSPA距离Fig.5 Mean OSPA distance over 200 Monte Carlo runs of the second arc

从图4和图5中可以看出，观测条件越恶劣，CPHD滤波器、改进CPHD滤波器和JPDA滤波器的滤波表现越差，但是总体上改进CPHD滤波器的表现都比CPHD和JPDA滤波器好很多，说明改进CPHD滤波器对群内目标分布估计的精度和稳定性比CPHD和JPDA滤波器好。在检测概率为0.9的情况下，3个滤波器都能比较好地工作。在检测概率降低到0.6时，3个滤波器的表现都出现大幅度下降。由于CPHD滤波器无法正确分配漏检目标的PHD，CPHD滤波器表现下降很快。当检测概率进一步降低到0.3时，CPHD和JPDA滤波器已经无法工作，而改进CPHD滤波器仍能工作，展示了改进CPHD滤波器的稳定表现，也证实了其对漏检目标PHD的正确处理。

图6 弧段1的200次蒙特卡罗目标数估计Fig.6 Mean cardinality estimate over 200 Monte Carlo runs of the first arc

图7 弧段2的200次蒙特卡罗目标数估计Fig.7 Mean cardinality estimate over 200 Monte Carlo runs of the second arc

200次蒙特卡罗实验的平均目标数估计如图6和图7所示，其中不同颜色虚线为对应的平均估计标准差范围，两种滤波器在观测条件不断恶化的时候标准差都在不断增大，即估计结果变得不稳定。从图6和图7中可以看出，3个滤波器在检测概率为0.9时能估计出群中包含了4个目标，其中CPHD在弧段2后半段出现估计偏差。当量测误差增大时，CPHD和JPDA滤波器的表现有所下降。当检测概率降低到0.6时，CPHD和JPDA滤波器对目标数的估计出现偏差，已经无法准确估计目标数，而改进CPHD滤波器仍能估计出4个目标；当检测概率降低到0.3时，JPDA滤波器的估计已经无效，CPHD滤波器的表现优于JPDA滤波器，但也无法准确估计目标数，而改进CPHD滤波器仍能在一段时间后估计出有4个目标，说明其在检测概率很低的情况下仍能工作，只是估计结果的标准差(起伏)变大。

图8 弧段1的200次蒙特卡罗群显著目标估计 均方根误差Fig.8 RMSE of conspicuous debris object over 200 Monte Carlo runs of the first arc

图9 弧段2的200次蒙特卡罗群显著目标估计 均方根误差(改进CPHD)Fig.9 RMSE of conspicuous debris object over 200 Monte Carlo runs of the second arc (improved CPHD)

200次蒙特卡罗实验对群显著目标估计的均方根误差(RMSE)如图8和图9所示。从图8和图9中可以看出，随着量测误差的增大，对显著目标RMSE的估计也越来越大；而检测概率越低，RMSE误差减小得越慢，且估计精度也缺差。但是，即使是在检测概率很低的情况下，改进CPHD滤波器仍能估计出较为准确的结果，可以对群内的显著目标状态给出较为准确的估计，从而通过显著目标状态来了解群状态就更加可信，也可以通过此状态来对群进行标识和分辨。

6 结 论

1) 在对面空间碎片群时，由于低检测概率、群内目标密集分布且目标数未知，传统单目标处理方法已经无法有效工作。

2) 改进的CPHD滤波器解决了漏检目标PHD分配问题，且集成轨迹标识过程，使其可以提取群内显著目标状态。

3) 仿真实验通过多种不同的观测条件，验证了本文提出的方法是一种对空间碎片群运动状态估计的有效方法。

因为实际的空间碎片群观测更加复杂，未来的工作需要将滤波过程推广到检测概率未知的条件下去，同时通过定轨和轨道改进等方式对空间碎片群以及群内目标不同弧段的观测进行弧段关联。

[1] 刘静, 王荣兰, 张宏博, 等. 空间碎片碰撞预警研究[J]. 空间科学学报, 2004, 24(6): 462-469.

LIU J, WANG R L, ZHANG H B, et al. Space debris collision prediction research[J]. Chinese Journal of Space Science, 2004, 24(6): 462-469 (in Chinese).

[2] 李春来, 欧阳自远, 都亨. 空间碎片与空间环境[J]. 第四纪研究, 2002, 22(6): 540-551.

LI C L, OUYANG Z Y, DU H. Space debris and space environment[J]. Quaternary Sciences, 2002, 22(6): 540-551 (in Chinese).

[3] JOHNSON N L, STANSBERY E, LIOU J C, et al. The characteristics and consequences of the break-up of the Fengyun-1C spacecraft[J]. Acta Astronautica, 2008, 63(1-4): 128-135.

[4] PARDINI C, ANSELMO L. Physical properties and long-term evolution of the debris clouds produced by two catastrophic collisions in Earth orbit[J]. Advances in Space Research, 2011, 48(3): 557-569.

[5] BLACKMAN S S. Multiple hypothesis tracking for multiple target tracking[J]. IEEE Aerospace & Electronic Systems Magazine, 2004, 19(1): 5-18.

[6] FORTMANN T E, BAR-SHALOM Y, SCHEFFE M. Sonar tracking of multiple targets using joint probabilistic data association[J]. IEEE Journal of Oceanic Engineering, 1983,8(3): 173-184.

[7] HUANG J, HU W D. MCMC-particle-based group tracking of space objects within Bayesian framework[J]. Advances in Space Research, 2014, 53(2): 280-294.

[8] MAHLER R P S. Statistical multisource-multitarget information fusion[M]. Norwood, MA: Artech House, 2007: 305-538.

[9] WEI B, NENER B, LIU W. Tracking of space debris via CPHD and consensus[C]∥International Conference on Control, Automation and Information Sciences, 2015: 436-441.

[10] JONES B A, VO B N. A labeled multi-Bernoulli filter for space object tracking[C]∥AAS/AIAA Space Flight Mechanics Meeting, 2014.

[11] MAHLER R P S. Advances in statistical multisource-multitarget information fusion[M]. Norwood, MA: Artech House, 2014: 181-215,379-403

[12] MAHLER R P S. Multitarget Bayes filtering via first-order multitarget moments[J]. IEEE Transactions on Aerospace & Electronic Systems, 2003, 39(4): 1152-1178.

[13] MAHLER R. PHD filters of higher order in target number[J]. IEEE Transactions on Aerospace & Electronic Systems, 2007, 43(4): 1523-1543.

[14] MAHLER R P S, ZAJIC T. Bulk multitarget tracking using a first-order multitarget moment filter[J]. Proceedings of SPIE-The International Society for Optical Engineering, 2002, 4729: 175-186.

[15] ERDINC O, WILLETT P, BAR-SHALOM Y. Probability hypothesis density filter for multitarget multisensor tracking[C]∥International Conference on Information Fusion, 2005: 1-8.

[16] FRANKEN D, SCHMIDT M, ULMKE M. “Spooky action at a distance” in the cardinalized probability hypothesis density filter[J]. IEEE Transactions on Aerospace & Electronic Systems, 2009, 45(4): 1657-1664.

[17] PANTA K, CLARK D E, VO B N. Data association and track management for the gaussian mixture probability hypothesis density filter[J]. IEEE Transactions on Aerospace & Electronic Systems, 2009, 45(3): 1003-1016.

[18] 欧阳成, 姬红兵, 张俊根. 一种改进的CPHD多目标跟踪算法[J]. 电子与信息学报, 2010, 32(9): 2112-2118.

OUYANG C, JI H B, ZHANG J G. Improved CPHD filter for multitarget tracking[J]. Journal of Electronics & Information Technology, 2010, 32(9): 2112-2118 (in Chinese).

[19] 刘林. 航天器轨道理论[M]. 北京： 国防工业出版社, 2000: 99-326.

LIU L. Orbit theory of spacecraft[M]. Beijing: National Defense Industry Press, 2000: 99-326 (in Chinese).

[20] VALLADO D, CRAWFORD P, HUJSAK R, et al. Revisiting spacetrack report #3[C]∥AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Reston, VA: AIAA, 2006: 1-88.

[21] VO B T, VO B N, CANTONI A. Analytic implementations of the cardinalized probability hypothesis density filter[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3553-3567.

[22] VO B N, MA W K. The Gaussian mixture probability hypothesis density filter[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4091-4104.

[23] JULIER S J, UHLMANN J K. Unscented filtering and nonlinear estimation[J]. Proceedings of the IEEE, 2004, 92(3): 401-422.

[24] SCHUHMACHER D, VO B T, VO B N. A Consistent metric for performance evaluation of multi-object filters[J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3447-3457.

Stateestimationofspacedebrisgroupbasedonrandomfiniteset

LUZhejun,HUWeidong*

ATRKeyLab,CollegeofElectronicScienceandEngineering,NationalUniversityofDefenseTechnology,Changsha410073,China

Basedonthesingletargetstateestimation,theconventionalapproachisnotabletoworkwellwhenfacedwithalargenumberofsuddenlygeneratedspacedebrisobjects,asthoseobjectsareclosely-spacedasagroupwithsmallsize.Thus,basedontheRandomFiniteSet(RFS)theory,thespacedebrisgroupistreatedastheprocessingobjectanditsstatesareestimatedinthiswork.Inordertoaddresstheissuesofmissedobjectdensitydistributionandtrajectoryassociation,animprovedmeasurement-orientedCardinalizedProbabilityHypothesisDensity(CPHD)filterisproposed.Withadataprocessingusedafterfiltering,thisfilteraccomplishestheestimationofobjectdensitydistribution,objectnumberandconspicuousobjectstateinagroup.Insimulations,theproposedfiltersignificantlyoutperformstheconventionalfilterandCPHDfilter.Itcanworkinchallengingenvironment,andmeanwhile,theconventionalfilterandCPHDfilterfail.

spacedebris;groupobject;stateestimation;randomfiniteset;improvedCPHDfilter

2017-02-28；Revised2017-03-28；Accepted2017-04-27；Publishedonline2017-04-281648

URL：http://hkxb.buaa.edu.cn/CN/html/20171124.html

NationalNaturalScienceFoundationofChina(61372162)

.E-mailwdhu@nudt.edu.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.321200

V412

A

1000-6893(2017)11-321200-11

2017-02-28；退修日期2017-03-28；录用日期2017-04-27；< class="emphasis_bold">网络出版时间

时间：2017-04-281648

http://hkxb.buaa.edu.cn/CN/html/20171124.html

国家自然科学基金(61372162)

.E-mailwdhu@nudt.edu.cn

卢哲俊， 胡卫东. 基于随机有限集的空间碎片群运动状态估计方法J. 航空学报，2017,38(11):321200.LUJZ,HUWD.StateestimationofspacedebrisgroupbasedonrandomfinitesetJ.ActaAeronauticaetAstronauticaSinica,2017,38(11):321200.

(责任编辑：苏磊)