基于旋转轴向阵列的风扇宽频噪声实验

许坤波，乔渭阳，霍施宇，程颢颐, 仝帆

1.西北工业大学 动力与能源学院，西安 710072 2.航空工业飞机强度研究所 三十二室，西安 710065

基于旋转轴向阵列的风扇宽频噪声实验

许坤波1,*，乔渭阳1，霍施宇2，程颢颐1, 仝帆1

1.西北工业大学 动力与能源学院，西安 710072 2.航空工业飞机强度研究所 三十二室，西安 710065

航空发动机降噪研究迫切需要一种叶轮机械管道内宽频噪声测量方法来指导降噪设计。本文通过对阵列测量的声压信号进行互相关分析，得到管道内顺流和逆流传播的模态声功率结果。安装在风扇实验台进口段的传声器阵列由2排周向间隔180°的轴向阵列组成，每排阵列有14个等间距的传声器。阵列安装在可周向旋转的测量段上，实验中测量段每隔6°旋转一次，共获得840个测点位置的声场信号。结果表明入射波与反射波最大可相差10 dB。模态分解结果表明，转静干涉模态是转子通过频率及其谐频处的主导模态。利用不同参考信号计算出的声场结果相同，说明该实验测试方法对参考信号位置没有特殊要求，进一步说明该方法有很好的适用性。

宽频噪声；模态；阵列；叶轮机械；风扇

商用飞机的噪声问题始终是社会关注的焦点，其中航空发动机噪声在大多数飞行状态下都是其主要的噪声源。航空发动机噪声包括单音噪声(例如转子自噪声，蜂鸣声和转静干涉噪声)和宽频噪声[1]。

随着对容易控制的航空叶轮机单音噪声源和喷流噪声源进行有效控制，湍流宽频噪声逐渐成为发动机主要噪声源，特别是处于湍流流场中高速旋转的叶轮机叶片产生的宽频噪声[2]。对于管道内多个模态的传播特性，Morfey[3-5]、Rice[6-7]、Farassat[8]和Abom[9]等进行了深入的探索。研究表明管道内模态是以螺旋旋转的方式向上下游进行辐射传播，高阶模态的传播特性非常依赖于频率，针对管道模态的截止特性成功地进行了预测和验证。当管道内有均匀气体流动时，单个模态辐射的声功率与无气流时的结果存在一个系数对应关系，这个系数与马赫数相关。当管道内存在气流时，对管道内声压进行准确测量变成了难题，因为传声器接收的压力脉动信息不仅包含声压脉动，还包含湍流压力脉动。Chung[10]基于假设三个不同位置的麦克风测量的湍流压力脉动是互不相关的，通过对测量信号进行互相关来消除湍流压力脉动的干扰，但这种方法仅对声场是完全相关的情况有效。柏林工业大学Michalke教授等[11-13]于20世纪90年代研究了管道内声场的相干特性。当声源是单个质量源单极子时，管道内声压是完全相关的，因而所有模态也是相关的。并提出一种检验管道内声场相关性的方法，指出只有当声场是完全相关的，声压频谱才能通过3个测点处的互谱密度计算出来。

在气流管道内声波信号相干性理论的研究工作基础上，并基于圆柱形气流管道内声波运动方程理论分析解和统计平均概念，德国宇航院(DLR)的Enghardt[14]和Tapken等[15-16]首次提出并证实叶轮机械管道内部的湍流随机宽频噪声仍然是以统计平均的模态波形式传播。在假定不同声模态之间互不相关且湍流宽频噪声平均声场是恒定的前提下，提出了一种宽频噪声声功率评估方法，他们通过将传声器阵列测量信号与管道内固定位置参考信号进行相干分析，获得气流管道内向前和向后传播的模态波幅值信息，进而得到总声功率。针对管道内声模态实验测量，NASA[17]、DLR[18-19]、汉诺威大学[20-21]和佛罗伦萨大学[22]使用了轴向阵列和径向阵列对管道内声场进行了测量，结果表明径向阵列会受到尾迹气流的影响，并且其对加工和安装精度很敏感。轴向阵列虽然可以不受尾迹的影响，但是需要在流动方向布置数圈测点。当频率增大时，所需要安装的传声器总个数呈指数增长，这就使得该方法的实用性大大降低。

本文设计加工了一种新型旋转测量装置，该装置可以让布置于壁面的传声器阵列沿着周向进行旋转测量，从而大大减少了声学测量所需的传声器总个数，并有效地拓宽了声学研究频率范围。为了进一步保证声学测量中的相位稳定性，首次通过单个数字采集器对轴转动信息和声压信号进行同步采集，从而大大增加了数据信噪比。实验中在风扇进口段安装了两排轴向传声器阵列，每排阵列由14个等间距分布的传声器组成，两排阵列周向间隔180°。声学测量中每旋转6°采集一次，实验中旋转半圈共可得到840 个测点位置的声场信息。通过相关分析得到各模态波的幅值频谱，进而求得管道内顺流和逆流传播的声功率频谱。该方法可以用于评估声衬或其他降噪设备的有效性。

1 实验对象和测量设备

1.1 风扇实验台

实验对象是西北工业大学叶轮机械气动力学和气动声学实验室的单级低速轴流风扇实验件NPU-Fan。实验件的设计参数如表1所示。风扇管道内转静干涉模态截通特性如表2所示，表中：BPF(Blade Passing Frequency)为叶片通过频率；m为周向模态数；Nn为谐波数；K为整数；B和V分别为转、静叶片数。

为了更精确地测量管道内声场特性，消除不必要的噪声污染，实验的声学环境尤为重要。本次实验对现有的风扇实验台进行了必要的声学实验条件改善，主要包括：

1) 将风扇进口段、声学测量段放置于飞机强度所(ASRI)的半消声室内部，如图1(a)所示，目的是为了减少和消除外部噪声反射到风扇进口测量段。

2) 增加安装风扇排气吸声管道，如图1(b)所示，目的是为了减少排气段产生的额外噪声，并消除排气噪声向进口管道的辐射。

表1 风扇主要设计参数Table 1 Main design parameters of fan

表2 NPU-Fan转静干涉模态分析

图1 放置于飞机强度研究所半消声室内的NPU-FanFig.1 NPU-Fan in semi-anechoic room of Aircraft Strength Research Institute (ASRI)

1.2 声学测量设备

风扇试验台简图如图2所示。声学测量装置安放在风扇进口段，距转子叶尖前缘1.90 m。实验中采用旋转阵列来对管道声场进行测量，即传声器阵列安装在旋转机匣上(图3(a)所示)。这样做的好处是可以通过安装少量的传声器来获得更多位置处的声压信息。实验中安装了2排轴向阵列，每排阵列由14个等间距分布的传声器组成，轴向间距为2.4 cm，2排阵列周向相隔180°。为了达到周向定角度声学测量的目的，旋转测量段设计成由步进电机驱动，步进电机单次脉冲带动齿轮旋转的角度是固定的。本次实验中周向每旋转6°进行一次测量。实验中在旋转测量段上游20 cm处放置了2个位置固定的传声器，其轴向位置如图2所示。周向位置如图3(b)所示，两者相隔100°。实验中声学信号和红外信号同时由Müeller-BBM PAK Mobile MK-Ⅱ数据采集系统采集，采样频率是16 384 Hz，每个测点采集时间是12 s。

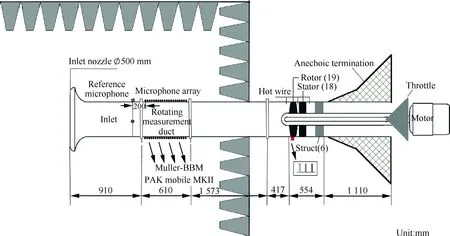
图2 风扇实验台简图Fig.2 Diagram of fan rig

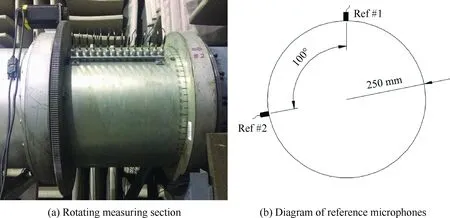
图3 声学测量装置示意图Fig.3 Schematic of noise measurement device

1.3 红外传感器

对于旋转测量，由于各周向测点位置的声场信息不是同时采集，因此各周向测量位置处的声学信号之间的相位差不是恒定的。因此虽然旋转阵列相较于固定阵列优势明显，但其难点是保证各测点处的声压信号相位差稳定。本次实验中为了保证每次测量时对应的转子转动位置相同，实验中在转子前缘的机匣壁面安装了红外传感器(图2所示)，反射胶纸放置于轮毂处。转子单次旋转可测量到单次脉冲信号(如图4所示)。

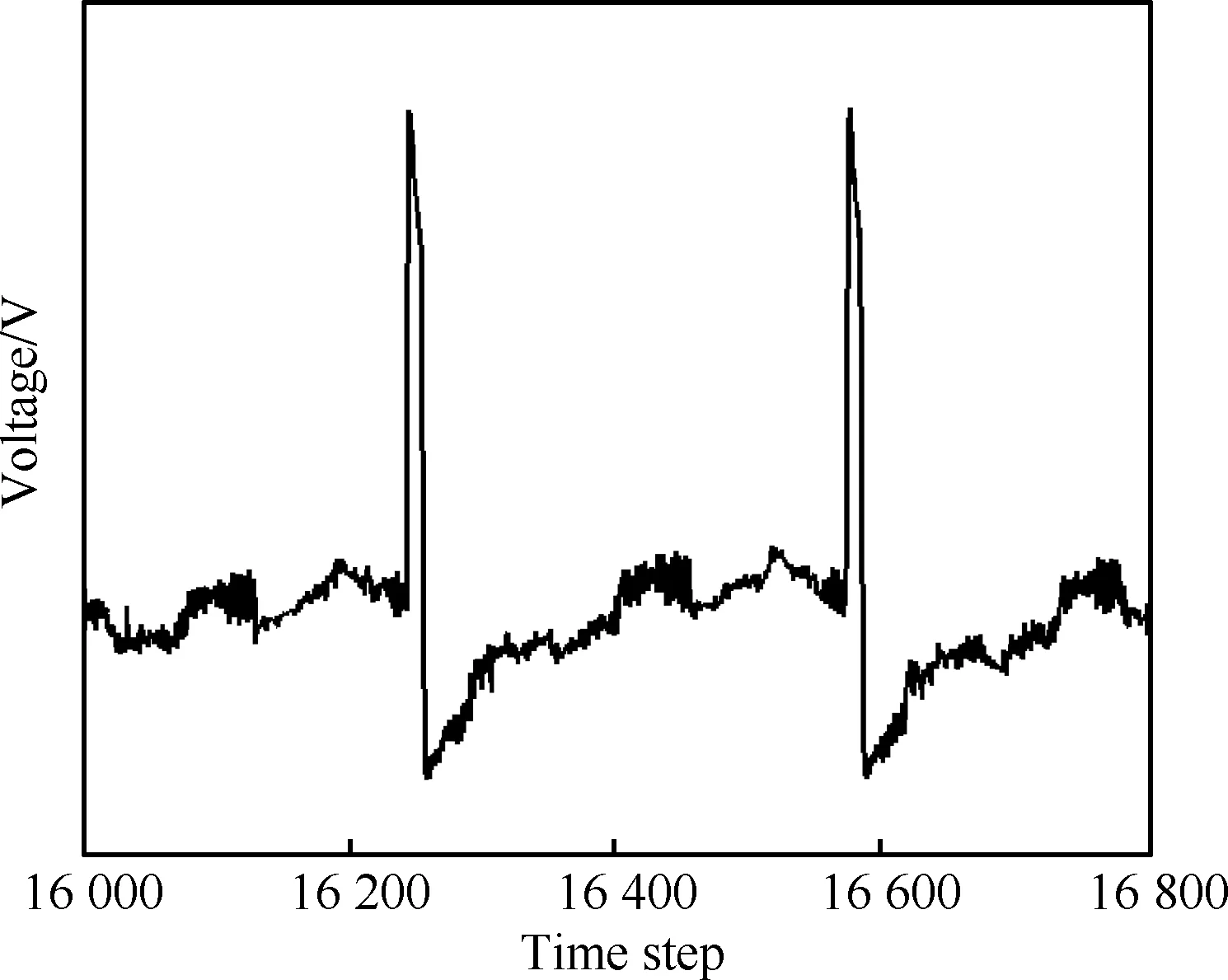
图4 红外传感器采集的脉冲信号Fig.4 Pulse signal acquired by infrared sensor

2 宽频噪声测试方法

2.1 管道声学理论

在以下假定条件下：

1) 不可压缩介质，等熵流动，并且忽略温度梯度；2) 轴向和周向平均速度分布以及管道截面形状在轴向方向保持不变；3) 没有径向速度分布；4) 周向和轴向流速不随时间发生变化；5) 介质的温度和密度在空间和时间上都是不变的。

圆形/环形管道内圆柱坐标系(x,r,φ)下的声学传播方程可以写成

(1)

对于声场在圆柱或环形的硬壁管道内传播，式(1)可以得到一种数值解，对于某个频率可以由模态波的线性叠加得来[1]。

(2)

式中：

(3)

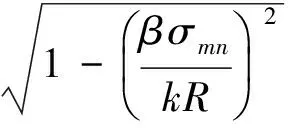
(4)

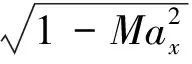
(5)

(6)

(7)

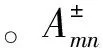
模态截通频率由式(8)可得，可知其与气流马赫数、管道轮毂比、管道参数相关。根据模态幅值可以通过式(9)计算出模态声功率。

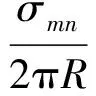
(8)

(9)

2.2 管道宽频噪声测量方法

在叶轮机管道内部的湍流随机宽频噪声仍然是以统计平均的模态形式传播，基于圆柱形气流管道声波传播方程理论分析解和统计平均概念，在假定不同声模态互不相关且湍流宽频噪声平均声场是稳态的前提下，考虑到2个附标为mic和ref的麦克风信号，应用式(2)，则两个位置声压信号的相关结果可以写成模态组合形式，即式(10),式中*为共轭形式。

(10)

式(10)中模态形状函数为

(11)

为了表述方便将任意模态(m,n),(μ,ν)设为i和j，则式(10)中的大括号项变为

(12)

i≠j⟺m≠μ,n≠ν

(13)

式(12)最后两项是不同阶模态之间的交叉项，假设不同模态之间是不相关的，即

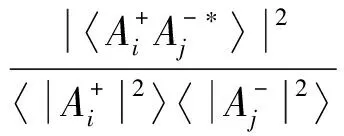
(14)

而且考虑到不同模态之间特征函数的正交特性，这些交叉项变得可以忽略不计，即可以略去式(12)的最后两项，即

(15)

这样每个截通模态会产生4个未知数，为减少未知数数目，可以将模态的轴向波数写为

(16)

式中：C1、C2和kM为中间参数，无实际含义。

这样式(15)的最后两项可以写为

(17)

其中未知数向量可以写成式(18)，最终管道宽频噪声模态分解可以写成式(19)形式。实际实验操作中，通常已知数个数大于未知数个数，而且系数矩阵奇异，在求解这种系数矩阵奇异且方程超定的矩阵时，论文中采用奇异值分解方法[23-24]来进行矩阵求解。

(18)

(19)

3 实验测量结果和分析

根据式(8)，可以计算出各个频率下模态截通函数。如图5所示，实线表示截通的模态总个数，点划线和虚线分别表示截通模态中周向和径向模态的最高阶数。在2 500 Hz时共有38个模态截通，其中周向模态最大阶数为m=±9,径向模态最大阶数为n=3。随着频率增大，截通的模态个数急剧增多，这使得中高频的模态分解变得更难实现。

对于管道内模态分解，在了解模态截通特性后，确定模态分解的频率范围变得很重要。通常模态分解的频率范围由以下几方面决定：

1) 矩阵求解前提是已知数大于等于未知数，因此由式(19)可知，测点个数要大于可截通模态个数的三倍，即Np≥3Nmode。

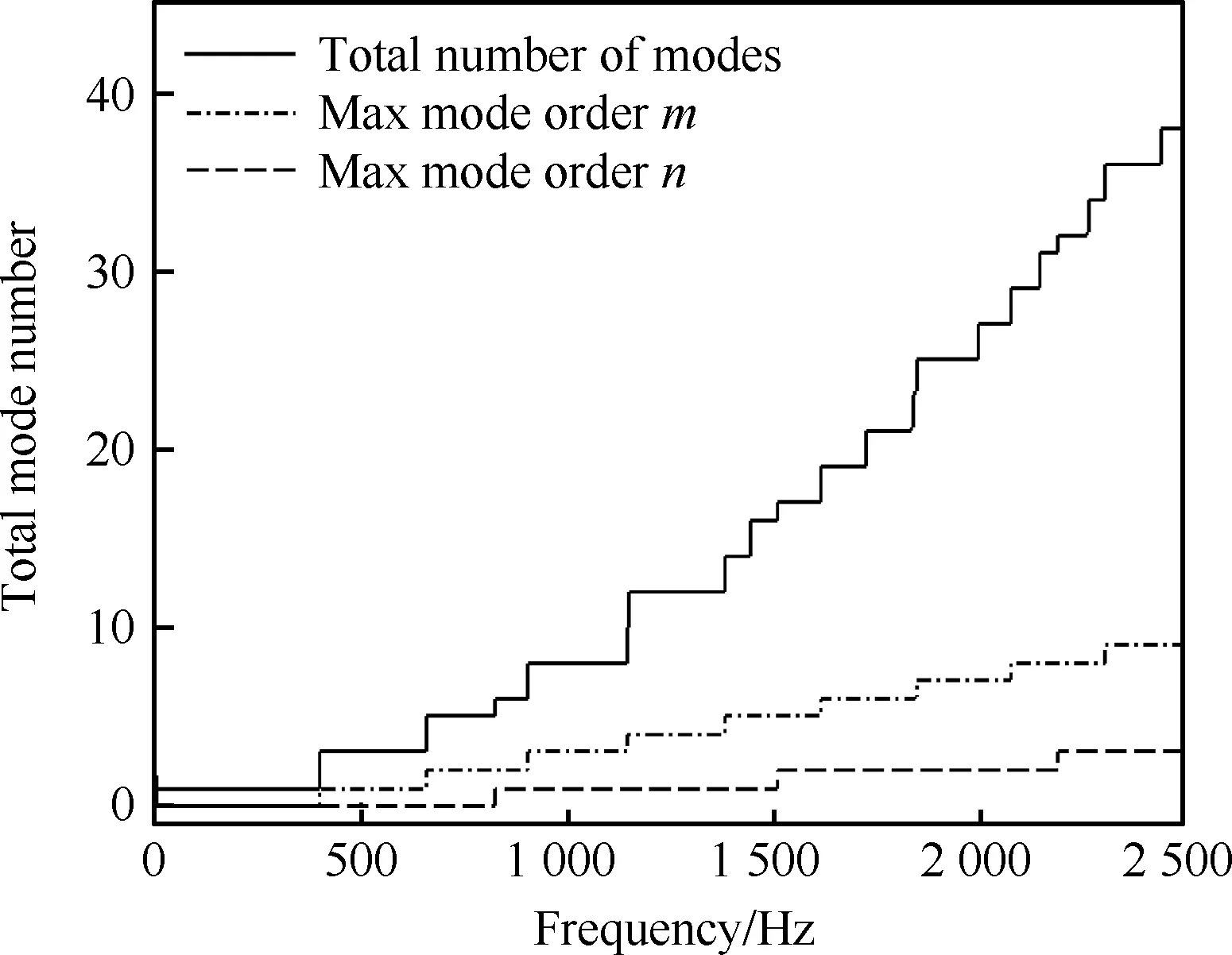
图5 不同频率处模态传播个数Fig.5 Mode wave numbers at various frequencies

2) 由模态分解理论，以及奈奎斯特定理可知，要想准确分解一个波形，必须满足测点数大于等于波个数的两倍，对于周向模态分解，为了不产生混淆，周向测点个数要大于两倍周向模态阶数，即Nθ≥2maxm。

3) 对于径向模态分解，因为采用的是轴向阵列。径向模态分解主要靠的是不同模态的轴向波数不同从而在相同的轴向间距Δx下，不同模态的相位差是不同的 ，一个径向模态至少需要两个轴向位置的声压信息进行分解Nx≥2maxn。

对于真实实验中的模态分解，除了满足上述三项要求以外，还需要考虑到求解误差的因素。因为模态分解中主要通过模态轴向波数不同来分解各个模态，因此计算各个模态的轴向波数(或者是波长)变得很有必要。图6所示是Max=0.1时顺流传播模态的轴向波长，其波长是由轴向波数换算过来的，可以反映各个模态沿轴向的传播特性。随着频率增加，不同模态的波长变得很接近而难以分辨，这会导致中高频的模态更难被分解。

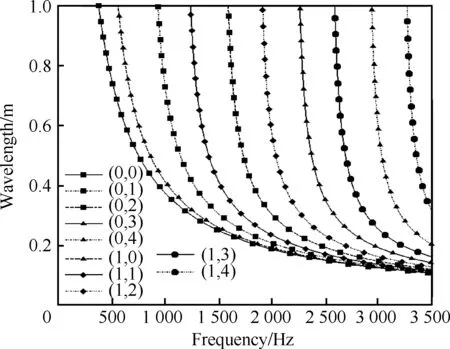
图6 不同模态波的波长Fig.6 Wavelength of different modes

针对图6反映的问题，为了分析不同频率下的模态分解的精确性，这里通过矩阵条件数来分析模态分解的误差情况。如式(20)所示，径向模态分解时，其整体误差是由系统矩阵条件数κ(w)决定的，条件数定义为矩阵奇异值最大值与最小值之比，如式(21)所示。通过对人为构造周向模态幅值进行径向模态分解来检验其误差特性。因为0阶周向模态截通的径向模态个数最多，因此数值模拟中选择模拟m=0阶模态。数值模拟中阵列形状如图7所示，Nx为轴向测点数，Nr为径向测点数。为了探究实验中的误差传递特性，数值模拟设置的条件和实验相同，即轮毂比为0，沿机匣壁面布置14个等间距的传声器，其轴向间距用Δx表示，阵列可沿周向每隔6°进行测量。

(20)

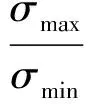
(21)

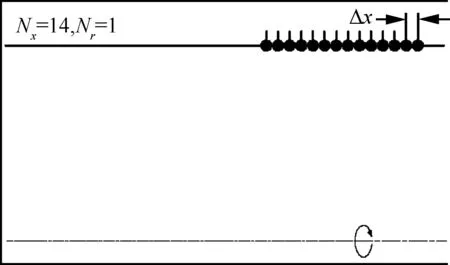
图7 旋转阵列布置方案Fig.7 Arrangement of rotating array

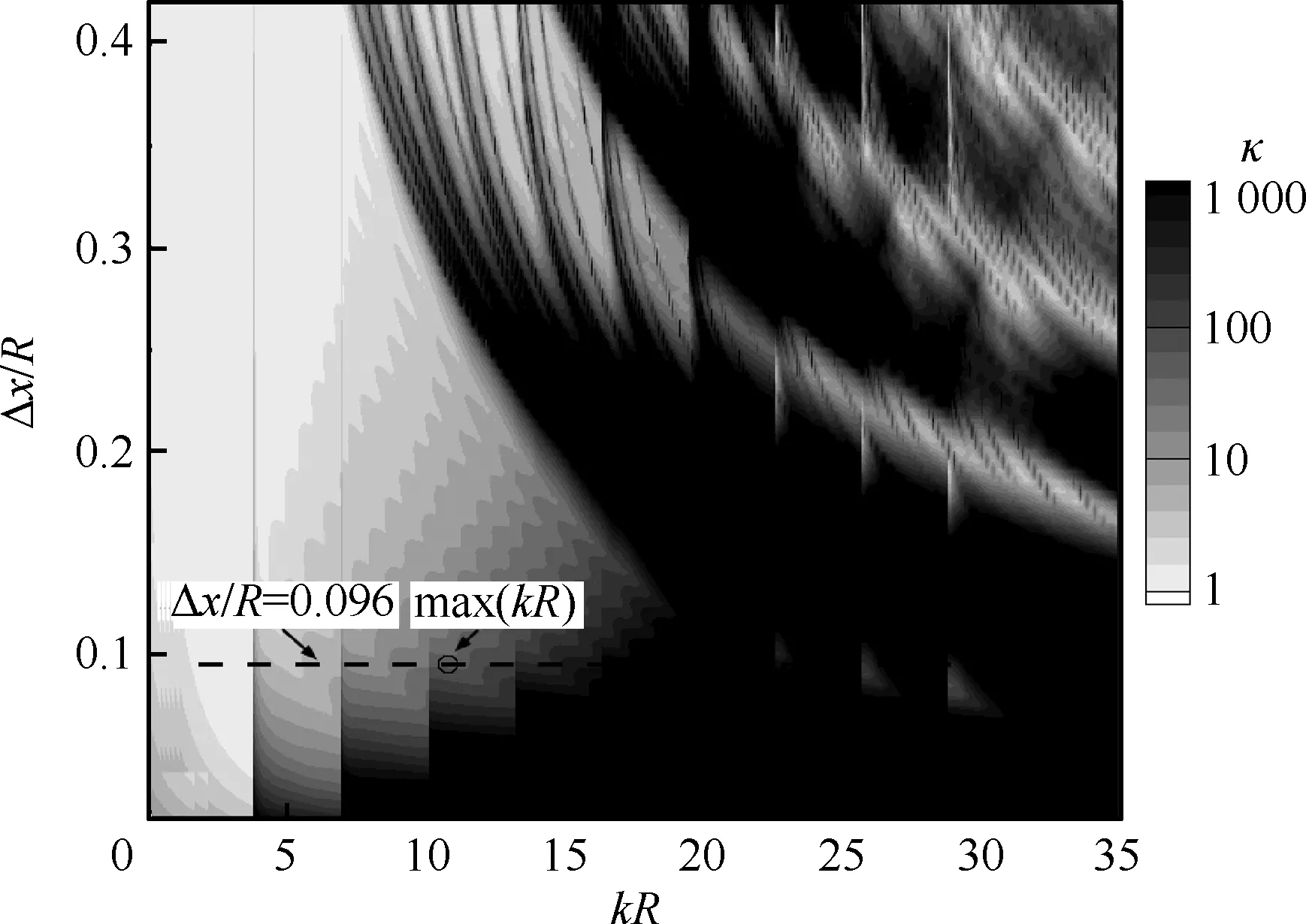
图8 不同频率和轴向间距下的条件数结果Fig.8 Condition number results of different axial interval at various frequencies

数值模拟出的条件数随频率以及阵列轴向间距变化特性如图8所示。如图所示当轴向间距固定时，随着更高阶径向模态截通，其条件数有一定跃升，这和模态分解理论是符合的。图中可以看出用轴向阵列进行模态分解，其轴向间距的设计并不是越小越好。随着频率增加，条件数变得越来越大，说明数值求解已经变得非常不可信。当阵列轴向间距固定下来时，在一定的误差限以内，存在一个最大求解频率max(kR),并且对于相同数目传声器组成的阵列，存在一个最佳轴向间距Δxopt,使得max(kR)最大化，这方面的研究会在后续论文中详细讨论。实验中真实的间距是Δx/R=0.096,在图中可以看出，在κ(w)≤100误差限内，可求解的最高无因次频率约为kR=11.5,对应频率为2 500 Hz。

在将2.2节介绍的参考相干方法应用于旋转测量装置(图3所示)之前，本文首先将其与现有的成熟测量方法[16]进行对比,从而验证该方法的准确性和可靠性。图9给出了上述两种方法计算出的声功率频谱结果，图中：RC对应于参考相干方法；CC对应于互相关方法[16]；PWL(PoWer Level)为声功率级。可以看出2种方法计算出的声功率结果量级和频谱形状都符合得很好。当频率f>397 Hz时，2种方法测量得到的宽频噪声量级最大相差1 dB。总的来说2种方法都可以准确地对管道内宽频噪声进行测量评估。

图10为各个模态的声功率频谱图，因为截通模态个数较多，为了更清晰和简洁地展示宽频范围内各个模态的能量分布规律，这里只挑选了其中的21个模态波。模态刚截通时，幅值都变得很大，这是数值误差引起的。因为当模态刚截通时，轴向波数近似为0(当轴向马赫数很小，即Max→0)，这时计算出的波长接近无穷大，理论上对这种波进行采样分析，需要在无穷长的尺度上布置测点才可以。声压级结果中，(1, 0)和 (2, 0)模态分别是1BPF和2BPF处的主导单音，这与理论是符合的。当频率较高时，各个模态的幅值变得很接近，也就是说各个模态在宽频范围内携带的能量接近相同，这与通常意义中的Equal Energy Per Mode(EEPM，每个模态携带相同能量)符合。

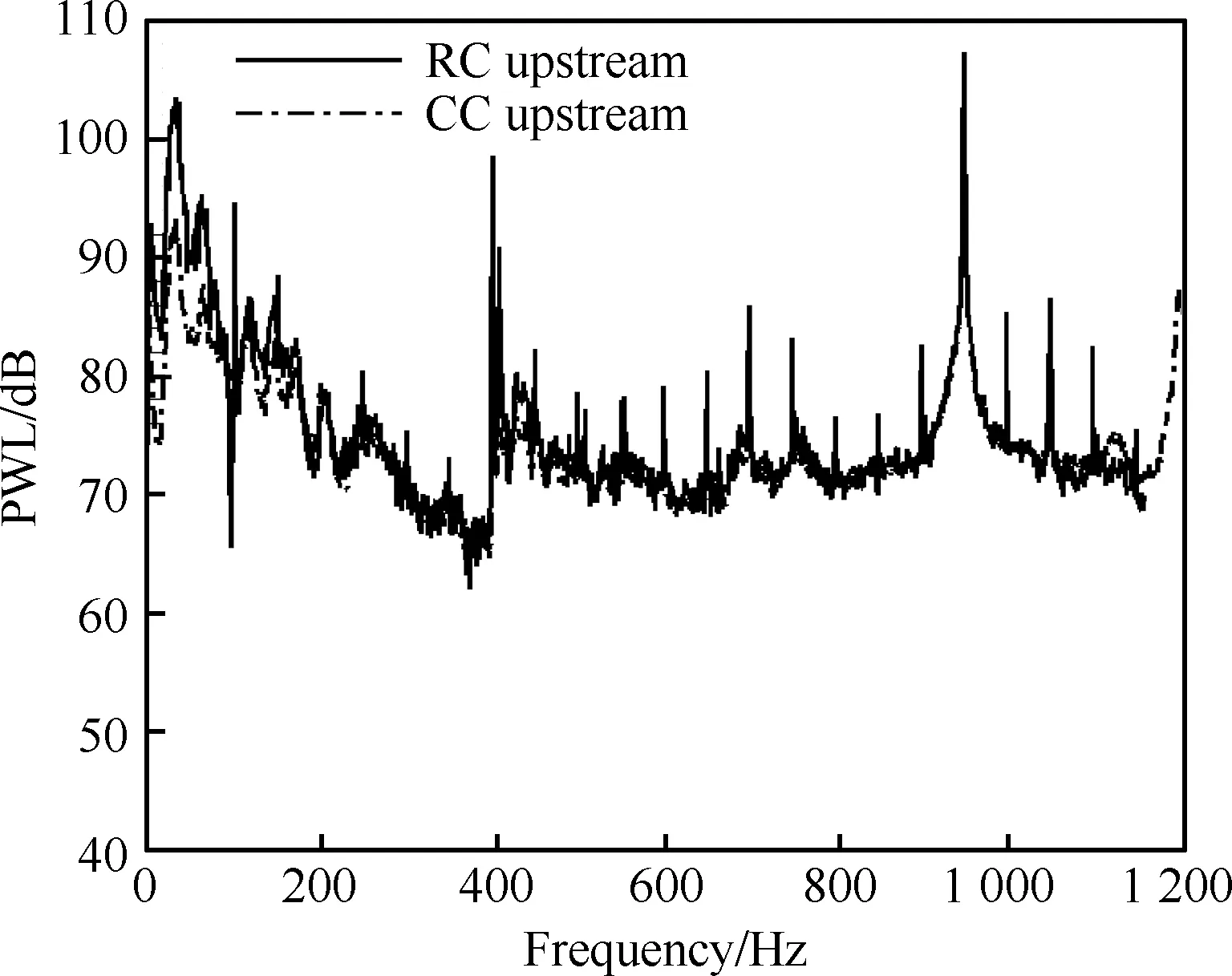
图9 两种方法计算出的声功率频谱Fig.9 Sound power spectrums calculated by two methods

假设每个模态携带的能量为ϖ,那么模态幅值可以写为

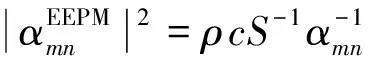
(22)

当Max≪1时，式(22)可以写为

(23)

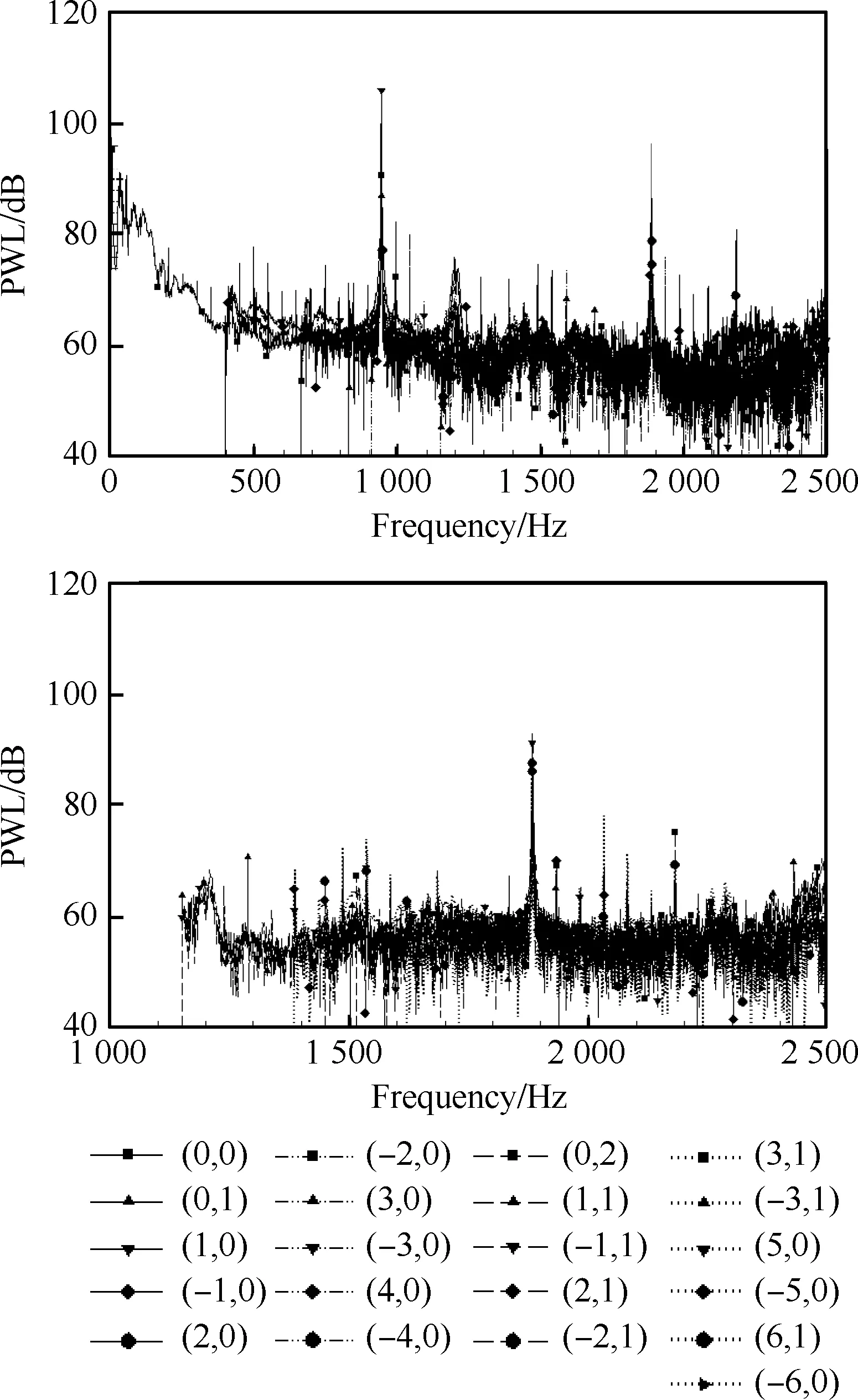
图10 模态声功率频谱Fig.10 Modal sound pressure spectra

图11 模态(0, 0)的声功率频谱Fig.11 Sound power spectrum of mode (0, 0)

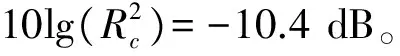
在上述的结果中，不管是单个模态声功率频谱还是管道内总声功率频谱，都在多个频率处出现了大量尖峰型“单音”，这些峰值出现的频率并不是模态截通频率或者转子通过频率。为了研究这些“单音”的产生源头，这里将计算出的功率频谱和传声器原始信号频谱进行对比分析。图13是原始声压信号的声压级结果和求解出的管道内声功率频谱对比图，其中声压级结果是所有测点平均的结果。图中可以看出两者频谱形状相同，只是相差一个恒定的数值。这与理论是符合的，因为声压级近似等于声强级，而声功率与声强级之间只差10lgS=-7.07,这与求解出的结果比较吻合。

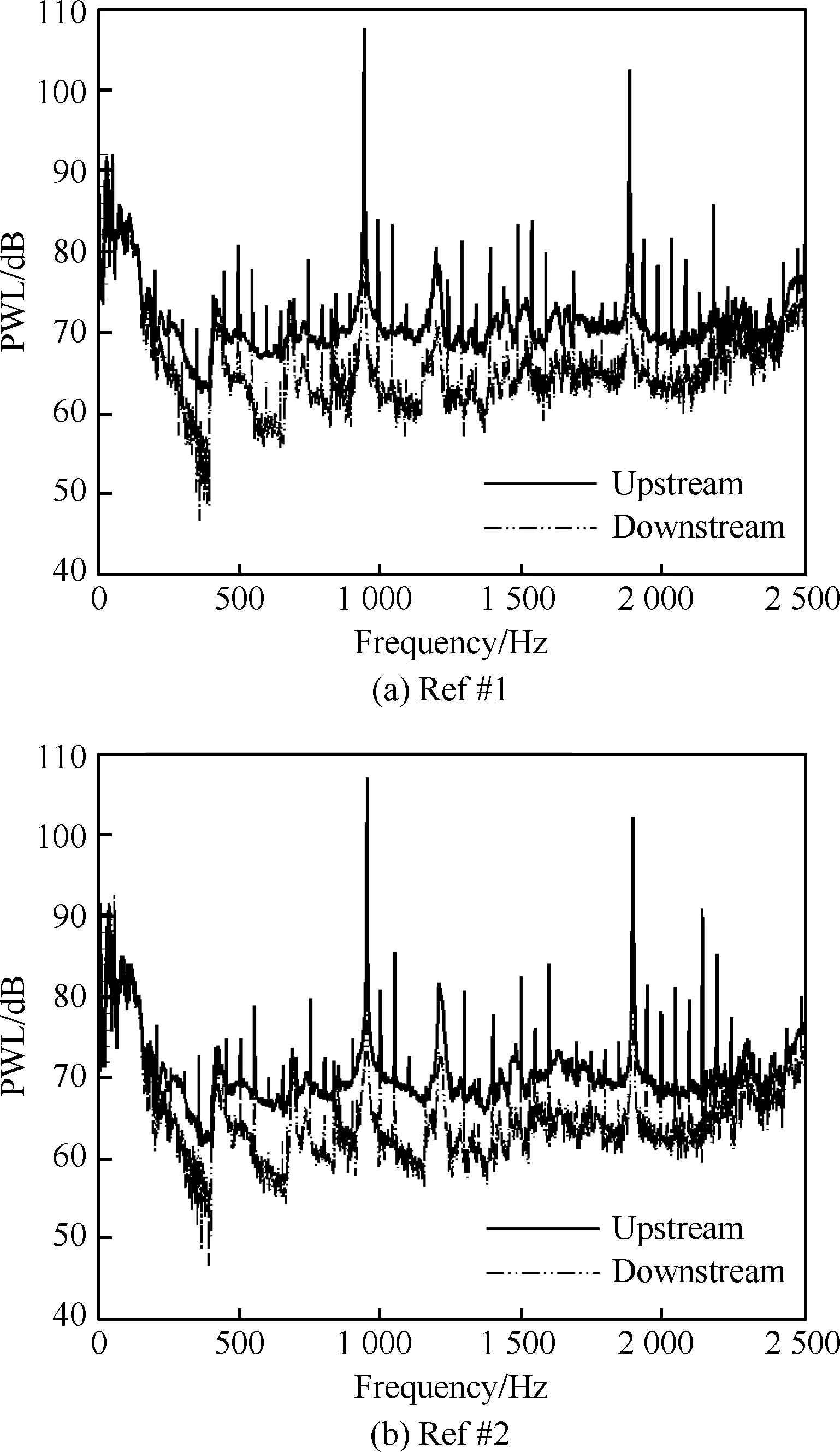
图12 顺流和逆流传播的声功率结果Fig.12 Results of sound power propagating upstream and downstream

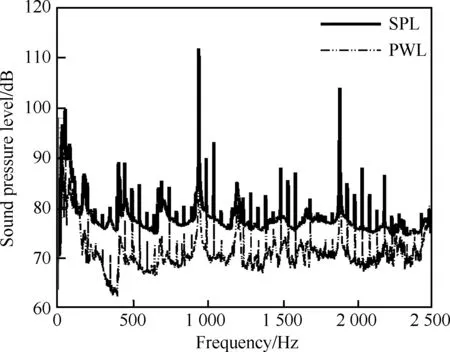
图13 声压级和声功率结果Fig.13 Sound pressure level and sound power results

4 结 论

1) 在半消声室内对风扇管道内的声场进行了测量，首次使用可周向旋转的阵列对管道内宽频噪声进行模态分解研究，结果表明可以成功地分辨出管道内部顺流和逆流传播的模态波，其中NPU-Fan的入射声波比反射声波能量更强，其声功率结果最大相差10 dB。

2) 使用不同参考信号计算出的声功率结果相同，这说明参考信号互相关方法对参考信号位置的选取没有特别的要求，进一步说明该方法有很好的鲁棒性，有很好的应用前景。

3) 随着模态截通比增大，模态之间变得更难分辨，这时使用轴向阵列对管道模态进行分解需要考虑到矩阵条件数对误差传递的影响，并可以用此指标来确定出可精确分辨声波的频率上限。

4) 模态声压级频谱结果表明，模态刚截通时，幅值都变得很大，这是数值误差引起的。在整个宽频范围内，各个模态的幅值变得很接近，说明宽频范围内各个模态携带的能量接近相同。

致 谢

感谢西北工业大学叶轮机械气动力学和气动声学实验室和中国飞机强度研究所三十二室、五室工作人员的大力支持。

[1] 乔渭阳.航空发动机气动声学[M]. 北京：北京航空航天大学出版社，2010：1-8.

QIAO W Y. Aero-engine aeroacoustics [M]. Beijing: Beijing University of Aeroacoustics & Astronautics Press, 2010:1-8 (in Chinese).

[2] TYLER J M, SOFRIN T G. Axial flow compressor noise studies[J]. Transactions of the Society of Automotive Engineers, 1962, 70(1):309-332.

[3] MORFEY C L. Rotating pressure patterns in ducts: Their generation and transmission[J]. Journal of Sound and Vibration, 1964, 1(1): 60-87.

[4] MORFEY C L. Sound transmission and generation in ducts with flow[J]. Journal of Sound and Vibration, 1971, 14(1): 37-55.

[5] JOSEPH P, MORFEY C L, LOWIS C R. Multi-mode sound transmission in ducts with flow[J]. Journal of Sound and Vibration, 2003, 264(3): 523-544.

[6] RICE E J. Modal density function and number of propagating modes in ducts: NASA-TM X-73539[R]. Washington, D.C.: NASA, 1976.

[7] RICE E J. Modal propagation angles in a cylindrical duct with flow and their relation to sound radiation: NASA-TM-79030[R]. Washington ,D.C.: NASA, 1979.

[8] FARASSAT F, MYERS M K. A study of wave propagation in a duct and mode radiation: NASA-TM-111590[R]. Washington, D.C.: NASA,1996.

[9] ABOM M. Modal decomposition in ducts based on transfer function measurements between microphone pairs[J]. Journal of Sound and Vibration, 1989,135(1): 95-114.

[10] CHUNG J Y. Rejection of flow noise using a coherence function method[J]. Journal of the Acoustical Society of America, 1977, 62(2): 388-395.

[11] MICHALKE A, ARNOLD F, HOLSTE F. On the coherence of the sound field in a circular duct with uniform mean flow[J]. Journal of Sound and Vibration, 1996, 190(2): 261-271.

[12] MICHALKE A. On experimental sound power determination in a circular pipe with uniform mean flow[J]. Journal of Sound and Vibration, 1990, 142(2): 311-341.

[13] MICHALKE A. On the propagation of sound generated in a pipe of circular cross-section with uniform mean flow[J]. Journal of Sound and Vibration, 1989,134(2): 203-234.

[14] ENGHARDT L, LOWIS C. Broadband sound power determination in flow ducts[C]∥10th AIAA/CEAS Aeroacoustics Conference.Reston, VA: AIAA, 2004.

[15] TAPKEN U, ENGHARDT L. Optimization of sensor arrays for radial mode analysis in flow ducts[C]∥12th AIAA/CEAS Aeroacoustics Conference.Reston, VA: AIAA, 2006.

[16] JÜRGENS W, TAPKEN U, PARDOWITZ B, et al. Technique to analyze characteristics of turbomachinery broadband noise sources[C]∥16th AIAA/CEAS Aeroacoustic Conference. Reston, VA: AIAA, 2010

[17] DAHL M D, HIXON R, SUTLIFF D L. Further development of rotating rake mode measurement data analysis[C]∥19th AIAA/CEAS Aeroacoustic Conference. Reston, VA: AIAA, 2013.

[18] TAPKEN U, BAUERS R, NEUHAUS L, et al. A new modular fan rig noise test and radial mode detection capability[C]∥17th AIAA/CEAS Aeroacoustic Conference, Reston, VA: AIAA, 2011.

[19] SPITALNY M, TAPKEN U. Radial mode analysis of ducted sound fields with sensor rakes and wall flush sensor arrays under consideration of radial flow profile[C]∥22nd AIAA/CEAS Aeroacoustics Conference. Reston, VA: AIAA, 2016.

[20] MUMCU A, KELLER C, HURFAR C M, et al. An acoustic excitation system for the generation of turbomachinery specific sound fields-Part I: Design and methodology[C]∥ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition. New York: ASME, 2016.

[21] HURFAR C M, KELLER C, MUMCU A, et al. An acoustic excitation system for the generation of tur-bomachinery specific sound fields-Part II: Experimental verification[C]∥ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition. New York: ASME, 2016.

[22] TADDEI F, LUCIA M D, TORZO D, et al. A comparison between radial rakes of sensors and axial arrays of microphones for the experimental investigation of tone noise in LPTs[C]∥19th AIAA/CEAS Aeroacoustics Conference. Reston, VA: AIAA, 2013.

[23] NELSON P A, YOON S H. Estimation of acoustic source strength by inverse methods: Part I, Conditioning of the inverse problem[J]. Journal of Sound and Vibration, 2000, 233(4): 639-664.

[24] KIM Y, NELSON P A. Estimation of acoustic source strength within a cylindrical duct by inverse methods[J]. Journal of Sound and Vibration, 2004, 275(1): 391-413.

[25] JOSEPH P, MOURIES F, ENGHARDT L. A two-microphone method for the estimation of the mode amplitude distribution in multi-mode broadband sound field in finite-length ducts with mean flow[C]∥20th AIAA/CEAS Aeroacoustics Conference. Reston, VA: AIAA, 2014.

Experimentaloffanbroadbandnoisedeterminationbasedonrotatingaxialarrays

XUKunbo1,*,QIAOWeiyang1,HUOShiyu2,CHENGHaoyi1,TONGFan1

1.SchoolofPowerandEnergy,NorthwesternPolytechnicalUniversity,Xi’an710072,China2.The32ndResearchLaboratory,AVICAircraftStrengthResearchInstitute,Xi’an710065,China

Toreduceaircraftenginenoise,ameasurementtechniqueisurgentlyneededforbroadbandnoisedeterminationinsidetheturbomachineryducttoguidenoisereductiondesign.Inthispaper,resultsofthesoundpowerpropagatingupstreamanddownstreamaredeterminedwithcross-correlationanalysisofsoundpressure.Themicrophonearraysinstalledupstreamofthefanrigconsistof2axialarrayswithcircumferentialintervalof180°,witheacharrayhaving14equidistantmicrophones.Arraysareinstalledonarotatingduct.Intheexperiment,theductrotatesonceper6°,andthesoundpressuredataof840positionsintotalareacquired.Theincidentsoundwavescanbeasmuchas10dBhigherthanthereflectedsoundwaves.Thedecomposedmodalresultsshowthatrotor-statorinteractionmodesarethedominantmodesatbladepassingfrequencyanditsharmonics.Thedecomposedresultsareconsistentwhendifferentsensorsareusedasreferencesignalsandthusthisexperimentalmethodisnotsensitivetothereferencesignalposition,showinggoodapplicabilityofthemethod.

broadbandnoise;mode;array;turbomachinery;fan

2017-01-15；Revised2017-05-15；Accepted2017-06-05;Publishedonline2017-06-121142

URL：http://hkxb.buaa.edu.cn/CN/html/20171102.html

s：NationalNaturalScienceFoundationofChina(51476134);China-EuropeanUnionInternationalCooperationProjectonAviationScience(688971)

.E-mailspiritkb@mail.nwpu.edu.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.121132

V231.3

A

1000-6893(2017)11-121132-11

2017-01-15；退修日期2017-05-15；录用日期2017-06-05;< class="emphasis_bold">网络出版时间

时间：2017-06-121142

http://hkxb.buaa.edu.cn/CN/html/20171102.html

国家自然科学基金 (51476134)；中国-欧盟航空科技国际合作项目(688971)

.E-mailspiritkb@mail.nwpu.edu.cn

许坤波，乔渭阳，霍施宇，等．基于旋转轴向阵列的风扇宽频噪声实验J．航空学报,2017,38(11):121132.XUKB,QIAOWY,HUOSY,etal.ExperimentaloffanbroadbandnoisedeterminationbasedonrotatingaxialarraysJ.ActaAeronauticaetAstronauticaSinica,2017,38(11):121132.

(责任编辑：张晗)