基于改进MDS的软件缺陷预测
史雪静,吴 飞,荆晓远,3
(1.南京邮电大学 计算机学院,江苏 南京 210003;2.南京邮电大学 自动化学院,江苏 南京 210003;3.武汉大学 计算机学院 软件工程国家重点实验室,湖北 武汉 430072)
基于改进MDS的软件缺陷预测
史雪静1,吴 飞2,荆晓远1,3
(1.南京邮电大学 计算机学院,江苏 南京 210003;2.南京邮电大学 自动化学院,江苏 南京 210003;3.武汉大学 计算机学院 软件工程国家重点实验室,湖北 武汉 430072)
随着计算机技术的发展,计算机软件产品给个人和企业都带来了很多方便,但很多软件也会存在各种缺陷。为了找到并解决软件中存在的缺陷,研究者将机器学习等方法应用到软件缺陷预测之中,但这些方法在数据预处理方面还存在很多需要改善的地方。在之前的研究中,有研究者使用多维尺度分析(MDS)对数据样本进行降维,但关于如何使用和改善MDS的方法却很少。文中提出了基于阈值相关性的多维尺度分析(TC_MDS)方法,在使用MDS方法的基础上,使用对称不确定性(SU)方法提取具有高鉴别的特征,并使用阈值相关性去除冗余特征。该方法学习得到的数据具有高鉴别性,去除了冗余特征,从而提高了预测效率。在软件工程NASA数据库上的实验结果表明,提出的方法具有较好的缺陷预测效果。
多维尺度分析;对称不确定性;阈值相关性;软件缺陷预测
0 引 言
软件缺陷预测可以预测软件出现的错误[1]。从整体上,软件缺陷预测可以分为动态缺陷预测和静态缺陷预测[2]。文中使用的是静态缺陷预测。
至今已有很多文献提出了静态软件缺陷预测算法,算法的核心有两点,一是挖掘软件度量,二是构建软件缺陷预测模型。目前已经有很多研究者将机器学习方法运用到软件缺陷预测中,例如K近邻分类器(K-Nearest Neighbor,KNN)、压缩C4.5模型(Compressed C4.5,CC4.5)[3]、朴素贝叶斯模型(Naïve Bayes,NB)[4]、支持向量机模型(Support Vector Machine,SVM)[5-6]、神经网络模型(Neural Networks,NN)[7-8]等。
软件度量即是与软件是否有缺陷密切相关的属性,FENTON等[9]将软件度量分为产品度量、过程度量、资源度量。这些度量能够描述一个软件模块的各种属性,预测模型就是在度量和缺陷类型上建立的关系,所以拥有高质量的软件度量尤为重要。主成分分析(Principal Component Analysis,PCA)[10]、线性鉴别分析(Linear Discriminant Analysis,LDA),拉普拉斯特征映射方法(Laplacian Eigenmaps,LE)[11]、多维尺度分析(Multi-Dimensional Scaling,MDS)[12-13]等都是针对软件质量进行的研究。
在研究MDS方法的基础上,文中使用对称不确定性(Symmetrical Uncertainty,SU)方法选出高鉴别性的特征,并去除冗余特征,提出了一种新的数据预处理方法,即基于阈值相关性的多维尺度分析(Threshold Correlation on Multi-Dimensional Scaling,TC_MDS)。在NASA数据库[14]上对该方法的有效性进行了验证。
1 多维尺度分析
MDS是一种维度降低的方法,通过分析相似数据来挖掘数据中的隐藏结构信息。通常,相似度量使用欧氏距离表示。所以,MDS算法的目的是在尽可能保留数据样本间距离的情况下,将数据样本映射到一个低维空间,以此降低样本的维度。
给定一组训练样本X={xi,li},i=1,2,…,n,其中训练样本xi∈Rd,d是样本维数,li(li∈{1,2,…,c})是样本类别标签。两个样本之间距离由欧氏距离定义为:
d(xi,xj)=(xi-xj)T(xi-xj)
(1)
每对样本间的距离组成的矩阵作为相似矩阵。
(2)
MDS的目标是给定D,构造样本Z={zi,li},i=1,2,…,n,使得‖zi-zj‖≈di,j,其中i,j∈1,2,…,n。可将MDS的解决看作一个优化问题,通过最小化下面的代价函数,可求得
(3)
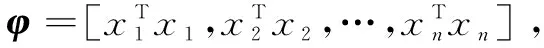
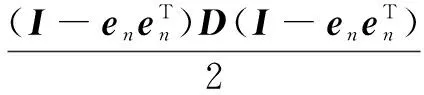
(4)
通过广义特征值求解方法计算T的特征值和特征向量,取前m(m (5) 文中在MDS的基础上进行改进,引入方法SU[15]。SU作为非线性的相关性度量,使用的理论来自信息论中的熵。该方法可以用来评估特征的质量。对于两个变量X和Y,SU的计算公式如下: (6) 其中,H(X)为变量X的熵。 假设p(x)是X取值的概率,则H(X)为: (7) IG(X|Y)为信息増益,定义为: IG(X|Y)=H(X)-H(X|Y)=H(Y)-H(Y|X) (8) SU(X,Y)=1意味着通过任意一个变量的取值能完全预测另一变量的值;SU(X,Y)=0则表明X和Y之间相互独立。 虽然MDS方法获得的新样本在降低计算复杂度的同时包含了尽可能多的原样本信息,但是该方法对分类效果改善很少,通过使用SU方法选取与类别相关性较高的特征可以提高新样本的鉴别性。另外,MDS无法去除冗余特征,即降维后的样本可能会含有冗余特征,这会降低算法的效率,所以文中使用阈值相关性方法去除冗余特征。 由此,TC_MDS的实施步骤如下: (1)使用MDS对样本集降维; (2)使用SU方法计算每个特征与类别的相关度,提取具有高鉴别性的特征; (3)使用阈值相关性方法去除冗余特征。 在实际软件度量中,存在非线性的关系,所以文中依然选择SU来计算一对特征间的相似度。文中的阈值相关性方法使用预设的β作为相关性的临界值,在步骤(2)得到的特征下,从后向前对每个特征进行相关性分析,所有大于临界值的一对特征就从样本集中去除靠后的特征,然后以此类推。之所以从后向前进行相关性分析,是因为步骤(2)得到的特征从后往前其鉴别性越来越高,所以从后往前进行相关性分析,当遇到相关度大于β值的两个特征时,就可以优先去掉鉴别性小的特征,从而保留鉴别性较大的特征。 TC_MDS算法描述如下: 输入:训练样本集X=[X1,X2,…,Xc],其中Xi=(F1,F2,…,Fm,L),i=1,2,…,c,相关性阈值β; 输出:样本集Z。 步骤1:计算各个样本之间的距离,得到距离矩阵D; 步骤3:令i=1 tok,循环 计算Si=SU(Fi,L); 步骤4:对Si按从大到小排序; 步骤6:对每对特征从后向前使用SU进行相关性分析,去除大于β的指定特征,得出最终样本Ζ。 选用NASA数据库,五个工程分别代表着NASA的软件系统,它们具有不同的度量和对应的缺陷标记。表1汇总了这五个工程的详细信息。 表1 NASA数据集 实验中使用四种评估指标,分别是召回率(Recall,Pd)、误检率(Pf)、F-measure和ROC曲线下的面积(AUC)。预测结果见表2。 指标定义为: Pd=A/(A+B) (9) Pf=C/(C+D) (10) F-measure=2*recall*precision/(recall+ precision) (11) 其中,precision=A/(A+C)。 当具有较高的Pd,F-measure,AUC和较低的Pf,一个预测模型才算是好的。且F-measure和AUC是综合性评价指标,更为重要。 实验使用MDS、PCA、LE作为对比方法,使用随机森林作为分类器,在CM1、MW1、PC1、PC3、PC4库中进行实验,结果见表3。 表3 实验结果 分析表3可知,提出的方法TC_MDS在各个数据库上的缺陷预测效果普遍好于其他方法,尤其是F-measure和AUC,对比PCA、LE以及MDS优势明显,说明了该方法在缺陷预测中的优势。 在MDS的基础上,使用SU方法提取有鉴别性的特征,并使用阈值相关性方法去除冗余特征,提出一种新的数据预处理方法(TC_MDS)。该方法学习得到的数据具有很好的鉴别性,并去除了冗余特征,提高了运算效率,降低了复杂度。在NASA数据库上的实验结果表明,TC_MDS与现有的代表性缺陷预测方法相比,明显提高了缺陷预测的效率。 [1] 李 勇,黄志球,房丙午,等.代价敏感分类的软件缺陷预测方法[J].计算机科学与探索,2014,8(12):1442-1451. [2] 王 青,伍书剑,李明树.软件缺陷预测技术[J].软件学报,2008,19(7):1565-1580. [3] WANG J,SHEN B J,CHEN Y T.Compressed C4.5 models for software defect prediction[C]//International conferenceon quality software.[s.l.]:IEEE,2012. [4] TAO W,LI W H.Naive Bayes software defect prediction model[C]//International conference on computational intelligence and software engineering.Wuhan,China:IEEE,2010:1-4. [5] ELISH K,ELISH M.Predicting defect-prone software modules using support vector machines[J].Journal of Systems and Software,2008,81(5):649-660. [6] SHEPPERD M,BOWES D,HALL T.Researcher bias:the use of machine learning in software defect prediction[J].IEEE Transactions on Software Engineering,2014,40(6):603-616. [7] QUAH T S,THWIN M M T.Application of neural networks for software quality prediction using object-oriented metrics[C]//International conference on software maintenance.[s.l.]:IEEE,2003:589-590. [8] ZHENG J.Cost-sensitive boosting neural networks for software defect prediction[J].Expert Systems with Applications,2010,37(6):4537-4543. [9] FENTON N E,NEIL M.Software metrics:roadmap[C]//Proceedings of conference on the future of software engineering.[s.l.]:[s.n.],2000:357-370. [10] 刘 旸.基于机器学习的软件缺陷预测研究[J].计算机工程与应用,2006,42(28):49-53. [11] BELKIN M,NIYOGI P.Laplacian eigenmaps for dimensionality reduction and data representation[J].Neural Computation,2003,15(6):1373-1396. [12] BRUCHER M,HEINRICH C,HEITZ F.A metric multidimensional scaling-based nonlinear manifold learning approach for unsupervised data reduction[J].Eurasip Journal on Advances in Signal Processing,2008(1):1-12. [13] LU H,CUKIC B,CULP M.A semi-supervised approach to software defect prediction[C]//Computer software and applications conference.[s.l.]:IEEE,2014:416-425. [14] MENZIES T,GREENWALD J,FRANK A.Data mining static code attributes to learn defect predictors[J].IEEE Transactions on Software Engineering,2007,33(1):2-13. [15] 陈家强.软件缺陷预测中数据预处理技术研究[D].南京:南京大学,2014. SoftwareDefectPredictionBasedonImprovedMDS SHI Xue-jing1,WU Fei2,JING Xiao-yuan1,3 (1.School of Computer,Nanjing University of Posts and Telecommunications,Nanjing 210003,China;2.School of Automation,Nanjing University of Posts and Telecommunications,Nanjing 210003,China;3.State Key Laboratory of Software Engineering,School of Computer,Wuhan University,Wuhan 430072,China) With the development of computer technology,computer software products have brought many convenience to individuals and businesses,but many software may have a variety of defects.In order to find and solve them,researchers have applied machine learning and other methods in software default prediction,but they need to be improved on data preprocessing.In previous studies,the researchers used Multi-Dimensional Scaling (MDS) to reduce the dimensionality of data samples.But the methods about how to use and improve MDS are few.A method of Threshold Correlation on MDS (TC_MDS) is proposed in this paper.Based on MDS,Symmetrical Uncertainty (SU) is used to extract the features with high discriminatory and threshold correlation to remove the redundancy.The method makes the data with high discriminatory,removing of redundancy,improvement of forecasting efficiency.The results on NASA database show it has very good defect prediction effect. MDS;symmetrical uncertainty;threshold correlation;software defect prediction TP31 A 1673-629X(2017)12-0020-03 10.3969/j.issn.1673-629X.2017.12.005 2017-01-20 2017-05-25 < class="emphasis_bold">网络出版时间 时间:2017-09-27 国家自然科学基金资助项目(61272273) 史雪静(1991-),女,硕士研究生,研究方向为软件缺陷预测;吴 飞,讲师,研究方向为机器学习、软件工程;荆晓远,教授,博士生导师,研究方向为模式识别、图像与信号处理、信息安全、机器学习与数据挖掘。 http://kns.cnki.net/kcms/detail/61.1450.TP.20170927.1000.072.html2 基于阈值相关性的多维尺度分析

3 实 验
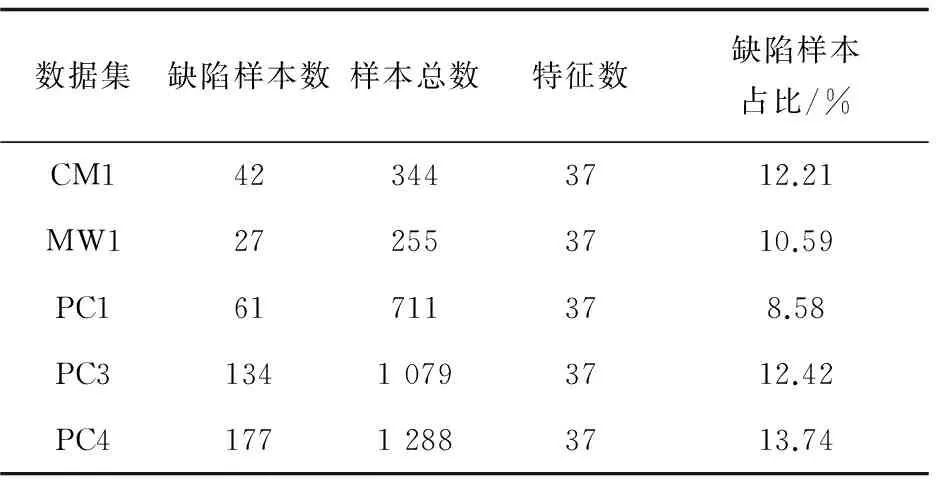
3.1 数据库
3.2 性能评价指标
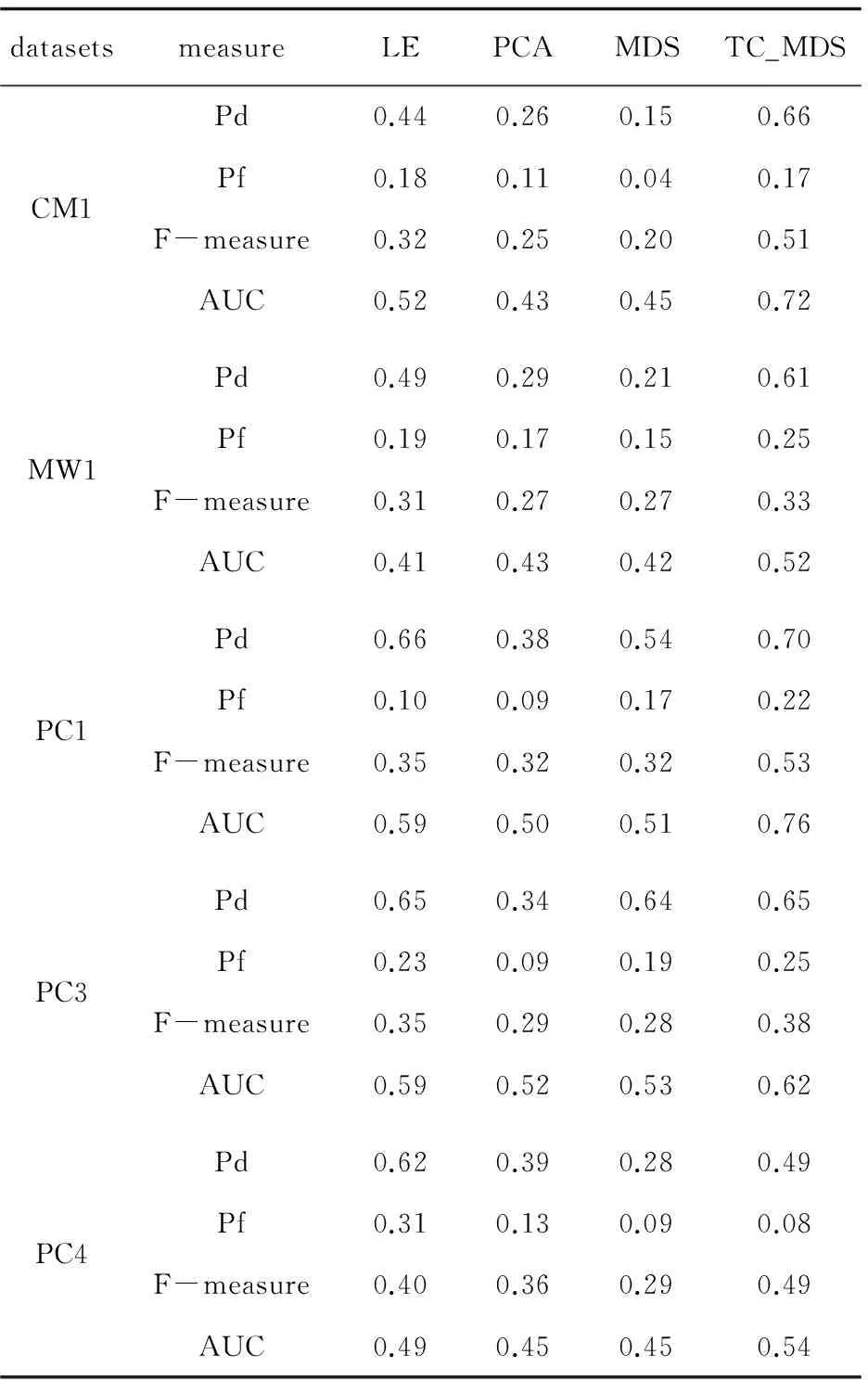
3.3 实验结果与分析
4 结束语

