基于Kinect动态手势识别算法的研究与实现
张莹莹,郭 星
(1.安徽大学 计算智能与信号处理重点实验室,安徽 合肥 230039;2.安徽大学 计算机科学与技术学院,安徽 合肥 230601)
基于Kinect动态手势识别算法的研究与实现
张莹莹1,郭 星2
(1.安徽大学 计算智能与信号处理重点实验室,安徽 合肥 230039;2.安徽大学 计算机科学与技术学院,安徽 合肥 230601)
随着计算机技术和信息化的发展,人机交互在办公以及生活中显得越来越重要。由于手势具有灵活、直观、简单等优点,成为人机交互研究的重要领域。针对手势识别技术在自然人机交互中对时间和准确度要求较高的问题,提出一种新的手势识别算法(IDTW-K)。该算法对经典动态时间规整(Dynamic Time Warping,DTW)算法进行了改进。利用节点在运动序列中的距离方差对各个节点进行权值动态分配,并对DTW的搜索路径进行了详细的分析,采用点和线相结合的范围约束防止其搜索不合理以及优化DTW算法的计算速度,并结合KNN算法提高了手势识别效率。通过实验对IDTW-K算法、改进的DTW算法和传统的DTW算法进行了对比,结果表明所提出的算法在精准度和识别速率上有一定的提高。
人机交互;特征提取;手势识别;加权动态时间规整算法;K近邻算法
0 引 言
近年来,由于计算机技术的发展,人机交互在实际生活中越来越重要[1]。人机交互也由传统的输入设备(如鼠标、键盘等)逐步向以语音、动作等智能的输入设备发展。其中由于手势具有简单、灵活、易懂等优点,广泛应用于动作识别的研究领域中。手势识别作为一种智能的输入设备具有广泛的应用前景,例如智能家居、智能游戏以及先进的教育产品等。
国外学者对于手势识别技术的研究起步较早。1983年,Grimes提出手势识别并最早采用佩戴数据手套进行识别的方式。2011年,J.L.Raheja提出了利用Kinect跟踪手指间和手掌中心的方法。G.F.He等在利用Kinect分割出手部区域后,使用Graham Scan算法进行各个手指的区分等等[2]。目前,研究较多的是隐马尔可夫算法(HMM)[3]、神经网络算法、支持向量机(SVM)和动态时间规则算法(DTW)[4]。DTW算法在分类长短不同的序列上有绝对优势,这是前几种算法不可代替的。Carmona等对DTW算法应用于手势识别进行了研究,并强烈建议使用DTW算法代替HMM算法[4]。因此文中选用DTW算法进行手势识别。
由于Kinect对于获取人体相关的骨架节点信息有着简单、方便的特性[5],常被研究人体动作的研究者作为获取特征信息的工具。文中则是用Kinect来获取有关手势的骨架节点信息。在DTW算法中,为了提高手势识别的效率,考虑不同手势中各关键节点运动的差异,根据不同的骨架节点在运动中的方差进行权值的动态分配。传统DTW算法自身存在计算量和存储空间比较大的缺点。针对这些缺点,对DTW算法的搜索路径进行了线与点结合的约束,只计算可能遍历到的节点数据,降低计算量,提高识别效率。若选取的测试样本与训练样本的帧数相差很大或测试样本与其他已知类别的训练样本最小欧氏距离相等时,误差比较大,识别效率低。对此,文中结合DTW算法和KNN算法进行手势识别,并对其进行实验验证。
1 手势识别
手势识别包括手势分割、特征提取、手势建模和手势识别这几个主要过程[6]。通过手势识别的整个过程可以看出,对手势进行识别的主要依据就是提取的特征参数,所有的手势识别都是根据一定的特征参数来进行不同的分类。因此选择一组好的特征参数对于手势识别至关重要。
1.1 手势特征提取
对相同样本空间提取不同的特征参数进行识别,效果可能区别很大,因此特征参数的提取至关重要。由于每个人的高矮胖瘦不一或Kinect的摆放位置不同,对同一种手势Kinect获取的骨架节点的三维数据也不同[7],针对该问题,提出利用球面坐标[8-9]的方法求各关节点到躯干关节点的距离和与此距离有关的两个方位角度,作为节点的新信息。

图1 球面坐标示例
如图1所示,三维直角坐标系中的点p(x,y,z)对应球坐标中的序列为(γ,θ,φ)。其中,γ表示球面的点P到圆心O的距离;θ表示有向线段OP与Z轴正方向的夹角;φ表示P点映射在XOY面的点M与原点的有向线段OM与X轴正方向的夹角。文中选取躯干关节点作为球面的原点O,分别计算选取的关节点在球面坐标系中的表示。对Kinect获得的骨架节点数据,通过上述归一化处理后,避免了不同身高、胖瘦人体信息对实验的影响。
在大部分的手势识别中主要涉及到的关键节点有:左手,左手腕,左手肘,右手,右手腕,右手肘。文中通过Kinect获取用户骨骼框架的信息,从中提取实验所需的这六个节点的数据并进行归一化处理。手势关键节点的数据集合为P={PLH,PLE,PLS,PRH,PRE,PRS}。
1.2 手势识别算法
1.2.1 传统动态时间规整算法
动态时间规整[10](Dynamic Time Warping,DTW)最初主要用于语音识别,解决同一句话不同人说出的时间长短不一的问题。在手势识别中,针对同一种手势,不同的人其完成时间不一样[11]。然而隐马尔可夫方法需要经过大量的训练样本进行训练和数据统计,相对于简单的手势识别过于复杂;基于神经网络[12]的方法,虽然具有很强的抗干扰性和较强的分类能力,但对手势序列长度不一的情况处理能力明显降低。因此,文中采用DTW算法进行手势识别。
假设参考模板为R{R(1),R(2),…,R(M)},测试模板为T{T(1),T(2),…,T(N)}。其中R(m)和T(n)分别表示参考模板和测试样本的第m帧和第n帧的动作特征矢量,两者间的维数是相同的,M不一定等于N。通过R,T之间的距离D[R,T]来衡量测试样本和模板之间的相似度,d(R(m),T(n))表示任意两帧之间的距离。DTW算法中训练样本和测试样本在时间上是非线性映射的,这种映射关系表示为:(m1,n1),(m2,n2),…,(mf,nf),则:
(1)
其中,D越小其相似度就越高,D越大则相似度就越低。
整个计算过程可以看成M*N的矩阵,T表示横坐标,R表示纵坐标,计算量较大。根据Bellman最优原理:求D的最小值就是计算开始的节点(n0,m0)到终点(nf,mf)的最小路径。其中(n,m)表示参考模板与测试样本之间的交汇点。若起始点(n0,m0)表示为(0,0),(n0,m0)的下一个节点(n1,m1)只有三种选择,交汇点为(0,1),(1,0),(1,1)。求得这三个交汇点的代价d,代价最小的交汇点就是下一个节点。依次类推,直到找到最终的节点(nf,mf)为止。即
Dmin(nk,mk)=minDmin(nk-1,mk-1)+d(nk,mk)
(2)
其中,(nk-1,mk-1)是(nk,mk)的前一个节点。
最终通过比较测试样本与各参考模板之间的D值来划分属于哪一类。
1.2.2 新动态时间规整算法
在手势识别的过程中,不同的关节点在不同的手势中所起到的作用不同。例如画直线,手肘关节点基本是不动的,在使用右手做动作时左手基本保持静止状态。因此可以在计算时,针对不同的节点状态分配不同的权值[13],以提高手势识别效率。
按照关节点的运动剧烈程度(关节点的运动方差[14]Si)进行权值分配。其中相邻两帧间第i个节点的欧氏距离为Disti(pn,pn-1)。考虑到提取的手势分别为左、右手相关的三个节点,在用左手做动作时,右手相关的三个节点基本不动,故在分配权值时重点考虑前三个大小的方差。因此,规定后三个方差Si其阈值为Sa。权值分配公式如下所示:

(3)
其中,ωi表示节点i的权重;β的最佳值计算方法如下:

(4)
其中,SA(β)是所有训练样本的类间方差,SB(β)是所有训练样本的类内方差,则最优参数β的取值为:
β=argmax(R(β))
(5)
因此,训练样本和测试样本的相邻帧之间的距离d(R(m),T(n))为:
(6)
传统DTW算法的计算量和存储空间较大[15],需要计算一个M*N矩阵。为了提高DTW算法的速度,可以减少所需要遍历的点。通过上文对DTW算法的分析,测试样本与参考模板在识别中寻找下一个节点时,其位置只有可能在三点上,如图2所示。当前点若为(0,0),则下一个点只可能是(0,1),(1,0),(1,1)中的一个。因此很多节点不需要参与计算,能减少很大的计算量。
然而,DTW算法对于测试样本与两个不同类别的训练样本的欧氏距离相同时,无法判断测试样本的类别[16]。例如,模板为R1{1,1,1,1,1,1,1,1,4,4}和R2{1,1,2,2,3,2,4,4},测试样本为T{1,2,3,4},通过DTW算法计算得DTW(R1,T)=2,DTW(R2,T)=2。此时测试样本与两个模板的距离相同,不能识别手势。根据R1与T的DTW匹配路径,测试样本T被“拉成”{1,1,1,1,1,1,2,3,4,4}来进行一一匹配。这样的“拉伸”是不合理的,因此导致上述识别的失败。
对此,文中提出用两条斜线进行路径搜索的约束,如图2所示。在两条斜线的约束范围内搜索可能的节点,防止测试样本被不合理的“拉伸”。在计算时结合这两点特性进行DTW算法的路径搜索,大大降低了计算量,在提高速率的同时也提高了效率。

图2 DTW算法路径约束示意图
通过对DTW的改进,若出现同一类别的动作选择的训练样本与测试样本之间的时间相差较大,则计算出的欧氏距离较大,导致识别误差增大。因此文中提出结合简单的KNN算法进行综合识别,提高了识别效率。
1.2.3 KNN分类器
KNN算法在分类算法中很常用,也比较简单。它的核心思想是,若确定了近邻样本(靠近测试样本的训练样本)数K的值,即在最小的范围内找到K个训练样本,则训练样本数最多的这一类就是测试样本的类别。
KNN算法基本步骤如下:
(1)算距离:给定测试样本,计算测试样本与每个参考样本的距离;
(2)找近邻:将步骤1中计算的距离从小到大进行有序排列,确定K的值;
(3)做分类:统计K个近邻样本的类别,找出样本数最多的类别,即为测试样本的类别。
图3为KNN的工作原理示意图。圆形标记为测试样本,三角标记和方形标记分别表示两种已知类别的样本。当K=3时,测试样本类别与三角标记样本类别一致;当K=5时,测试样本类别与方形标记样本类别一致。
1.2.4 改进后的手势识别算法
根据上文描述,文中提出一种新的算法即IDTW-K算法。该算法将改进的DTW算法与KNN算法相结合,通过计算测试样本与各训练样本之间的可信度值确定测试样本的类别。

图3 KNN分类算法
设Ci代表类别,T代表测试样本,Ri为近邻中属于Ci类的训练样本,K为近邻的样本总数,Ki为近邻样本属于Ci类的样本个数。L(Ci,T)为T对Ci的类别可信度,计算公式为:
(7)

手势识别算法的步骤可归纳如下:
(1)分别计算测试样本和参考模板中所有节点移动的方差;
(2)对求得的方差进行排序,后三个节点的方差设为固定值Sa,根据式(3)进行动态的权值分配;
(3)使用改进的DTW算法计算测试样本与所有训练样本的欧氏距离;
(4)将步骤(1)中求得的欧氏距离从小到大进行有序排列,给定K值的大小,选择前K个近邻的训练样本,并标记这K个样本的类别Ci,计算其所属类别的个数Ki;
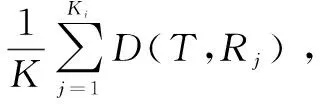
(6)比较Ci类的可信度大小。可信度最大的近邻样本的类别为测试样本的类别,若所有类别的训练样本与测试样本的可信度值都低于La,则判断此动作为无效动作,从而达到识别不同手势的效果。
2 实 验
通过识别手势的概率来衡量一个算法的好坏。文中通过识别左手和右手分别对向右画箭头、向左画箭头和画圆这三个动作,对比传统的DTW算法、改进后的DTW算法以及文中提出算法的识别效率和识别速度。
2.1 实验过程
在VS2010环境下进行实验,通过Kinect获取人的骨架节点信息。实验中选取20个同学,每个同学分别用左手和右手做了向左画箭头、向右画箭头和画圆的六个动作进行5次重复操作,设置Kinect以1 s获取20帧的速度对人的骨架节点进行捕获。提取捕获到的7个有用的骨架节点:左手、左手腕、左手肘、右手、右手腕、右手肘和人体的躯干节,然后根据提出的球面坐标原理进行标准化处理。计算测试样本序列T{T(1),T(2),…,T(N)}中相邻帧(以连续的3帧为相邻帧)节点的方差Si,根据式(3)进行节点权值的分配。其中Sa的取值为方差有序序列的后三位的均值。
图4所示为实验过程中由彩色图像获得人的深度图像,最后得到人体的骨架节点信息。

深度图 骨骼图 图像
2.2 实验结果
实验中,给出对DTW算法在路径约束的两条直线斜率均为1,且到直线y=x的水平距离不大于4。对比三个有关DTW算法手势识别的实验结果,如表1所示。

表1 算法的正确率
普通的DTW算法的计算量较大,分类识别的效果不是特别理想,一般在分类识别时不会直接使用。文中对DTW算法的寻优路径进行约束的同时考虑到分类识别中不同特征参数的重要性,对不同的特征参数进行权值分配来提高手势识别的效率。表1证明了文中对DTW算法的改进是有效的。由于KNN算法比较简单,易学易掌握,识别时间复杂度较小,但其自身识别效果不是很好。因此文中提出了结合KNN算法与改进DTW算法来提高手势识别的效率,并证明了该想法是可行的。
在提高实验效率的同时,对比三种算法的实验速度。选择右手向右画箭头、向左画箭头和画圆这三个动作并进行识别时间的统计,计算其平均处理时间(单位:ms),如图5所示。
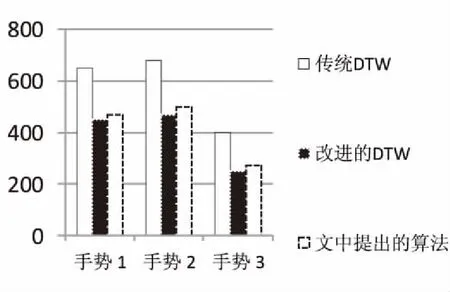
图5 耗时对比
从图中可以看出,改进后的DTW算法比传统的DTW算法在耗时上提高了30%~35%,而文中提出的算法比改进DTW算法的耗时有所增加,但幅度较小。
3 结束语
文中提出结合DTW算法和KNN算法进行综合计算,从而识别测试样本。同时,针对DTW算法自身计算量大这一缺点,提出对特征参数进行权值分配和搜索路径进行约束的方法。实验结果证明了该算法的有效性。
[1] 薛俊杰,陈健美.基于加权DTW手势识别方法的研究与实现[J].信息技术,2015,39(11):125-129.
[2] 吴晓雨,杨 成,冯 琦.基于Kinect的手势识别算法研究及应用[J].计算机应用与软件,2015,32(7):173-176.
[3] 常亚南.基于HMM的动态手势识别[D].广州:华南理工大学,2012.
[4] Carmona J M,Climent J.A performance evaluation of HMM and DTW for gesture recognition[M]//Progress in pattern recognition,image analysis,computer vision,and applications.Berlin:Springer,2012:236-243.
[5] 冯志全,蒋 彦.手势识别研究综述[J].济南大学学报:自然科学版,2013,27(4):336-341.
[6] Zhang Zhengyou.Microsoft Kinect sensor and its effect[J].IEEE Multimedia,2012,19(2):4-10.
[7] 郭 雷.动态手势识别技术综述[J].软件导刊,2015,14(7):8-10.
[8] 赵飞飞,刘喆颉,吕玉祥.基于Kinect骨骼信息的手势识别[J].中国科技论文,2015,10(20):2412-2415.
[9] 吴彩芳,谢 钧,俞 璐.基于骨骼和深度信息的手势识别的研究与应用[J].计算机技术与发展,2016,26(8):200-204.
[10] 刘 阳,尚赵伟.基于Kinect骨架信息的交通警察手势识别[J].计算机工程与应用,2015,51(3):157-161.
[11] 黄菲菲,曹江涛,姬晓飞.基于多通道信息融合的双人交互动作识别算法[J].计算机技术与发展,2016,26(3):58-62.
[12] Chen Lingchen,Wang Feng,Deng Hui,et al.A survey on hand gesture recognition[C]//International conference on computer sciences & applications.Wuhan:IEEE,2013:313-316.
[13] Reyes M,Dominguez G,Escalera S.Feature weighting in dynamic time warping for gesture recognition in depth data[C]//IEEE international conference on computer vision workshops.[s.l.]:IEEE,2011:1182-1188.
[14] 汪成峰,陈 洪,张瑞萱,等.带有关节权重的DTW动作识别算法研究[J].图学学报,2016,37(4):537-544.
[15] Hussain S M A,Rashid H U.User independent hand gesture recognition by accelerated DTW[C]//International conference on informatics electronics&vision.[s.l.]:[s.n.],2012:1033-1037.
[16] 李 凯,王永雄,孙一品.一种改进的DTW动态手势识别方法[J].小型微型计算机系统,2016,37(7):1600-1603.
ResearchandRealizationofDynamicalGestureRecognitionAlgorithmBasedonKinect
ZHANG Ying-ying1,GUO Xing2
(1.Key Laboratory of Intelligent Computing & Signal Processing of MoE,Anhui University,Hefei 230039,China;2.School of Computer Science and Technology,Anhui University,Hefei 230601,China)
With the development of computer technology and informatization,human-machine interaction is becoming more and more important in office and life.Due to the advantages of flexibility,intuition and simplicity for gesture, gesture recognition becomes a significant field in the study of human-machine interaction.According to the problem that gesture recognition has high requirements on time and accuracy in natural human-machine interaction,a new algorithm named IDTW-K is proposed with which the Dynamic Time Warping (DTW) is improved.It makes use of the variance of each node in the action sequence to distribute the weights and analyzes search path of DTW in detail,and then uses the range of constraints in combination of line and point to prevent its unreasonable search and optimize calculation speed of DTW,increasing efficiency of gesture recognition combining K-Nearest Neighbor (KNN).The experiments make a comparison of the IDTW-K,the improved DTW and the traditional DTW,which show that the proposed algorithm improves the accuracy and recognition efficiency.
human-machine interaction;feature extraction;gesture recognition;weighted dynamic time warping;K-nearest neighbors
TP301.6
A
1673-629X(2017)12-0011-05
10.3969/j.issn.1673-629X.2017.12.003
2016-11-11
2017-03-16 < class="emphasis_bold">网络出版时间
时间:2017-08-01
国家科技支撑计划(2015BAK24B01)
张莹莹(1991-),女,硕士研究生,研究方向为模式识别;郭 星,博士研究生,讲师,研究方向为模式识别、计算机视觉。
http://kns.cnki.net/kcms/detail/61.1450.TP.20170801.1551.036.html

