一种求解配电网多阶段规划的改进遗传膜算法*

刘洋，李逐云，雷霞，张晓华，刘增庆，邱少引

（1.国网四川省供电公司发展策划部，成都610041；2.西华大学流体及动力机械教育部重点实验室，成都610039；3.广岛工业大学情报学部，日本广岛）

0 引 言

随着环境的恶化和资源的枯竭，低碳环保、安装灵活的分布式电源（Distributed Generation，DG）在配电网中的接入量越来越大［1-2］。当进行配电网规划时，不同的DG接入位置和容量会影响网架规划，而不同的网架结构也影响DG的选址定容结果，为达到整体最优，常需要将DG和配电网网架统一进行规划［3-4］。另一方面，对于中长期规划，由于其周期长，若采用单阶段的规划模型则难以顾及未来负荷需求和DG接入量的改变，故有必要将规划分为几个时间段进行，即运用多阶段规划方法，根据负荷的发展动态地投入电气设备，以得到整个规划周期内最佳的方案［5］。电网规划是离散、非线性、多变量的复杂优化问题，对其计算求解十分复杂甚至困难，目前国内外专家学者就规划算法进行了大量研究。文献［6］在求解配电网规划中将模拟退火和禁忌搜索算法结合到遗传算法中，形成改进混合遗传算法，防止了算法早熟现象。文献［7］采用遗传算法完成了对配电网扩展规划模型的求解。文献［8］在粒子群算法中加入混沌扰动，有效求解出含DG的配电网规划问题。对于多阶段且考虑DG选址定容的配电网规划问题，其涉及的变量更多，求解难度更大，经典的数学优化算法易陷入“维数灾”［9］，大多都做了一定简化，虽能提高求解效率但求出的只是一定意义上的局部最优解。现代智能算法（如遗传算法）可不用调整目标函数和约束条件，但其传统的编码方式、随机产生初始解的大量不可行性和进化规则的局限性，限制了算法搜索的可行区域，导致其进化速度慢，全局收索能力较弱。新型膜计算［10］提供了较好的计算模型，并含有大量的运行机制，将遗传算法引入到膜计算中，组合成进化规则更丰富的遗传膜算法（Genetic Membrane Algorithm，GMA）［11］，可得到较遗传算法更好的收敛能力。然而，在GMA的交叉和变异操作中，交叉和变异概率均为固定值，这较难客观反映进化中各个解对象在不同时期的不同要求，从而在一定程度上影响了算法收敛精度和收敛速度以至阻碍了算法的推广应用。因此，需要进一步研究算法的编码、初始解产生和进化规则等多方面的改进以实现配电网多阶段规划的有效求解。

基于上述分析，本文考虑DG选址定容和配电网网架扩展的统一规划，首先，建立以计及投资、运维、停电、环保和报废成本的全寿命周期成本（Life Cycle Cost，LCC）现值之和最小为目标的配电网多阶段规划模型，然后，提出以反余切-指数自适应交叉换位、反正切-指数自适应变异改写以及膜间交流重组为进化规则的改进遗传膜算法（Improved Genetic Membrane Algorithm，IGMA）来求解问题。采用有向图的邻接矩阵进行编码，并结合编码形式通过操作节点的入度来生成全部满足网络辐射性和连通性的初始解，同时也可对进化过程中解的不可行情况进行一次性全部修复。最后，通过IEEE 54节点系统验证了所提算法的有效性。

1 配电网多阶段规划模型

1.1 目标函数

综合考虑整个规划周期内发生的所有费用，以全寿命周期成本现值和最小为目标：

式中LCC为规划方案全寿命周期总成本现值之和；N、n分别为规划的阶段数和第 n个阶段；CIn，L为第n阶段新建线路的投资成本；CIn，DG为第n阶段新建DG的投资成本；COn为第n阶段系统的运行年成本（主要考虑的是网损费用）；CMn为第n阶段线路的维护年成本；CFn为第n阶段系统的停电损失年费用（主要指线路故障导致的停电损失费用）；CDGn为第n阶段DG的运维年成本；CEn为第n阶段减排污染物的环保年效益；CDn为第n阶段末期的报废成本；δ1=1/（1+r）d（n）为第 n阶段的投资折现系数，d（n）为第n阶段前的年限之和；δ2=（1+r）g（n）-1/r（1+r）e（n）为第n阶段年金折现系数，g（n）为第n阶段包含的年限；e（n）为第n阶段及其以前阶段的年限之和；δ3=1/（1+r）e（n）为第 n阶段末残值折现系数；r为贴现率。

式（1）中各种成本计算如下：

式中 ni为第 n阶段新建线路数；CIL，i、li分别为第i条新建线路的单位长度费用和长度。

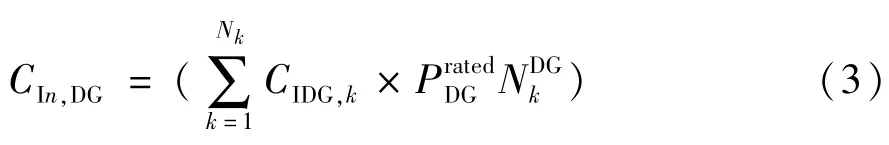
式中 Nk为 DG接入节点数；CIDG，k为单位容量DG投资成本；PratedDG为单台DG的额定功率；NDGk为第k个节点接入DG的台数。

式中 Cpu为电价；Ploss，n为第n阶段最大负荷运行时的网损；τmax，n为第n阶段年最大负荷利用小时数。

式中λL为线路维护费用占初始投资的比例系数。

式中 Nnode，n为第 n阶段网络负荷点数；EENS，i为研究期间第i个负荷点的电量不足期望值；Nb，n为第n阶段网络支路数；λj为第 j条线路的故障率；PENS，i为第j条线路故障引起第i个负荷点的电量不足功率；τENS为故障持续时间。

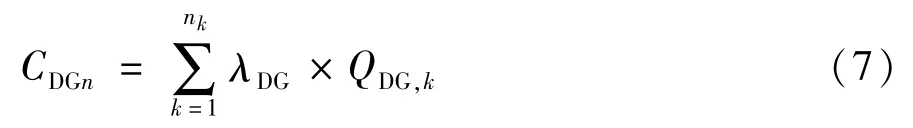
式中 nk为DG总数；λDG为DG单位发电量的运维成本；QDG，k为第k个DG的年发电量。

式中nl为第n阶段燃煤发电产生的污染物数；λ1，l、λ2，l分别为第 l种污染物的排放费用和环境价值；Bn，l为第 l种污染物的排放强度。

报废成本是指设备的残值和报废处置费用，若设备未到使用寿命而要提前拆除可采用直线折旧法计算，若在规划期末到了使用寿命则取为其初始投资的某一比例。

1.2 约束条件

配电网多阶段规划模型存在节点功率平衡、节点电压上下限、支路功率最大限、DG接入容量上限、架线不复拆以及配电网运行的辐射性和连通性等约束条件。

2 配电网多阶段规划模型的IGMA求解

2.1 IGMA的基本原理

膜计算是从生物活细胞以及其组成的器官或组织的结构和功能中类比出的一种计算模型。膜系统主要由膜结构、对象多重集和进化规则三大块组成。膜结构中包含不同层次的膜，每一层膜都有其特定的区域，区域里存放着对象多重集和进化规则，对象多重集可按照膜中的进化规则实现更新进化，从而指导膜的正常运行［10］。

结合遗传算法求解优化问题的特点，把其融入进膜计算的模型中，形成为遗传膜算法（GMA）可实现两者的优势互补。文章在GMA的基础上，将其交叉和变异操作进行改进自适应的变化，使交叉和变异的概率随对象适应度值和迭代次数自行调整，同时还进行了不同膜之间的数据交流传递以及交叉重组，从而构成进化规则更为灵活多样的改进遗传膜算法（IGMA）。同时，针对配电网的规划问题，结合图论知识，本文对算法中解对象编码、初始解的产生和不可行解的修复也进行了改进。

文章提出的IGMA搭建了一个4层膜系统，其形状如图1所示，也可由式（9）说明。

式中V为对象字母表；T为输出字母表；μ为膜结构；ωi、Gi、（o1i，…，oGi）、Ri、ρi分别为膜 i中的解对象集、对象集规模、具体的解对象、进化规则集以及各规则的偏序关系。

图1 IGMA的膜结构Fig.1 Membrane structure of IGMA

2.1.1 解对象编码

传统0-1向量编码在表达网络拓扑信息时需要进行解码工作，网络规模越大则解码工作量越大，进而减缓了整个算法的计算速度。考虑到配电网络实质上是一个由节点和边组成的有向图，本文利用有向图的邻接矩阵表示方法进行解对象的编码，以图2为例，编码结果为矩阵A。A是一个上三角方阵，其元素aij=1表示从节点i到节点j相连接，aij=0表示从节点i到节点j不连接。矩阵A可直接反映某一网络的拓扑信息，故采用邻接矩阵编码方式无需进行解码操作，可增加算法的求解效率，而且非常有助于产生全部可行的初始解和一次性全部修复进化中解的不可行情况（即孤点、孤链和环），无需多次循环操作。

图2 编码示例Fig.2 Example of encoding

为减少存储空间并实现DG和网架规划的同时迭代，可用A的第一列完成对DG的编码，其中每一位元素表示对应节点接入DG的台数。一个矩阵A即表示某一阶段的规划方案，不同阶段的规划方案（多个矩阵A）构成一个元胞数组，此元胞数组即表示整个多阶段的规划方案。

2.2.2 初始解对象产生

在求解过程中若直接随机生成初始解对象集，会产生大量的不可行解，从而占据解空间范围，导致计算效率低下。为提高求解速度，结合上述编码方式本文提出一种通过操作节点的入度使得初始解全部可行的方法。

首先需要说明下述3点：

（1）矩阵A中每列元素的和为对应节点的入度（与节点直接相连的上游节点数）；

（2）为了保证配电网的辐射性和连通性，A的上三角中有且只能有Nb个元素值为1（Nb为网络总支路数），因为若大于Nb，表示支路多了即有环存在；若小于Nb，表示支路少了即有孤点或孤链存在；

（3）除了电源节点外，每个节点的入度只能为1，这是因为若大于1，表示流向此节点的上游节点有多个即有环存在；若小于1，表示此节点没有上游节点即有孤点或孤链存在。

控制节点入度的具体操作过程为：

（1）随机产生一个只由0，1组成且上三角有Nb个元素值为1的方阵A；

（2）求出A中每一列元素之和（节点入度），存于向量B中，并找出入度大于1的节点与入度小于1的节点；

（3）对于入度大于1的节点，找到其所在列值为1的元素，并随机将一些元素的值置0，只保留一个值为1的元素；

（4）对于入度小于1的节点（除电源点），随机将主对角线之上其所在列的某位元素的值置1。

至此，即完成了一个可行解的生成，上述（2）～（4）步即是对不可行情况的全部修复过程，对图2网络的修复过程如图3所示，假设节点1为电源点。

图3 修复不可行解的示例Fig.3 Example of revising an infeasible solution

2.2.3 膜内自适应进化规则

对于基本遗传算法（Simple Genetic Algorithm，SGA），固定不变的控制参数容易导致算法早熟和局部收敛，因此出现了自适应遗传算法。但是，对于标准的自适应遗传算法（Adaptive General Algorithm，AGA），其公式设定了对象适应度值越大则对象交叉概率和变异概率就越小，当等于最大适应度值时，交叉概率和变异概率的值为零，这种设定会导致在进化初期较优对象几乎处于不进化的状态，然而优良对象在此时不一定是优化的全局最优解，于是很可能使得进化走向局部最优。基于此，文章考虑影响交叉和变异概率取值的两重因素—对象适应度值和算法进化代数，提出了反余切-指数自适应交叉换位规则和反正切-指数自适应变异改写规则，让交叉和变异概率依据对象适应度值的大小按指数曲线变化而不再是进行简单的线性变化，这有助于对优良对象的保护和劣质对象的更新，同时，引入反正（余）切进化代数规律避免了交叉和变异概率的骤升骤降，实现了交叉和变异概率在不同的阶段对应不同的取值，从而保证算法进行了局部细致和全局广泛的综合搜索。

（1）反余切-指数自适应交叉换位规则：此规则在膜内进化操作中，首先随机选择交叉换位点，然 后在进化代数上按照反余切规律、在适应度值上按照指数规律去自适应生成交叉概率，最后将满足交叉概率的两个对象的相应位置互换从而生成新对象。规则具体表达如式（10）所示，交叉概率的反余切-指数变化如图4所示。

图4 交叉概率变化Fig.4 Changing of cross probability

（2）反正切-指数自适应变异改写规则：此规则在膜内进化操作中，首先随机选择变异改写点，然后在进化代数上按照反正切规律、适应度值上按照指数规律去自适应生成变异概率，最后将满足变异概率对象的相应位置元素换为其等位元素以得到新对象。规则具体表达如式（11）所示，变异概率的反正切-指数变化如图5所示。

图5 变异概率变化Fig.5 Changing ofmutation probability

由图4和图5可以看出，随着迭代次数的增加，解对象的交叉概率pc逐渐减小、变异概率pm逐渐增大，这样保证了在进化初期，算法以较大的交叉概率和较小的变异概率进行全局搜索，以避免过早收敛，而在进化后期，减小交叉概率增大变异概率，进行局部搜索，重点进化，从而加快收敛速度。另外，在某次迭代过程中，解对象在其适应度值小于对象集平均适应度值时其pc和pm恒定，而适应度值大于平均适应度值时，随着适应度值的增大对象的pc和pm变得越来越小，这可在一定程度上保护当代的优良对象。

2.1.4 膜间交流重组规则

在每代计算完成后，将新对象集按照适应度值高低排序，然后把各膜内适应度值高的某些解对象输送给其他膜，同时也接受其他膜内适应度值高的相应解对象。此外，为了充分利用外界对象的优良基因，算法中设定交流对象具有更高的交叉概率，以将外膜对象的优良基因在本膜内传递下去。交流重组规则可完成不同膜之间的数据互换以及基因遗传，从而可增大对象集的多样性，提高算法的全局搜索能力。规则具体表达如下：

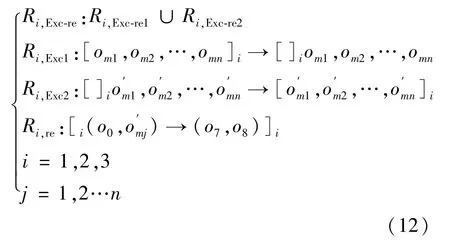
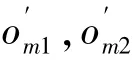
2.2 IGMA求解流程图

IGMA算法求解配电网多阶段规划模型的流程如图6所示。

图6 计算流程图Fig.6 Calculation flow chart

3 算例分析

3.1 参数设置

采用IEEE 54节点系统［12］为算例进行分析，初始网络如图 7所示，其中 S1、S2、S3、S4为已有变电站，实线为已有线路，虚线为待新建线路。根据负荷预测结果将规划分为3个阶段，每阶段年限为5年，其中节点 26、27、43、49、50为第二阶段新增负荷，节点35、38为第三阶段新增负荷，系统的节点和线路数据详见文献［12］附录C。

图7 初始网络Fig.7 Initial network

其他数据：电价为0.4元/kWh；最大负荷利用时间为3 000 h；折现率为0.1；线路维护成本取为初始投资的3%；线路平均残值取为其初始投资的2%；假设在节点5、8、9、10、33可接入分布式光伏发电，光伏发电机接入最大台数均为10台，单台容量100 kW，功率因数0.9，投资费用取10 000元/kW，运行维护费用取0.2元/kWh；传统燃煤发电产生的NOx、SO2和CO2的排放强度分别为1.634 kg/MWh、4.445 kg/MWh和1 008.788 kg/MWh，排放费用分别为2元/kg、1.26元/kg和0.765元/kg，环境价值分别为8元/kg、6元/kg和0.023元/kg。

3.2 规划结果分析

对系统进行多阶段规划，结果如图8所示。图中黑色三角形表示DG接入，黑色加粗线表示每阶段的新增线路。由图8可看出每个阶段的规划结果均满足网络辐射性和连通性约束；另外，每个阶段新增的线路在可选新建线路集中均尽量建设在原有较短供电路径上（例如第3阶段中节点35接在了节点36上而未与原路径较长的节点34连接），这样避免了单条供电路径过长导致网损增大、节点电压降低的情况，保证了电网运行的安全性和经济性。

不考虑负荷的动态变化，采用所提IGMA算法进行系统的单阶段规划，其结果与多阶段结果的比较如表1所示。

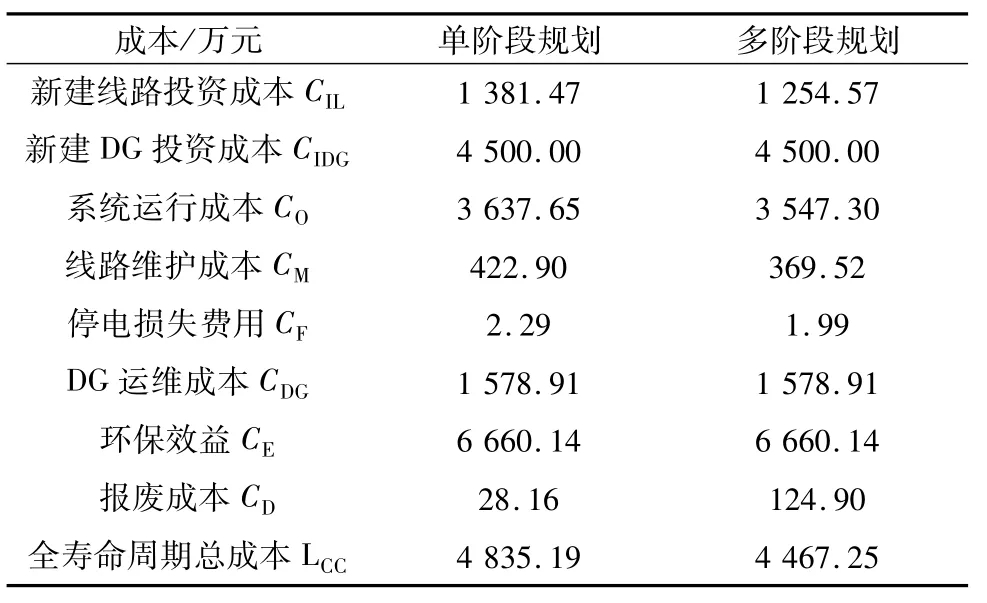
表1 单阶段和多阶段规划比较Tab.1 Comparison of single-stage and multi-stage planning

图8 配电网多阶段规划结果Fig.8 Result of multi-stage planning of distribution network

由表1可看出，多阶段规划方案在规划周期上的总成本值小于直接单阶段规划的总成本值，说明多阶段规划不仅可满足负荷的动态变化，而且能在合适的时间上安排设备的建设，合理分配设备的投资，具有更好的灵活性和经济性。

本文的配电网规划模型同时考虑了DG的选址定容和网架的扩展，故算例中也采用IGMA算法进行了DG和网架的分开独立规划，两种规划方法的结果（以第一阶段为例）比较如表2所示。

表2 独立和统一规划比较Tab.2 Comparison of independent and coordinated planning

由表2可看出，在运行费用、停电损失和总成本上，进行DG和网架的统一规划均小于两者的独立规划，这说明在配电网规划时，统一考虑DG和网架的规划可促进两者的相互作用，减少系统损耗，提高系统可靠性。另外，DG和网架统一规划中在节点5、8、9、10、33分别接入了 7台、10台、10台、8台、10台DG，而独立规划中仅在节点5、8、9、10分别接入了6台、8台、7台、6台DG，这说明在电网安全运行的约束条件下，进行独立规划允许接入电网的DG容量较小，即不能充分挖掘电网对DG的接纳能力。

3.3 算法性能分析

为了说明所提IGMA的高效性，算例中采用了IGMA、GMA和SGA去求解所建模型，将三种算法的求解结果进行对比，可得算法的计算时间如表3所示，算法的收敛情况如图9所示。此外，还对三种算法分别独立进行了50次计算，以统计算法稳定性，其结果如图10所示。

表3 计算时间比较Tab.3 Comparison of calculation time

从表3可以得出，SGA、GMA、IGMA三种算法的运行时间依次增大，这是因为GMA和IGMA增加了一定数量的进化规则，所以导致了算法运行时间的加长。然而，对于离线的配电网规划问题，在一定程度上以牺牲计算时间从而设计更好的优化方案是可行的。

图9 算法收敛图Fig.9 Convergence of algorithms

图10 算法稳定性测试曲线Fig.10 Stability testing curves of algorithms

由图9可发现，SGA、GMA分别在近第37次和第48次迭代时便陷入局部最优中且很难跳出，而IGMA在第23代达到收敛且收敛值均优于GMA和SGA，故所提IGMA算法较其他两种算法具有更强的寻优能力和更快的收敛速度。

由图10可以看出，针对配电网多阶段规划问题，GMA的不收敛次数有12次，SGA有7次，而IGMA只有4次，经计算可知SGA的稳定性为86%，GMA为76%，IGMA为92%，说明GMA在SGA基础上仅增加膜间的运行规则虽可提升算法的寻优能力但却降低了其稳定性，而IGMA因在膜间运行规则和膜内遗传操作上均进行了改进，故其能够在提升全局搜索能力的条件下保证算法的稳定性。

4 结束语

文章在配电网接入DG的背景下，考虑负荷的动态变化，采用多阶段规划方法进行了DG的选址定容和配电网网架的扩展规划。提出一种改进遗传膜算法用以求解此问题，并采用有向图的邻接矩阵进行初始解对象的编码，和通过操作节点的入度来保证计算过程中所有解的可行性。最后，通过算例表明：

（1）多阶段规划根据负荷的发展，在适宜的时段投入相关的电气设备，能够体现规划的动态性，并具有更佳的经济性；

（2）在配电网中统一进行DG和网架的规划，可提高电网对DG的接纳能力，减少系统网损，增大可靠性，提高环保性；

（3）IGMA算法较GMA和SGA而言具有更强的寻优能力，更快的收敛速度和更高的计算稳定性；

（4）结合有向图的邻接矩阵编码方式，通过操作节点入度，可实现一次修复解的各种不可行情况。