基于残差补偿灰色马尔科夫模型的校准间隔预测方法*

纪伊琳，钱政

（北京航空航天大学仪器科学与光电工程学院，北京100191）

0 引 言

测量仪器受各种外界环境因素和内部元器件老化的影响，准确度会随着仪器使用时间的延长而逐渐降低，经过一段时间就会降低到难以满足预期使用要求的程度。为确保仪器的准确度符合使用的要求，通常要求按照国家标准中规定的时间间隔对测量仪器进行校准。连续两次校准的时间间隔定义为校准间隔。通过对电子仪器计量校准情况的调查，我们发现几乎所有的电子仪器校准间隔均为一年。实际上，部分电子仪器使用频率低、环境良好，且连续多年校准结果均未超差，该部分仪器的校准间隔完全可以适当延长；而部分电子测量仪器由于使用环境恶劣，且工作时间长、频率高，其量值特性参数变化较大，容易出现超差情况，相应地校准间隔应该有所缩短。因此，将校准间隔统一规定为某一固定值并不合理。无论是校准间隔过短或者过长，都会带来诸多问题。校准间隔选取过短，将导致仪器使用成本的上升，并降低仪器的使用效率；校准间隔选取过长，仪器在超出允许误差限的情况下使用的风险将会加大［1］。因此，根据仪器的历史数据和实际使用情况来进行校准间隔的预测，能够很大程度地避免上述问题，具有重要的工程应用前景。

国际和国家标准均提出应根据仪器的自身特征、性能要求和使用情况来确定其校准周期［2-3］，以提高校准工作的效率。由于实际情况存在巨大的差异，文件中并未明确规定校准间隔确定的详细步骤，仅给出几个备选的方法，因此如何确定校准间隔仍有待进一步的研究［4-5］。确定校准间隔的方法，通常是通过对历史数据建模（包括统计模型和非统计模型），推断数据未来的发展变化趋势，判断其是否落在合格区间内，进而得到校准间隔的预测值。其中，统计模型的建立要求掌握与待校准仪器同一型号的多台设备的历史校准数据，并且只在仪器可靠性的变化符合指定模型的时候才能得到比较准确的校准结果。然而，实际的校准数据（尤其在校准初期）很难满足上述的条件［6］，通常只能获得少数同型号仪器在某些年份的历史数据。文献［7］采用灰色GM（1，1）模型对历史校准数据进行处理和建模，从而预测出测量设备失效和需要校准的时间，实现对其质量的管理和控制。然而，一旦校准数据出现较大的波动性，GM（1，1）模型的预测准确度就会下降，表现为预测结果的残差较大。

鉴于灰色理论以具有“小样本”、“贫信息”特点的不确定性系统为研究对象［8］，本文采用灰色GM（1，1）模型预测校准数据的总体发展趋势，求得真实值与预测值之间的残差，继而采用马尔科夫状态转移矩阵预测残差在总体趋势下的未来状态变化，从而建立基于残差补偿的灰色马尔科夫预测模型，给出了校准间隔预测的具体步骤，使方法的有效性得到实例验证。

1 建模思想

测量设备的校准数据是多种因素共同作用的结果，其中某些因素起到主导作用，另一部分因素对结果产生不稳定的影响。因此，可以把测量设备的历史校准数据序列分成具有确定性的趋势项和具有波动性的随机项［9］。其中，趋势项表征了设备本身固有的特性和使用条件等因素导致的稳定、长期的发展态势；随机项则表征了导致数据偏离稳定发展趋势的各种随机扰动。两者性质不同，故本文采用不同的方法进行建模和预测，以求可以达到较高的准确度。

测量设备的校准周期比较长，通常以年为单位，因此导致了校准数据量非常有限，对数据量要求较大的算法，如神经网络等，并不适用于这种情况。而灰色系统理论恰好适用于小样本的研究对象，因此本文采用GM（1，1）模型对历史校准数据进行预测，得到其总体发展趋势。受各种随机因素的影响，GM（1，1）模型的预测值会出现一定程度的偏差。本文求出GM（1，1）模型拟合原始数据的残差，通过马尔科夫预测模型对残差进行合理的状态划分，用状态转移矩阵预测状态的发展变化，能够弥补灰色模型的不足，以较高的准确度获得随机项的预测结果。两者结合可以优势互补（如图1所示），实现对电子设备校准间隔的科学预测，从而起到辅助决策的作用。

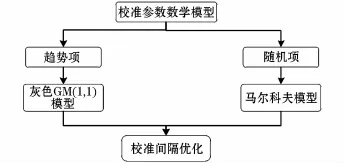
图1 灰色马尔科夫预测模型Fig.1 Grey-Markov prediction model

2 残差补偿灰色马尔科夫预测模型

2.1 灰色 GM（1，1）模型建模

残差补偿灰色马尔科夫预测模型的建立先要依据灰色理论，对校准数据进行建模。灰色GM（1，1）预测模型的建模机理如下所述［10］。

假定包含n个采样数据的原始数据序列为：

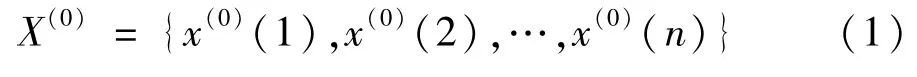
经过一次累加生成后数据序列变成：

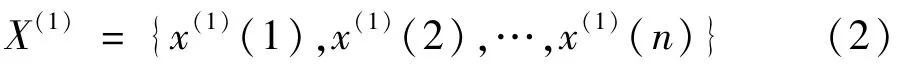
称 x（0）（k）+ax（1）（k）=b为 GM（1，1）模型的原始形式。其中 a是发展系数，a，b是微分方程的参数。

对参数a，b的估计如下：

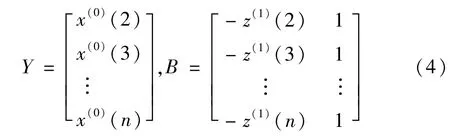
对 X（1）作紧邻域生成，得到：

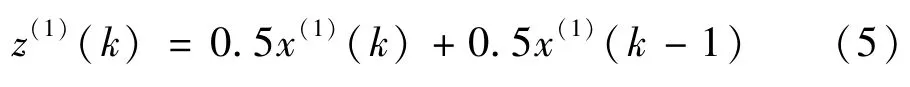
依据灰色理论建立一阶微分方程：

该方程的解即为X（1）的预测值。

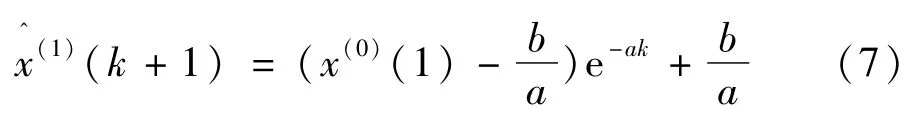
对式（7）做累减生成，可得到还原值：

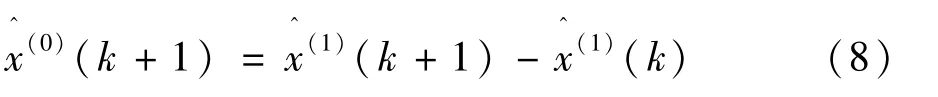
这样，我们就得到了历史数据的灰色预测模型。不可避免地，历史数据中包含的随机因素（如环境因素）也被加入到模型中，进而对灰色预测模型的准确性造成了负面影响。

比较灰色预测模型的预测数据与真实的历史数据，可以看到预测数据具有发展平稳的特点，而历史数据则具有较明显的波动特征。由于随机因素的影响就是使校准数据呈现出波动性的特征，因此，可以将预测数据与历史数据之间的残差作为随机项的表征，用马尔科夫对残差进行状态划分和预测，进而弥补灰色预测模型的不足。

2.2 残差的马尔科夫状态预测

残差即校准数据中的随机项，定义为真实值与预测值的差值，是符合马尔科夫链特点的非平稳随机序列，表征了校准数据中随机因素的影响，因此可以依据马尔科夫理论进行状态划分和状态预测。

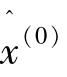
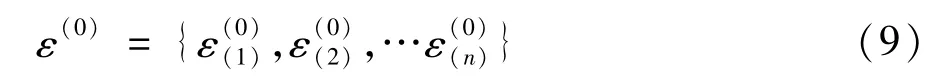
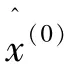
在马尔科夫模型的建立中，如何对数据进行状态的划分是一个难点，对模型的预测效果有很大的影响。状态的划分包括状态数量和状态区间上下限的确定，如果状态划分不合理，将严重影响预测结果的准确度，难以得到可靠的预测值。现有的状态划分往往是依据数据的分布情况人为确定的。为了科学合理地划分不同的状态，本文采用了如下的步骤。

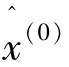
根据马尔科夫模型，数据序列由状态Ei，经过k步转移之后到状态Ej的概率称为k步转移概率pij（k）。当 k=1，就是一步状态转移概率 pij。假设根据样本资料可知状态Ei出现的次数为mi，由状态Ei转移到状态 Ej的次数为 mij，则一步状态转移概率为：

如果把系统所有的一步状态转移概率构造成一个矩阵，那么这个矩阵就叫做一步转移概率矩阵。表达式如下：

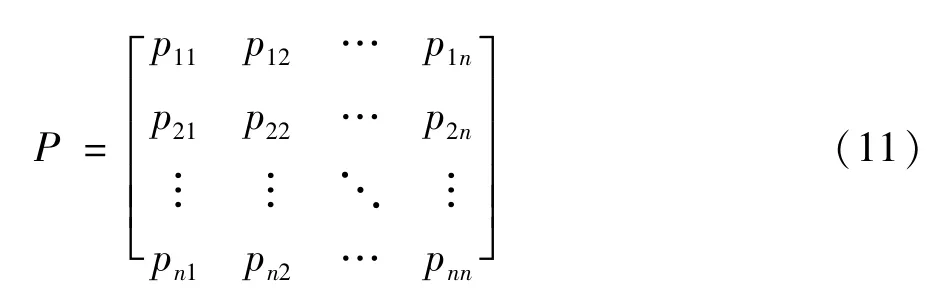
前文根据测量仪器校准数据的特点，将数据划分为四个状态，因此，一步转移概率矩阵应为四阶方阵。由于已经确定了残差序列中各个元素对应的状态，统计序列中ε（0）各个状态转移的具体频数，用式（10）计算状态转移概率，可得一步状态转移矩阵P：

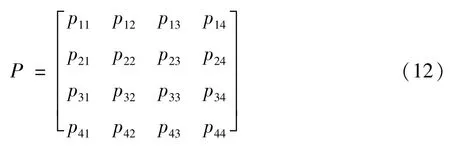
假设初始状态向量s0，根据马尔科夫预测模型，s1=s0P，s2=s0P2，…，sn=s0Pn，可以得到预测状态向量。根据预测状态向量中的最大值，判断残差转移后最有可能的状态Ei，随机项预测结果最可能为状态Ei对应区间的中位数：

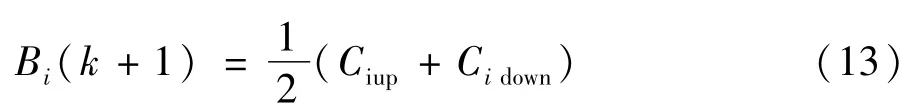
式中Ciup为状态Ei对应区间的上限；Cidown为区间的下限。

2.3 残差补偿灰色马尔科夫预测模型

以上完成了模型的趋势项和随机项的估计，计算两者的代数和，则最终的估计结果为：

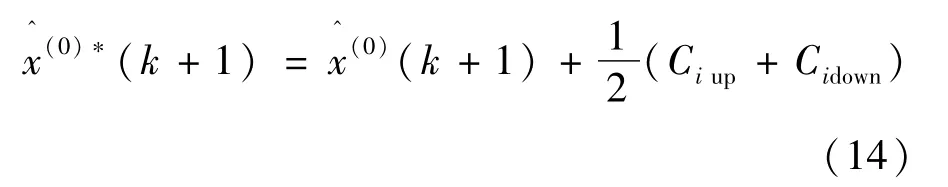
随着时间的推移，影响系统的随机因素可能发生改变，因此，依据历史数据建立的预测模型只对紧随其后的几个数据有较高的预测准确度。实际应用中，可以考虑舍弃距离当前时刻较远的历史数据，并将新信息加入模型进行预测，以获得较准确的预测结果。

3 仿真实验与结果分析

在某电子测量设备校准间隔确定方法研究项目中，为了确定科学合理的校准间隔，项目对美国某公司的型号为Fluke45的数字万用表进行了长期监测，得到了能反映测量设备性能的关键参数的校准值。本文对这部分数据进行研究，通过对历史数据建立模型来预测其后续的发展变化是否超出合格范围的上下限，进而判断未来的一段时间内校准间隔是否需要进行调整。这部分数据如表1所示。

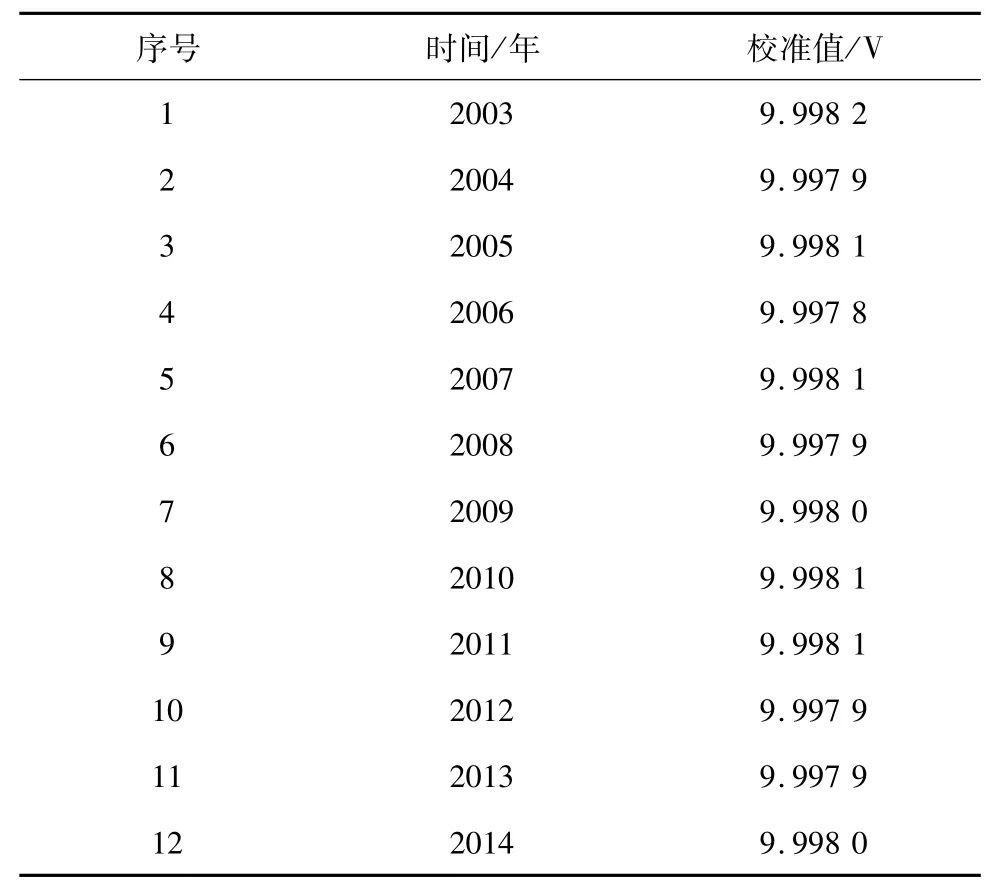
表1 Fluke45的历史校准数据Tab.1 Historical calibration data of Fluke45

给定10 V电压作为标准值校准数字万用表，根据数字万用表的校准规程，如果作为关键参数的电压校准值落在区间［9.98，10.02］内，则表示校准结果合格。将数字万用表Fluke45的校准值作为原始数据序列，分别用灰色GM（1，1）模型和残差补偿灰色马尔科夫模型对数据进行处理，得到的结果如图2和图3所示。

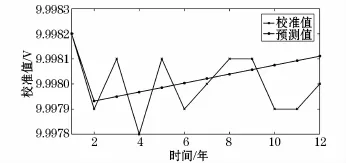
图2 灰色GM（1，1）模型的预测结果Fig.2 Prediction results of GM（1，1）model

从图2中可以看出，灰色GM（1，1）模型很好地跟随了关键参数的发展趋势。比较灰色预测模型的预测数据与真实的历史数据，可以看到预测数据具有发展平稳的特点，而历史数据则具有较明显的波动特征。由于随机因素的影响正是使校准数据呈现出波动性的特征，可以得知现有的灰色预测模型仍不能体现出随机因素对校准数据的影响。

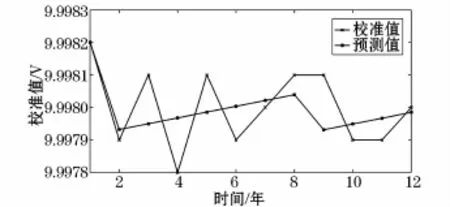
图3 残差补偿灰色马尔科夫模型的预测结果Fig.3 Prediction results of residual compensation Grey-Markovmodel

因此，可以将预测数据与历史数据之间的残差作为随机项的表征，用马尔科夫对残差进行状态划分和预测，进而弥补灰色预测模型的不足。图3给出了残差补偿灰色马尔科夫预测模型的预测结果，预测结果的前八个点没有引入马尔科夫预测模型的修正，其结果与图2相同；随后四个点引入了马尔科夫预测模型对残差的状态进行预测，进而修正原有的预测值。

表2给出了2011年～2014年两个模型预测结果的相对误差，其中，模型1和模型2分别是灰色GM（1，1）模型和残差补偿灰色马尔科夫预测模型。对比两个模型的相对误差，可以看出，加入残差补偿的模型具有更高的预测精度，相对误差明显小于单纯的灰色 GM（1，1）模型。

表2 灰色GM（1，1）模型与残差补偿灰色马尔科夫模型预测结果对比Tab.2 Comparison of prediction results of GM（1，1）model and residual compensation Grey-Markov model

因此，可以得出以下结论：修正后的模型可以反映随机波动项的变化，其拟合值更接近真实的校准结果，相比灰色GM（1，1）模型具有更高的准确度。建立残差补偿灰色马尔科夫预测模型对校准值进行预测，可以看出数字万用表的电压校准值在未来两年不会超出合格区间［9.98，10.02］，因此，这段时间内可以不对数字万用表进行校准，校准间隔可以适当延长。

在校准数据较少的情况下，残差灰色马尔科夫预测模型除了预测数据总体的走向，还体现了残差随机变化的过程，灰色预测与马尔科夫预测的结合很好地反映了测量仪器关键参数的发展过程，适于校准间隔的预测与优化。

4 结束语

文章基于灰色预测和马尔科夫预测的各自优势，采用灰色GM（1，1）模型预测校准数据的总体趋势，求得残差后利用马尔科夫模型分析残差的状态转移过程，将随机因素的影响加入预测模型中，使得模型在数据受到波动性较大的随机因素影响的情况下仍有较好的预测能力，提高了模型的预测准确度。

实际校准数据表明，残差补偿灰色马尔科夫模型可以有效预测测量仪器关键参数随时间的发展和变化，实现校准间隔的预测，有效地避免校准间隔选取不合理的问题，提高校准工作的效率。