基于空间矢量的快速电压暂降检测方法*

程志友，马千里，张红飞，李涛

（1.教育部电能质量工程研究中心，合肥230039；2.安徽大学 电子信息工程学院，合肥230039；3.国家电网安徽培训中心，合肥230051）

0 引 言

电压暂降是指供电电压有效值在短时间内突然下降的事件，其典型持续时间为0.5～30个周波。国际电气与电子工程师协会（IEEE）将其定义为电压有效值下降到额定值的90%～10%［1］。工业生产和民用产品中的各种电气设备，如PLC控制器、继电器以及各种数字计算机等，对电压暂降都相当敏感，电压暂降会导致其运行故障，从而造成大量的经济损失。输电线路短路故障和大功率装置的启动以及恶劣气候条件是引起电压暂降的主要原因［2］。

国内学者对电压暂降的检测和特征分析做了大量的研究［3-7］。一般情况下，电压暂降可分为A～G七种类型［8］，必须分别检测出暂降类型并采取相应的处理措施，才能确保电力系统的稳定运行。常用的电压暂降检测方法有直接检测法（如有效值检测法、峰值电压检测法）、基于变换的方法（如dq变换、S变换等）和基于分解的方法（如傅里叶分解、小波分解）等。这些方法存在着不同的优势和不足之处［9］。文献［10］提出了一种基于同步旋转坐标系的电压暂降方法，通过对单相电压信号进行微分处理，结合αβ-dq变换构造出电压暂降信号，检测速度较快，但在对电压信号进行微分处理的同时，原始电压信号中的噪声将被放大，从而影响检测精度。文献［11］提出了一种基于小波变换和人工神经网络的电能质量扰动检测和分类方法，该方法需要进行大量的小波变换计算和大量已有数据的支持，从而导致实时性不强。Padmanabh Thakur等人在文献［12］中提出了一种基于电压特性和电压零序分量的电压暂降类型检测和分类方法，通过引入两个电压指标来判别不同的电压暂降类型，由于该方法使用了均方根电压值进行数据计算和分析，从而导致时间滞后。

Vanya Ignatova等在文献［13］中提出了一种基于空间矢量的电压暂降与电压暂升分类方法，使用三相电压椭圆参数进行电压暂降与暂升的分类，但在分析过程中没有考虑电压暂降发生时伴随相位角跳变的情况，并且需要一个周期的三相电压信号数据，应用范围较窄。本文作者深入研究了电压暂降中伴随单相电压相位角跳变的情况，同时结合快速的椭圆重构算法，提取电压暂降故障时间内三个不同时间点的三相电压数据，即可重构出空间矢量在复平面上的轨迹。由该轨迹检测电压暂降的发生同时判断出故障相，并使用椭圆参数求解出电压相位角跳变值，然后根据该值对故障相电压数据进行移相处理，最终由处理后的数据可以快速计算出电压暂降深度。

1 电压空间矢量和椭圆重构方法

1.1 电压空间矢量

一个理想的供电系统要求其三相交流电源对称平衡，并且系统负荷特性与电压水平无关。在电压暂降故障之中单相电压暂降是最为普遍的情况，电压暂降发生时，不仅会出现电压幅值跌落的情况，往往还会伴随着电压相位角发生跳变。假设某系统中C相电压发生电压暂降故障，系统三相电压信号如式（1）表示：

其中，U为系统电压有效值；ω为系统角频率；d为电压暂降深度（0.1≤d≤0.9）；θ为电压相位角跳变值。

如图1所示，Clarke Transform将三相电压瞬时量变换到二维平面上静止且正交的αβ坐标系中。

图1可由式（2）表示。

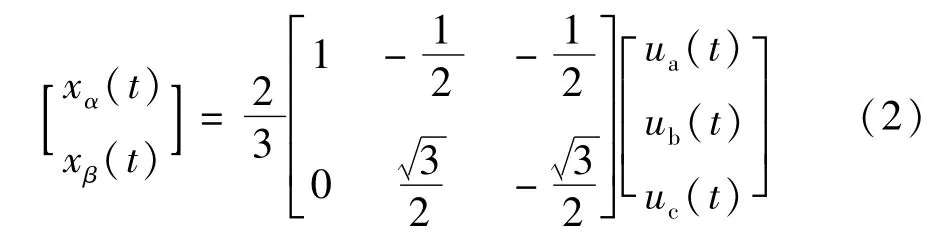
式（2）的矢量表达式为：

图1 Clarke Transform示意图Fig.1 Schematic diagram of Clarke Transform

Euler’s Formula可以将一个正弦量的表达式转换为两个共轭矢量之和［14］，例如：

假设在电压暂降发生前后三相电压的基波和谐波分量均为正弦量，由式（2）、式（3）和式（4），空间矢量表达式可被重构为：

式（5）中，E+=|E+|ejφ+，E-=|E-|ejφ-。由式（5）可知，空间矢量在复平面的轨迹由正交的两个旋转分量E+和E-的模值和初始相角决定。理想情况下，空间矢量在αβ坐标系上的轨迹是一个半径为系统标准电压的圆。在发生三相不平衡电压暂降时，式（6）中的正负旋转分量的幅值会发生变化，空间矢量在αβ坐标系上的轨迹由一个标准圆变为一个椭圆。该椭圆的参数：长半径（Ama），短半径（Ami）和倾斜角（φ）的计算公式如下［15］：

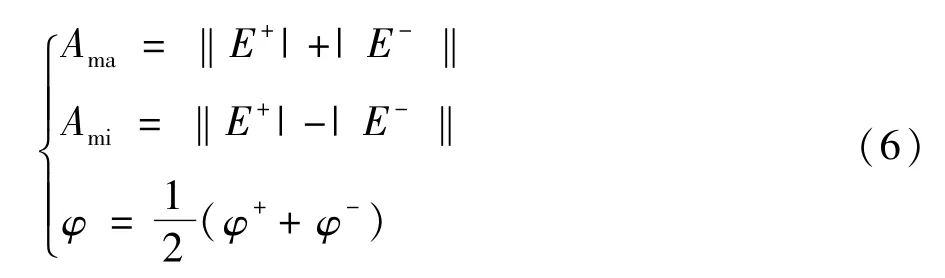
1.2 椭圆快速重构算法

WeiWen和Baozong Yuan在文献［16］中提出了一种鲁棒的椭圆重构算法。该算法仅需椭圆上的若干个坐标点，即可计算出椭圆的方程。

如图2所示。

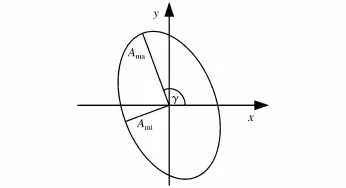
图2 椭圆示意图Fig.2 Schematic diagram of ellipse

当一个椭圆的中心位于坐标系原点时，该椭圆的方程表达式可写为：

图2中：

其中，Ama和Ami分别为椭圆的长半径和短半径，γ为椭圆的倾斜角。假设 P1（x1，y1）、P2（x2，y2）和 P3（x3，y3）是椭圆上的任意三个不同的坐标点，由于椭圆上的所有坐标点都满足式（7），所以通过求解方程组的形式可以快速求出椭圆的表达式。求解如下：

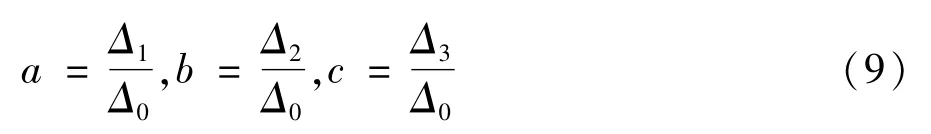
其中：

椭圆的三个参数（长半径、短半径和倾斜角）可由式（11）求出。

2 基于空间矢量的快速电压暂降检测方法

由式（5）可知，当发生电压暂降故障时，空间矢量在αβ坐标系上的轨迹为一个椭圆。文献［17］中给出了单相电压暂降过程中椭圆参数和暂降深度的关系，如式（12）所示：

式中Um表示标准电压峰值；Uf表示故障相的残压值。式（12）中的三种类型电压暂降并未伴随相位角跳变；在伴随相位角跳变的情况下，式（12）中的椭圆长半径和短半径不再适用于计算故障相的残压值，而椭圆倾斜角依然是适用的。在这种情况下，首先由空间矢量在αβ坐标系上的椭圆轨迹得到三个椭圆参数，进而通过求解由式（5）和式（6）构成的方程组来计算出相位角跳变值。方程组如式（13）所示。

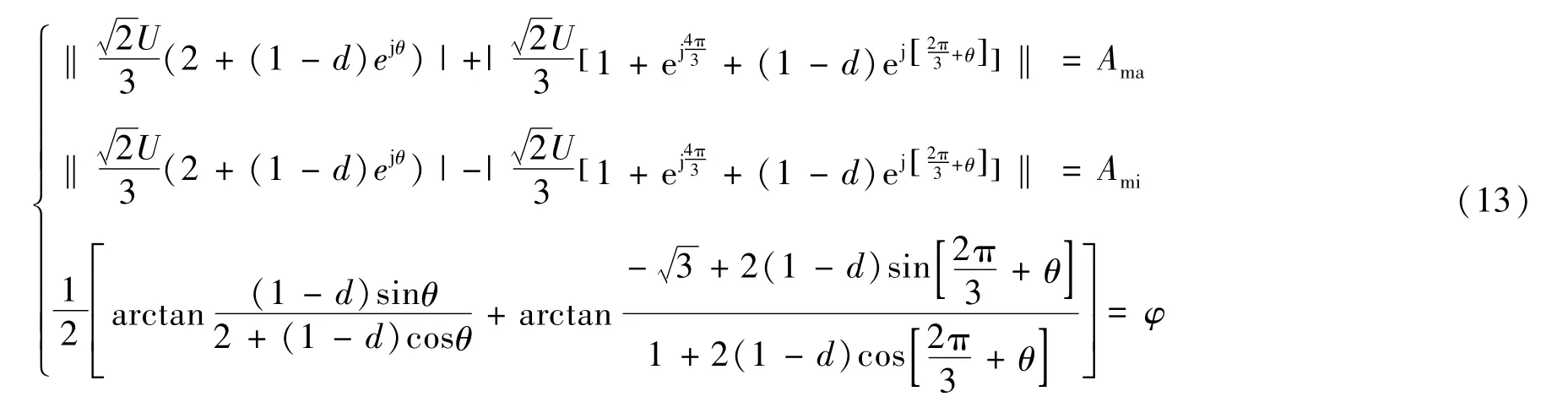
在计算出电压相位角跳变值之后，根据故障相电压的相位角跳变值θ对原始电压数据进行移相处理，此时相当于系统仅发生了电压暂降故障，并未伴随电压相位角跳变。在重新构造三相电压信号后，计算出新的椭圆参数。新的椭圆参数是适用于式（12）的，从而可以快速求解出电压暂降深度。

综上，得出基于空间矢量的快速电压暂降检测方法步骤如下：

Step1：提取一个电压周期内三个时刻的三相电压信号；

Step2：对三个离散的电压信号分别进行Clarke Transform，通过椭圆重构算法计算出空间矢量轨迹方程；

Step3：若轨迹为一个半径为标准电压的圆，即未发生电压暂降；

Step4：若轨迹为椭圆，由椭圆倾斜角确定电压暂降类型；

Step5：由椭圆参数求解方程组，计算出相位角跳变值；

Step6：根据相位角跳变值，对故障相电压信号进行移相处理；

Step7：重构空间矢量，重绘出空间矢量轨迹；

Step8：由式（12）计算出故障相残压值。

3 仿真分析

3.1 理论仿真

为了对本文算法进行验证，下面模拟电压暂降信号。模拟0 s～0.02 s内C相电压发生深度为0.5 p.u.的电压暂降且伴随5°相位跳变的电压暂降故障，构造三相电压信号为：

将这三个矢量的坐标带入式（10）和式（11），求解出椭圆的长半径为 311.357 2，短半径为206.870 2，倾斜角为152.978 5°。空间矢量在复平面上的轨迹如图3所示。

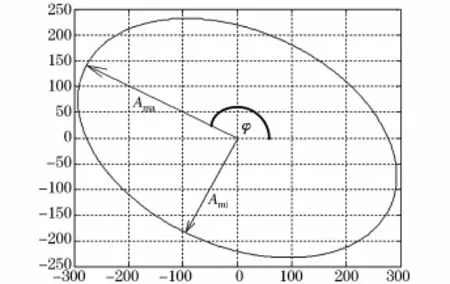
图3 空间矢量轨迹Fig.3 Trajectory of the space vector

首先由椭圆倾斜角快速确定出C相电压发生了电压暂降故障，将椭圆长半径、短半径和倾斜角参数代入式（13），求解方程组得C相电压相位角跳变值为5.001 9°。进而对式（14）中的C相电压进行大小为5.001 9°的移相处理，重构出三相电压空间矢量及其椭圆轨迹，新的椭圆轨迹如图4所示。

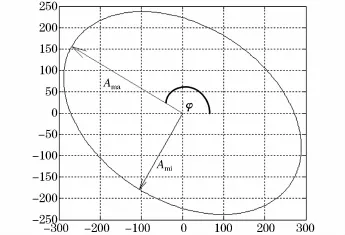
图4 重构的空间矢量轨迹Fig.4 Trajectory of the reconstructed space vector

同理，由重构的三相电压数据可得 Ama为311.127，Ami为 207.428 4，φ为 150°。代入式（6），计算出Uf=155.594 6=0.500 1 p.u.，即C相电压残压值为0.500 1 p.u.，暂降深度d=0.499 9。相对误差δ=0.02%，满足实际电压暂降检测要求。

3.2 电路系统仿真

基于上述理论分析结果，下面通过搭建MATLAB/Simulink电压暂降模型对本文方法继续进行验证。仿真模型如图5所示，系统运行时长为0 s～0.2 s（10个电压周期）。设置三相电源相间电压380V，频率50 Hz，内阻0.3Ω，电感0.006 63 H，中性点接地；传输线路Line的长度为50 km；三相并联负载为恒功率模型；三相故障发生器在0.06 s～0.14 s内发生C相接地短路故障，故障电阻1Ω，接地电阻0.001 Ω，缓冲电阻106Ω，缓冲电容无穷大。

测量点三相电压波形如图6所示。

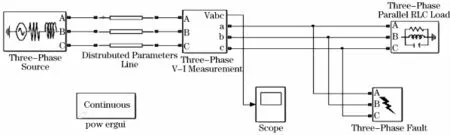
图5 仿真模型Fig.5 Simulation model

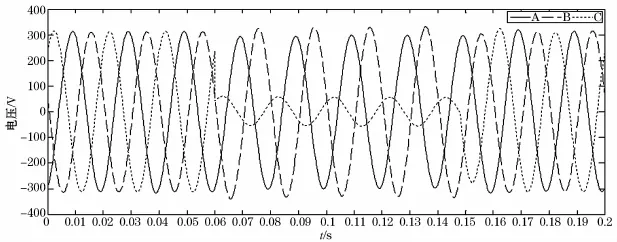
图6 测量点三相电压波形Fig.6 Three-phase voltage waveform of measurement point

由图6可以看出：在0 s～0.06 s内，ABC三相电压值稳定在312.82 V；在0.06 s～0.14 s内，C相电压发生接地短路故障，C相电压急剧跌落，同时A相和B相电压波动；0.14 s时刻接地短路故障结束，故障结束后ABC三相电压很快回到了初始值。

提取0.08 s、0.085 s和0.09 s三个时刻的三相电压数据进行分析，数据如表1所示。

表1 0.08 s、0.085 s和0.09 s三相电压值Tab.1 Three-phase voltage of 0.08 s，0.085 s and 0.09 s

对这三个时刻的电压数据分别进行Clarke Transform，得到三个空间矢量为：

将这三个空间矢量的坐标代入到椭圆重构算法中，计算得：椭圆长半径为 318.656 3，短半径为127.051 6，倾斜角为144.8°。其故障椭圆轨迹如图7所示。

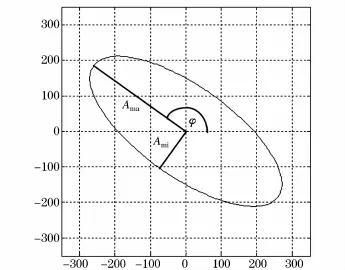
图7 故障椭圆轨迹Fig.7 Fault ellipse trajectory

首先由椭圆倾斜角确定系统C相电压发生了电压暂降故障，然后将椭圆的长半径、半径和倾斜角三个参数代入式（6），求解出θ=3.77°，即C相电压在电压暂降发生时的相位角跳变值是3.77°。

进而对C相电压数据进行大小为3.77°的移相处理，处理后的数据相当于仅发生了电压暂降并未伴随电压相位角跳变，处理后0.08 s、0.085 s和0.09 s时刻的C相电压值为：17.733 7 V、29.846 6 V和-2.354 5 V。然后重构三相电压空间矢量，得到新的空间矢量为：

新的椭圆轨迹长半径Ama为316.25，短半径Ami为128.74，倾斜角φ为145.7°。由式（13）确定系统中C相电压发生了深度为0.889 p.u.的电压暂降故障，且故障发生时伴随大小为3.77°的电压相位角跳变。

4 结束语

通过将三相电压信号进行Clarke Transform，结合快速椭圆重构算法，仅需三个时刻的三相电压数据即可重构出空间矢量的轨迹方程。根据空间矢量在复平面上的轨迹进行电压暂降的检测，在通过椭圆参数计算出单相电压相位角跳变值之后，对原始电压数据进行移相处理，移相后的电压数据可以快速计算出电压暂降深度。较之传统的空间矢量法检测电压暂降需要采集一个电压周期内的三相电压数据，此方法所需数据量小、算法运行时间更短。仿真实验取得了较好的结果，证明此方法具有一定的实用价值。