交流电弧炉供电网波动电压超短期混沌预测方法*

王育飞，孙路，张剑云，薛花

（1.上海电力学院电气工程学院，上海200090；2.国网义乌供电公司工程管理部，浙江义乌322000）

0 引 言

交流电弧炉作为电力系统中典型的冲击性负荷，对供电网的电能质量具有重大影响，其中电压波动问题最为显著、也最难以克服［1］。国内外对电弧炉引起的供电网电压波动问题进行了大量的研究，主要集中在电弧炉模型的建立［2-3］和电压波动的抑制两个方面［4-8］。模型研究大多将电弧炉作为一个随机负载，根据实际电弧的物理机理建立微分方程数学模型来模拟电压波动。但由于电弧的变化具有高度非线性和强随机性，建立精确、实用的电弧炉数学模型非常困难，而目前的研究也反映了这一点。电压波动抑制措施研究主要通过在电弧炉供电网侧加装无功功率补偿装置来降低电压波动的水平。目前工程上多采用SVC就近补偿无功来抑制电压波动，但SVC内部晶闸管的开通和关断存在触发延迟［9］，致使无功实际补偿时刻与预补偿时刻不一致，实时补偿能力有限，电压波动抑制效果很难得到进一步提高。

事实上，电弧炉系统是一个十分复杂的系统，供电网电压波动受众多因素影响，因此通过建立精确的电弧炉数学模型不太现实。而混沌理论可以对表面貌似随机、无序的现象进行分析建模，已在各领域复杂对象的分析研究中得到了应用［10-14］。电弧弧长的变化虽然表现出随机性，但电弧位于整个电弧炉系统的末端，这种随机性未必能够在系统首端即供电网侧得到保持，因为同一供电网往往连接着其它负载，它们对供电网的电压也存在一定的影响。因此可以利用混沌理论对电弧炉供电网波动电压进行分析研究，同时利用该理论的预测功能对电压进行预测，若能与SVC有效结合，将大大提高电压波动的抑制效果。目前国内外利用混沌理论对电弧炉系统参数进行研究的文献较少，且都局限于对靠近电弧炉末端的参数研究，未考虑供电网侧参数的变化，而供电网电压正是电力工作者极为关注的对象，它关系到电力系统的全局稳定性。

基于某炼钢厂采集得到的电弧炉供电网电压有效值时间序列，首先，通过相空间重构技术建立电压时间序列的分析模型和计算时间序列最大Lyapunov指数，从定性和定量两方面确定系统混沌特性；然后，分别采用最大Lyapunov指数预测法和加权一阶局域预测法对电压进行超短期预测并作对比分析。结果表明，两种方法都能够很好地预测系统的超短期变化趋势，而加权一阶局域预测法相较于最大Lyapunov指数预测法能在更宽的时间范围内对电压进行较准确的预测。通过混沌预测，提前掌握电弧炉供电网的超短期电压变化情况，对于结合SVC有效提高电压波动的抑制水平，保证供电网及电力系统的安全稳定具有重要的实际意义。

1 电弧炉供电网电压的测量

选取某炼钢厂交流电弧炉供电系统作为电压检测对象，如图1所示。其中，T1为工厂用电配电变压器，T2为电弧炉供电系统变压器。通过安装在变压器T1二次侧的电压互感器测量33 kV母线上某相相电压的有效值。电弧炉在熔化期电压波动最为剧烈，因此电压测量时间设置在熔化期。由于目前SVC的响应时间已达到毫秒级，理想状态下为20 ms左右［15］，故设定电压有效值采样时间为Δt=0.02 s，即一个工频周期。图2是测量得到的电弧炉系统相电压有效值时间序列数据，在60 s内共3 000个数据。

如图2所示，相电压有效值在基准值18.95 kV附近波动，波动幅值为100 V左右，各点波动幅值之间无明显规律。相对于基 准值，电压波动幅值不是很大，这是因为炼钢厂已用SVC对无功作了补偿，使得电压波动程度大大下降了。但这100 V的波动对于同一供电网中的其它负载仍存在危害，因此进一步降低电压波动仍十分必要。

图1 交流电弧炉供电系统Fig.1 Power supply system of AC EAF

图2 电压有效值测量数据Fig.2 Measured data of voltage value

2 电压时间序列混沌特性分析

2.1 相空间重构参数的确定

系统的相空间重构可以将表面看似复杂且毫无规律的时间序列从一维扩展到多维，恢复系统的混沌吸引子，以此提取系统内部蕴含的规律和丰富信息。将图2所示的电压有效值数据组成时间序列，记为 u（ti），i=1，2，…，N（N为序列长度），重构相空间如式（1）。

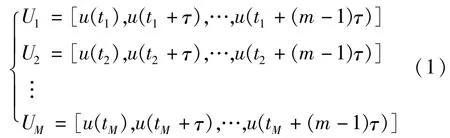
其中，τ=lΔt（l=1，2，…）为延迟时间；m为嵌入维数；U（k）（k=1，2，…，M）为延迟向量，亦即相空间中的点；M=N-（m-1）l为相点的个数。

互信息法从概率的角度对时间序列的延迟时间进行确定，实际计算时，考虑到延迟时间τ是采样时间Δt的倍数，即τ=lΔt，取互信息函数为l的函数，并定义l为延迟量。基于互信息法确定系统电压时间序列最佳延迟量确定如图3所示。

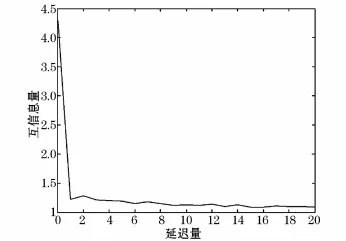
图3 电弧炉系统电压时间序列互信息量曲线Fig.3 Mutual information curve of EAF voltage time series

电压时间序列互信息量在开始阶段随着延迟量的增大迅速下降，在延迟量l=1时出现第一个局部极小值点，确定为系统的最优延迟量，最优延迟时间τ=0.02 s。

基于Cao氏法在伪最近邻域法中阈值选择上的优势，采用Cao氏法确定电压时间序列最优嵌入维数。基于互信息法确定的最优延迟量，引入E1（m）和E2（m）两个变量作为最优嵌入维数选择标准，当E2（m）不始终为1且E1（m）随 m的增加达到饱和时，确定系统最优嵌入维数为m+1。采用Cao氏法确定电弧炉电压时间序列最佳嵌入维数如图4所示。

从图4中可以看出，嵌入维数m从1增加到16，E2（m）的值始终在数值1附近波动，而E1（m）的值逐渐增大并趋向于1值而达到饱和。当嵌入维数增加到6维时，E1（m）的值增长速度变缓，达到饱和状态。可确定电弧炉电压时间序列最优嵌入维数m=7。

图4 嵌入维数变化曲线Fig.4 Changing curve of embedding dimension variation

利用确定的m和l重构相空间，得到电弧炉电压时间序列二维相图如图5所示。二维相图曲线具有自相似轨迹，且呈现出双涡卷结构，与Lorenz混沌吸引子图对比分析，可定性判断出电弧炉电压时间序列具有混沌特性。由于测得的电压时间序列数据中大量的噪声信号影响，在一定程度上破坏了相空间轨迹中相邻相点之间原有的相关性，使得相点的演化发生错位。因此与平滑的Lorenz系统混沌吸引子轨迹相比，电压时间序列相图中系统空间轨迹呈现出许多的毛刺和凸起。

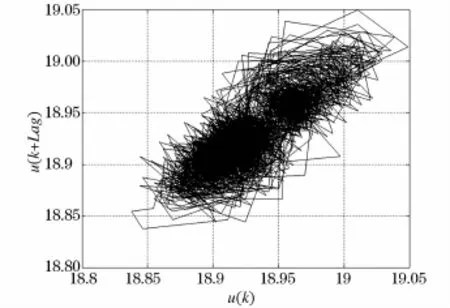
图5 电压时间序列二维相图Fig.5 Two-dimension phase diagram of voltage time series

2.2 最大Lyapunov指数的提取

为了更加直观的判断电弧炉电压时间序列的混沌特性，选取最大Lyapunov指数对系统特性进行定量判断。采用小数据量法求取指数值如图6所示。

图6 计算最大Lyapunov指数的y（k）-k曲线图Fig.6 The y（k）-k curve for maximum Lyapunov exponent computing

图6中，红线为用最小二乘法拟合的曲线y（k）-k的平均线，其斜率即为电压时间序列最大Lyapunov指数。图6中红线的斜率为0.022 1，指数值大于零，说明电压时间序列演化轨迹呈现出发散形态，定量判断出电弧炉供电网电压时间序列存在混沌特性。

基于电弧炉供电网电压时间序列特性的定性和定量判断，确定系统混沌特性。混沌系统的短期行为具有一定的确定性，因此电弧炉供电网电压波动预测具有可行性。

3 电压时间序列混沌预测

为简便起见，不考虑采样时间，将电压有效值时间序列记为 u（1），u（2），…，u（N），保持重构参数不变，则重构相空间变为式（2）：

其中 u（M+（m-1）l）即为 u（N）。下面用两种不同的方法对电压有效值时间序列进行预测。

3.1 基于最大Lyapunov指数的电压预测

设λ1为电压有效值时间序列的最大Lyapunov指数，选取UM为重构相空间中的预测中心点，寻找UM最近邻域点UK，两者之间的欧氏距离为dM（0），有：

其中Uj对应UM的邻近点，UM和UK经一步演化，即经过一个采样时间后分别成为UM+1和UK+1，根据最大Lyapunov指数的定义，有：

式中对应的未知参量只有UM+1中的最后一个分量为 UM+1，m，对应为 u（M+1+（m-1）l）=u（N+1）为预测值，有：

其中：

式（5）中，正负号的选取可通过判断相空间中两矢量之间的夹角确定。当两向量之间的夹角较小时说明两空间矢量越接近［16］，可通过以下方式判断：

假设空间中的两个矢量为：

V=（x1，x2，…，xm），W=（y1，y2…，ym）

它们之间的夹角为：

记取“+”号时的电压有效值预测值为ui+，取“-”号时的电压有效值预测值为ui-，u+=（ui+，ui-1，…，ui-n），u-=（ui-，ui-1，…，ui-n），u'=（uj，uj-1，…，uj-n），j=i-1，再分别计算 u+与 u'、u-与 u'的夹角，分别记为 θ+、θ-。若 θ+＜θ-，式（5）取“+”；反之，取“-”。

3.2 考虑邻域点位置影响的电压预测

首先确定预测中心点UM的若干个邻域点，设定一极小的正数ε作为欧氏距离，若UM周围的点满足：

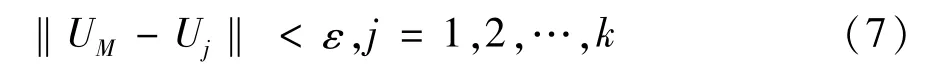
则确定了UM的k（k为整数）个邻域点Uj。根据相空间轨迹，确定邻域点Uj的下一演化点Uj+1，寻找Uj和Uj+1之间的关系，使得：

其中，A、B为拟合参数，为待求值：

A=［a1，a2，…，am］T

在 Uj+1中，仅最后一个分量 uj+1+（m-1）l为未知量，亦即预测量，有：

事实上，不同的邻域点对预测中心点的演化影响不同，其中离预测中心点越近的邻域点对预测结果的影响越大。为此，在式（8）中引入一权值Wi（i=1，2，…k）如下：

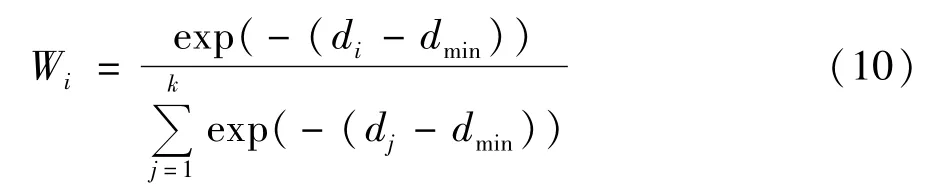
其中，di为选取的预测中心点与对应的第i个邻域点Ui之间的空间距离；dmin为所有距离中的最小值。参照式（8），有：

求出式（12）中的参数，则预测点为：

3.3 预测结果及分析

以图2中包含3 000个电压有效值的时间序列重构相空间，重构参数以及最大Lyapunov指数参照上文所得结果，采用以上两种预测方法对从第3 001个点开始的后60个数据点进行预测，并将这60个点分成前后三组，每组20个。图7给出了两种方法的预测值与实测值的对比结果。

图7（a）为前20个点 （第3 001～第3 020数据点）的预测结果。两种方法的预测值与实测值均比较接近，能动态跟踪电压的变化。其中，基于最大Lyapunov指数预测法（简称方法一）的平均相对误差为0.053%，加权一阶局域预测法（简称方法二）的平均相对误差为0.033%，说明方法二的预测精度比方法一要高。图7（b）为中间20个点（第3 021～3 040数据点）的预测结果。方法一的平均相对误差为0.062%，方法二的平均相对误差为0.041%，与图7（a）类似，但两种方法的误差均有所增加。图7（c）为后20个点（第3 041～3 060数据点）的预测结果。方法一和方法二的相对误差分别为0.106%和0.065%，亦较图7（b）有所增长。由此可见，方法一和方法二均能在较短时间内反映电压有效值的变化趋势，且相对误差很小。随着预测长度的增加，相对误差逐渐增大，但方法一比方法增加得快，说明随着误差的逐渐累积，方法一最终将先于方法二超出误差允许范围，即可预测范围。这可以从两种方法的预测原理上加以解释。方法一以最大Lyapunov指数建立电压有效值预测模型，而最大Lyapunov指数表示的是整个相空间轨迹的平均发散程度，因此式（2）仅仅是对相空间轨迹演化真实规律的近似，用轨迹平均发散率代替动态变化的发散率必然导致预测误差的逐渐积累，而且累积速度可能加快。方法二由于考虑了邻域点位置对预测中心点的影响，通过邻域点的演化跟踪预测中心点的演化，从而建立两者之间的紧密联系，预测误差增长较为平缓，因此该方法更适合作为电压有效值时间序列的预测方法。

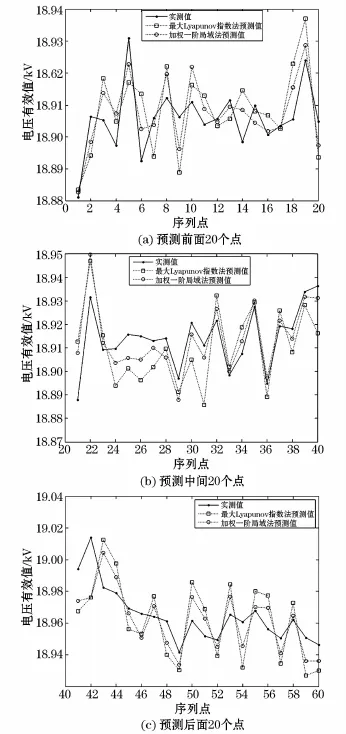
图7 两种方法的电压有效值预测结果Fig.7 Voltage prediction result of the two methods

4 结束语

提出用混沌理论对交流电弧炉供电网电压有效值时间序列进行特性分析并做超短期预测。通过现场测量得到电压有效值时间序列，采用互信息法和Cao氏法分别确定最佳的延迟时间和嵌入维数并重构相空间；绘制二维相空间图，并计算最大Lyapunov指数。结果表明电压波动具有混沌特性，可以用混沌的方法对电压进行预测。

分别采用基于最大Lyapunov指数法和加权一阶局域预测法对电压时间序列进行超短期预测，结果表明，混沌预测能够较好地反映交流电弧炉供电网电压有效值时间序列的变化趋势，超短期预测精度高，且加权一阶局域预测法比最大Lyapunov指数法的预测精度更高，适合作为电压有效值时间序列的预测方法。